Решение проблемы СВЧ-нагрева композиционных материалов

Многообразие геометрических размеров и форм обрабатываемых диэлектриков, различие их электрофизических параметров затрудняет создание универсальных СВЧ-камер для обработки диэлектриков, систем многоэлементного возбуждения электромагнитного поля с рациональной структурой и параметрами [1].

Процессы нагрева в СВЧ-камерах описываются системой нелинейных дифференциальных уравнений в частных производных, состоящей из уравнений Максвелла и, в отсутствии массо-переноса, уравнения теплопроводности [2]. Исследование подобных систем дифференциальных уравнений сопряжено с большими трудностями не только вычислительного, но и принципиального характера [2].

Во многих технологических процессах электромагнитное поле воздействует на диэлектрик, находящийся в металлической оболочке цилиндрической формы [3].

В данной работе исследуются задачи формирования и оптимизации электромагнитных и температурных полей в цилиндрических областях.

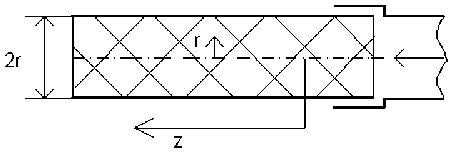
Рис. 1. Электродинамическая модель

1. Формирование и оптимизация электромагнитных полей

Во многих технологических процессах СВЧ-нагрева и плавления диэлектрика требуется обеспечить равномерный нагрев в объеме обрабатываемого материала. Учитывая низкую теплопроводность многих диэлектриков и короткое время обработки, можно считать это требование равносильным требованию создания ЭМП с равномерным распределением модуля напряженности электрического поля.

Приемлемой моделью для анализа может служить представление цилиндрического объема в виде короткозамкнутого круглого волновода с однородным заполнением (рис. 1). Для повышения равномерности распределения ЭМП в заданном объеме может быть использован как выбор типа волны и ее параметров, так и многомодовое возбуждение со специально подобранными составом и амплитудами типов волн.

В любом из вариантов возбуждения параметры, влияющие на процесс формирования ЭМП в заполненной части волновода, выбираются из условия равномерности модуля напряженности электрического поля. В качестве критерия, в зависимости от конкретного типа технологического процесса, могут выбираться как минимаксные

@ 1 = min | Ё ( r , ф , z )| , (1)

V

@ 2 =

min | E ( r , ф , z )|

V

max | E ( r , ф , z )|

V

представляют моды с наибольшими значениями критической длины волны E ₀₁ и H ₁₁.

Выражение для интенсивности поля можно

так и интегральные критерии

@ 3

= J const - | E ( r , ф , z )|

V

dv ,

где V – объем обрабатываемого материала.

Задача оптимизации возбуждения состоит в определении управляющих параметров x , при которых обеспечивается максимальное значение критериев @ 1 и @ 2 , или минимальное для критерия @ 3 . Конкретный вид выражения для |E ( r , ф , z )| и параметров | X определяется способом возбуждения. Далее рассматривается ряд вариантов осуществления оптимизации возбуждения.

представить в виде

2п f                 2

I E E ( r , z )² = j j E m _n ( r , ф , z )| x

0 ¹

^x |exp( -Y mn ^z ) ^{- ex} P ^{( -}Y mn ⁽² L ^{- z ))}2 +           (4)

+ |Emn(r, ф> z )|2 x x |exp(-Ym„z) + exp(-ym„ (2L - z))|2 j dф, где Emn (r, ф, z), Emn (r, ф, z) — поперечные и продольные составляющие напряженности электрического поля волн mn-типа; уmn — постоянная распространения; L – длина заполненной части

2. Одномодовое возбуждение

В простейшем случае в рассматриваемом волноводе возбуждается единственный тип волны.

волновода.

Для волн электрического и магнитного типа указанные составляющие имеют вид:

для волны E q1 поперечная составляющая —

Г

Варьируемыми параметрами являются тип волны и частота колебаний. Исходя из требования равномерности распределения | E ( r , ф , z )| , должны использоваться либо моды с нулевой ази-

E r ( r , z ) = - j 4-. 1 —

^X kp

f X

l^X kp J

мутальной зависимостью – E_оп , H_оп , либо пар-

I                     r I x I -^1(П01— I exp( - jhz),

I          ^r 0 J

ные моды, временной

возбуждаемые в пространственной и квадратуре, например H ^x ) ± jH ^y ) .

В любом случае при анализе можно ограни- читься исследованием двумерных распределе- ний, усредненных по азимутальной координате E(r, z) . Наибольший практический интерес

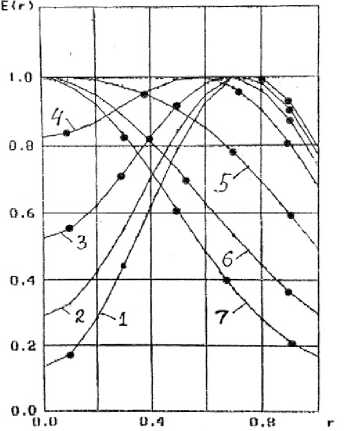
Рис. 2. Зависимости модуля напряженности электрического поля для волны E01 от радиуса при разных значениях X / Tq продольная составляющая –

Ez(r, z) = Jo(no1 — )exp( - jhz),(6)

r ₀

для волны H ₁₁ поперечные составляющие –

E— (—, z) = j—Zb--kp J1(Ц11 — )exp( - jhz),(7)

Ш1 r— X r0

Eф(r, z) = jZb -kp J1(Цц — )exp( - jhz),(8)

X где Xkp = 2nTq / П01 для волны Eq1 и Xkp = 2п — / Цц для волны Иц, а Zb = zj ц a / б a — волновое сопро-

Таблица 1

X / r 0	ор.онач.	@ 3
0,5500000	0,6444284	0,2428160
0,8000000	0,7046255	0,1287258
1,0500000	0,7923860	0,0431070
1,3000000	0,8870471	0,0111597
1,5500000	0,8389985	0,0400984
1,8000000	0,6941408	0,1236596
2,0500000	0,5989680	0,2488346

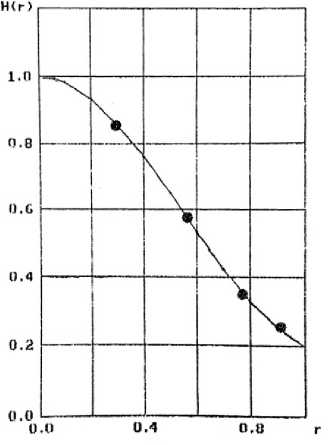
Рис. 3. Зависимости модуля напряженности электрического поля для волны H ₁₁ от радиуса при разных значениях λ / r ₀

тивление; J ₀( η ₀₁ ), J ₁( µ ₁₁ ^r ) – функции Бес- r ₀ r ₀

селя.

В случае одномодового возбуждения варьируемыми величинами являются отношение λ / r ₀ и тип волны. Проведены расчеты модуля напряженности электрического поля для волны E ₀₁ и для волны H ₁₁ в сечении волновода z = 0 в зависимости от радиуса r (0 ≤ r ≤ r ₀) для типичных значений параметров заполнения ε= 2, tg δ = 0.05, при этом варьируемым параметром являлось отношение λ / r ₀ .

На рис. 2 приведены зависимости модуля напряженности электрического поля для волны E ₀₁ от радиуса при разных значениях λ / r ₀ , которые приведены в первом столбце таблицы, расположенной справа от рисунка (кривые пронумерованы в порядке возрастания значения λ / r ₀).

В табл. 1 приведены значения критерия Θ ₃. Приведенные результаты расчетов показывают, что за счет изменения значения λ / r ₀ (что Таблица 3

Таблица 2

λ /r0 ор.онач. Θ3 0,5500000 0,6293924 0,2048126 0,8000000 0,6293924 0,2048126 1,0500000 0,6293924 0,2048126 1,3000000 0,6293924 0,2048126 1,5500000 0,6293924 0,2048126 1,8000000 0,6293924 0,2048126 2,0500000 0,6293924 0,2048126 равносильно изменению частоты возбуждения) можно добиться существенного снижения значения критерия Θ3 .

На рис. 3 приведены аналогичные зависимости модуля напряженности электрического поля для волны H ₁₁. Проведенные расчеты показывают, что значение модуля напряженности электрического поля для волны H ₁₁ не зависит от величины отношения λ / r ₀ . Значения λ / r ₀ и значения критерия Θ ₃ приведены в табл. 2

Проведены расчеты модуля напряженности электрического поля для волны E ₀₁ и для волны H ₁₁ в зависимости от радиуса r (0 ≤ r ≤ r ₀) и z (0 ≤ z ≤ L ), при этом варьируемым параметром также являлось отношение λ / r ₀ .

В табл. 3 приведены значения критерия Θ ₃ для волн E ₀₁ и H ₁₁.

Очевидно, что за счет изменения значения λ / r ₀ (что равносильно изменению частоты возбуждения) можно добиться существенного снижения значения критерия Θ ₃ во всем объеме обрабатываемого материала. Так, например, для волны E ₀₁ значение критерия Θ ₃ улучшается на 40 %, а для волны H ₁₁ – на 21 %.

• 3.    Многомодовое возбуждение

В рассматриваемом случае возможно осуществление как когерентного, так и некогерент-

λ / r 0	Θ 3 для волны E 01	Θ 3 для волны H 11	Θ 3 для E 01 + H 11
0,55	0,08	0,084	0,074
0,8	0,072	0,088	0,068
1,05	0,063	0,093	0,056
1,3	0,073	0,083	0,06
1,55	0,064	0,074	0,054
1,8	0,048	0,081	0,043
2,05	0,06	0,083	0,057

ного типа возбуждения [3]. При когерентном возбуждении

|E ( r , z )|2

MN

' '^ ' U mn E mn ⁽ r , z )

mn

где U_mn – амплитуда падающей волны mn -типа; *

E_mn ( r , z ) – распределение поля указанной моды.

Реализация когерентного возбуждения за- ключается в одновременном возбуждении требуемых мод с амплитудами Um генератором фиксированной частоты при помощи некоторого устройства возбуждения. Поскольку в общем случае при возбуждении волны некоторого типа происходит возбуждение волн ряда других ти- пов, то при оптимизации следует учитывать взаимную зависимость амплитуд Umn:

| Umn ) = [ B ]| U 0 ,

где U ₀ – вектор значений параметров возбудителя; [ B ] - прямоугольная матрица, зависящая от структуры возбудителя, электрических размеров волновода и частоты.

При некогерентном возбуждении:

|E ( r , z )|2 = " \^U mn ² | E mn ⁽ r , z f,            ⁽¹¹⁾

mn

Осуществить некогерентное возбуждение можно различными путями. Во-первых, возможно последовательное во времени возбуждение волн различных типов, во-вторых – возбуждение одного или различных типов волн с различными частотами.

Достоинством когерентного возбуждения является то, что оно несколько проще в реализации, недостаток – принципиально худшие показатели равномерности распределения поля в осевом направлении. В любом из случаев использование многомодового возбуждения позволяет улучшить показатели равномерности по сравнению с одномодовым возбуждением.

В качестве иллюстрации приведем пример, показывающий возможность улучшения показателя равномерности при некогерентном возбуждении волны E ₀₁ и волны H ₁₁, в котором варьируемым параметром также являлось отношение X / r Q . В табл. 3 приведены значения критерия @ 3 при некогерентном возбуждении волны E 01 и волны H ₁₁. Как показывают расчеты, значение критерия @ 3 уменьшается по сравнению с наилучшим значением, соответствующим одномодовому возбуждению, на 5 % при X / Г д = 2,05 и на 18 % при X / Г д = 1, 3.

Указанный выигрыш разумеется не является предельным при многомодовом возбуждении. Определение наилучшего способа возбуждения, числа и параметров возбуждаемых мод требует проведения детальных исследований для каждого технологического процесса.

Заключение

В последние годы активно проводятся исследования по применению СВЧ электромагнитного излучения при добыче и транспортировке нефти [3]. Наиболее распространенным способом транспортировки высоковязких нефтей и нефтепродуктов по трубопроводам является перекачка с подогревом.

В данной работе построена и исследована математическая модель СВЧ-нагрева движущейся жидкости в цилиндрическом трубопроводе, отличающаяся от математической модели исследованной в [3] тем, что в данном случае учитывается изменение температуры не только за счет конвекции, но и за счет механизма теплопроводности.

Приемлемой моделью для исследования СВЧ-нагрева жидкости в трубопроводе может служить представление трубопровода в виде цилиндрического волновода, в котором возбуждается один или несколько типов волн.

При построении математической модели предполагается, что поперечная составляющая скорости нефти равна нулю, а продольная составляющая скорости при ламинарном течении нефти в трубопроводе (число Рейнольдса < 2000) не изменяется по длине трубы и имеет параболическую зависимость от радиуса [4].

Работа выполнена при финансовой поддержке Министерства образования и науки Российской Федерации в рамках проектной части Государственного задания 3.1962.2014/К.