Решение системы уравнений марковского восстановления с помощью аппроксимации асимптотических рядов

Приближенные решения, построенные с помощью предложенного метода, сохраняют важные характеристики случайного процесса: заданное число первых моментов и производных в нуле точного решения. Моменты и производные соответствуют членам ряда асимптотического разложения точного решения в пространстве образов Лапласа в нуле и на бесконечности.

Метод восстановления состоит в построении двухточечной аппроксимации Паде образа Лапласа по двум асимптотическим рядам и добавлении дополнительных свободных параметров, используя свойства цепных М -дробей. Введенные таким образом параметры не изменяют заданное заранее число коэффициентов разложения и, варьируя их значение, можно добиться ограниченности и неотрицательности построенного приближения. Такие приближения соответствуют плотностям функций распределения.

Рассмотрим постановку задачи марковского восстановления с точки зрения применения данных уравнений для анализа безопасности ОПО (опасных производственных объектов). По теме полумарковских процессов смотри [1, 2, 3].

Рассматривается система S , способная находиться в N состояниях. Эволюция данной системы со временем является случайным процессом, который характеризуется вектором-столбцом Р ( t ) вероятности нахождения системы в каждом из N своих состояний для произвольного момента времени t >  0 .

Р ( t ) = ( P i ( t ) ,...,P n ( t)f , 0 <  t< го,

N

^ P i ( t ) = 1 , V t >  0 .

i=1

В начальный момент времени t o = 0 система имеет определённое (заданное) распределение вероятностей Р о = Р (0) нахождения системы в каждом из N состояний.

Характеристика переходов между состояниями задается следующим образом.

Выбор направления перехода из состояния с номером г в состояние с номером j осуществляется через величину тг^- — вероятность выбора пути перехода.

N

0 6 Tv_ij 6 1 Vi,j,    ^ тг^ = 1 ,    1 6 г 6 N.                       (2)

j=1

После выбора пути перехода из г в j с вероятностью 7r ij сам переход осуществляется через случайное время T ij . Данное время имеет функцию распределения G ij ( t ) с плотностью ^g ij ^{( t )} .

0 6 G ij ( t ) 6 1 , V t >  0 , V 1 6 г,j 6 N, ' g ij ( t ) = ^dG ^_t^{( t )} >  0 , V t >  0 , V 1 6 г,j 6 N.

Теперь определим уравнения марковского восстановления.

• 2.1.    Вид уравнений марковского восстановления

Система уравнений марковского восстановления имеет следующий вид:

t

V ( t ) = Ф ( t ) + j Q ( t ) • V ( t - t ) • dT,

V (0) = I .

Функциональная матрица V ( t ) называется матрицей условных вероятностей перехода. Функциональная матрица Q ( t ) - плотность полумарковского ядра. Ф ( t ) — диагональная функциональная матрица, I - единичная матрица. Все матрицы имеют размер N х N .

Уравнения на вероятность Р ( t ) для системы S имеет следующий вид:

Р ^Т ( t ) = Р Т • V ( t ) , t >  0 .                                 (5)

Связь уравнений (4) и (5) через свойства переходов системы имеет следующий вид:

Q (t) = ^ х g (t),   0 6 t < то, dij (t) := (Q (t))^^ = -ij • дц (t), V1 6 i,j 6 N, (Ф (t))ij = 5ij • (1 - £ -k • Gik (t)) , V1 6 i, 3 6 N,

где 6 ij - дельта-символ Кронекера. В дальнейшем будет удобнее работать не с вероятностью Р ( t ) , а с ее плотностью / ( t ) , поэтому, продифференцировав уравнение (5) по t, получим уравнение на плотность.

/ ( t ) := Р ^Т ( t )= P Т • K ( t ) := Р Т • U ( t ) ,

U ( t ) = Ф ( t ) + Q ( t ) +

t

J Q ( т ) • U ( t — т ) • dr. 0

В дальнейшем решаем уравнение (7), где U ( t ) = V ( t ) . Нашей конечной целью будет поиск приближенного решения / ( t ) для любого момента времени t >  0 , которое бы имело важные свойства, описанные ниже (сохранение заданного числа первых моментов и первых производных в нуле).

• 2.2.    Система уравнений марковского восстановления в пространстве образов Лапласа

Как известно, линейные уравнения сверточного типа (4) и (7) в образах Лапласа имеют более простой вид, в котором свертка переходит в произведение:

/ * ( з )= Р Т • U * ( 5 ) ,

( I — Q * ( 5 )) • U * ( 5 ) = ( Ф * ( 5 ) + Q * ( s ) ).

Второе уравнение из формулы (8) имеет следующий эквивалентный вид:

А ( 5 ) • Х ( 5 ) = В ( 5 ) ,

^{( А ( 5 ))} ij = ⁵ ij ^{— -} ij • д * ^{( 5 )} ,

^{( В ( 5 ))} ij = ⁵ ij •

/ N

—Е

\ к=1

^- ik • g ik ^{( 5 )}

)

^{+ -} ij • g *j ^{( 5 )} ,

• 2.3.    Важные характеристики случайного процесса

Для случайного процесса, описываемого набором состояний и переходов с функциями распределения (5), его важными характеристиками являются моменты (математические ожидания) и поведение вблизи нуля ( t ^ 0) , так как отражают существенные статистические характеристики.

Математическое ожидание плотности f ( t ) функции распределения определяется как

∞ тк

I t ^k • f ( t ) • dt, к = 0 , 1 , 2 , ..., о

где считаем, что плотность имеет моменты любого порядка.

За поведение при t ^ 0 отвечают производные плотности в нуле:

f(к-1) (0) := d f (t)     , к = 1, 2, 3, ..., k—1

^dt       t=0

где считаем, что плотность имеет ограниченные производные любого порядка.

Если над плотностью f ( t ) функции распределения Р ( t ) проделать преобразование Лапласа, то образ будет иметь следующие свойства [4]:

∞ f * (s) = ^^ ск • sk,   s ^ 0, ск = (—1)fc • “кр,   к = 0, 1, 2, ..., к=0

∞

f * ( s ) = Е ' , s ^~ ,  с - _к = f (k^-1 (0) , к = 1 , 2 , 3 , ...

к=1 ^S

Из уравнения (12) видно, что коэффициенты разложения образа Лапласа в нуле и на бесконечности для плотности функции распределения как раз и содержат важные статистические характеристики. На практике можно найти только конечное число разложений вида (12) для уравнений (8) или (9). Далее будем считать, что нам удастся найти первые М членов разложения.

• 3.    Рекуррентные уравнения для членов асимптотических рядов решения системы уравнений марковского восстановления

Для получения рекуррентных соотношений на члены асимптотических рядов, которые являются решением (9), перепишем матричное уравнение (9) двумя способами:

A ( s ) • X ( s ) = В ( s ) , X ( s ) = A ^{- 1} ( s ) • В ( s ) .

Разлагая каждую из матриц первого уравнения в формуле (13) по прямым и обратным степеням s, получим следующие рекуррентные соотношения для асимптотического разложения точного решения:

X 0^о] = ,.! ■ '•„ 0^0] ,

X 0^1] = ,А • ,.-      A 0^ X 0^0] ),

...

X 0‘1 = (а00')-17в0‘1-е A0‘-hx 0"'^ \      "=0             / при s ^ 0, где A0k] X0k] и B0k - коэффициент матричного разложения в нуле при sk, к = 0,1, 2,.... Для разложения по обратным степеням имеем:

X ^{[ - 1]} = (а Н ¹ • в^{[- 1]} о у^Ло о^ ,

X[-2] = (А[0П 1 • (В[-2] - А[-1] • Х[-1П о 1Ло І-^о -^о о у,

(15) ...

X 0^k] = ( а О ) ^{- 1} • ( в -1 - £ 4^ +“] • X 0“1 )

при s ^ то, где а О ^{/< ]} , X 0^k] и B 0 ^k — коэффициенты матричного разложения на беско-

нечности при s

^k — 1 /s ^k к — 1 , 2 , 3 ,.... а ОО — I для полумарковского процесса (в силу

поведения образов плотности на бесконечности не медленнее 1 /s).

Уравнения (14) и (15) верны, если в описываемой системе S есть хотя бы одно поглощающее состояние (состояние, из которого нет ни одного выхода). Такое решение называется

невырожденным (( а 0° )

– существует). Если в описываемой системе нет ни одного погло-

щающего состояния, то разложение (14) в нуле не имеет места и необходимо пользоваться вторым матричным уравнением из (13). Такой случай называется вырожденным , так как

для него не существует обратной матрицы ^А ₍00^1] J

. В ней содержится линейно-зависимая

строка. В данном случае применяется следующий способ получения разложения. Запишем в упрощенных обозначениях, где не надо указывать точку разложения – она ноль, другой вид разложения матрицы A ( s ) .

A ( s ) — A o + A 1 • s + A 2 • s ² + A 3 • s ³ + ... + A _n • s " + ...

A ¹ ( s ) — Y —1 • —+ Y 0 + Y 1 • s + Y 2 • s ² + ... + Y _n—1 • s^{n 1} + ... s

Используем следующие два условия для определения матриц Y k , к — — 1 , 0 , 1 , 2 ,...

A ¹ ( s ) • A ( s ) — I о ^Y- 1 • —+ Y 0 + Y 1 • s + ...^ • ( A 0 + A 1 • s + A 2 • s ² + ...) — I ,

X 0 + X 1 • s + X 2 • s ² + ...

— (y -1 • s + Y 0 + Y 1 • s + ...) • ( В 0 + В 1 • s + В 2 • s ² + ...).

Последовательно разрешая систему (17), можно также найти необходимое число коэффициентов разложения матрицы X ( s ) в нуле. При этом, в отличие от невырожденного случая, если мы хотим получить М членов разложения решения в нуле, то понадобится М + 2 коэффициентов разложения матрицы A ( s ) и М + 1 коэффициентов разложения матрицы В ( s ) . Для невырожденного случая нужно одинаковое число коэффициентов разложения. Отметим, что при желании определить по 10 точных моментов и производных решения указанным способом, то в 1 Gbyte памяти ЭВМ поместится порядка 10 ³ (тысячи) состояний. Таким образом, можно на практике находить разложения для достаточно больших систем.

• 4.    Метод восстановления по асимптотическим рядам

• 4.1.    Аппроксимация Паде по двум рядам

Ранее было показано, как получить конечное число моментов и производных в нуле точного решения системы уравнений полумарковского восстановления. При этом о функции распределения переходов требуется знать только их коэффициенты разложения по моментам и производным. Как результат, для каждого состояния г Е S имеем конечный набор действительных коэффициентов |с--]м, ..., с^_11, которые характеризуют данное состояние г. Конечной нашей целью будет построить функцию Pt (t) для 0 6 t < то и для всех состояний г системы S, которые бы сохраняли найденный набор коэффициентов разложения, были ограничены и являлись вероятностями (0 6 Pt (t) 6 1, Vг).

Всего может быть три типа состояний в системе: источниковые (есть только выходы из состояния), промежуточные (есть минимум один вход и один выход) и поглощающие (есть только входы в состояние). Для первого типа вероятность будет строго неотрицательной, невозрастающей и ограниченной, для второго типа вероятность будет неотрицательной и ограниченной и для третьего типа вероятность будет неотрицательной, ограниченной и неубывающей функцией. Основным признаком является ограниченность решения и, затем, его монотонность. Именно эти свойства необходимо получить и в приближенном решении, сохраняющем моменты с производными.

Дальнейшей целью решения является получение ограниченной и, если нужно, неотрицательной функции, при сохранении заданного числа ее первых моментов и производных в нуле. Поэтому можно отстраниться от способа получения коэффициентов разложения и акцентировать внимание на способе восстановления некоторой плотности по двум рядам.

Пусть плотность J ( t ) в пространстве образов Лапласа представлена только конечным числом коэффициентов С к разложения образа J * ( s ) в нуле и на бесконечности (знак минус выделен для дальнейшего упрощения) [5, 6].

J * ( s )

М -1

L o = Е с к • s ^k

к=0

М

L .

-

ү^ ^с - к

к=1

Построим аппроксимацию образа Лапласа в виде рациональной функции, имеющей М первых членов разложения из формулы (18). Причем, так как для функций распределения в общем случае затухание на бесконечности не быстрее 1 /s, то выберем рациональную функцию, степень числителя которой на единицу меньше степени знаменателя (поддиагональная аппроксимация Паде). Таким образом, строим функцию

[ М - 1 /м ] = ^Р М —1 ⁽S) ,   Q m (0) = 1 ,

Q m ( s )

где Р м —1 ( s ) и Q m ( s ) — полиномы степени М — 1 и М соответственно. Нумерация коэффициентов полинома происходит по возрастанию от коэффициента при старшей степени к свободному члену.

Для построения [ М — 1 /М ] через два ряда, записанного в виде (18), необходимо сначала определить коэффициенты знаменателя по формуле

с - М    с - М +1    с - М +2    • • •   с- 1		" 9 1"		с 0
с - М +1   с - М +2   C L - M +4   • • •   с 0		9 2		С 1
с - М +2 с - М +3 с - М +4    • • •    с 1 .                                 .                                   ..                          . .     .      .    ..	·	9 3 . .	=	С 2 . .	.                (20)
.                                         .                                            .                                       .. с -1        с 0          с 1       • • •   с М - 2_		. _ 9м_		. _ сМ -1_

Числитель можно определить по одному из рекуррентных соотношений:

М+1 - к                    к

Р к = 52 C t - 1 • 9 к+г ; — Р к = 52 9 г • С - к - 1+t , к = 1 , 2 ,...,М.

г=1                          г=1

Таким образом, построенная рациональная функция сохраняет М первых коэффициентов разложения формулы (18) в нуле и на бесконечности.

Однако редко рациональное приближение, построенное по формулам (20) и (21) с использованием коэффициентов рядов (18), будет являться образом Лапласа плотности распределения некоторой случайной величины. В построенном приближении могут возникнуть следующие проблемы:

• 1)    полюса рационального приближения могут находиться в области Re [ s ] >  0 , что приводит к неограниченному прообразу;

• 2)    прообраз рационального приближения не для всех t будет неотрицательной функцией, чего не должно быть для плотности функции распределения.

• 4.2.    Цепные М -дроби и их свойство

Обе эти ситуации являются широко распространёнными при практическом восстановлении. Первая проблема говорит о том, что прообраз является неограниченной функцией, а образ – неустойчивым.

В связи с обозначенными проблемами, необходимо найти способ такого изменения рационального приближения, при котором появлялась бы возможность сделать приближение устойчивым, а его прообраз неотрицательном на всей действительной полуоси по t, но сохранить разложения (18) для первых М членов обоих асимптотических рядов.

Цепная М -дробь имеет следующий вид (смотри подробнее [7, 8, 9, 10]):

∞ т (s)-r5i

(

s • F j

1 + G j • s

) -

F i

1 + G i • s +

sF

.•G 2- • i+ Q 3 ^F 3+

т (0)- F i , т ( s ^ro ) « ^F • - .

G i s

Особенность данного типа цепной дроби состоит в том, что:

• 1)    пара коэффициентов {F j , G j } определяется рекуррентно через предыдущие коэффициенты {F k , G k У - і и коэффициенты разложения вида (12) или (18), в которых используются значения C j - i и c -j .

• 2)    если определены первые М пар коэффициентов {F j , G j } j=i по первым М членам разложения функции в нуле и на бесконечности, то добавление нового внутреннего, глубинного звена с коэффициентами { F m +i ,G m +i } не изменит первых М членов разложений в асимптотические ряды, полученных ранее разложений.

Именно последнее свойство позволяет вводить в рациональную функцию новые пара- метры, при этом сохранять неизменными заданное число членов асимптотических рядов. Все коэффициенты Fj и Gj будут действительными числами, так как действительны коэффициенты Cj разложений, получаемых от любой действительной плотности.

Для построения нового частичного приближения необходимо знать только два предыдущих приближения и коэффициенты данного уровня цепной дроби [7, 8, 9, 10]. Обозначим М + 1 -ую частичную дробь как

Т м +i ( s|F, G ) -

Р м ( s|F, G ) Q m +i ( s|F, G ) ,

где Р м ( s|F, G ) - полином числителя степени М и Q m +i ( s|F, G ) - полином знаменателя степени М + 1 . F, G - свободные параметры дополнительного звена.

Полиномы числителя и знаменателя М + 1 частичной дроби выражаются через полиномы числителя и знаменателя М и М + 1 частичной дроби как:

Р м ( s|F, G ) :- (1 + s • G ) • Р м -i ( s ) + s -F • Р м -2 ( s ) , Q m +i ( s|F, G ) :- (1 + s • G ) • Qm ( s ) + s • F • Q m -i ( s ) .

Количество добавочных звеньев может быть произвольным. Но, так как функцию необходимо задать через явное значение её параметров, а на практике для большого числа звеньев это сделать затруднительно, то рассматривается простейший случай одного звена.

За счёт вариации параметров { F,G } , можно пытаться добиться необходимых свойств рациональной аппроксимации: устойчивости и вполне монотонности.

• 4.3.    Нахождение области устойчивости

Устойчивость рациональной функции определяется тем условием, что все её полюса имеют отрицательные действительные части. Таким образом, необходимо рассмотреть только корни знаменателя рационального приближения (24) [11].

Для полинома с действительными коэффициентами существует критерий Гурвица [11], который позволяет определить, все ли корни полинома имеют отрицательные действительные части. Такие полиномы называются полиномами Гурвица. Данный метод не требует нахождения корней полинома. Необходимо только собрать матрицу специального вида и, проведя прямой ход метода Гаусса, определить знаки диагональных коэффициентов. А именно, пусть есть полином

Q n ^{( s )} = q i • s ” + 7 2 • ^{s 1} + ... + q _n • s + q _n+i .                       (25)

Для него составим матрицу Гурвица размера п х п:
	7 2	7 4     • • •	0
Н п =	7 1 . . .	7 3 • • • .. .. ..	0 . . .	.                                       (26)
	0	0 •••	7 «+1_

Необходимо вычислить диагональные детерминанты матрицы Гурвица А^ г = 1 , ..., п. Если выполнено q i • A j >  0 , г = 1 , 2 ,..., п, то полином (25) является полиномом Гурвица (устойчив).

Полином знаменателя (24) имеет два свободных параметра. Зафиксируем связь между этими параметрами посредствам выбора действительного отрицательного полюса ( —А ) . Получим линейную связь между параметрами G и F :

G = ¹ - F • ^Q М -' ^:= ^ 0 + • F. (27)

^{А q} m ^{( —А )}

Полином Q m +1 ( s|F, G ) примет вид, зависящий от одного параметра. При выбранном значении А составим матрицу Гурвица для получившегося полинома, который зависит от одного свободного параметра F :

Н м +1 ^{( F} ) = Н м +1 ^{+ F} • Н м +1 . ⁽²8)

Для определения диапазона значений F , в которых полином устойчив, последовательно найдем все собственные значения матрицы Н М +1) • Н м +1 , вырезая в ней диагональные матрицы по аналогии с диагональными минорами. Получим ( М + 1) ( М + 2) / 2 собственных значений ^ j . Выберем из них только действительные. Внутри каждого интервала между действительными ^ j , вычислим критерий Гурвица для уравнения (28), полагая, например, F = — ( ^ j + ^+1 ) / 2 . Также проверим критерий Гурвица вне полученных интервалов действительных собственных значений. Те области, в которых выполнится критерий Гурвица, и будут соответствовать области Q ^ ( F ) устойчивости по параметру F при фиксированном значении полюса ( —А ) . Получающиеся области устойчивости будут односвязные (конечные или неограниченные) или их вообще не будет.

Варьируя параметр ( —А ) в диапазоне А >  0 , можно найти область устойчивости для всего диапазона изменения {F, G}.

• 4.4.    Определение неотрицательного прообраза

• 5.    Пример восстановления функции распределения

После того, как получена непустая область устойчивости Q a ( F ) , можно начинать процедуру приведения рационального приближения к виду, наиболее близкому к вполне монотонному. Для этого функция (24) разбивается на простые дроби и минимизируется вклад отрицательных амплитуд в рациональную функцию, путём варьирования значения параметра F в области устойчивости Q a ( F ) .

После того, как найдено значение F min G Q a ( F ) , при котором вклад отрицательных амплитуд минимален, применяется обратное преобразование Лапласа построенного приближения при фиксированном значении ( -А ) и F min . После этого непосредственной проверкой прообраза приближения необходимо убедиться, что он не принимает отрицательных значений на луче t >  0 . Если данное условие не выполняется, то необходимо выбрать новое значение параметра ( -А ) ив области устойчивости минимизировать свободный параметр F .

Описанные выше процедуры не гарантируют, что при добавлении одного звена в М -тую частичную дробь приближение I'm +1 ( s|F, G ) может быть приведено к требуемой форме. Если при заданном значении М числа точных моментов и производных вышеописанная процедура не приведёт к желаемому результату, то можно попробовать изменить количество членов ряда, которые сохраняются при разложении аппроксимации. Практика применения вышеописанного метода показывает, что данные случаи могут встречаться (одним звеном нельзя поправить данную пару приближения), но добавление одного нового точного звена и последующая процедура восстановления часто приводят к положительному результату.

Рассмотрим функцию распределения, на которой будут видны некоторые особенности восстановления функции по моментам и производным. Рассматриваемая точная функция имеет следующий вид:

f ( t ) =

1 . 3697811601597063

• { 2 • _е ^{- 1}^* + ( -е ^{- 1}^⁶ + е^-1'⁷⁴ - е^-^ + е ^-24 - е^²²⁴ + е ^{- 2}^ -

е ³" + е ^{- 3.И} - е ^{- 4.Ь6} + е ^{- 4.9}^ - е ^{-5/Л 6} ) • (1 + Cos [10 • t ]) }.

В функции (29) множитель перед скобками введен для нормировки функции на единицу. Первые десять коэффициентов разложения в ряд образа Лапласа f * ( s ) точной функции f ( t ) из (29) по степеням s имеет следующий вид (табл. 1):

Таблица1

Коэффициенты разложения образа Лапласа точной функции

Разложение при s ^ 0		Разложение при s ^ то
степень s	коэффициенты ряда	степень s	коэффициенты ряда
0	+1.00000000000000	-1	+0.00000000000000
1	-1.09102911482957	-2	+3.50420938731585
2	+1.12597279011802	-3	+4.77740546470726D+1
3	-1.16366860452755	-4	-5.86464483061292D+2
4	+1.20131528643162	-5	-2.57143557114293D+2
5	-1.23692946704608	-6	+5.01003892270326D+4
6	+1.26940434915159	-7	-5.82611250170230D+5
7	-1.29825385539188	-8	+4.66449145603942D+6
8	+1.32341955017117	-9	+1.03561335159912D+7
9	-1.34509124645834	-10	-1.17444299034570D+9

Образ Лапласа точной функции (29) имеет вид рациональной функции со степенью знаменателя, равной 34, степень числителя равна 33 и при s ³³ в числителе коэффициент равен нулю. В явном виде таблица коэффициентов точной рациональной функции не приводится. Минимальный по действительной части полюс точной рациональной функции является A min = - 1 . 00000000000000 , а точная амплитуда, соответствующая минимальному корню, имеет значение a min = 1 . 46008724471492 . Для построения приближений по моментам необходимо использовать максимальное число знаков арифметики, иначе происходит быстрое накопление ошибки в моментах и производных приближений с уменьшением числа точных знаков. Поэтому коэффициенты разложения представлены с 15-ю десятичными знаками точности.

Под символом aDb подразумевается a • 10 ^ь (запись для переменных двойной точности в Фортране).

Далее представлены результаты построения приближений различной степени для заданной функции распределения (29) по коэффициентам разложения из табл. 1. Графики строятся только для восстановленных функций распределения. Под порядком приближения будет пониматься количество точных первых моментов и первых производных, используемых при построении. Точнее смотри формулы (18) и (19). Для построенных приближений будет вычислена норма L i по определению

L i

=/

∞

| / ( t ) - / ^{[м 1} ( t ) |

• dt,

где / ^{[м 1} — приближение порядка М .

Приближение второго порядка . Образ Лапласа рационального приближения имеет вид [1 / 2] , построенный по набору коэффициентов { с - 2 , c - i , c g , c i }. Не потребовалось проводить восстановление через добавочные звенья. Норма L i = 0 . 36 . График прообразов смотри на рис. 1.

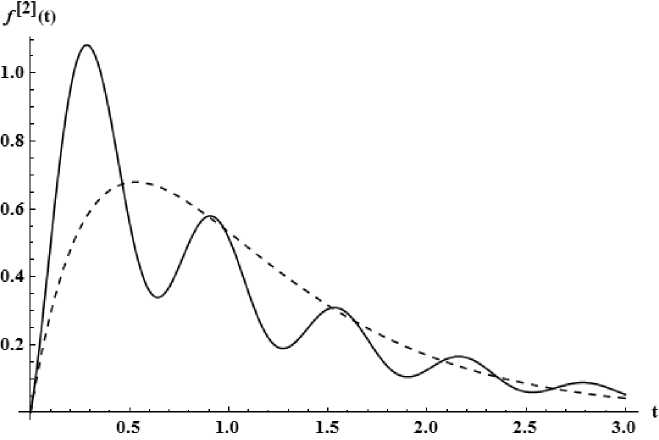
Рис. 1. Приближение второго порядка – пунктир, точная функция – сплошная линия

Приближение третьего порядка . Образ Лапласа рационального приближения имеет вид [2 / 3] , построенный по набору коэффициентов {с —з ,..., С 2 }. Не потребовалось проводить восстановление через добавочные звенья. Норма L i = 0 . 17 . График прообразов смотри на рис. 2.

Приближение четвертого порядка . Образ Лапласа рационального приближения имеет вид [3 / 4] , построенный по набору коэффициентов {с _-4 ,..., С 3 }. Не потребовалось проводить восстановление через добавочные звенья. Норма L i = 0 . 13 . График прообраза смотри на рис. 3.

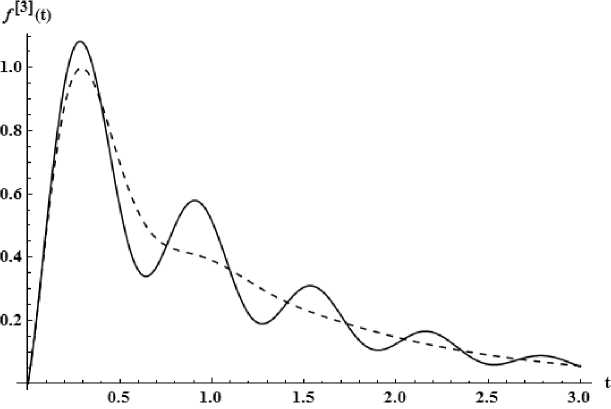
Рис. 2. Приближение третьего порядка – пунктир, точная функция – сплошная линия

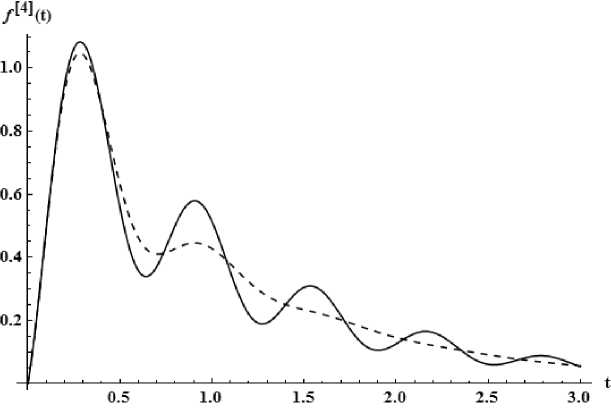
Рис. 3. Приближение четвертого порядка – пунктир, точная функция – сплошная линия

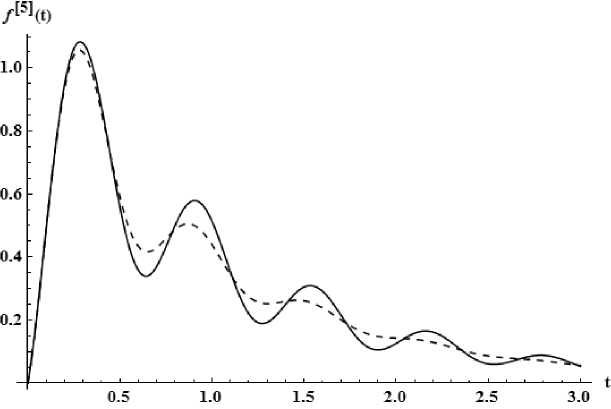
Приближение пятого порядка . Образ Лапласа рационального приближения имеет вид [5 / 6] , построенный по набору коэффициентов {с -5 , ..., С 4 } и одного звена Т -дроби. Потребовалось проводить восстановление. Восстановлено за одно звено Т -дроби при следующих значениях: A min = - 1 . 00000000000000 , F = 1 . 10869525793860 и G = - 0 . 254134631406592 . Норма L i = 9 . 7 х 10 ^{- 2} . График прообраза смотри на рис. 4.

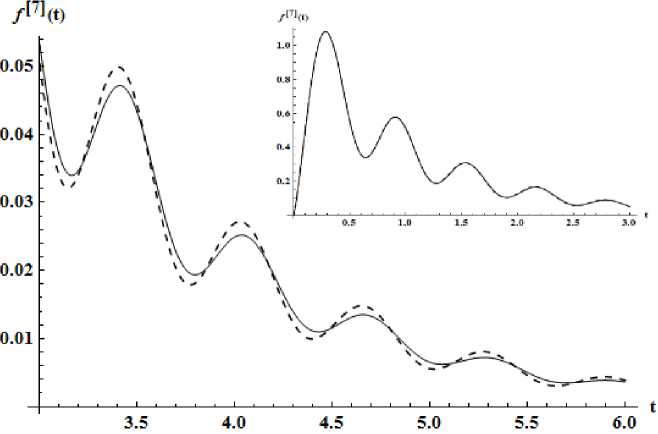
Рис. 5. Приближение седьмого порядка – пунктир, точная функция – сплошная линия

Приближение седьмого порядка . Образ Лапласа рационального приближения имеет вид [7 / 8] , построенный по набору коэффициентов { с - 7 , ..., С б } и одного звена Т -дроби. Потребовалось проводить восстановление. Восстановлено за одно звено Т -дроби при следующих значениях: A min = - 1 . 00000000000000 , F = 2 . 650801920933958 х 10 ^{- 2} и G = 0 . 376080793384200 . Норма L i = 8 . 9 х 10 ^{- 3} . График прообраза смотри на рис. 5. В правом верхнем углу представлен график сравнения точной функции с приближением на интервале t Е [0 , 3] . Визуально его трудно различить от точного, поэтому не указан подробно. Отличие хорошо видно на интервале t Е [3 , 6] , как представлено на рис. 5.

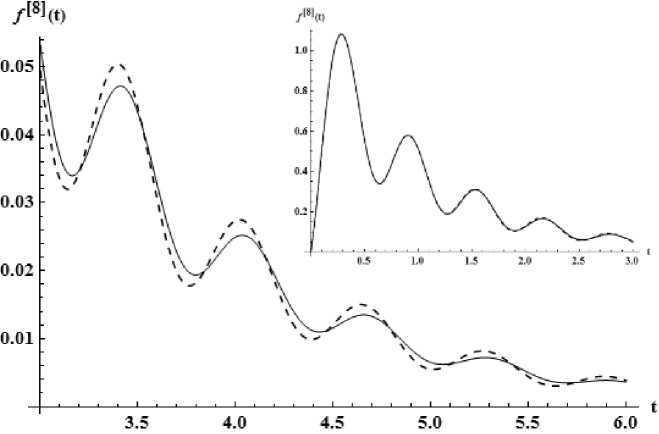
Рис. 6. Приближение восьмого порядка – пунктир, точная функция – сплошная линия

Приближение восьмого порядка . Образ Лапласа рационального приближения имеет вид [8 / 9] , построенный по набору коэффициентов {с -8 , ..., С 7 } и одного звена

Т -дроби. Потребовалось проводить восстановление. Восстановлено за одно звено Т -дроби при следующих значениях: A min = - 1 . 00000000000000 , F = - 3 . 662217859512357 х 10 ^{- 3} и G = 4 . 159165521519215 х 10 ^{- 2} . Норма L i = 1 . 1 х 10 ^{- 2} . График прообраза смотри на рис. 6. В правом верхнем углу представлен график сравнения точной функции с приближением на интервале t Е [0 , 3] . Визуально его трудно различить от точного, поэтому не указан подробно. Отличие хорошо видно на интервале t Е [3 , 6] , как представлено на рис. 6.

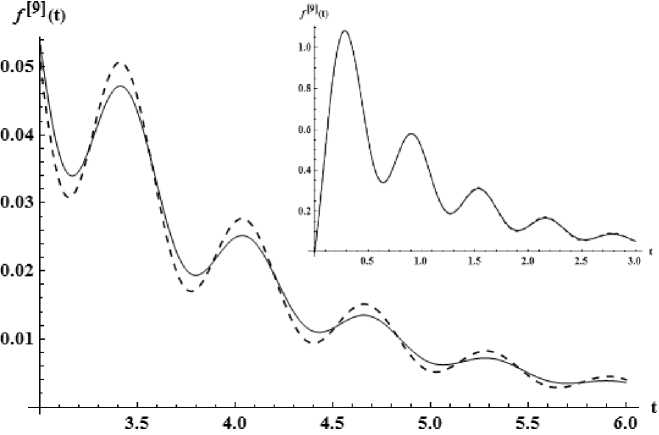
Рис. 7. Приближение девятого порядка – пунктир, точная функция – сплошная линия

Приближение девятого порядка . Образ Лапласа рационального приближения имеет вид [9 / 10] , построенный по набору коэффициентов {с -9 , ..., С 8 } и одного звена Т -дроби. Потребовалось проводить восстановление. Восстановлено за одно звено Т -дроби при следующих значениях: A min = - 0 . 9809843410760894 , F = 3 . 97963410332423 и G = - 2 . 81124280664555 . Норма L i = 1 . 0 х 10 ^{- 2} . График прообраза смотри на рис. 7. В правом верхнем углу представлен график сравнения точной функции с приближением на интервале t Е [0 , 3] . Визуально его трудно различить от точного, поэтому не указан подробно. Отличие хорошо видно на интервале t Е [3 , 6] , как представлено на рис. 7.

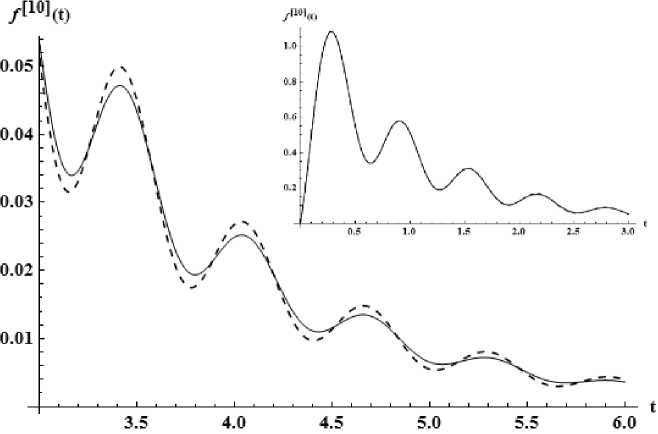
Рис. 8. Приближение десятого порядка – пунктир, точная функция – сплошная линия

Приближение десятого порядка . Образ Лапласа имеет вид [10 / 11] , построенный по набору коэффициентов {с -іо , ..., С 9 } и одному звену Т -дроби. Потребовалось восстанавливать. Восстановлено за одно звено Т -дроби при следующих значениях: A min = - 1 . 00000000000000 , F = 5 . 11710643746204 и G = - 0 . 107835940653098 . Норма L i = 7 . 4 х 10 ^{- 3} . График прообраза смотри на рис. 8. В правом верхнем углу представлен график сравнения точной функции с приближением на интервале t Е [0 , 3] . Визуально его трудно различить от точного, поэтому не указан подробно. Отличие хорошо видно на интервале t Е [3 , 6] , как представлено на рис. 8.

Отметим, что для рассмотренного примера не существует приближение степени [0 / 1] по двум коэффициентам {с —i , С о }, так как с —i = 0 . Кроме того, за одно звено Т -дроби не удается восстановить приближение вида [6 / 7] , которое использует первые 6 моментов и производных. Причины невозможности однозвенного приближения нуждаются в дальнейшем исследовании.

• 6.    Заключение

В работе представлен метод решения систем уравнений марковского восстановления. Процедура получения аппроксимации, как правило, даёт положительный результат, однако не гарантирует его.

Тем не менее описанный в работе метод решения обладает рядом достоинств. Для ряда приложений асимптотические ряды являются конечной целью, и восстановления аналитической аппроксимации не требуется.

Результаты, описанные в данной работе, лежат в основе численного решения уравнений марковского восстановления в программе CRA. Авторы ПК CRA: Коваленко О.В., Седов Д.Б. и Хочкин Н.И.

Продолжается работа над совершенствованием алгоритмов восстановления аппроксимирующих решений с заданными значениями моментов и производных в нуле для его большей надежности с точки зрения гарантирования положительного результата восстановления.