Решение уравнений математической модели рулевого управления с усилителем гидравлического типа

Рост скорости движения автомобилей и стремление к унификации рулевых управлений автомобилей приводят к созданию новых устройств усилителей рулевого управления. Эксплуатация автомобилей происходит в различных дорожных условиях. Поэтому в каждых конкретных условиях необходимо обеспечить приспособление к ним рулевого управления путем создания усилия на рулевом колесе следящего действия. Конструктивно это можно наиболее просто достичь изменением давления в системе гидравлического усилителя.

Для разработки математической модели рулевого управления, использована схема рулевого управления автомобиля Урал-4320 (рис. 1), которая отражает конструкцию и работу рулевого управления и его основные элементы, характерные для большого класса грузовых автомобилей высокой проходимости. Использованная модель рулевого управления с гидравлическим усилителем, обеспечивающим переменное реактивное действие, позволяет определить основные характеристики работы рулевого управления с гидравлическим усилителем. И по ним анализировать приспособленность рулевого управления к различным условиям движения и к конструктивным изменениям рулевого управления при модернизации автомобиля. Оценка адекватности модели сравнением расчетных и экспериментальных результатов приведена в [2].

Использованная математическая модель рулевого управления с гидравлическим усилителем представлена уравнениями, отражающими характеристики и работу основных конструктивных элементов [2]: уравнение движения поршня гидроцилиндра, уравнение движения управляемых колес, уравнение баланса расходов жидкости для распределителя, уравнение перемещения распределителя. Решение такой достаточно сложной математической модели возможно с использованием ЭВМ. Инструментом решения математической модели выбрана программа MathCAD [1].

Изменение усилия на рулевом колесе, обеспечиваемое гидроусилителем рулевого управления, представлено в методике расчета тремя этапами работы.

Этап 1. Усилие на рулевом колесе до включения усилителя в работу. Этап выполняется при условии

[ P CB + F p • Р 1 + P fr + c l • x r ]• r r • k a ^ M c ,                                                      ⁽¹⁾

L                             J           urp •nrp где PCB – усилие сжатия центрирующих элементов, Н;

F p – площадь реактивных плунжеров, м²;

P fr – сила трения в приводе распределителя, Н;

• c 1 – жесткость центрирующих элементов распределителя, Н/м;

• x r – перемещения распределителя, м;

• r r – радиус рулевого колеса, м;

• k _a - коэффициент передачи по углу поворота рулевого колеса;

M c – момент сопротивления поворота колеса, Н/м;

• u rp – передаточное число рулевого привода;

П _Гр — кпД рулевого привода;

р ь р 2 — давление рабочей жидкости в правой и левой полостях силового ц илиндра соответственно, Па.

Усилие на рулевом колесе для этого этапа:

d y •«• J r + ([ ^р св + F p • P s + P fr + c i • x r ^] • r r • k _а +   M^— ) • Sign ⁽ P .)

• , ₌ dt^{1                    p J}                    up -n rp

  
  

r r r где а - угол поворота рулевого колеса, рад; ps - давление слива рабочей жидкости, Па.

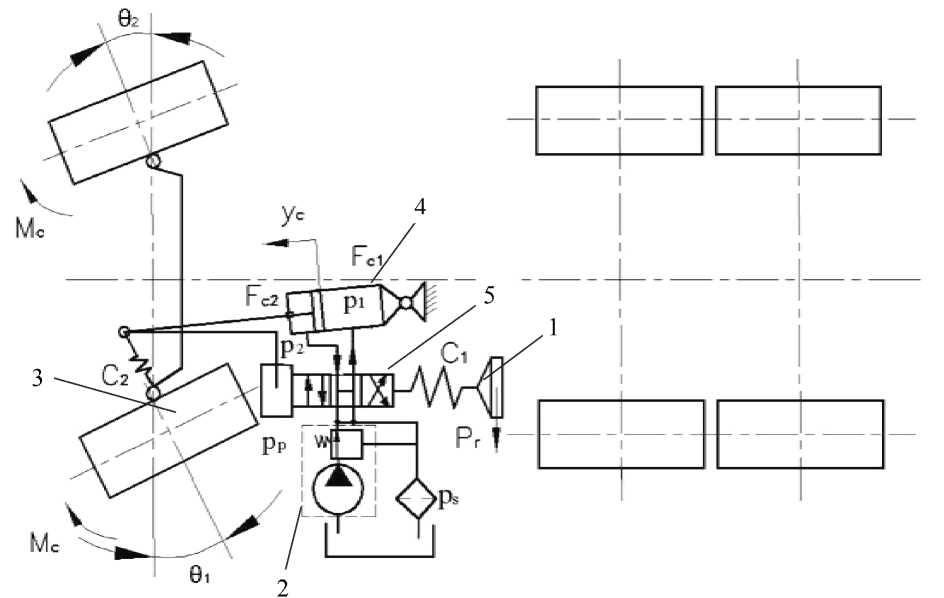
Рис. 1. Схема рулевого управления автомобиля Урал-4320:

1 – рулевое колесо; 2 – гидронасос с регулятором давления; 3 – управляемые колеса;

4 – силовой цилиндр; 5 – гидрораспределитель

Этап 2. Усилие на рулевом колесе за счет действия реактивных элементов. Условие выполнения 2-го этапа:

^{[ P} CB + F p • P i + P fr + c i • x r ]• r r • k a <  M c <

L                              J urp ’nrp                                                          (3

• < ^[ F c 1-- ^{p i}-- P CB - F p • p i ^- P fr - c i • x r ^] • r r • k a ,

urp •П rp где Fci, Fc2 - правая и левая площади поршня соответственно, м2.

Усилие на рулевом колесе для этого этапа:

d y •«• J r + ^[ P CB + F p • p s + P fr + c i • x r ^] • r r • k a • sign ^{( P}r )

P_r = dt -------------------------------------------------------.'                                 (4)

rr

Этап 3.Усилие на рулевом колесе за счет суммирования физического усилия водителя и усилия, развиваемого реактивными элементами. Условие выполнения:

Расчет и конструирование

[ F_c 1 ⋅     ^p 1     - P_CB - F_p ⋅ p 1 - P_fr - c 1 ⋅ x_r ] ⋅ r_r ⋅ k _α ≤ ^c .

• u rp ^⋅η rp                                                u rp ^⋅η rp

Для третьего этапа усилие на рулевом колесе:

• ^d  ⋅α⋅ J_r + ( F_c 1 ⋅    ^pp   - [ P_CB + F_p ⋅ p_s + P_fr + c 1 ⋅ x_r ] ⋅ r_r ⋅ k _α -    ^Mc  ) sign ( P_r )

• dt 2                  u rp ^⋅η rp                                                 u rp ^⋅η rp

Pr =

r

Математическая модель представлена в обобщенном виде для различных типов, конструкций и размеров рулевых управлений с усилителем гидравлического типа. Для приспособления модели для конкретного автомобиля и конструкции рулевого управления необходимо для решения ввести в исходные данные их характеристики в виде постоянных величин: P CB = 100 Н; P fr = 30,74 Н; F p = 0,0003 м²; M c = 210 Нм; u rp = 21,5; η rp = 0,68; P s = 3 МПа; J r = 9,9·10^-2 кг/м²; с 1 = 16680 Н/м; k _α = 1,1; r r = 0,255м; µ r 1 = 0,057; µ r 2 = 0,057; d r = 0,050 м; ρ = 9000 Н/м³; V 01 = 0,0008 м³; V 02 = 0,0008 м³; F c 1 = 0,00385 м²; F c 2 = 0,00177 м²; k = 18,6; V 1 e = 0,00065 м³; V 2 e = 0,00065 м³; B q = 12 МПа; m c =1,35 кг; c 2 = 8,6·10⁵ Нм/рад; r p = 0,19 м; P tc = 18 Н; J k = 61 кг/м²; l 0 = 0,440 м; M t = 179,928 Нм; P r = 50 Н.

Для расчета необходимо принять и задать в исходных данных регулируемый параметр, изменение которого обеспечит заданную траекторию движения автомобиля в определенных условиях. На автомобиле Урал-4320 имеется регулятор давления рабочей жидкости. Поэтому за такой параметр принимаем давление рабочей жидкости.

Для описания процесса функционирования рулевого управления введем условия, ограничивающие максимальное значение переменных.

Регулируемое давление, создаваемое насосом гидроусилителя, ограничим максимальной величиной p_p ≤ p max , достижимой по характеристике насоса, давление слива рабочей жидкости примем больше или равным давлению насыщенных паров p_s ≤ p min . Основным способом обеспечения переменного реактивного действия примем регулирование максимального давления, создаваемого насосом.

Переменные величины в исходных данных: p_p – максимальное давление рабочей жидкости, Па; p_s – давление слива рабочей жидкости, Па.

Проведем проверочные расчеты для следующих сочетаний переменных, охватывающих область возможных режимов работы рулевого управления автомобиля УРАЛ-4320:

P s = 0 МПа, P p = 0 МПа, P p = 10 МПа, P s = 0,3 МПа,

P p = 2 МПа, P s = 0,3 МПа,

P p = 3 МПа, P s = 0,3 МПа,

P p = 4 МПа, P s = 0,3 МПа,

P p = 5 МПа, P s = 0,3 МПа,

P p = 6 МПа, P s = 0,3 МПа,

P p = 7 МПа, P s = 0,3 МПа,

P p = 8 МПа, P s = 0,3 МПа.

Начальные условия: примем в исходный момент времени, t = 0 перед началом поворота автомобиля и в конце его прямолинейного движения:

α( t ) = 0; α`( t ) = 0; y c ( t ) = 0; y c `( t ) = 0; θ с ( t ) = 0; θ с `( t ) = 0; p 1 ( t ) = 0,14·10⁶; p 2 ( t ) = 0,3·10⁶.

Для численного интегрирования необходимо задать набор точек, в которых нужно найти решение уравнений математической модели, в системе MathCAD записываем систему уравнений и неравенств в специальном виде (7).

Используем численный метод интегрирования Рунге-Кутты четвертого порядка.

На рис. 2, 3 представлены некоторые результаты расчетов для условий: усилие на рулевом колесе P r = 50 Н; давление в системе P p = 2 МПа, которое по экспериментальным результатам обеспечивает наибольшую скорость входа автомобиля УРАЛ-4320 в поворот на обледенелой дороге [2].

Численное интегрирование уравнений производилось в течение времени, которое необходи- мо затратить на поворот управляемых колес из нейтрального положения в крайнее левое. Не обнаружено на исследованных режимах колебаний в системе, которые могут возникать при определенных условиях [4]. Перемещение поршня после 3 с (см. рис. 2) характеризуется упругостью рычага. Различие расчетных и экспериментальных данных [2] не превышает 5 %.

Pr =

d 2

— a • Jr + Г рсв + Fp • ps + Pfpr dt2         U-

1 ^xr

^Mc u rp • ^П rp j

[ PCB + Fp • Pl + Pfr + ci • xr ]• rr • ka ^

dp a Jr + [ PCB + Fp • ps + Pfr Pr = -^--------------------------

rr

Mc urp • Пrp ’ ci • xr ]• rr • ka • sign (Pr )

;

• sign ( Pr )

;

r

M

I P CB + F p • p i + P fr + c i • x r I • r r • k a <---------<

^{L                               J}           urp •n rp

Fci--p1      PCB - Fp ' p1 - Pfr - ci • xr urp • n rp

• r • к ' 'r a; ,

d ²

—— a • Jr + dt2 r

P r =----------

F c i •

p p

-

u rp • ⁿ rp

fr ⁺ c i • x r

M c

a

u rp • ⁿ rp j

sign ( P r )

r

r

Fc 1p1PCB - Fp ' pi - Pfr - ci • xr urp • n rp

c rr ,v a — urp • nrp

yc

e с

sign ( P r ) • ( F c i • p i ^- F c 2 • p 2 )

-

cl ( \ . Ус — ( y_e ) + a tan —

c 2

p [ mc

tc

;

Г P r' r r u rpp •n rp + sign ( P r ) • [

c 2 •

Г           (v Y -e e + a tan — F [               U r p ).

- M t - M c ]                  ]

( d Y • sign 1 ЧТ.У с 1 U dt J

J k

^p r i -ⁿ ' d r   ² • ( k a ^^a- k e ^^e c ) • Vl P p - p i I • sign ( P p - p i ) - F c i • dy e

v P                                                         dt

V 0i + F c i • Ус + V i e

B

q

F c 2 • ddty c ^-p r 2 -ⁿ' d r ’^1 •( k a ^^a- k e ^ c ) • Vl p 2 - P s i ’ sign ( p 2 - P s ) V 02 - F c 2- y c + V 2 e

B q

Расчет и конструирование

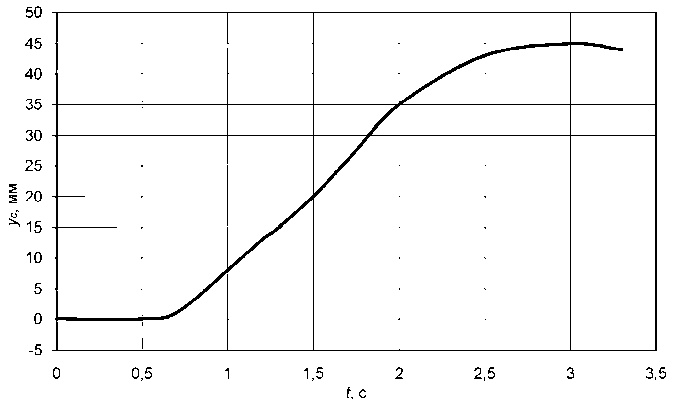
Рис. 2. Перемещение поршня силового цилиндра по времени: y c – перемещение поршня силового цилиндра, t – время за которое перемещается поршень цилиндра

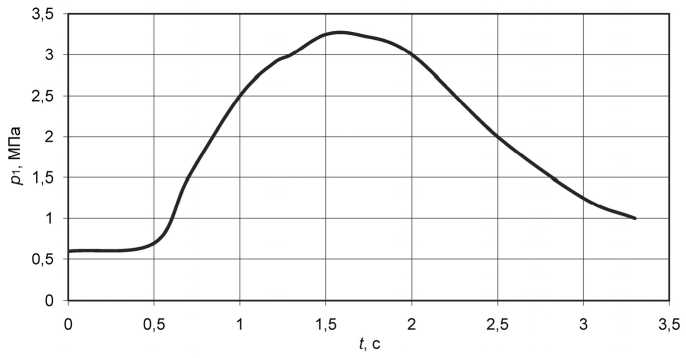
Рис. 3. Изменения давления рабочей жидкости в правой полости силового гидроцилиндра: p 1 – давление рабочей жидкости в правой полости силового гидроцилиндра, t – время, за которое происходит изменение давления

Выводы

• 1.    Решение уравнений математической модели возможно в системе MathCAD и дает подробную информацию по работе рулевого управления. Различие расчетных и экспериментальных данных [2] не превышает 5 %.

• 2.    Не обнаружено на исследованных режимах колебаний в системе, которые могут возникать при определенных условиях [4].

• 3.    Чтобы получить возможность оценки движения автомобиля в целом, необходимо объединить модель автомобиля с моделью рулевого управления.