Решение уравнения геодезической в индуцированной теории модифицированной гравитации для случая космологических моделей

Введение. Уравнения МТИГ

В данной статье рассматривается одна, из актуальных проблем современной космологии: проблема. истинного значения скорости расширения Вселенной. Значение, полученное различными учеными и группами учёных, далеко от их рекомендаций. В 1998 году Адам Рисе и компания получили для постоянной Хаббла значение 65, 2 км/с/Мпс [1]. Ещё одна наблюдение, проведённая А.Рисе в 2016 году оценивает значение постоянной Хаббла порядка 73 км/с/Мпк данные европейского телескопа Планка дают значение 67/км/с/Мпк значение, которое не совпадает с тем, что дает телескоп Хаббла [2]. Фактическое значение постоянной Хаббла колеблется между 63 км/с/Мпс и 73 км/с/Мпс. Такое расхождение в наблюдениях требует своего объяснения.

Наша модель основана, на. теории иидуцироваииой гравитации изложенной в работах [3-5], в которых вводится в начальном действии квадратичное поле Y = (X,X ) = X^AX ^вт]ав, индуцирующие обе гравитационные и космологические постоянные. Функции X ^А = X^А(ст ^ ), где А, В = 1, 2,..., D, ц, v = 0,1,..., п— 1, отображают n-мерное Риманово многообразие, описываемое метрикой д^ , в D-мерное плоское пространство-время с метрикой ^ ав [3]. Можно просто считать что имеется мультиплет скалярных полей X ^А(ст^ц). В дальнейших вычислениях мы положим n = 4. Эффективное космологическое и гравитационное постоянные связаны с Y по следующей формуле:

гас3       „     с3         .           1 , „

' = ± WIYK  G  8^,    Л  = 2^(—В + Ueff), П = 4          W где Й — постоят гая планка, с — скорость света. В = Во — wey. еу — энергия вакуума. Во. га. ф — постоянные теории, Uejj = Uejj(Y) — эффективный потенциал теории.

Обобщение эйнштейновской теории строится исходя из действия [5]:

So = - [ {№,X ) га

+ U + L m (X, s )}V-gdⁿ^,

(П)

где R — скалярная кривизна по метрике g _v^. U = U(X ^А) — потенциал зависящий от поля Y. ф га — некоторые постоянные взаимодействия. L _m (X,S) — характеризует всевозможные взаимодействия X^A с другими полями материи.

В предыдущих работах [4], [5] рассматривался квадратичный потенциал по полю Y: U = U(Y) = Y2 А + Yfw — В. Варьированием по д„и. из (II), для системы с материей, были получены следующие самосогласованные уравнения:

G _ap = 2^^Ug “P ⁺ у [^“^4 ^{— g} «P 4^Y

Ш-т,. 2 ^y Y^e)“⁴,

(Ш)

где G _ap — тензор Эйнштейна; T( _e ) _ap — тензор энергии-импульса (ТЭИ) полей материи (например, идеальной жидкости).

Следствием этих уравнений является закон сохранения энергии, имеющего вид:

V p Y • (^R + Ц) — raV“T₍“_e)4 = 0.

(IV)

Уравнения (III) — есть аналог уравнений Эйнштейна для макроскопической среды.

Как следует из (IV), при Y = const уравнения сводятся к уравнениям Эйнштейна (ES -стадия). Мы заметили, что для случая Y = const (стадия RS) появляется уравнение, которое исчезает для стадии ES. Таким образом, мы также исследуем решения, содержащие переходы от ES к RS и наоборот. Как показано в предыдущих работах, такие решения напоминают фазовые переходы и содержат элементы стохастичпости [4].

1. Уравнения для метрики Фридмана-Леметра-Робертсона-Уокера

Рассмотрим уравнения (III) для случая квадратичного потенциала скалярного поля U (Y) = K x Y ² + /_WY — В, В = const, для случая однородной и изотропной космологической модели, с метрикой g_v^_ задавасмой 4-иптсрвалом:

dr2

ds² = dt² — a²(t)[  --- -—2^ + T²(t)dU²^,                          (1-1)

где ко = 0,1, —1 соответственно, для плоской, закрытой и открытой модели Вселенной, dfi2 = d26 + sin29d?^ — метрическая форма единичной сферы. Было показано, что статические решение Y = Yo = const, приводящие к эйнштейновской теории, могут быть неустойчивыми и решения переходят в колебательный режим, в окрестности точки Y = Yo, что приводит к осциллирующему решению для масштабного фактора a(t) и параметра Хаббла Н = а /а. Например, на рис. 1 показаны характерное поведение нормированных функций масштабного фактора, и параметра. Хаббла, для случая Y = const. Как следует из рисунков, не монотонные изменения масштабного фактора и параметра. Хаббла, могут привести к ошибочной интерпретации наблюдательных данных. Поскольку космологическое красное смещение z(t) = .o/.(t) — 1 фотонов зависят от значения масштабного фактора в момент времени t, соответствующего моменту испускания. Исходя из красного смещения вычисляются расстояния до космологических объектов. В работах [3], [4] рассмотрены также более сложные случаи связанные со случайными переходами решений со стадии Y = const в стадию Y = const. Исходя из изложенного является актуальной задачей исследования геодезических линий в пространстве-времени Фридмана, для предлагаемой модели.

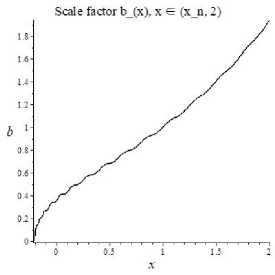
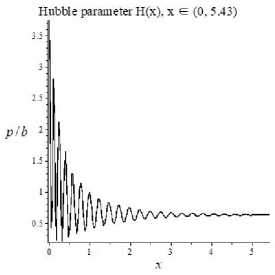
Рис. 1. (а) эволюция масштабного фактора во времени; (б) эволюция параметра Хаббла во времени.

Уравнения (III) после некоторых преобразований можно привести к следующей системе дифференциальных уравнений, на нормированный (на современное значение йо) масштабный фактор b(t) = .(t)/._o и скаляр ное поле Z (t) = Y (t)/Y₀, нормированное на средне вакуумное значение [4]. Также вводится собственное время х = t/to нормированное на возраст Вселенной to.

a ( ^p . Р2 . k b ⁺ b^{2 +} b²

Zo

(Z ^— 0 (^{B1 +} 8 ⁺ A) ^{+ K} ■ = ^0,

Р = b,

(1.2)

Z p  p2   k

Zb ⁺ b^{2 +} b²

I ( I —1)2 ( b -

Z \Z0

P p    p r\

+ b3 + b4

+ Key = 0,

(1.3)

которые решаются численно, для различных значений постоянных параметров ( B1,p _r ,K _rv ..) теории. В данной феноменологической модели вводится взаимодействие скалярного поля Z (t) с идеальной жидкостью [4,5] и В1 = В/(6 £).

Упрощаем тензорные уравнения геодезических линий, на плоскости эклиптики 9 = тт/2 :

d2xг       dxk dxl

(1.4)

ds2      kl ds ds ’ где Г^ — символы Кристоффеля по метрике дир-\ хг = (t,r, 9,ф). Два уравнения из системы (1.4)

можно один раз проинтегрировать и получим:

ds^ф   г² й² ’

d dA =

^{е +} й² ’

(1.5)

где s — параметр вдоль геодезической, L_v, C t — постоянные интегрирования, имеющие смысл углового момента и параметра связанного с полной энергией, е = 1, 0 — для времеипоподобиой или изотропной линии. Приведем оставшиеся уравнения:

(dxr (Х)) '     (Х)2+ 1)       (b(X))2) (1    (г(х))2)’                     (1'6)

dX2 ^{Г (Х)} = е„ (b (х:))² + 1 (" (2 ^е" ^{(b (Х))}2 ⁺ 1)(dX^{r (Х)}) ^{Hb (Х) +} —r3 (b0(+))² ) ’       ^(L7)

где НДж) = ^d^) g^ = ^da^) ^у = Н (t) • to - нормированный (на возраст Вселенной) параметр Хаббла, т² = L^/C t ,е_п = e)C_t.

В общем случае, численными методами решаются системы уравнений (1.2), (1.3) и (1.5)-(1.7). Однако, аналитически проанализированы частные случаи C _t = 0 и L _v = 0. Уравнение для нахождения вида, траектории имеет вид:

( d ⁽^

(г (ф))² (1 - ко (г (ф))²^ ((г (ф))² — т²) т²

(1.8)

Исходя из уравнения (1.8), делаем вывод, что траектория геодезической не зависит от масштабного фактора. От масштабного фактора, зависят лишь динамические параметры, такие как скорости пробных тел, зависимости г = г(t), ф(t). Последнее уравнение можно решить. Например, интересный вывод мы получили проанализировав решение этого уравнения для закрытой модели ко = 1.

Решение имеет вид:

г(ф) = ±                          ----;

(1.9)

т² + 1 + |т² — 1| 8гп(2ф)

В полярное системе координат это есть уравнение эллипса. При т2 = 1 эллипс является окружностью радиуса 1. Интересно, что это решение распространяется и на область 1 < г2 < т2, если т2 > 1. Для значений параметров т2 < 1 следует г2 < 1 (рис. 1). Геодезические нарушают пер воначальную сигнатуру пространства-времени, поскольку компонента метрики дг1 меняет знак при переходе через гиперповерхность г2 = 1. В стандартной закрытой космологической модели считается, что г2 < 1 и используется переход к координате %, г = sinx-

Заключение

Таким образом, мы получили что масштабный фактор, параметр Хаббла, а. также зависимость красного смещения от времени могут носить колебательный характер, например, как показано па. рисунке 1. Это может приводит к не совсем правильной интерпретации наблюдательных данных, в том числе и к неточности измерению расстояния исходя из красного смещения. При этом сами траектории геодезических линий не зависят от масштабного фактора. Для закрытой модели распространение метрики на область 1 < г²<  т² требует теоретического обоснования и возможно новых топологический не тривиальных однородных и изотропных моделей, в которых существует граница г² = 1, а к этой границе «приклеено» другое многообразие. Стандартно принято представлять трёхмерную часть закрытой модели как сферу в четырёхмерном евклидовом пространстве. Возникает вопрос об расширении такого представления с геометрической точки зрения, пока, не затрагивая физическую сторону.