Решение внутренней задачи для конечной регулярной двумерной решетки спиральных элементов, возбуждаемой плоской электромагнитной волной
Автор: Табаков Д.П., Аль-нозайли Б.М.А.
Журнал: Физика волновых процессов и радиотехнические системы @journal-pwp
Статья в выпуске: 3 т.27, 2024 года.
Бесплатный доступ
Обоснование. Работа направлена на развитие и исследование строгих методов решения внутренней задачи электродинамики для многоэлементных структур (метаструктур), состоящих из конечного числа элементов, а также на исследование протекающих в них физических процессов. Частным случаем подобных структур являются двумерные решетки с фиксированным межэлементным расстоянием, состоящие из одинаковых элементов, имеющих одну и ту же пространственную ориентацию (регулярные решетки).
Метаструктура, спиральная структура, интегральное уравнение фредгольма, тонкопроволочное приближение, интегральное представление электромагнитного поля, резонанс, распределение тока, метод гаусса - зейделя, метод собственных функций
Короткий адрес: https://sciup.org/140307120
IDR: 140307120 | УДК: 537.862 | DOI: 10.18469/1810-3189.2024.27.3.17-33
Текст научной статьи Решение внутренней задачи для конечной регулярной двумерной решетки спиральных элементов, возбуждаемой плоской электромагнитной волной
Одной из наиболее актуальных задач электродинамики является исследование процессов, протекающих в многоэлементных излучающих и переизлучающих структурах с последующим определением характеристик создаваемых и рассеиваемых ими электромагнитных полей (ЭМП) соответственно. В первом случае принято говорить о задаче излучения, во втором – о задаче дифракции ЭМВ. Исследование процессов, протекающих в структурах, предполагает определение токовых функций, носителями которых выступают элементы структур, что составляет суть внутренней задачи электродинамики. Определение характеристик ЭМП, порождаемых токовыми функциями, составляет суть внешней задачи электродинамики.
Актуальность задачи, обозначенной в самом начале, связана с ее очень большой общностью. Так, под многоэлементными излучающими структурами можно понимать любые структуры, имеющие более одного элемента – носителя токовых функций. Это определение включает подавляющее
[@^Н © Табаков Д.П., Аль-Нозайли Б.М.А., 2024
большинство используемых на практике антенн, и наиболее ярким примером здесь являются фазированные антенные решетки. Под определение многоэлементных переизлучающих структур попадают киральные структуры [1], фотонные кристаллы [2], дифракционные решетки, некоторые типы замедляющих структур и линз диапазона СВЧ, а также любые материальные среды, рассматриваемые на микроскопическом уровне. Все перечисленные переизлучающие структуры, за исключением последних, можно отнести к метаструктурам (метаматериалам). Метаматериалы синтезируются внедрением в исходный природный материал частиц с самыми различными формами, которые модифицируют диэлектрическую и магнитную восприимчивость исходного материала. Свойства метаматериалов обусловлены периодической микроструктурой, создаваемой человеком. Основополагающей работой по метаматериалам можно считать работу [3] В.Г. Веселаго. Метаматериалы могут обладать свойствами, принципиально отсутствующими у естественных материалов, встречающихся в природе, например отрицательным коэффициентом преломления [4] (левосторонние материалы). Подобные материалы были изобретены и продемонстрированы Д.Р. Смитом и сотрудниками калифорнийского университета в Сан-Диего [5] спустя более чем 30 лет после публикации статьи В.Г. Веселаго. В основу были положены работы Дж.В. Пендри [6–8]. В настоящее время метаматериалы находят применение в СВЧ- и антенно-фидерных устройствах, позволяя улучшить их параметры. В обзоре [9] представлены результаты, касающиеся применения метаматериалов при построении СВЧ-устройств и антенн. Примером метаматериалов другого рода являются фотонные кристаллы [2], на основе которых можно создавать оптические фильтры, волноводы и многие другие устройства.
Одним из наиболее важных вопросов, возникающих при анализе многоэлементных излучающих и переизлучающих структур, является учет межэлементных взаимодействий. Без решения этого вопроса невозможно построение адекватных математических моделей структур. Под адекватностью будем понимать корректность качественного и количественного отображения математической моделью процессов, происходящих в структуре. Эффективная математическая модель может существенно сократить время и ресурсы, затрачиваемые на анализ либо синтез структуры с требуемыми характеристиками.
На протяжении развития электродинамики, оптики и техники СВЧ-устройств появилось достаточно большое количество соответствующих методов, имеющих свои достоинства и недостатки. Долгое время в инженерной практике для расчета взаимодействия в многоэлементных излучающих структурах использовался метод наведенных ЭДС. Основные принципы этого метода изложены в работе [10]. Метод наведенных ЭДС позволяет находить наведенные собственные сопротивления элементов антенны, а также амплитуды и фазы токов в пассивных элементах. Из недостатков метода отметим, что он накладывает определенные ограничения на длину и расстояние между элементами в силу использования приближенных распределений тока. Сейчас для решения подобных задач применяют системы автоматизированного проектирования (САПР), использующие в своей основе метод моментов [11], метод конечных элементов и метод конечных разностей [12]. К недостаткам такого подхода можно отнести высокие требования к ЭВМ и стоимость программного обеспечения, отсутствие математической модели анализируемой структуры в явном виде.
Что касается метаматериалов, то здесь также можно использовать САПР с уже упомянутыми достоинствами и недостатками. Для метаматериалов значительных либо неограниченных волновых размеров с регулярной структурой наиболее эффективным вариантом является применение строгих методов, использующих в своей основе периодические граничные условия. Упрощенный подход к анализу предполагает использование методов теории цепей (эквивалентные схемы), а также эффективных диэлектрических и магнитных проницаемостей. Для метаструктур больших волновых размеров для анализа целесообразно использовать оптические и квазиоптические методы. При этом в обязательном порядке необходимо обоснование адекватности упрощенной модели исследуемой структуры [13].
Таким образом, разработка универсальных методов расчета межэлементного взаимодействия является актуальной задачей. В [14] рассмотрен итерационный подход к решению интегральных уравнений теории проволочных антенн на основе многошагового метода минимальных невязок. Здесь метод применялся непосредственно к общей матрице системы линейных алгебраических уравнений (СЛАУ). В [15] в качестве основы для расчета взаимодействия было предложено использование модификации метода Гаусса – Зей- деля [16] для случая блочной матрицы СЛАУ. Метод применен для решения задачи дифракции на метаструктуре – тонком слое конечных размеров, состоящем из двойных разомкнутых колец. Сделан вывод, что предложенный метод может быть эффективен для расчета метаструктур, имеющих конечные размеры. В [17] рассмотрена задача дифракции плоской электромагнитной волны на киральном слое, представляющем собой прямоугольную эквидистантную решетку 10 х 10 элементов, сотоящую из пятисегментных S-элементов. Показано, что, несмотря на довольно малое количество хаотически ориентированных S-элементов, диаграммы рассеяния имеют вполне детерминированный характер. В [18] материалы статьи [15] были дополнены алгоритмами расчета элементов блочной матрицы СЛАУ для случая построения структуры из однотипных элементов, обладающих различными видами симметрий. Показано, что данные алгоритмы позволяют существенно сокращать время расчета. В [19] рассмотрен вопрос использования метода [15] для расчета распределений токов на директорной антенне [20]. Доказано, что для директорной антенны в исследуемом диапазоне частот метод обладает хорошей сходимостью. В [21] исследована возможность использования итерационного подхода к решению внутренней задачи для симметричного вибратора с рефлектором из параллельных прямолинейных проводников. Вместе с этим представлен ключевой алгоритм расчета элементов блочной матрицы, имеющий линейную оценку сложности в зависимости от числа элементов рефлектора, даны рекомендации по выбору систем проекционных функций и учету имеющихся у структуры симметрий. Проведено исследование распределений токов, входного сопротивления и характеристик излучения рассматриваемой структуры.
В настоящей статье рассмотрено решение внутренней задачи для конечной регулярной двумерной решетки, состоящей из конических спиральных элементов. Возбуждение решетки осуществлялось плоской линейно-поляризованной электромагнитной волной. Решение внутренней задачи выполнялось на основе метода, описанного в [15]. Предложен алгоритм вычисления компактной блочной матрицы на основе алгоритмов, описанных в [18]. С учетом влияния резонансных свойств элементов, образующих решетку, на сходимость итерационного процесса, а также с целью обоснования выбора системы проекционных функций в рамках метода моментов проведен спектральный анализ интегрального оператора внутренней задачи для одиночного спирального элемента, суть которого описана в [22]. Приведены результаты спектрального анализа токовых функций для одиночного спирального элемента и для элементов, находящихся в решетке. Исследована сходимость решения внутренней задачи для решетки элементов. Полученным результатам дана соответствующая интерпретация. Определены направления дальнейшего развития темы.
1. Основные расчетные выражения
Основные расчетные выражения были достаточно подробно приведены в [21]. Здесь мы изложим соответствующий материал с уточнением некоторых моментов. Рассмотрим излучающую либо переизлучающую структуру, образованную совокупностью элементов vn, (n е ^: 1...N, N -число элементов), полученных на основе совокупности уникальных элементов vu путем параллельного переноса и (или) вращения (u е U: 1.U, U – число уникальных элементов). Внутренняя задача электродинамики для рассматриваемой структуры сводится к операторной системе вида [19]:
Е Т n , n ( n n ' ) = Z n , n е Я . (1)
n ′
В данной системе Тnn,, n ^ n' - операторы взаимодействия элементов v и v ; Т = Т - соб-n n n,n n ственный оператор элемента vn ; Zn - функции, порождаемые сторонними полями, ηn′ – токовые функции, подлежащие определению. К системе (1) применяется схема метода моментов [11]: с помощью систем базисных {в}n- = {вq'}n' и тестовых {т}n = {тq}n функций (q = qn gQ: 1. Q, q' = = qn , g Q': 1. Q') определяется оператор скалярного произведения функций. Искомые функции
η n ′ аппроксимируются рядами:
η n ′ = ∑ I q ( n ′′ ) β n ′ , q ′ q ′
Относительно неизвестных коэффициентов
( n ′ ) I q ′
формируется система линейных алгебраиче- ских уравнений (СЛАУ) вида
ZI = E .
Здесь Z - блочная матрица обобщенных импедан-сов; I , E - соответственно, блочные векторы неизвестных и правой части,
Z ⊃ z ⊃ Z ( n , n ′ ) =< τΨ ( β )> n , n ′ q , q ′ n , q , n , n ′ n ′ , q ′ ,
I ⊃ i n ′ ⊃ Iq ( n ′′ ), E ⊃ e n ⊃ E q ( n )=< τ n , q , ζ n >.
Элементы блочной матрицы с одинаковыми индексами znn = zn будем называть матрицами собственных импедансов, элементы с разными индексами – матрицами взаимных импедансов. Последние определяют взаимодействие между элементами метаструктуры. Скобки «<> » используются для обозначения скалярного произведения. Введем в рассмотрение массив уникальных матриц {zk} = {z} (k e К.: 1.U...K). Будем считать, что первые U матриц массива {z} являются собственными матрицами импедансов уникальных элементов vu, а оставшиеся K - U элементов – матрицами взаимных импедансов. Массив {p(z),} с элементами p(z), = k будет устанавливать n,n n,n соответствие между парой индексов n, n‘e ^ и индексом k e К. Таким образом, имеем: zn,n′=zk, k=p(nz,n)′∈{p(nz,n)′}≡{p(z)}.
В общем случае, когда структура состоит из хаотично расположенных, отличных друг от друга элемент о в vn , введение представленных массивов { z } и { p ( z ) } не имеет смысла и лишь несущественно увеличивает затраты машинной памяти и машинного времени. Но в случае, когда в структуре имеются однотипные элементы, а также присутствует регулярность в их взаимном расположе- 2
нии, имеет место неравенство K < N , и введение указанных массивов становится оправданным, при этом они, по сути, несут в себе базовую часть априорной информации о структуре. Алгоритм расчета массива уникальных матриц будет рассмотрен далее.
Заключительным этапом решения внутренней задачи является решение блочной СЛАУ (3). В данном случае наиболее рациональным представляется использование итерационных методов, основанных на расщеплении матрицы [16], однако в случае отсутствия диагонального преобладания в матрице Z они не обеспечивают сходимости итерационного процесса.
Достичь сходимости классических итерационных методов можно, рассматривая именно блочную СЛАУ (3) в предположении, что между элементами структуры отсутствует достаточно сильная связь. Также на сходимость итерационного процесса существенным образом влияет выбор систем проекционных функций (СПФ). Оптимальным вариантом в данном случае представляется использование систем собственных функций (СФ) входящих в структуру элементов или СПФ, близких к СФ [23]. Вычисление СФ представляет собой вспомогательную задачу, сложность реше- ния которой определяется числом уникальных элементов vu и их свойствами. Полная проблема собственных значений для матриц собственных импедансов уникальных элементов zu, полученных в рамках метода моментов с помощью базисных функций вuq и тестовых функций Тuq, формулируется в виде zu J(u)= Р(х(u))J(u).
Здесь J ( u ) – матрица, столбцы которой содержат собственные векторы (СВ) матрицы z u ; P ( x ( u ) ) -диагональная матрица, формируемая вектором x ( u ) , элементы ^ q которого являются соответствующими собственными значениями (СЗ) матрицы z u ; Р - оператор, формирующий диагональную матрицу. Операндом Р является вектор элементов главной диагонали либо матрица, элементы главной диагонали которой используются оператором Р для создания диагональной матрицы. Далее будем считать, что для рассматриваемых одиночных элементов комплексные матрицы z u симметричны. СЗ ξ q аппроксимируют СЗ собственных интегральных операторов У u , СФ указанных интегральных операторов аппроксимируются с помощью СВ следующим образом:
Q′ й r( u) (u) (u)
β u , q ≈ ∑ J q ′ , q β u , q ′ , J n , q ∈ J .
q ′ =1
Далее эта задача будет рассмотрена для конического спирального элемента, образующего исследуемую структуру.
Применяя процедуру Гаусса – Зейделя [16] к блочной СЛАУ, можно записать следующую форму ее решения:
( l + 1) ( l ) ( l + 1)
n pn n n,n′n′n,n′n′, l>i l
- 1 p n n , n , n , n ′ p n n , n ′
- соответственно, обращенные собственные матрицы и весовые матрицы; p n выступают в качестве матриц предобуславливателя. В процедуре (4) можно также использовать более простой вариант - 1 p n n , n .
Если положить во второй сумме (4) l + 1 = l , то формула будет соответствовать методу простой итерации. Критерий оценки сходимости строится в соответствии с неравенством:
5 1 = max(| i n + 1) - i nn ) | /1 i ( n + 1) |) <5 * , (5)
n где 5* - сколь угодно малое наперед заданное число. Под | v | здесь и далее будем понимать евклидову норму для вектора v.
-
2. Интегральные представления электромагнитного
поля тонкопроволочной многоэлементной структуры
Многоэлементная тонкопроволочная структура L представляет собой совокупность N тонких проводников Li, L2, ..., Ln произвольной формы, расположенных в свободном пространстве с волновым сопротивлением Wm . Для простоты предположим, что радиус всех проводников одинаков и равен s. Каждый проводник можно описать векторным уравнением, зависящим от натурального параметра l: ˆˆˆ n nyn n, n,min , n,max , где Xn (l), Yn (l), Zn (l) - гладкие функции. Под Ln = = Ln max — Ln min также будем понимать длину n-го проводника. Интегральное представление электромагнитного поля (ИП ЭМП) такой структуры можно записать как [24]:
N
F ( r ) = ЕJ In '( l 'Ж* F )( r , rn'll ')) dl ', F - E , H ; (6)
nLn'
здесь In, ( l ') - распределение полного тока по образующей Ln, ;
-
K ( E ) = W m Г k 2 l ‘ Gdl -£ — r ‘) B\ , ik L 5 Г 7_
K ( H ) = l ' x ( r - r ') B
-
- ядра ИП ЭМП; r ' = r n ‘ ( l ') - векторное уравнение образующей Ln, ; l ' = l n ‘ ( l ')= d r n ‘ ( l ')/ dl' - единичный вектор касательной, определенный в точке l' на образующей ln, ;
exp ( - ikR ) 1 d g ikR + 1
G =---------, B = =--z— G ,
4 n R R d R R 2
R = ^| r - r '|2 +s 2
– соответственно, функция Грина для свободного пространства и ее производная; R – расстояние, регуляризированное радиусом проводников s .
Для In, ( l ') целесообразно представление в виде рядов типа (2). Исходное ИП ЭМП (6) при этом приобретет вид:
F ( r ) = ЕЕ 4 ’) [ в n ', q '( l ') K ( F ) ( r , r n '( l'» dl ', F - E , H ; n' q' n'
На каждой образующей справедливо граничное условие для идеального проводника:
( E (( in ))( rn ( l )) + E ( rn ( l ))) ■ Ц ( l ) = 0. (7)
n nn
Умножая поочередно (7) на тестовые функции т nq ( l ) и интегрируя по l , получаем СЛАУ для вычисления I n ) , по форме совпадающую с (3), в которой:
z q7 ')= J Ь n , q ( l ) ₽ n ', q '( l ^( n , n ')( l , l ') dl'dl ,
LL n n
E ( n ) = l\,( l ) v ( n ) ( l )dl ; q n , q
L
n
ц ( n , n ' ) ( l , l ') = l n ( l ) ■ K ( E ) ( r n ( l ), r n' ( l ')),
v ( n ) ( l ) = l n ( l ) ■ E (( in ))( r n ( l )).
Конкретизируем способ вычисления интегралов в (8) с помощью процедуры сегментации проводников, предполагающей представление n -го проводника в виде совокупности M + 1 узлов L M ) : r n i , r n 2 , . , r nM + 1 . Между узлами с номерами m и m + 1 находится m -й сегмент r n m ( l ), уравнение которого может быть записано в следующем виде:
гп m( l ) = rn т+ ln ml , l € [-\ m/2, Лп m/2]- n , m n , m n , m n , m n , m
Здесь r nm =( r n,m + r nm + 1 )/2 - центр сегмента; , ,,
Л n , m = | r n , m + 1 - r n , m 1 - длина сегмента; 1 n , m =
= ( r n , m + 1 - r n , m )/ Л n , m - единичный вектор касательной на сегменте; здесь и далее индексы m e M : 1...M и m 'e M ': 1... M' будем ассоциировать с сегментами на n -м и n '-м элементе структуры соответственно.
В качестве базисных возьмем взвешенные суммы функций, кусочно-постоянных в пределах каждого сегмента:
О ' ) = Е в n , , ( l n , m W ' ’ . l n , m . Л n , m ), (9)
m где ln,m – значение натурального параметра на сегментированной образующей L(M), соответствующее центру сегмента с индексом m; с( l, l, Л) -функция, описывающая прямоугольный единичный импульс, имеющий центр в точке l и ширину Л. В качестве тестовых будем использовать взвешенные суммы дельта-функций Дирака:
т^ M ) ( l )= тп ( in J5( l - in J. (10)
n , q n , q n , m n , m
m
Такой подход можно рассматривать как обобщенный метод коллокаций [25]. Из представленных выражений видно, что в случае (9) роль весовых коэффициентов играют значения функций В ( l ), вычисленные в точках коллокации l , n , q n , m
а
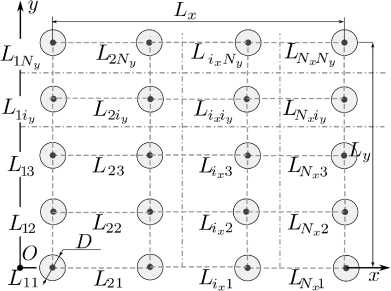
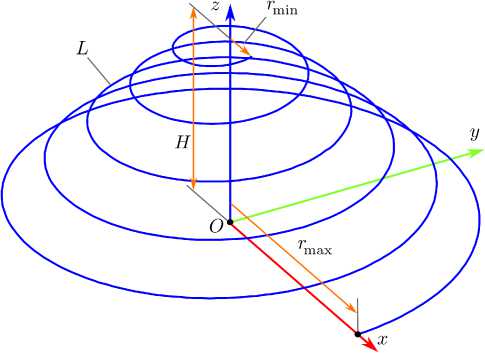
Рис. 1. Геометрия решетки ( а ) и образующих ее элементов ( б )
Fig. 1. Geometry of the lattice ( a ) and its constituent elements ( b )
б
а в случае (10) аналогичная роль принадлежит функциям т n , q ( l ).
Применяя приведенные выражения в (8) с учетом свойств дельта-функции, получаем формулы для расчета матричных коэффициентов и коэффициентов правой части СЛАУ с помощью конечных сумм:
Z q“- УУУ nq (С,» n/ l ,^^ J,I (11)
mm ′
E(n )^Y г (/ )v< n ), q n,q n,m m ,
m здесь:
n J y=t H ( ” ’ " ')( n.m,JdT. v j ? = v ( n )( l„ , „,).
∆ n ′ , m ′
Традиционному методу коллокаций соответствует выбор:
в n,q
3. Исследуемая структура Геометрия исследуемой метаструктуры (общий вид) приведена на рис. 1, а, геометрия образующих ее элементов – на рис. 1, б. Структура представляет собой решетку с прямоугольной сеткой, лежащую в плоскости xOy. Общий размер метаструктуры можно определить как Lx х Ly. В узлы решетки помещены переизлучающие элементы, имеющие одинаковую форму и одинаковую пространственную ориентацию, что с учетом фиксированного межэлементного расстояния позволяет считать решетку регулярной. Размер переизлучающих элементов не превышает значения D. Возбуждение переотраженного излучения осуществляется плоской электромагнитной волной (ПЭМВ), имеющей линейную поляризацию. Угол падения ПЭМВ на структуру может иметь произвольное значение. Стороннее электрическое поле E( 1П), порождаемое волной, возбуждает токи, распределяющиеся по переотражающим элементам. Эти токи становятся источниками ЭМП, создаваемого метаструктурой. Проведем детальное рассмотрение решетки метаструктуры. Для узлов решетки и соответствующих элементов решетки удобно применять двойную индексацию. Индексы вдоль соответствующих осей будем использовать обозначения ix, iy. При заполнении итоговой матрицы СЛАУ осуществляется переход от двойной к сквозной индексации (n = 1. N): n = ix + (iy -1)Nx, ix =1,...,Nx, iy =1,...,Ny. (13) Рассмотрим параметры, задающие геометрию решетки. В дальнейшем hx и hy будут означать расстояние между соседними элементами. С использованием этих обозначений можно вычислить координаты узлов решетки: Г i = x (hx (ix -1) - Lx/2) + y (hy (iy -1) - Ly/2). x,y Обозначения N и N будем использовать для xy числа элементов вдоль соответствующих осей. В этом случае: Lx=(Nx-1)hx, Ly=(Ny-1)hy. Элементы Lii метаструктуры – конические x, y спирали, образованные идеальным проводником, Рис. 2. Связь плоской электромагнитной волны W с первичной волной W′ и глобальной декартовой системой координат Fig. 2. Relationship between a plane electromagnetic wave W and the primary wave W′ and the global Cartesian coordinate system имеющим круглое сечение. Ось каждой спирали параллельна оси Oz. Сам элемент показан на рис. 1, б. Минимальный радиус спирали – rmin , максимальный радиус спирали – rmax . Высота спирали равна H число витков обозначим как Nl . Осью спиральных элементов будем считать линию, совпадающую с осью Oz. Диаметр проводников 2ε существенно меньше λ и существенно меньше размера спиралей и межвиткового расстояния. Это позволяет использовать тонкопроволочное приближение при построении модели метаструктуры (выражения, приведенные в предыдущем разделе). Общее уравнение конической архимедовой спирали имеет вид L:r(t)=(rmax-hrt)cos(st)xˆ + +(r -h t)sin(st)ˆy+h tˆz, max rz t∈[0,2πNl]. Здесь t является ненатуральным параметром; rmin , rmax – соответственно минимальный и максимальный радиус спирали; H - ее высота; Nl – число витков. С помощью hr обозначен радиальный коэффициент намотки, с помощью hz – коэффициент намотки по высоте. Параметр s =±1 позволяет изменять направление намотки спирали, что дает возможность использовать приведенное параметрическое уравнение для анализа соответствующих киральных структур (левых и правых). Переменные hr и hz можно вычислить при заданных rmin, rm , H и Ni с помощью следующих формул: hr= г —г ■ м max min h= 2πNl,z2πNl. Для определения натурального параметра на конической спирали следует использовать выражение l(t)=∫t |l(t′)|dt′, 0 в котором l(t) = dr(t)/ dt - касательный орт, определенный в точке r(t) образующей. Таким образом, уравнение образующей конической архимедовой спирали, имеющего запись в натуральном параметре, можно получить с помощью (14), где следует использовать подстановку t→ t(l). Для функции t(l) на конической архимедовой спирали не существует явного выражения, поэтому она может быть определена только численно с использованием выражения (16) на основе метода обратной интерполяции [16]. Любой элемент Lii решетки x, y может быть получен согласно выражению: (z) Lii:rii(l)=R(φii)r(l)+rii. (17) x,y x,y x,y x,y (z) Здесь R (φ) – матрица поворота вокруг оси Oz на угол ф. Далее можно перейти к сквозной нумерации (13) и использовать для расчетов выражения, приведенные в предыдущем разделе. Поле ПЭМВ W (рис. 2) имеет следующий вид: E(in)(r)=pˆE0exp(-ikr+ψ0), H(in)(r)=[kˆ×pˆ] E0 exp(-ikr + ψ ). Wm Здесь k = k k , к является волновым ортом; к используется для обозначения волнового числа; E0 – амплитуда вектора электрического поля; Wm - волновое (характеристическое) сопротивление среды; ψ0 – начальная фаза волны; pˆ – вектор поляризации, определяющий направление колебаний вектора E волны. Расчеты ПЭМВ W предполагают ее определение пятью параметрами: амплитудой E0 , фазой ψ0 , углом поляризации ϖ0 и углами θ0 и ϕ0 . Эти углы определяют направление распространения волны. Дадим определение базовой волны W′ (рис. 2). Ее орты к', p' определяются ортами глобальной прямоугольной системы координат. Для определенности будем полагать, что p' = z, к' = X. Таким образом, волна W′ обладает вертикальной поляризацией и распространяется вдоль оси Ox. Связь ортов волн W и W′ запишем как: (z) (y) (x) v=R (ϕ0)R (θ0)R (ϖ0)v', v≡pˆ,k. В данном выражении R (ф) - матрицы поворота вокруг соответствующих осей, ф - угол поворота; f≡ x, y, z.
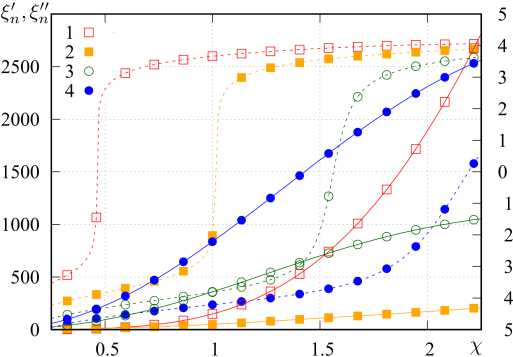
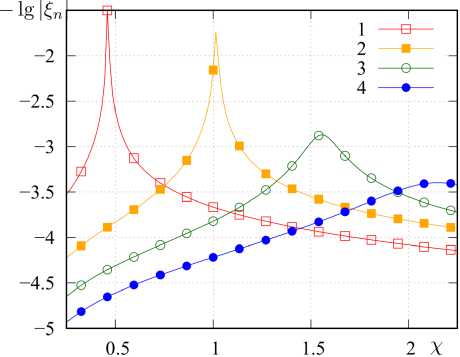
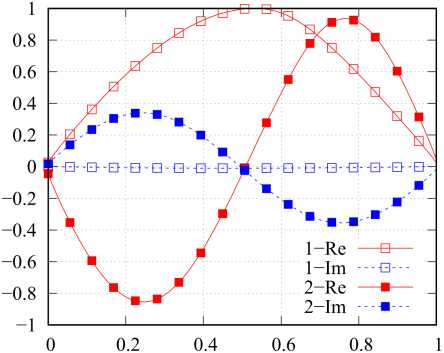
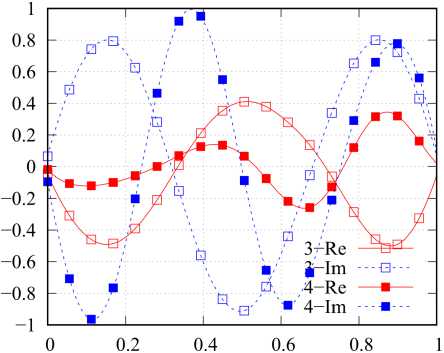
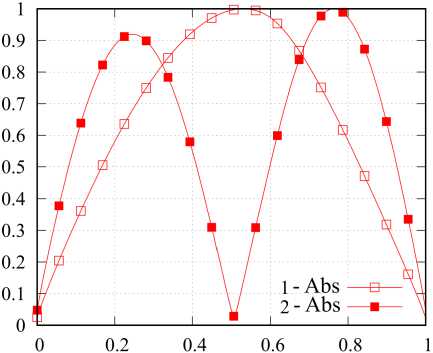
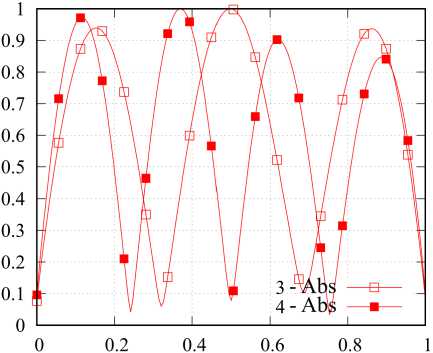
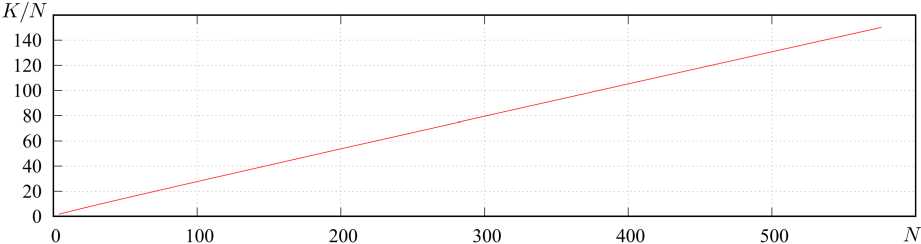
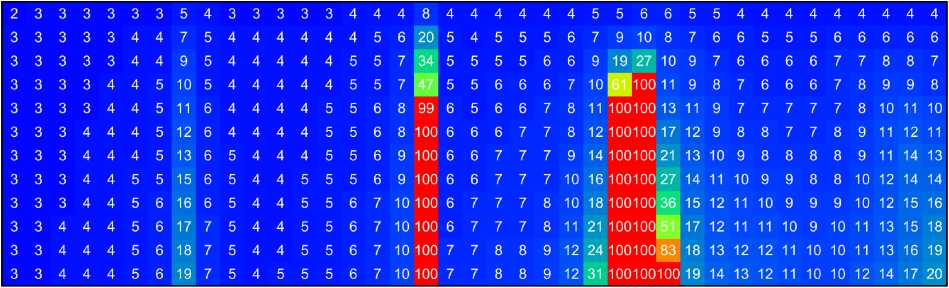
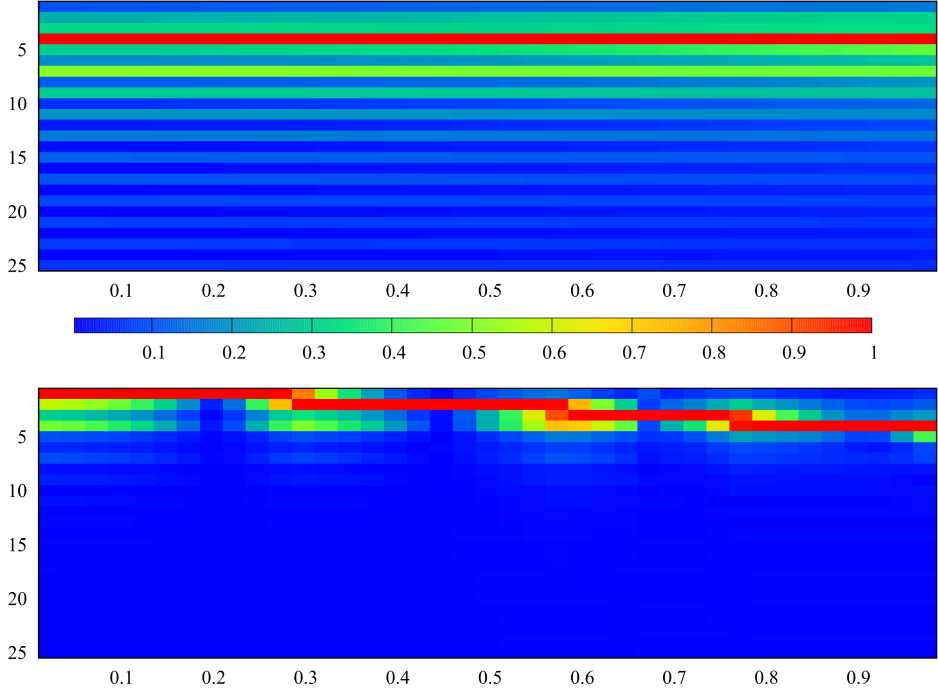
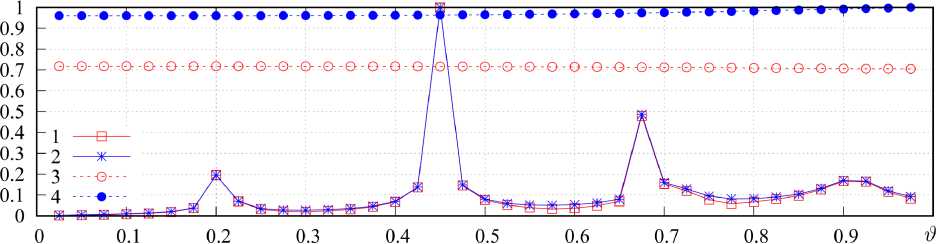
4. Алгоритм расчета массива уникальных матриц В [18] рассмотрены непосредственный и ключевой алгоритмы расчета элементов {p^z)} и {z}. Указанные алгоритмы, в свою очередь, могут быть строгими и приближенными. Достоинством непосредственного алгоритма является универсальность, а основным недостатком - повышенная вычислительная сложность, связанная с необходимостью сравнения блоков матрицы Z. Однако в [18] не было указано, что подобный подход может быть эффективен при расчете на множестве частот и (или) при большом количестве вариантов возбуждения структуры, так как процедура расчета применяется однократно. Для расчета массива уникальных матриц рассматриваемой структуры предлагается использование приближенного комбинированного алгоритма. Суть алгоритма заключается в том, что в качестве информативных параметров in,, in выступают усеченные системы базисных {в}n' = {вq}n‘ и тестовых {Т}n = {тq}n функций (q = qn е Q: 1...Q, q'= qn, е Q': 1.Q'; Q^ Q, Q'^Q'). Ключом к = = κ(ιn, ιn′) в данном случае выступают матрицы собственных и взаимных импедансов небольшой размерности Zn , n , = < Тn , q , У n , n , (вn ,, q, )> . ДлЯ рассматриваемой структуры усеченные СПФ целесообразно строить на основе следующих систем функций: вп(11) = V2cos((2q- 1)nl/(2L)), т„ (l) = вп (1l). (19) n,q n,q n,q Данные системы близки к системе СФ тонкого прямолинейного проводника длиной L при небольших значениях отношений L / X [23]. Вычисления zn n, для рассматриваемой структуры целесообразно проводить в рамках обобщенного метода коллокаций с помощью выражений (9)–(11). Алгоритм расчета состоит из следующих шагов: • для текущих n, n′ на основе информативных параметров ii, ij соответствующих элементов вычисляется ключ к = k(i n, in ‘); • выполняется поиск ключа к’ в {к} удовлетворяющего условию р = | к - к’ | /1 к’ |< р*, где р* - допустимое значение невязки ключей; • если ключ к’ в к-й позиции вектора {к}, удовлетворяет условию р<р*, то p( z), = k; n,n • если ни один ключ к’ е {к} не удовлетворяет условию р < р*, то вектор {к} дополняется ключом к, вектор {z} - матрицей znn,, а pnn, = K', где K′ – число элементов дополненного вектора {к}. 5. Исследование спектральных характеристик матрицы импедансов одиночного спирального элемента Алгоритм выполняется сначала для совпадающих, а затем - для несовпадающих n и n'. На первом этапе определяется число матриц собственных импедансов, а на втором - число ма- триц взаимных импедансов в уникальном массиве матриц. Ранее было показано, что геометрия спирали (рис. 1, б) может быть определена с помощью шести параметров: радиусов нижнего и верхнего оснований rmax и rmin, высоты спирали H, направления ее вращения , числа витков Nl и радиуса спирального проводника s. При известных указанных параметрах по формулам (15) вычисляются коэффициенты hr и hz, входящие в уравнение образующей спирали (14). При исследовании спектральных характеристик матрицы импедансов одиночного спирального элемента целесообразным представляется использование нормированных параметров, где в качестве главного параметра, нормируемого к длине волны X, следует использовать удвоенный максимальный радиус спирали 2rmax, определяющий максимальные габариты одиночного элемента при H <2r . Отношение 2r / X обозначим сим-max max волом <;. При проведении численного моделирования исследовалась спираль, геометрия которой определялась следующими соотношениями: 2 rmin/(2 rmax )=0,3682, H/(2 rmax ) = 0,025, S/(2 rmax ) = = 0,0037, Nl =2, s = 1. При этом L/(2rmax) «4,323, или L / X = х~ 4,323^. Последнее соотношение полезно знать в силу того, что в структурах, подобных рассматриваемым, возникают резонансы трех типов: тонкопроволочные, поверхностые и объемные. Тонкопроволочные резонансы определяются преимущественно длиной и формой проводника, являются высокодобротными и наиболее ярко проявляются при полуцелых значениях х, не превышающих нескольких единиц. Поверхностные резонансы определяются формой поверхности, служащей носителем спирального элемента, объемные резонансы определяются объемом, содержащим спиральный проводник. Резонансы последних двух типов имеют, как правило, существенно более низкую добротность и возникают при кратных значениях волновых размеров структуры, также не превышающих нескольких единиц. При численном моделировании параметр ^ менялся в пределах от 0,0125 до 0,53, при этом χ∈ е [0,054;2,28]. Матрицы импедансов формировались в рамках традиционного метода коллокаций, при этом число сегментов M предполагалось рав- а Рис. 3. Зависимость Sn = Re^n (сплошные кривые, а), У’= sgn(Im(^n)) lg(1+ | Im(^n )|) (штриховые кривые, а) и -lg | ^n | (б) от x; номер маркера (линии) соответствует номеру собственного значения Fig. 3. Dependence tn = Re^n (solid curves, a), ^n = sgn(Im(^n)) lg(1+ | Im(£n )|) (dashed curves, a) and -lg | ^n | (b) from x; marker (line) number corresponds to number eigenvalue б ным 179, что при заданном отношении ε/(2r ) max удовлетворяло условию (12). Здесь и далее волновое сопротивление среды Wm полагалось равным 120π Ом, что справедливо для вакуума или воздушной среды. При этом предполагалось, что среда являлась недиссипативной, поэтому для вычисления волнового числа использовалось выражение k =2π/λ. На рис. 3 представлены зависимости ^n = Re^ n, ^nn = sgn(Im(^n)) lg(1+ IIm(^n)|) (a) и -lg I ^n 1 от χ (б), индекс n соответствует номеру кривой на графиках. Приведенные графики показывают, что зависимость СЧ от частоты имеет резонансный характер, и в рассматриваемом диапазоне мы наблюдаем четыре резонанса. Эти резонансы можно классифицировать как тонкопроволочные вследствие близкого соответствия значениям n/2. При этом графики показывают, что резонанс для первой собственной функции наступает при у, несколько меньшем, чем 1/2, а резонансы для последующих собственных функций возникают для значений χ, больших, чем n /2, причем с ростом n отклонения в большую сторону возрастают. Этот момент можно понять, если представить каждую собственную функцию в виде суперпозиции пары бегущих волн, распространяющихся по проводнику во взаимно противоположных направлениях. В этом случае становится очевидным, что фазовая скорость данных волн для n = 1 будет меньше скорости света, а для n >1 – больше скорости света. Рост фазовой скорости, в свою очередь, связан с увеличением межвиткового взаимодействия, которому способствуют рост χ и особенности форм высших собственных функций. Также здесь мож- но отметить, что добротность резонансов довольно быстро падает с ростом n. На рис. 4 приведен вид первых четырех нормированных собственных функций вn (l / L)/ вnmax, вычисленных при соответствующих резонансных значениях χ. Здесь хорошо видно, что форма собственных функций близка к (19), но при этом общая амплитуда СФ при n >1 имеет существенную мнимую составляющую. Также здесь можно отметить асимметрию форм СФ, возрастающую с ростом n. Очевидно, что данная асимметрия определяется формой спирального элемента. Амплитудные распределения показывают, что СФ представляют собой преимущественно стоячую волну, при этом отличные от нуля значения тока в узлах при n >1 говорят о незначительном присутствии компоненты бегущей волны. Направление распространения данной компоненты на проводнике можно идентифицировать по направлению убывания амплитуды СФ. Таким образом, исследование спектральных характеристик матрицы импедансов одиночного спирального элемента позволяет сделать вывод об обоснованности дальнейшего применения СПФ (19) и оценить резонансные явления, возникающие в элементах метаструктуры. Здесь также можно заметить, что эта оценка имеет приближенный характер, так как резонансные характеристики элемента в достаточно плотной структуре будут отличаться от аналогичных характеристик одиночного элемента. В данном случае можно ожидать изменения добротности резонансов и смещения резонансных частот. а б в Рис. 4. Вид первых четырех нормированных собственных функций вn (l / L)/ вnmax’ вычисленных при соответствующих резонансных значениях х; номера и составляющие собственных функций указаны на графиках Fig. 4. Form of the first four normalized eigenfunctions вn(l / L) / вn max, calculated for the corresponding resonant values x; numbers and components of eigenfunctions are indicated on the charts г 6. Исследование эффективности алгоритма сжатия блочной матрицы и сходимости итерационного процесса При численном моделировании структуры использовались геометрические параметры одиночного элемента, приведенные в предыдущем разделе. Считалось, что все элементы Li i , связанные x, y с одиночным элементом L выражением (17), имеют один и тот же фиксированный угол фi i = ф, x, y который в расчетах полагался равным 0 градусов. Структура возбуждалась ПЭМВ W, ЭМП которой определяется выражениями (18). Амплитуда вектора электрического поля E0 полагалась равной 1 В/м, начальная фаза ψ0 – 0°, угол ϖ0 – 0°, угол поляризации п0 = 90 (H-поляризация); угол падения θ0 принимал значения 0, 45 и 90°. Эти случаи мы будем называть случаями торцевого, бокового и нормального падения ПЭМВ соответственно. Геометрия решетки определяется структуры четырьмя параметрами: расстояниями между соседними узлами решетки hx и hy вдоль соответ- ствующих осей координат и числом элементов Nx, Ny вдоль соответствующих осей. Отношение hx / λ обозначим символом ϑ . При численном моделировании предполагалось, что hx = hy = ha, Nx = Ny = Na. Рассматривались структуры с Na =2,4...24. Общее число элементов N подобных структур определяется как Na. Для рассматриваемой структуры параметры ς и ϑ связаны соотношением д / 3 = 0,53, при этом данное соотношение, по сути, является коэффициентом заполнения структуры элементами. При д / 3 = 1 соседние элементы структуры вплотную примыкают друг к другу. Исследования проводились в диапазоне 3е [0,0625;1]. Сходимость итерационного процесса в нашем случае зависит только от Na и 3. Коэффициент сжатия K / N зависит только от Na. На рис. 5 показан график зависимости коэффициента сжатия K / N от числа элементов структуры N. Видно, что данная зависимость является линейной и может быть приближенно описана функцией K / N « (4/15)N = (4/15)N2. Отметим, что при непосредственном расчете матричных Рис. 5. Зависимость коэффициента сжатия K/ N от числа элементов структуры N Fig. 5. Dependence of the compression ratio K/N on the number of structure elements N Рис. 6. Таблица сходимости итерационного процесса: ось абсцисс - 9, ось ординат - Na, значения в ячейках - число итераций Fig. 6. Convergence table of the iterative process: x-axis - 9, ordinate axis is Na, values in cells are number of iterations элементов данная зависимость является квадратичной. Таким образом, предложенный алгоритм расчета элементов блочной матрицы позволяет существенно сократить затраты машинной памяти и машинного времени. На рис. 6 представлена таблица сходимости итерационного процесса. Максимальное число итераций равно 100. Таким образом, достижение данного значения соответствует отсутствию сходимости итерационного процесса. С учетом указанной ранее связи между переменными σ и χ тонкопроволочные резонансы на одиночных элементах структуры будут возникать при условии 9- 0,217n, в котором n - номер резонанса. В результате для первых четырех собственных функций резонансы должны возникать в окрестности 9 = 0,217, 0,434, 0,651, 0,868. При этом возможны смещения резонансных частот вследствие взаимодействия элементов структуры. Рисунок показывает, что ухудшение и отсутствие сходимости наблюдается в окрестности резонансных частот первых трех собственных функций, при этом первый резонанс не приводит к потере сходимости итерационного процесса, а резонанс четвертой собственной функции себя вообще никак не проявляет. Для более полного объяснения этого эффекта необходим расчет угловых распределений поля каждой СФ с определением пространственной ориентации максимумов поля. 7. Анализ и интерпретация результатов решения внутренней электродинамической задачи Рассмотрим функции сторонних полей и токовые функции, аппроксимируемые разложениями по собственным функциям интегрального оператора одиночного элемента (разложения вида (2)): nn (l) = n’вn,q (l), Zn (l) = ^Eqn’вn,q (l); qq l∈L,Iq(n)∈in,Eq(n)∈en. Для рассматриваемой структуры целесообразно оперировать векторами усредненных по n амплитудных коэффициентов: f(a’ o Fqa’, Fqa’= N^ | Fqn’|, f = i, e, F ^ I, E, n и соответствующими значениями невязок pn’a’ = = | f(a’ - fna’ | /1 f(a’ |; f = i, e. Расчеты показали, что в исследуемом частотном диапазоне для структур с Na =2...24 при углах падения О0 = 0^90° средние значения этих невязок не превышают 0,09, а медианные значения меньше 0,025. Это, с одной стороны, подтверждает целесообразность Рис. 7. Спектрограммы: сверху - e(a/max)(Э), снизу - i(a/max)(3); ось абсцисс - 3, ось ординат - индекс элемента векторов Fig. 7. Spectrograms: top - e(a/max)(3), below - i(a/max)(3); abscissa axis - 3, ordinate axis - index of element of vectors Рис. 8. Зависимости ^.aXup) (кривая 1), ^^up) (кривая 2), e(maXup) (кривая 3) и enmup) (кривая 4) от 3 Fig. 8. Dependencies /Sup) (curve 1), dO/Sup) (curve 2), e^/Sup) (curve 3) and e^а/2ир) (curve 4) from 3 max nrm max nrm рассмотрения усредненных векторов амплитудных коэффициентов, а с другой - говорит о высокой степени однородности токовых функций. Здесь и далее нормированные к максимальному значению векторы амплитудных коэффициентов будем обозначать как f(a/max) = f(a)/fmax. Под fmax будем понимать максимальный амплитудный элемент вектора f, а под fnO^ =| f(a) | - его евклидову норму. Супремумом вектора f(a) будем называть величину f(sup) = max(fax, fnOmm). На рис. 7 сверху представлена нормированная спектрограмма e(a /max)(3) для случая Na =8, Оо =90°. Вдоль оси абсцисс спектрограммы отложены значения 3, вдоль оси ординат - номера элементов вектора e(a/max). Видно, что спектрограмма не зависит от 3, при этом максимальная амплитуда наблюдается для четвертой собственной функции. Это обусловлено тем, что исследуемые спиральные элементы имеют число витков, равное двум. В целом можно отметить, что спектр является довольно широким в исследуемом диапазоне значений 3. На рис. 7 снизу представлена соответствующая нормированная спектрограмма i(a/max)(3) для аналогичного случая, а на рис. 8 - зависимости f • a/sup) = fj(a)(3)/ f(sup) (f = i,e, j = max, nrm). Приведенные зависимости и спектрограмма показывают, что спектр собственных функций для рассматриваемой структуры в исследуемом диапазоне значений 0 является узкополосным и имеет при этом резонансный характер. Разница уровней графиков fO/sUpp и f amOup) (f = i, e) позволяет оценить степень вырожденно-f(a/sup) — f(a/sup) pnpVTn сти спектра. Так, если jmax = Jnrm , то спектр является вырожденным и состоит только из одной спектральной компоненты. Таким образом, спектр стороннего поля является невырожденным во всем исследуемом диапазоне, а спектр токовых функций близок к вырожденному и практически является таковым вблизи резонансных частот, определяющихся резонансными частотами для собственных значений элементов, из которых состоит метаструктура. Данные результаты приобретают очень важное значение с точки зрения анализа метаструктур, так как позволяют использовать в качестве проекционных функций компактный набор собственных функций, имеющих существенные амплитуды в окрестности исследуемой частоты. При этом для метаструктур конечных размеров вполне применимо решение СЛАУ прямыми методами. Наименьший размер матрицы таких СЛАУ будут иметь на резонансных частотах, когда распределение тока по элементам определяется только одной собственной функцией (вырожденные распределения тока). В этом случае полезным в аналитическом плане представляется решение задачи определения собственных векторов метаструктуры, определяющих конечный набор распределений комплексных амплитуд вырожденных распределений токов на элементах. В дальнейшем авторы планируют решить данную задачу и определить характеристики рассеянного поля для рассмотренной структуры в резонансных и нерезонансных случаях. Заключение В статье рассмотрен системный подход к строгому решению внутренней задачи электродинамики для многоэлементных структур. В основе подхода лежит использование итерационных процедур типа Гаусса - Зейделя или Якоби, реализуемых для блочной матрицы СЛАУ, получаемой в рамках метода моментов [15]. Рассмотренный подход предполагает использование априорной информации о структуре для реализации эффективных алгоритмов расчета блочной матрицы СЛАУ [18]. В данной работе показана целесообразность определения спектральных характеристик интегральных операторов внутренней задачи для одиночных элементов, входящих в состав метаструктуры. В результате решения данной задачи производится определение собственных функций и собственных значений интегральных операторов, а также их зависимость от частоты. Информация о собственных функциях дает возможность обоснованно подходить к выбору систем проекционных функций, используемых в рамках метода моментов для формирования блочной матрицы СЛАУ. Информация о частотной зависимости собственных значений позволяет прогнозировать возникновение резонансных явлений, возникающих в многоэлементных структурах. В статье продемонстрировано применение предложенного подхода к решению внутренней задачи для конкретной структуры – регулярной двумерной решетки, состоящей из конических спиральных элементов, возбуждаемой плоской линейно-поляризованной электромагнитной волной. В ходе решения поставленной задачи была выявлена связь между частотной зависимостью собственных чисел интегрального оператора внутренней задачи одиночного элемента, используемого для создания метаструктуры, с резонансными явлениями, возникающими в метаструктуре, а также подтверждена связь резонансных явлений со сходимостью итерационного процесса. Исследован спектр токовых функций элементов метаструктуры. Показано, что амплитудные спектры на различных элементах метаструктуры довольно слабо отличаются друг от друга, что позволяет рассматривать при анализе усредненные амплитудные спектры. Выявлено, что усредненный спектр стороннего поля на элементах является относительно широким, а усредненный спектр токовых функций близок к вырожденному и практически является таковым вблизи резонансных частот. Выявленные особенности позволяют использовать в качестве проекционных функций компактный набор собственных функций, имеющих существенные амплитуды в окрестности исследуемой частоты, что в конечном счете ведет к уменьшению размеров блоков матрицы СЛАУ и существенно упрощает решение внутренней задачи. Представленные результаты еще раз подтверждают эффективность применения итерационного подхода к строгому решению внутренней задачи электродинамики для многоэлементных структур в нерезонансных случаях. Дальнейшее развитие предложенного подхода авторы связывают с введением процедур выявления резонансных явлений и отдельном рассмотрении внутренней задачи в окрестности резонансных частот.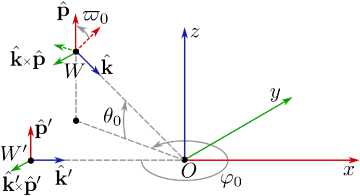

Список литературы Решение внутренней задачи для конечной регулярной двумерной решетки спиральных элементов, возбуждаемой плоской электромагнитной волной
- Неганов В.А., Осипов О.В. Отражающие, волноведущие и излучающие структуры с киральными элементами. М.: Радио и связь, 2006. 280 с.
- Ивченко Е.Л., Поддубный А.Н. Резонансные трехмерные фотонные кристаллы // Физика твердого тела. 2006. Т. 48, № 3. С. 540–547. URL: https://journals.ioffe.ru/articles/3354
- Веселаго В.Г. Электродинамика веществ с одновременно отрицательными значениями ε и μ // Успехи физических наук. 1967. Т. 92, № 3. С. 517–526. DOI: https://doi.org/10.3367/UFNr.0092.196707d.0517
- Pendry J.B. A chiral route to negative refraction // Science. 2004. Vol. 306, no. 5700. P. 1353–1355. DOI: https://doi.org/10.1126/science.1104467
- Composite medium with simultaneously negative permeability and permittivity / D.R. Smith [et al.] // Physical Review Letters. 2000. Vol. 84, no. 18. P. 4184–4187. DOI: https://doi.org/10.1103/PhysRevLett.84.4184
- Extremely low frequency plasmons in metallic mesostructures / J.B. Pendry [et al.] // Physical Review Letters. 1996. Vol. 76, no. 25. P. 4773–4776. DOI: https://doi.org/10.1103/PhysRevLett.76.4773
- Low frequency plasmons in thin-wire structures / J.B. Pendry [et al.] // Journal of Physics: Condensed Matter. 1998. Vol. 10, no. 22. P. 4785–4809. DOI: https://doi.org/10.1088/0953-8984/10/22/007
- Magnetism from conductors and enhanced nonlinear phenomena / J.B. Pendry [et al.] // IEEE Transactions on Microwave Theory and Techniques. 1999. Vol. 47, no. 11. P. 2075–2084. DOI: https://doi.org/10.1109/22.798002
- Вендик И.Б., Вендик О.Г. Метаматериалы и их применение в технике сверхвысоких частот (Обзор) // Журнал технической физики. 2013. Т. 83, № 1. C. 3‒28. URL: https://journals.ioffe.ru/articles/viewPDF/41403
- Schelkunoff S.A., Friis H.T. Antennas Theory and Practice. New York: Wiley, 1952. 672 p.
- Harrington R.F. Field Computation by Moment Method. New York: Macmillan, 1968. 150 p.
- Gallagher R.H. Finite Element Analysis: Fundamentals. Hoboken: Prentice-Hall, 1974. 420 p.
- Кисель В.Н., Лагарьков А.Н. Электродинамические модели тонкослойных метаматериалов и устройства на их основе // Радиотехника и электроника. 2009. Т. 54. № 5. С. 531–540. URL: https://elibrary.ru/item.asp?id=12136589
- Ильинский А.С., Перфилов О.Ю., Самохин А.Б. Итерационный метод решения интегральных уравнений теории проволочных антенн // Математическое моделирование. 1994. Т. 6, № 3. С. 52–59. URL: https://www.mathnet.ru/rus/mm1848
- Неганов В.А., Марсаков И.Ю., Табаков Д.П. Расчет взаимодействия элементов метаструктуры на основе метода Гаусса – Зейделя // Физика волновых процессов и радиотехнические системы. 2013. Т. 16, № 3. C. 6–16. URL: https://elibrary.ru/item.asp?id=21007651
- Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. М.: Лаборатория базовых знаний, 2000. 624 с.
- Неганов В.А., Табаков Д.П. Корректный электродинамический анализ киральных элементов и метаматериалов на основе интегральных представлений электромагнитного поля // Физика волновых процессов и радиотехнические системы. 2014. Т. 17, № 3. С. 29–39. URL: https://journals.ssau.ru/pwp/article/view/7265.
- Табаков Д.П. Применение итерационных процедур к электродинамическому анализу метаматериалов // Радиотехника. 2015. № 7. С. 86–94. URL: https://elibrary.ru/item.asp?id=23837442
- Табаков Д.П., Аль-Нозайли Б.М.А. Расчет токов на многоэлементных излучающих структурах итерационным методом // Радиотехника и электроника. 2022. Т. 67, № 7. С. 651–659. URL: https://elibrary.ru/item.asp?id=48867815
- Драбкин А.Л., Зузенко В.Л., Кислов А.Г. Антенно-фидерные устройства. 2-е изд., доп. и перераб. М.: Сов. радио, 1974. 536 с.
- Табаков Д.П., Аль-Нозайли Б.М.А. Решение внутренней и внешней задач электродинамики для симметричного вибратора с рефлектором из параллельных прямолинейных проводников // Физика волновых процессов и радиотехнические системы. 2024. Т. 27, № 2. С. 7–21. DOI: https://doi.org/10.18469/1810-3189.2024.27.2.7-21
- Табаков Д.П. Об описании излучения и дифракции электромагнитных волн методом собственных функций // Известия вузов. Радиофизика. 2021. Т. 64, № 3. С. 179–191. URL: https://radiophysics.unn.ru/issues/2021/3/179
- Табаков Д.П., Майоров А.Г. Аппроксимация решения внутренней электродинамической задачи для тонкого трубчатого вибратора методом собственных функций // Труды учебных заведений связи. 2019. Т. 5, № 4. С. 58–64. DOI: https://doi.org/10.31854/1813-324X-2019-5-4-58-64
- Интегральное представление электромагнитного поля геометрически киральной структуры / В.А. Капитонов [и др.] // Физика волновых процессов и радиотехнические системы. 2012. Т. 15, № 4. С. 6–13. URL: https://www.elibrary.ru/item.asp?id=19001844
- Вычислительные методы в электродинамике / под ред. Р. Митры; пер с англ. под ред. Э.Л. Бурштейна. М.: Мир, 1977. 487 с.
- Стрижков В.А. Математическое моделирование электродинамических процессов в сложных антенных системах // Математическое моделирование. 1989. Т. 1, № 8. С. 127–138. URL: https://www.mathnet.ru/rus/mm2614


