Решение задач излучения и дифракции электромагнитных волн на основе интегральных представлений электромагнитного поля

Исходными инструментами при решении широкого круга прикладных задач, связанных с излучением и дифракцией электромагнитных волн, а также с исследованием волновых процессов в композитных структурах являются уравнения Максвелла и волновые уравнения. Они имеют различную форму записи и применяются во временной и частотной областях. Отметим, что зачастую прямое их использование (метод конечных разностей [1]) при решении конкретных задач осложнено как в аналитическом плане ввиду сложности получаемых решений, так и в численном – из-за больших вычислительных затрат. Повышение эффективности прямых методов связано с уменьшением области решения, правильным выбором расчетной сетки, применением идеальных согласованных слоев и т. д.

При исследовании структур в неограниченном пространстве более эффективны непрямые методы. Их основу составляет определенная ключевая задача с известным аналитическим решением (функция Грина, [2]). С учетом линейности уравнений электродинамики исходная задача решается посредством декомпозиции структуры до простейших элементов, решение для которых известно, и последующей суперпозиции этих решений.

Данная идея нашла свое воплощение в рамках метода векторных потенциалов [3]. На основе этого метода не представляет особого труда получение простейших форм интегральных представлений электромагнитного поля (ИП ЭМП). Таким образом, метод ИП ЭМП можно считать развитием метода векторных потенциалов. ИП ЭМП связывают ЭМП в любой точке пространства с токами (источниками), находящимися в заданном объеме, поэтому для решения внешней задачи необходимо знать только распределение источников, что существенно снижает ее размерность в сравнении с непосредственным применением уравнений Максвелла либо волновых уравнений. При рассмотрении области источников совместно с условиями на границах раздела сред из ИП ЭМП естественным образом формируются системы интегральных уравнений (ИУ) относительно неизвестных распределений источников (внутренняя задача электродинамики). На основе общих ИП ЭМП можно получить усложненные формы, которые в явном виде учитывают особенности поведения полей вблизи и на поверхности излучающих и пе-реизлучающих структур, а также особенности их геометрии (симметрии различных видов, наличие геометрических сингулярностей и т. д.). Можно отметить, что дополнительная информация о рассматриваемой структуре и о задаче в целом позво-

LM^^e © Табаков Д.П., Морозов С.В., 2020

ляет существенно упростить ее решение на основе ИП ЭМП.

В настоящей статье приведены примеры использования метода ИП ЭМП при решении электродинамических задач. Приведены полученные авторами новые и ранее опубликованные результаты для конкретных структур.

1. Общие формы ИП ЭМП

«Классические» ИП ЭМП . Рассмотрим некоторые виды ИП ЭМП, приняв за исходную точку метод векторных потенциалов. Электрический A ^{( e )} и магнитный A ^{( m )} векторные потенциалы могут быть записаны в виде

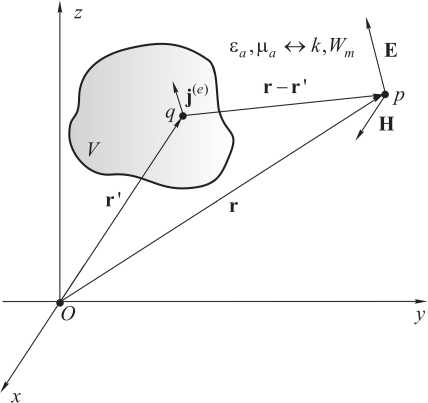
Рис. 1. К решению задач в неограниченном пространстве

Fig. 1. To solving problems in unlimited space

A ( i ) = j GdV , i = e , m , V

где G = G(r,r') - функция Грина, r - радиус-вектор, проведенный в точку наблюдения p, r' - радиус-вектор, проведенный в точку источника q, j(i) = j(i)(r') - вектор объемной плотности электрического или магнитного тока (источники). Источники расположены в объеме V, по которому производится интегрирование (рис. 1). Выражения (1), дополненные выражениями

E=M(Wm A( e ),A(m)), m                                                 (2)

H = M ( W_m ¹A ^{( m} ) ,- A ⁽ e ) ), представляют собой инструмент, называемый методом векторных потенциалов. Здесь

M ( U , V ) = ( k ² U + V- ( V- U )) / ik - V x V ,

– векторный дифференциальный оператор, k – волновое число среды, W_m - ее волновое сопротивление. Совокупность выражений (1) и (2) можно считать одной из форм интегро-дифференциальных представлений электромагнитного поля (ИДП ЭМП). Этим выражениям можно поставить в соответствие следующую запись:

E ( r ) = M ( W _m j ⁽ e ) , j ^{( m} ) ) GdV ;

^{V m}                                        (3)

H ( r ) = Jy M ( W m j ^{( m} ) , - j ⁽ e ) ) GdV .

В отличие от (2), в (3) дифференциальные операторы применяются к источникам поля. В обоих случаях максимальный порядок дифференцирования равен двум. Выражения (3) назовем классическим ИП ЭМП. Укажем пару негативных моментов, связанных с ним. Первый момент - присутствие значительного числа дифференциальных операторов, которые существенно усложняют аналитические выводы ИП ЭМП конкретных структур в системах координат, отличных от декартовой. Второй момент – наличие неявных особенностей различного типа в ядрах интегральных операторов при r ^ r'. Это ведет к проблемам при решении внутренней электродинамической задачи и при определении ближних полей структур, особенно в окрестности геометрических сингулярностей.

ИП ЭМП общего вида . Указанные проблемы можно устранить с помощью дополнительных аналитических преобразований в (1), (2). Так, можно получить интегро-дифференциальное ( L 1 = L 1 ) и интегральное ( L 1 = L 1 ) представления вида

E ( r ) = Wik m L 1 ( r , r ', j ⁽ e ) ) - L 2 ( r , r ', j ^{( m} ) );

W ^{- 1}

H(r) = m- L1( r, r', j(m)) + L2 (r, r', j( e)), где

L '^f ( j k ² G - ( V j ) d B)dV ,

V

L-^f ( j C - ( j - d ) d D)dV ,

V

L 2 = J^ B ( d x j ) dV

- интегральные операторы; G , B , C , D - ядра интегральных представлений, являющиеся функциями r и r '; d = r - r ' - вектор, проведенный из точки источника в точку наблюдения. Как можно видеть, приведенные интегральные представления практически не содержат дифференциальных операторов, только в (4) необходимо определить дивергенцию от j .

Еще одним важным достоинством приведенных ИП ЭМП является возможность легкого выде-

а

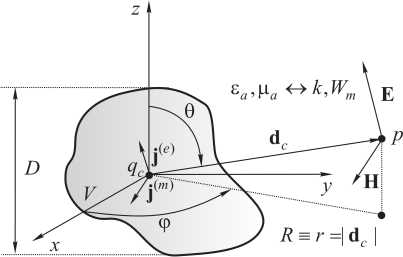
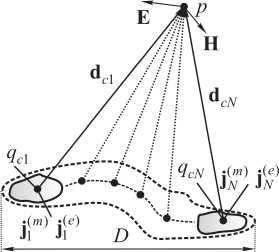
Рис. 2. Дальняя зона излучающих структур: a - представление в случае одного фазового центра; б - представление в случае множества фазовых центров

Fig. 2. Far zone of emitting structures: a – representation in the case of one phase center; b – representation in the case of many phase centers

б

ления особенностей поведения ядер. Так, любую компоненту ядра можно представить в виде разностной (регулярной) F r и асимптотической (сингулярной) F_a частей: F = F_r + F_a ,

F_r = F - F_a ,                                            (5)

F ≡ G , B , C , D .

Сингулярная часть определяется как асимптотика F при r ^ r '. Предполагается, что интегрирование по ней можно осуществить аналитически. Приведенные выражения, дополненные (5), можно назвать сингулярными ИП ЭМП.

ИП ЭМП дальней зоны . Рассмотрим дальнюю зону излучающих и переизлучающих структур, имеющую важное значение при решении задач излучения и дифракции. В [4] показано, что на основе (4) несложно получить ИП ЭМП для расчета дальней зоны:

E ( r ) = L , ( r , r c , r ', W_m j ⁽ e ) , j ⁽ m ) );

H ( r ) = L , ( r , r c , r ', W ^ - j m ⁾ , - j ⁽ e ) );

здесь

^L , = — ikG f [ j ⁽ i ) - ( j ⁽ i ) ■ d о c ) d o c + d о c x j j ] PdV V

– асимптотический интегральный оператор, G = G ( r , r c ) - функция Грина, записанная относительно фазового центра в точке q c , r c - радиус-вектор, проведенный в фазовый центр, множитель

P = P(r, rc, r') = exp(ikd0c ■ (r' - rc)), d0c=d0(r,rc)=(r-rc)/|r-rc| учитывает разность фаз между различными излучающими точками на структуре, d0c – единичный вектор, направленный из фазового центра qc в точку наблюдения p (рис. 2, а). ИП ЭМП (6) свободно от недостатков традиционно используемых для этих целей выражений [5] (привязка к сферической системе координат, совмещение фазового центра с началом координат и его единственность, завышенная граница начала дальней зоны r > 2D2 / X, где D - размер излучающей системы). Полученные выражения легко обобщаются на случай произвольного числа фазовых центров qci (рис. 2, б) с помощью принципа суперпозиции:

E ( r ) = £ l _w ( r , r ci , r ', W_m j e ) , j ⁽ m ) );

ⁱ                                                                       (7)

H ( r ) = V i ( r , r ci , r ', W -1 j ⁽ m ) , - j ⁽ e ) ).

i

Таким образом, полученные выражения обладают инвариантностью по отношению к выбору системы координат и возможностью учета произвольного числа фазовых центров. Последнее обстоятельство является особенно важным с точки зрения расчетов сложных излучающих структур, т. к. граница дальней зоны оценивается уже выражением r > 2d2 / X, где d - наибольший раз-max          max мер элемента в излучающей системе, а не полный размер системы D. Это открывает путь к построению эффективных алгоритмов расчета сложных антенн, антенных решеток и метаструктур.

ИП ЭМП квазиодномерных структур . Под ква-зиодномерными (КОС) будем понимать структуры, имеющие продольный размер L , соизмеримый или много больший длины волны X , и регулярное поперечное сечение, длина контура C которого много меньше L и много меньше или соизмерима с длиной волны λ (рис. 3). К КОС можно отнести трубчатую структуру, плоскую полосковую структуру, полосковую структуру в слое малой электрической толщины и т. д.

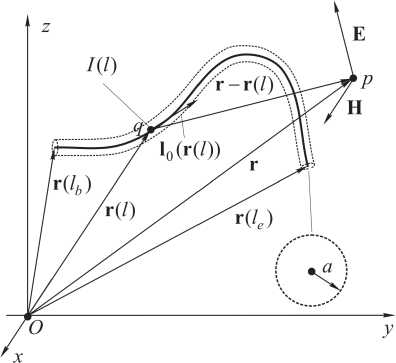
Рис. 3. Геометрия квазиодномерных структур

Fig. 3. Geometry of quasi-one-dimensional structures

Все КОС можно разделить на электрические и магнитные. У электрической КОС поверхность S обладает бесконечно большой электрической проводимостью a e , на ней возможны электрические токи j ⁽ e ) . У магнитной КОС S имеет бесконечно большую магнитную проводимость σ ^m , и на ней возможны магнитные токи j ^{( m} ) . Выражения для магнитных КОС получаются из выражений для электрических КОС с помощью замены, вытекающей из принципа двойственности:

H→-E; E→H; Wm→1/Wm, поэтому приведем ИП ЭМП только для электрических КОС. Объединяющим фактором геометрии КОС является уравнение образующей. Под L будем понимать образующую или множество точек образующей. Будем считать, что кривая L – простая (без самопересечений) и не содержит особых точек, а радиус-вектор r(1) имеет непрерывные первую и вторую производные. Поверхность S структуры строится на основе уравнений образующей.

ИП ЭМП трубчатой КОС можно записать следующим образом:

∞

F ( r ) = У J L I m ‘ ( ¹ '^)К п ?( r , ¹^ ;

m ‘ = -да

F = E, H, f = e , h ,

здесь l ′ – натуральный параметр на образующей L , I_m – азимутальные гармоники поверхностной плотности тока n в силу условий L ^ a , где a -радиус трубки, и L ^ X , имеющей только продольную составляющую n ( ⁵ ) = l o ( 1 ) *П 1 ( ⁵ ), для которой

1 ^∞

П ; ⁽ V , ¹ ) =       У I m ^{( 1} ) exp( - im v ),

2 п a m=-да

ψ – азимутальная координата на поверхности трубки, l ₀ ( l ) – единичный вектор касательной на образующей. Так как a ^ X , то данный ряд является быстро сходящимся. Гармоника I ( l ) = I ( l ) описывает распределение полного тока ⁰                                                 ( f )

по длине L структуры, Km′ – ядра интегральных представлений. Радиус-вектор поверхности трубчатой структуры записывается как r(s)=r(l)+a⋅ρ0(s), р0 (v, 1) = n 0 (1) cos( v) - b0 (1) sin( v).

Здесь P o ( v , 1 ) — радиальный орт локальной цилиндрической системы координат, П о ( 1 ), b o ( 1 ) -единичные векторы нормали и бинормали, построенные в конкретной точке образующей. Предполагается, что при любых значениях 1 радиус а много меньше радиуса кривизны р ( 1 ). Простейшей трубчатой структурой можно считать трубчатый вибратор, интегральные представления для которого приведены в [5].

Тонкопроволочные ИП ЭМП . Известно, что многие структуры можно рассматривать в тонкопроволочном приближении, суть которого заключается в замене провода на нить с током и постановке граничного условия для продольной составляющей поля на поверхности провода. ИП ЭМП для расчета структур в тонкопроволочном легко получается из ИП ЭМП трубчатой структуры, в котором учитывается только нулевая гармоника тока I о ( 1 ) = I ( 1 ), r ( 5 ) заменяется на r ( 1 ), а расстояние вычисляется по приближенной формуле

R = | r - r ( 1 )|² + а ².

Таким образом, ИП ЭМП в тонкопроволочном приближении имеет вид

F ( r ) = J I ( 1 ' ) K F ( r , r ( 1 )) d1' , F = E , H ;                      (9)

здесь K _a – ядра интегральных представлений.

ИП ЭМП поверхностей вращения . Также из (4) можно получить ИП ЭМП для поверхностей вращения (рис. 4). Предполагая, что осью вращения является ось Oz и j ^{( m} ) = 0, вводя азимутальные Фурье-гармоники ЭМП e _m ( r ), h _m ( r ) и Фурье-гармоники поверхностной плотности тока n _m (^r), можно записать:

^e m ^{( r} ) = J.n m ^(r ’ ) z m ^{) ( r} , ^r ' ^{) d1} ,

^L                                                 (10)

h m ⁽ r ^{) =} J ^ m ⁽ r ’ ^{) Z} m ^{) (} r , r ’ ^{) d1} ,

L

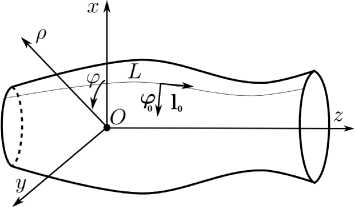
Рис. 4. Поверхность с симметрией вращения

Fig. 4. Surface with rotational symmetry где z^) - тензорные ядра ИП для электрического (i = e) или магнитного (i = m) поля. Интегрирование осуществляется по образующей L поверхности вращения, r = Роx + Zoz - радиус-вектор на образующей.

Проекционные ИП ЭМП . Во всех приведенных ранее ИП ЭМП можно использовать представление источников в виде разложений по проекционным векторным функциям Ф ^ ( r ), определенным в V : j ^{( i )}( r )= ∑ Φ _k ^{( i )}( r ), i ≡ e , h .                                 (11)

k

Такой подход приводит нас к соответствующим проекционным ИП ЭМП. Оптимальный выбор функций 0 ^ ( r ) является самостоятельной и довольно сложной задачей, при решении которой следует опираться прежде всего на геометрию рассматриваемой структуры с учетом возможного наличия у нее различных видов симметрий. Можно утверждать, что наилучшим выбором будет использование собственных функций структуры, так как при этом решение внутренней электродинамической задачи в рамках метода моментов [6] будет наиболее простым.

2.    Излучение электромагнитных волн

Рассмотрим некоторые задачи, связанные с излучением ЭМВ. Инженерный подход к антенным задачам обычно сильно упрощен и зачастую опирается на приближенные распределения токов по структуре. При этом возникает некорректность расчета ближних полей и отсутствует предельный переход от поля в ближней зоне антенны к токам на ее элементах, а также невыполнение граничных условий на элементах структуры. В настоящее время для решения подобных задач все чаще используют системы автоматизированного проектирования (САПР). Но здесь также возникает ряд проблем, среди которых отметим высокие требования к вычислительным ресурсам, высокую сто-

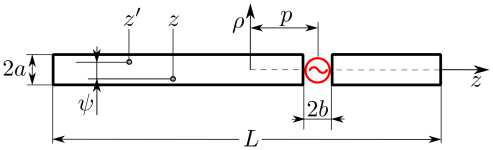
Рис. 5. Геометрия трубчатого вибратора

Fig. 5. Geometry of the tubular vibrator имость САПР, а также ориентацию на численный, а не аналитический расчет, что является негативным моментом в плане интерпретации и прогнозирования получаемых результатов. Рассмотрим некоторые структуры, анализ которых выполнен на основе ИП ЭМП.

Трубчатый электрический вибратор . Трубчатая модель (рис. 5) представляет собой один из вариантов физически корректных моделей электрического вибратора [7]. В целом можно отметить, что данная структура является одной из наиболее изученных в теории антенн и ей посвящено огромное количество работ, при этом большинство работ отвечают на вопросы: «как излучает вибратор?» и «каково распределение тока по вибратору?». Более интересным, на наш взгляд, является вопрос «почему?». То же самое касается и анализа других видов излучающих и переизлуча-ющих структур, однако электрический вибратор является наиболее ярким и простым примером. В [4] приведены сингулярное ИП ЭМП вибратора, соответствующее сингулярное ИУ, а также результаты расчета токов и ближнего поля в рамках корректной и некорректной моделей вибратора.

В последующих работах было принято решение об углублении исследований внутренней задачи для электрического вибратора и исследовании собственных функций интегрального оператора (ИО) соответствующего сингулярного ИУ. Информация о собственных значениях и собственных функциях дает существенные преимущества при анализе структур. Строгий электродинамический анализ излучающих и переизлучающих структур с использованием проекционных ИП ЭМП, при котором проекционные функции являются собственными функциями ИО, возникающего при решении внутренней задачи, мы для краткости будем называть методом собственных функций (МСФ). Данный метод в полной мере отвечает на поставленный ранее вопрос «почему?». Близкий подход был развит в работах [8; 9] (метод характеристических мод).

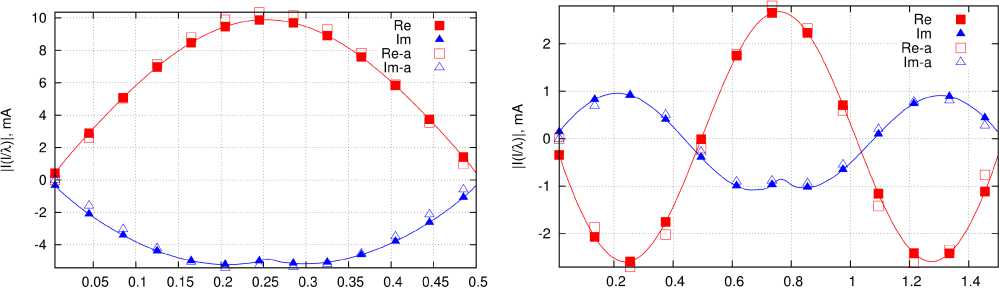
I/X                                                                                                              l/X a                                                   б

Рис. 6. Сравнение решения внутренней задачи (Re, Im) с решением, полученным для аппроксимированных собственных функций (Re-a, Im-a): a - L I X = 0,5; б - L / X = 1,5

Fig. 6. Comparison of the solution to the internal problem (Re, Im) with the solution obtained for the approximated eigenfunctions (Re-a, Im-a): a - L / X = 0,5; b - L / X = 1,5

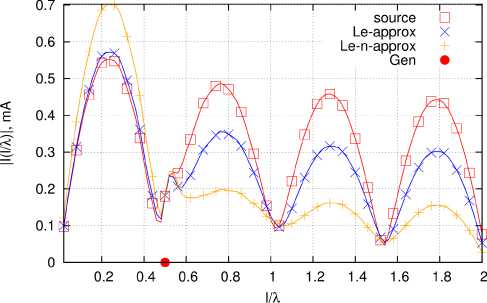
a

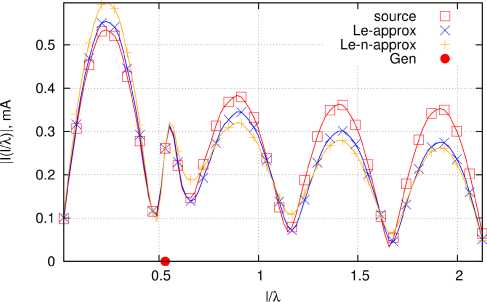
Рис. 7. Экстраполяция решения внутренней задачи при различных значениях L / X ; source - непосредственное решение, Le-approx - аппроксимация зависимостей § k ( L / X ) по L / X , Le-n - полная аппроксимация зависимостей § k ( L / X ); Gen - позиция генератора: а - L / X = 0,5 = 2,125; б - L / X = 0,5 = 2,250

Fig. 7. Extrapolation of the solution to the internal problem at different values L / X ; source - direct solution, Le-approx - approximation of the dependences § _k ( LI X ) in L I X , Le-n - full approximation of the dependences § _k ( LI X ); Gen - position of the generator: a - L / X = 0,5 = 2,125; b - L I X = 0,5 = 2,250

б

Собственные функции φ _k ( l ) и собственные значения § k , полученные данным методом для случая тонкого трубчатого вибратора, были исследованы в работе [10]. Аппроксимация собственных векторов и частотных зависимостей собственных значений продемонстрирована в работе [11]. Здесь было сделано предположение о том, что собственные функции тонкого вибратора в первом приближении допускают достаточно простую тригонометрическую аппроксимацию. Данное предположение было подтверждено результатами аппроксимации распределения полного тока на симметричном вибраторе, полученными при L / X = 0,5 и L / X = 1,5 (рис. 6).

Интересным моментом является оценка экстраполяционных свойств представленных в [11] алгоритмов аппроксимации решения внутренней задачи. Соответствующие результаты для несимметричного вибратора показаны на рис. 7. Как видно из рис. 6 и 7, результат аппроксимации остается вполне приемлемым даже при значениях L / X, почти в 1,5 раза превышающих верхнюю границу зоны аппроксимации. При этом наибольшие расхождения по амплитуде обнаруживаются в окрестности резонанса, наблюдающегося при L / X ® 2. Таким образом, если учесть данный факт при выборе средней точки аппроксимируемой полосы частот, погрешность аппроксимации можно дополнительно уменьшить.

Эллиптическая спиральная антенна. Рассмотрим двузаходную эллиптическую спиральную антенну, расположенную над бесконечно протяженным идеальным металлическим экраном (рис. 8).

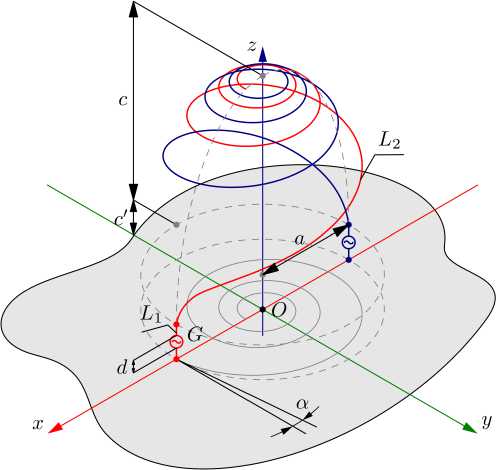
Рис. 8. Многозаходная эллиптическая спиральная антенна

Fig. 8. Multipath elliptical helical antenna

Здесь c’ - смещение эллипсоида вдоль оси Oz , N - число витков спирали, а - угол намотки плоской спирали, являющейся проекцией L ^ на xOy ; a и c – полуоси эллипсоида. Решение внутренней задачи для данной структуры можно существенно упростить, используя двойную симметрию структуры. Первая симметрия связана с учетом экрана в рамках метода зеркальных отображений. Вторая симметрия является поворотной: вторую ветвь спирали в верхнем полупространстве можно получить поворотом основной группы проводников L = L i u L 2 ( L 1 - активный вибратор, L 2 - эллиптическая спираль). В центре L i имеется разрыв длиной d ^ X , содержащий генератор G , создающий напряженность электрического поля E ^{( ext )}, касательная компонента E_l ^{( ext )} которой на образующих проводников отлична от нуля только в области зазора. С учетом (9) ИП ЭМП для рассматриваемой структуры принимает вид

F(r) = ПЛ'-' (1 '*' F’( r, r'm-r;«Ml', m,r L                                                 (12)

F = E , H .

Здесь m = 1... 2 - индекс элемента по зеркальной симметрии ( m -группа), r = 1... R - индекс элемента по поворотной симметрии ( r – группа, R – число поворотов), I_mr ( l ) – функция распределения тока на L ,

ˆˆ r m,r = r m,r(l ) = MmRrr(l ), l‘ e L

- уравнение образующей L_mr , r ( l ') - уравнение для L ;

1 0

M m = 0 1     0

0 0 (-1)( m-1) V cos ar   sin аr 0

R _r = - sin a _r cos a _r 0

0        01

VJ

- матрицы отражения и поворота соответственно, a _r =2 п ( r - 1)/ R. Элементы с одинаковыми индексами в разных группах являются подобными с единичным коэффициентом подобия, поэтому в (12) L = L_m , _r .

Для данной структуры из (12) с учетом приближенного граничного условия на образующей идеального проводника можно получить совокупность независимых систем интегральных уравнений Фредгольма первого рода:

E m,xt ) ( l ) = J L i m , г ( l ') !K m , r ( l , l'^dl ', l e L. (13)

Здесь K_mr ( l , l ') и E^m Xt ) ( l ) - ядра и правые части независимых систем соответственно. После определения из (13) неизвестных амплитуд I_{m r} ток на L вычисляется по формуле

I m , r ( l )=

2 N

П I , ,( l )( — 1) ( m - 1)( m ‘- 1) e 2 п ( r - 1)( r '-1)/ R . m ', r ‘

Полагая R = 2, получаем проводники, необходимые для расчета рассматриваемой структуры. С учетом металлического экрана и противофаз-

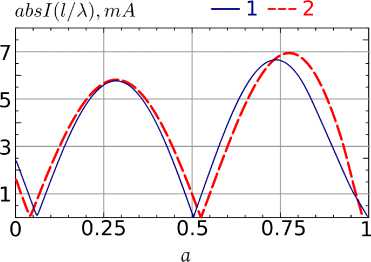
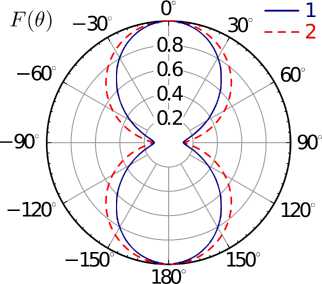
Рис. 9. Результаты расчета модуля распределения тока для a / X = 0,075 ( a ) и a / X = 0, 7 ( б): 1 - FEKO, 2 - ИП ЭМП

Fig. 9. The results of calculating the current distribution module for a / X = 0,075 ( a ) and a / X = 0,7 ( b ): 1 - FEKO, 2 - IP EMF

а

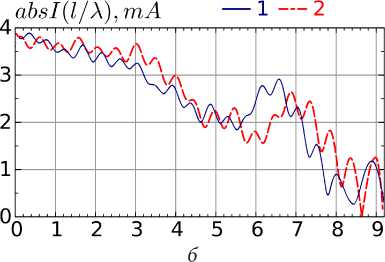
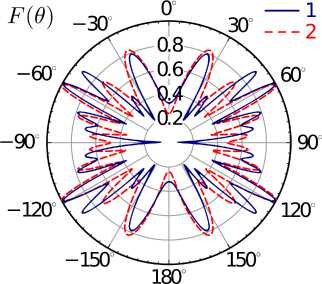
Рис. 10. Результаты расчета модуля распределения тока для a / X = 0,075 ( a ) и a / X = 0,7 ( б): 1 - FEKO, 2 - ИП ЭМП

Fig. 10. Results of calculating the modulus of current distribution for a / X = 0,075 ( a ) and a / X = 0,7 ( b ): 1 - FEKO, 2 - IP EMF

б

ного возбуждения спиралей в (13) необходимо решить только одно ИУ с т = 1, r = 1, что существенно сокращает время расчета. На рис. 9 и 10 показано сравнение численных результатов, полученных в САПР FEKO, с результатами, полученными на основе ИП ЭМП. Основные параметры моделирования: c¹ / a = 0,35, c / a = 4,0, a = 5 ° , N l =4,5.

Из представленных рисунков можно сделать вывод о хорошем совпадении результатов.

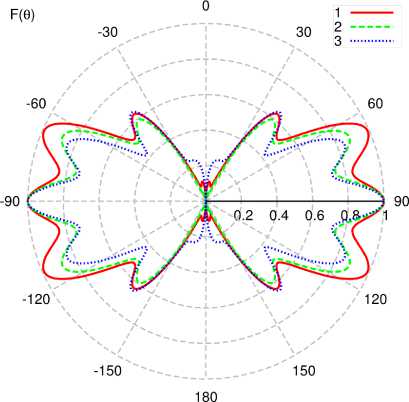
Фрактальная антенна. В настоящее время разработчики технических средств, следуя опыту природы, конструируют антенные системы, используя фрактальный принцип самоподобия. Вполне очевидным становится тот факт, что сложность геометрии фрактальных антенн делает практически невозможным их эмпирический анализ, т. к. наличие большого числа изгибов и близко расположенных взаимодействующих элементов существенно влияет на распределение тока, и уже трудно сказать, какой характер оно имеет. Также затрудняется анализ вторичных характеристик антенн, таких как диаграмма направленности или входное сопротивление. Поэтому здесь метод ана- лиза на основе ИП ЭМП становится практически единственно возможным. В [4] были представлены результаты расчета входного сопротивления излучателя в виде кривой Мура с использованием тонкопроволочных ИП ЭМП. В [12] на основе тонкопроволочных ИП ЭМП были решены внутренняя и внешняя электродинамические задачи для фрактальной антенны Серпинского (ФА) в сравнении с широкополосным вибратором аналогичных размеров. Показано, что у ФА наблюдается свойство повторяемости формы меридианных ДН на частотах, связанных октавным соотношением (рис. 11, L – высота треугольника).

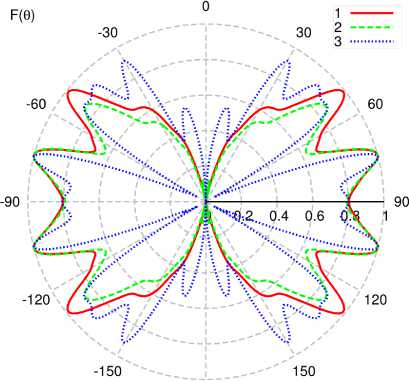
Данное свойство исчезает при больших отношениях L / X для ФА, полученных с помощью малого числа итераций (рис. 11, б ). В дальнейшем разработанный алгоритм расчета был использован при анализе устойчивости решения внутренней задачи при наличии отклонений от идеальной геометрии для антенны Серпинского. Результаты показаны на рис. 12. Здесь h – высота треугольной ячейки, А - максимальное отклонение узлов ячейки. Как и ожидалось, наибольшие отклонения в ДН возникают на более высоких частотах, но в целом распределения тока показали высокую устойчивость к отклонениям геометрии ФА.

а

б

Рис. 11. Результаты расчета меридианной ДН ( ф = 0) фрактальных вибраторов, полученных различным числом итераций: 1 - 6 итераций, 2 - 7 итераций, 3 - 5 итераций; а - L = 4 1 ; б - L = 8 1

Fig. 11. The results of calculating the meridian RP ( ф = 0) of fractal vibrators obtained with a different number of iterations: 1 - 6 iterations, 2 - 7 iterations, 3 - 5 iterations; a - L = 4 1 ; b - L = 8 1

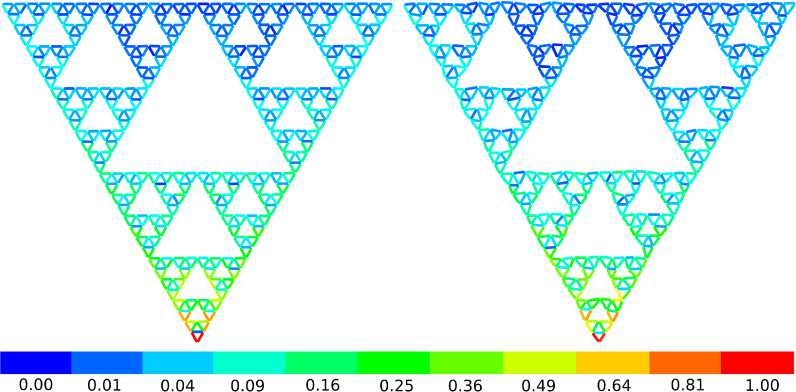
Рис. 12. Расчет распределений тока на ФА (5 итераций) при наличии отклонений в узлах: слева - А = 0,032 h , справа - А = 0,16 h ; L =8 λ

Fig. 12. Calculation of current distributions on the FA (5 iterations) in the presence of deviations in the nodes: on the left - А = 0,032 h, on the right - А = 0,16 h ; L = 8 1

3.    Дифракция электромагнитных волн на одиночных структурах

Необходимость вычисления рассеянного электромагнитного поля часто возникает в прикладных задачах электродинамики, имеющих широкую сферу применения. Так, например, при малых размерах облучателя параболической антенны внутренняя электродинамическая задача для нее может быть сведена к решению задачи дифракции ПЭМВ на параболическом рефлекторе (рис. 13), результаты решения которой представлены в [4]. В [13] рассмотрена задача дифракции для метки радиочастотной идентификации, геометрия

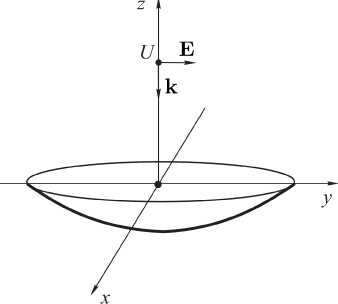
Рис. 13. Падение плоской электромагнитной волны на параболический рефлектор

Fig. 13. The incidence of a plane electromagnetic wave on a parabolic reflector

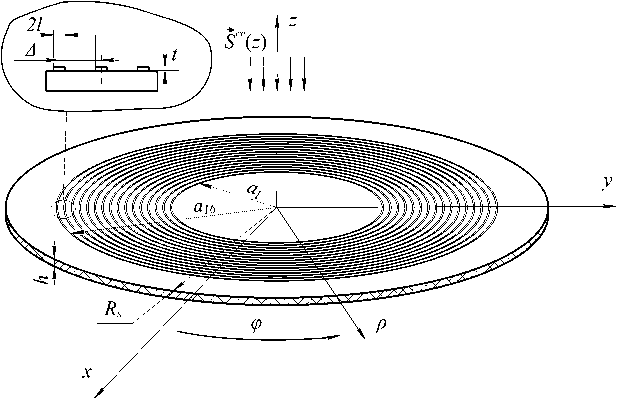
Рис. 14. Общая геометрия задачи

Fig. 14. General geometry of the problem

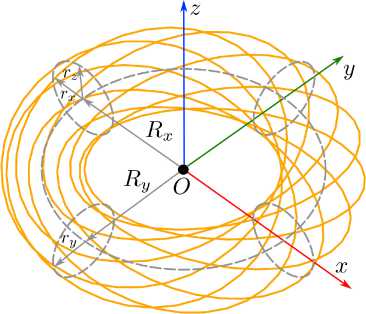
Рис. 15. Геометрия многовитковой киральной рамки

Fig. 15. Geometry of the multiturn chiral frame

которой показана на рис. 14. Решение задач в [4; 13] осуществлялось на основе ИП ЭМП для поверхностей с симметрией вращения.

В [14] приведены результаты, полученные с помощью тонкопроволочных ИП ЭМП для геометрически киральной структуры [15], состоящей из совокупности разомкнутых колец, а также для простой и совмещенной цилиндрической спиралей. Показано, что, несмотря на схожую геометрию, спирали совершенно по-разному ведут себя в одинаковых условиях возбуждения токов. В целом можно отметить, что строгие математические модели базовых элементов, использующихся для создания метаматериалов, частным случаем которых можно считать киральные структуры, могут быть легко получены на основе тонкопроволочных ИП ЭМП. В данной работе одним из авторов (Табаков Д.П.) впервые предлагается математическая модель нового базового элемента - много-витковой киральной рамки (МКР). МКР также может рассматриваться в качестве самостоятель- ной излучающей структуры либо как компонент антенных решеток. Особенностью МКР является значительная длина проводника, что в сочетании с его замкнутостью может создавать предпосылки для появления интересных эффектов в построенных на основе МКР метаструктурах.

Геометрия МКР представлена на рис. 15. Она состоит из единственного проводника L , радиус которого равен в . Уравнения образующей проводника МКР имеют вид:

L : r ( t ) = x ₀ X ( t ) + y ₀ Y ( t ) + z ₀ Z ( t ), t ∈ [0;2 π ];

X ( t ) = r_x sin( t ) + R_x sin(( N - 1) t );

Y ( t ) = r_y cos( t ) - R_y cos(( N - 1) t );

Z ( t ) = r_z sin( sNt ).

Здесь X , Y , Z = f ( t ) – параметрические функции; R_x , R_y – полуоси эллипса, являющегося усредненной образующей рамки; r_x , r_y , r_z – полуоси эллипсов, ограничивающих область с проводником L ; N – число витков проводника, s = ± 1 – вариант закрутки проводника (правая и левая рамки), t – параметр. Таким образом, геометрия МКР определяется семью параметрами, что дает широкие возможности в плане ее модификации.

На основе тонкопроволочного интегрального представления электромагнитного поля была построена строгая математическая модель МКР. Рассмотрена задача дифракции плоской электромагнитной волны (ПЭМВ) на структуре. Для случая нормального падения ПЭМВ, поляризованной вдоль оси OX, при различных отношениях R / λ проведено предварительное численное моделирование кольцевой МКР (Rx = Ry = R, X - длина

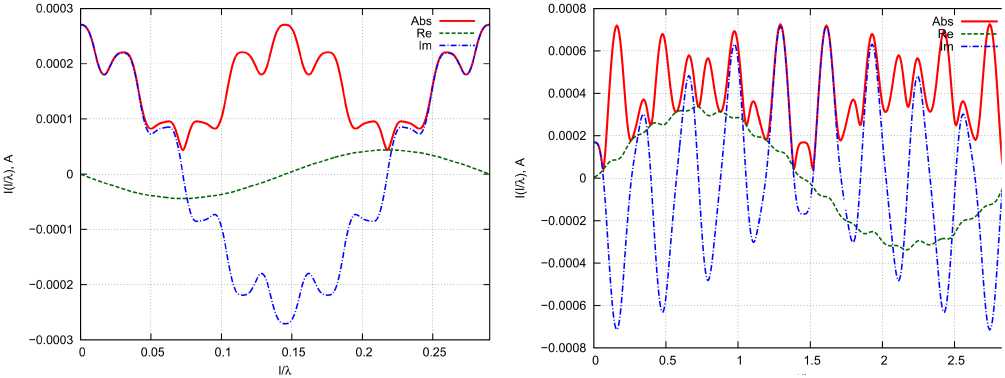
б

а

Рис. 16. Комплексные распределения полного тока вдоль проводника спирали для случаев R / X = 0,005 ( а ) и R / X = 0,05 ( б)

Fig. 16. Complex distributions of the total current along the spiral conductor for the cases R / X = 0,005 ( a ) and R / X = 0,05 ( b )

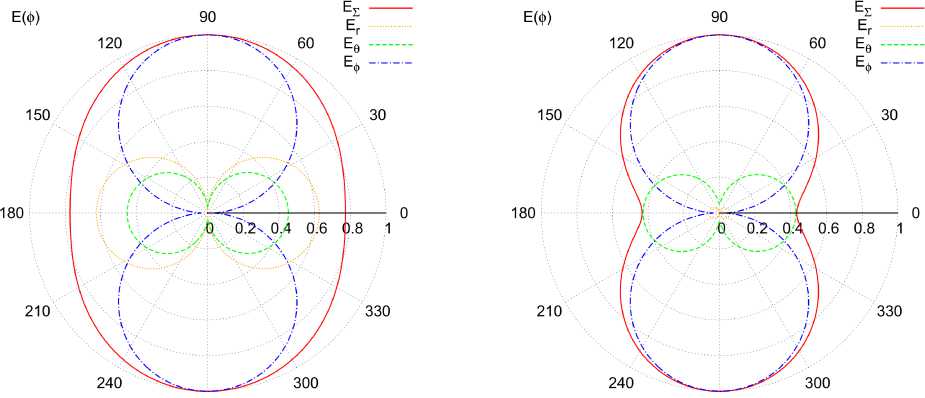
270                                                          270

а                                                   б

Рис. 17. Нормированные диаграммы рассеяния в азимутальной плоскости: а - R / X = 0,005; б - R / X = 0,05. Радиус расчета ρ = 100 R

Fig. 17. Normalized scattering diagrams in the azimuthal plane: a - R / X = 0,005; b - R / X = 0,05. Calculation radius p = 100 R

волны излучения). Параметры МКР, фиксированные при моделировании: rx = ry = rz = r, r / R = 0,3, 8 / rmax =10-3, N = 10, s = 1. На рис. 16 показаны комплексные распределения полного тока вдоль проводника спирали для случаев R / X = 0,005 (а) и R / X = 0,05 (б). Подобные распределения тока трудно отнести к наиболее распространенным режимам стоячих, бегущих или смешанных волн. Можно показать, что у МКР в азимутальной плоскости в рассеянном поле имеется в наличии как компонента Е^, характерная для обычных рамок, так и компонента Eθ (рис. 17). Результаты расчета рассеянного поля, показанные из рис. 17, а, дают основание полагать, что область реактивного поля у МКР простирается значительно дальше, чем у обычных рамок. Эта особенность может создать предпосылки для возникновения интересных эффектов в метаструктурах, построенных на основе МКР.

Таким образом, МКР представляется интересным объектом для дальнейших исследований и может быть использована при создании метаматериалов, широкополосных рамочных антенн и антенных решеток.

4.    Метаматериалы

Аппарат ИП ЭМП также можно с успехом использовать для исследования процессов, протекающих в метаматериалах. Метаматериал - материал, свойства которого обусловлены не столько

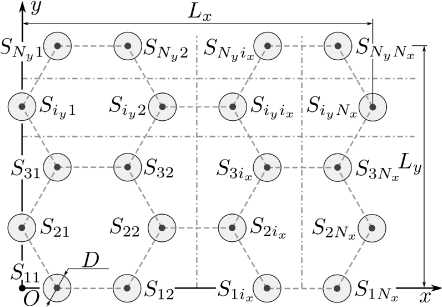
а

Рис. 18. Общая геометрия однослойной метаструктуры ( а ) и геометрия гексагональной ячейки ( б )

Fig. 18. General geometry of a single-layer metastructure ( a ) and geometry of a hexagonal cell ( b )

^Х

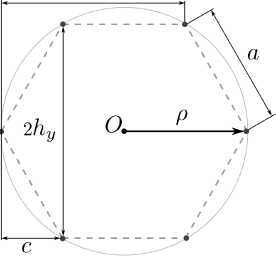
б

природными физическими свойствами, сколько периодической микроструктурой, создаваемой человеком. Основополагающей работой по метаматериалам можно считать работу [16] В.Г. Весе-лаго. В настоящее время метаматериалы находят применение в СВЧ- и антенно-фидерных устройствах, позволяя улучшить их параметры [17]. Примером метаматериалов другого рода являются фотонные кристаллы [18].

В предыдущем разделе было показано, что на основе ИП ЭМП можно получать строгие математические модели базовых элементов метаматериала. При непосредственном анализе метаматериала необходимо также учесть взаимодействия между составляющими его элементами. Проблемы решения внутренней задачи для метаматериала рассмотрены в [19]. Там же показано, что внутренняя электродинамическая задача для метаматериала на основе металлических базовых элементов может быть сведена к блочной СЛАУ вида

Z ^ˆ I = E . (15)

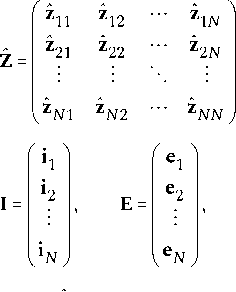
здесь z _{i . j} – проекционные матрицы импедансов, i _j – неизвестные коэффициенты разложения токов на элементах структуры, e _j – коэффициенты разложения стороннего поля на элементах структуры, N – число элементов.

Сделан вывод о нецелесообразности прямого решения данной СЛАУ, и предложено итерационное решение на основе метода Гаусса – Зейделя: i ( ‘ ⁺» = y , e , - ^w j^- ^ j + ') , i = 1 . N ,  (16)

j > г               j < j где i(jk) – k-е приближение для коэффициентов разложения тока yj = z-1, wj = yjzjj. Критерий оценки сходимости строится в соответствии с не- равенством v<5k = max(|j+1) -j)|/|j+1) |), j где a - сколь угодно малое наперед заданное число. Также в [19] представлены алгоритмы вычисления элементов матрицы Zˆ, которые в случае однотипных базовых элементов и регулярной сетки метаматериала могут существенно сократить объем вычислений и машинной памяти.

В качестве примера рассмотрим однослойную метаструктуру с гексагональной сеткой (рис. 18, а ), базовыми элементами которой являются цилиндрические спирали с одинаковой пространственной ориентацией (рис. 19). Возбуждение структуры осуществляется плоской электромагнитной волной (ПЭМВ), распространяющейся против оси Oz и поляризованной вдоль оси Oy . Положение узлов решетки целесообразно определять, используя двойную индексацию. Обозначим индексы вдоль надлежащих осей как i_x , i_y . Радиус описанной окружности гексагональной ячейки обозначим как р (рис. 18, б ) . При осуществлении заполнения матрицы СЛАУ будет применена нумерация составляющих по сквозному индексу i = 1 . N :

^j = ^jx ^{+ ( j}y ^- 1) ^Nx ,                                           ₍₁₇₎

^jX =1... ^Nx , ^jy =1 ^ ^Ny .

Геометрия одиночной гексагональной ячейки представлена на рис. 18, б . Все величины, нужные

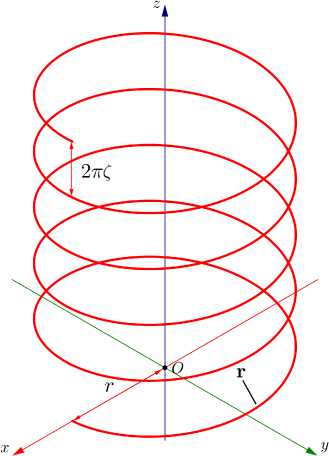
Рис. 19. Базовый элемент метаструктуры

Fig. 19. Basic element of metastructure

нам в дальнейшем, можно получить, зная р . Переменные h x и h y определяют шаг вдоль соответствующей оси прямоугольной системы координат. Для гексагональной ячейки, которая имеет правильную форму, справедливы соответствующие соотношения:

a = р, c = a /2 = р /2, hx = a + c = 3р / 2, hy = Va — c = л/эр / 2.

Определив переменные hx, hy и c, нетрудно получить координаты точек P‘ в глобальной iyix прямоугольной системе координат:

Pi y i x = x 0 ^{( h}x ⁽ i x ^— 1) ⁺ b i_yi_x ^{+ h}x ) ⁺ У 0 ^{( h}y ⁽ i y ^— 1) ^{+ h}y )•

Здесь b i =(1 — mod(i + i ,2))c• iyix                   x y

– дополнительное смещение для точек, а hx , hy определяют смещение решетки вдоль соответственных осей декартовой системы координат. В последующем целесообразно принять hx = — Lx/2, hy = — Ly/2.

Функция mod( x , y ) возвращает остаток от деления x на y . Числа N_x и N y используются для определения числа элементов N x и N y вдоль соответствующих осей:

^Nx = ^{2 N} x , ^Ny = ^{2 N}y — 1,

N x , N y =1,2,... » .

Значения L_x и L_y определяются формулами:

^Lx = ^Nx h x + c , L y = ^Ny h y •

Таблица. Результаты расчета числа существенных элементов

Table. Results of calculating the number of essential elements

p	1	2	3	4	5
N	6	20	42	72	110
а	1,89	4,39	6,46	8,54	8,08
I 1/16	3	4	4	4	4
I 1/4	5	5	5	5	5

Геометрия базовых элементов (цилиндрических спиралей) L показана на рис. 19. Уравнение об-iyix разующей цилиндрической спирали:

r ( l ) = r cos( § l ) x о + r sin( § l ) y о + + Z§ lx z ₀, l e [ — L /2; L /2],

здесь r - радиус цилиндра, Z — коэффициент намотки, § = 1/ V r ² +Z 2 ; L — длина провода спирали. При построении математической модели использовались тонкопроволочное ИП ЭМП (9) и проецирование токов и сторонних полей на элементах структуры с помощью системы тригонометрических функций, обращающихся в нуль на концах интервала:

cos( n п t /2), n — нечетное;

sin( n п t /2), n — четное,                   (19)

T n ( x ) = ^

t e [ — 1;1]; n = 1,2 . T .

Данная система функций близка к собственным (СФ) функциям ИО тонкого прямолинейного проводника [10]. В процессе численного модели- рования выявлено, что она также очень хорошо подходит и для рассматриваемой структуры. Моделирование проводилось для метаструктур с

(j N _x , TV _y ) = ( p , p + 1), p = 1 . 5; р / Z = 1/16,1/4

при следующих фиксированных параметрах: T = 10, R / р = 0,265, e / р = 1/150, N l =2, h / р = = 1/15, 0 0 = 90 ° , § 0 = 90 ° , v = 10 ^{— 6}.

В таблице приведены сведения о параметрах работы численного алгоритма решения внутренней задачи на основе метода Зейделя с оптимизированным вычислением элементов блочной матрицы по строгому алгоритму [19]. Значение p относится к формуле (20), N - общее число элементов структуры, а - отношение числа элементов матрицы Z к числу матричных элементов, необходимых для построения, I р / ^ - число итераций для достижения заданной точности е . Представленная таблица наглядно демонстрирует эффективность предложенного метода.

а

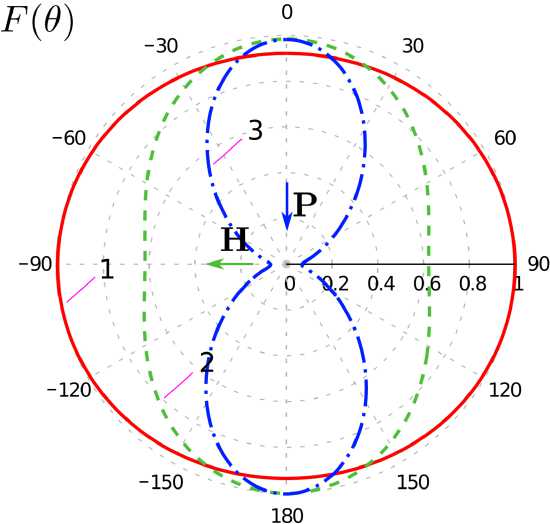
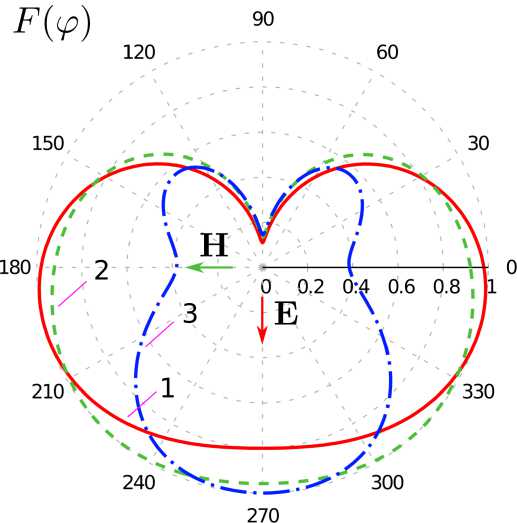
Рис. 20. Нормированные диаграммы рассеяния метаструктур в азимутальной ( а ) и меридианной плоскости ( б ) при различных значениях p в (20): 1 - p = 1, 2 - p = 3, 3 - p = 5; p / X = 1/16

Fig. 20. Normalized scattering diagrams of metastructures in the azimuthal ( a ) and meridian ( b ) planes at different values of p in (20): 1 - p = 1, 2 - p = 3, 3 - p = 5; p / X = 1/16

а

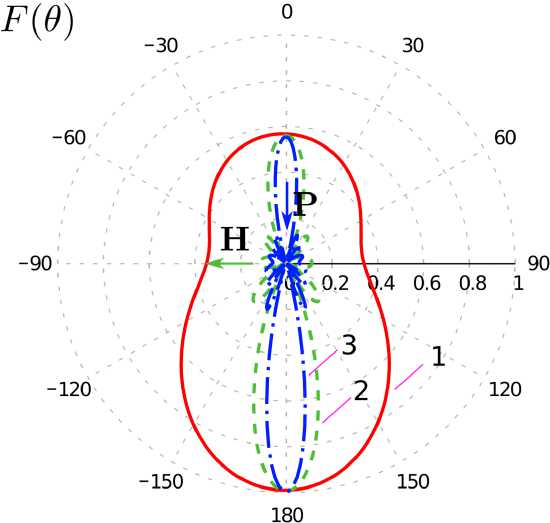
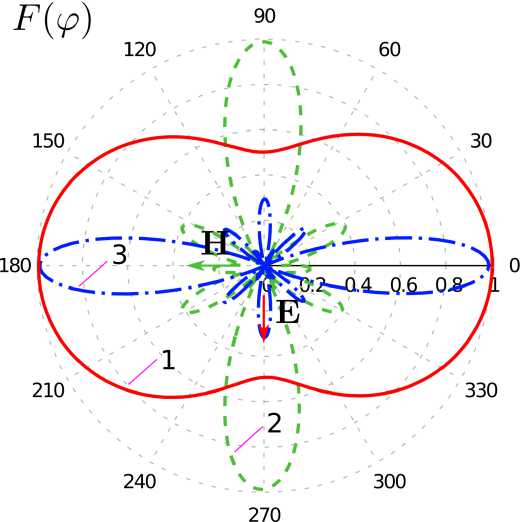
Рис. 21. Нормированные диаграммы рассеяния метаструктур в азимутальной ( а ) и меридианной плоскости ( б ) при различных значениях p в (20): 1 - p = 1, 2 - p = 3, 3 - p = 5; p / X = 1/4

Fig. 22. Normalized scattering diagrams of metastructures in the azimuthal ( a ) and meridian planes ( b ) at different values of p in (20): 1 - p = 1, 2 - p = 3, 3 - p = 5; p / X = 1/4

На рис. 20, 21 приведены рассчитанные с помощью ИП ЭМП диаграммы рассеяния (ДР) структур с различным числом элементов. Видно, что с увеличением числа элементов и ростом частоты происходит сужение лепестков ДР. Также можно отметить асимметрию ДР в азимутальной плоскости при p / X = 1/16, связанную с формой и ориентацией базовых элементов. Асимметрия ДР в меридианной плоскости при ρ / λ =1/4 связана, по всей видимости, с возникновением волноводного эффекта в спиралях.

Заключение

В работе рассмотрены различные формы ИП ЭПМ, в том числе сингулярные. Показано, что использование более развитых в аналитическом плане ИП ЭМП вместо метода векторных потенциалов позволяет существенно облегчить формулировку внутренней и внешней электродинамических задач для конкретных структур. Приведены ИП ЭМП для дальней зоны излучения, обобщенные на случай структур с множеством фазовых центров, а также ИП ЭМП поверхностей враще- ния, тонкопроволочных, трубчатых излучателей и т. д. Рассмотрен механизм выделения особенностей в ядрах ИП ЭМП, необходимый при решении внутренней электродинамической задачи и при расчетах ближнего поля излучающих и переизлу-чающих структур.

Во втором разделе статьи приведены численные результаты некоторых излучающих структур: трубчатого вибратора, двузаходной эллиптической спиральной антенны над бесконечно протяженным экраном и фрактальной антенны на основе салфетки Серпинского. На примере трубчатого вибратора продемонстрирована возможность аппроксимации решения внутренней электродинамической задачи с помощью вычисления собственных функций и собственных значений интегрального оператора СИУ.

Третий раздел посвящен построению строгих математических моделей электродинамических структур на основе ИП ЭМП. Указано, что математические модели большинства базовых элементов, использующихся при создании метаматериалов, можно построить в тонкопроволочном приближении. Предложена математическая модель многозаходной киральной рамки.

В четвертом разделе рассматривается использование ИП ЭМП для анализа метаматериалов. В качестве примера рассмотрена однослойная гексагональная структура, состоящая их одинаково ориентированных цилиндрических спира- лей. Показано, что учет особенностей геометрии и применение проекционных функций, близких к собственным функциям интегрального оператора внутренней задачи для базовых элементов, позволяют строить эффективные алгоритмы электродинамического анализа метаструктур.

Таким образом, метод ИП ЭМП является прекрасным инструментом для построения строгой теории антенн, переизлучающих структур и метаматериалов. Важным моментом является оценка перспектив дальнейшего развития рассмотренного аппарата. Здесь, на наш взгляд, представляются по крайней мере три направления. Во-первых, это более тесное совмещение СИП ЭМП с методом моментов в целях сокращения пути от построения выражений до численного моделирования. Во-вторых, расширение числа ключевых задач, под которыми следует понимать построение СИП ЭМП для множества элементарных излучателей с последующей декомпозицией анализируемой структуры до совокупности элементарных излучателей, наиболее подходящих в конкретном случае. И наконец, третье направление – построение СИП ЭМП, автоматически учитывающих в себе геометрические свойства анализируемых излучающих структур. Подобные СИП ЭМП смогут существенно сократить затраты вычислительных ресурсов и во многом преодолеть недостатки, присущие современным системам автоматизированного проектирования.