Решение задач механики деформирования поликристаллических материалов на основе теории возмущений

Поликристаллические материалы — одни из самых распространенных конструкционных материалов. Ввиду технической важности разработано множество способов описания их механического поведения с различной степенью детализации внутренней структуры. При решении многих инженерных проблем допустимо рассматривать поликристаллы как однородные среды с некоторыми макроскопическими эффективными свойствами, определяемыми экспериментально или на основе тех или иных моделей. Более тонкие эффекты, связанные, например, с локализацией деформаций в статистически однородной поликристаллической среде, носят пороговый характер. К таковым относятся процессы зарождения хрупких трещин или очагов пластического течения. Они начинаются с единичных событий, происходящих в отдельных зернах поликристалла, в которых флуктуирующие напряжения максимальны. Флуктуации связаны с микроструктурой зерен и взаимодействием каждого зерна с окружающими зернами. Интерес к таким явлениям возрос с выделением в материаловедении специального раздела — инженерии зерен,

изучающего методы целенаправленного изменения микроструктуры для достижения заданных свойств конструкционных поликристаллических материалов. Для анализа подобных процессов необходимо знание состояний всех зерен в деформируемом поликристаллическом образце. Ввиду огромного количества зерен и стохастичности их структуры задача очень сложна и требует разработки приближенных методов решения.

В настоящее время наиболее употребимы три метода. Хронологически первым является метод осреднения краевой задачи для неоднородной среды со случайной структурой, сводящийся к вычислению статистических моментов полей деформаций и напряжений. Обычно при вычислениях ограничиваются первым порядком по степени анизотропии зерен и нахождением математических ожиданий и дисперсий случайных полей. Получаемая при этом информация о состояниях отдельных зерен недостаточна. Вычисления с учетом высших поправок пока немногочисленны [1, 2].

Гипотетически наиболее полное описание заключается в решении краевой задачи для поликристаллического тела с точным заданием геометрической структуры всех зерен, а также ориентации их кристаллографических осей в пространстве. Этот подход реализуется в методе прямого компьютерного моделирования [3]. Основная трудность применения метода связана с необходимостью задания значительного объема сведений о точной геометрии большого количества зерен. Современные вычислительные пакеты программ способны оперировать моделями с числом зерен до нескольких сотен или тысяч, что поднимает вопросы статистической достаточности метода.

Третий перспективный метод — метод внутренних переменных. В этом методе вводится ряд феноменологических параметров, отвечающих за эволюцию микроструктуры, ее влияние на деформирование и за другие явления. Параметры входят в постановку задачи и подлежат экспериментальной идентификации. В настоящее время метод интенсивно развивается [4, 5].

В данной работе предлагается подход к разрешению проблемы деформирования поликристаллических материалов, основанный на новом варианте теории возмущений для решения уравнений математической физики. Статья ограничивается исследованием упругих полей в зернах поликристалла при однородном макроскопическом деформировании. Исторически методы теории возмущений возникли в начале 19-го века в небесной механике, где слабое межпланетное гравитационное взаимодействие (по сравнению с взаимодействием планет с Солнцем) рассматривалось как малый параметр — возмущение, в уравнениях движения, а их решение строилось в виде суммы невозмущенного решения и поправок по этому параметру. Наибольшее распространение методы нашли в различных областях физики — от теории нелинейных механических колебаний до квантовой теории твердых тел и квантовой теории поля.

Общая схема метода теории возмущений проста [6]. Применим ее к уравнениям равновесия деформированного тела:

L V = f ,(1)

где L — линейный оператор, ^ — неизвестная функция, f — известная функция. Решение строится следующим образом. Оператор L представляется в виде суммы

L = Lо + L',(2)

такой, что решение «невозмущенного» уравнения L0^<0) = f известно. Тогда решение исходного уравнения можно искать в виде суммы поправок различных порядков у = у<0) + v<1’ + V<2) + V<3) +....<3)

Подстановка (3) и (2) в (1) и итерационная процедура приводят к следующей бесконечной цепочке уравнений, которой удовлетворяют поправки:

L o V <^O) = f , L о ^ <1) =- L V⁰⁾ , L 0 ^ <²⁾ =- L V*) , L 0 _V <³⁾ =- L V²⁾ ,

3        (4)

Сложив все уравнения в (4), убеждаемся, что получается исходное уравнение (1). Метод решения уравнения (4) 1 считается известным. После подстановки ^ <⁰⁾ — решения уравнения <4) 1 , в правую часть уравнения (4 2 ) тем же методом найдем поправку первого порядка ^ <1) , аналогично — v <²⁾ и так далее, то есть полное решение в виде ряда (3).

В [6] отмечается, что формальные схемы методов теории возмущений не имеют в общем случае строгого математического обоснования, в частности в вопросах сходимости. Критерием правильности решения выступает согласование с наблюдаемыми экспериментально явлениями, описываемыми уравнением (1). Примером может служить вычисление величины аномального магнитного момента электрона в квантовой электродинамике [7]. Сумма первых трех членов ряда, представляющего решение, согласуется с экспериментальным значением с беспрецедентной точностью 10–10. В то же время в целом ряд расходится, что было доказано Ф. Дайсоном еще в 1950 году, задолго до того, как такие вычисления стали возможными. Проблема расходимости рядов остается в теории возмущений нерешенной до настоящего времени. Вычисления с использованием теории возмущений часто оказываются очень громоздкими вследствие необходимости оценки интегралов высокой кратности. Для электрона упомянутые вычисления с указанной точностью стали возможными только в 1980-х годах с появлением мощных компьютеров, то есть более чем 30 лет спустя после написания теоретического решения.

Успех применения метода существенно зависит от выбора оператора L ₀ , или, что эквивалентно, решения нулевого порядка ψ ₀ [8]. Решение невозмущенного уравнения может быть известно в точном или приближенном виде. Например, в электронной теории твердого тела в задаче движения электрона в совершенном кристалле за нулевое приближение принимается решение уравнения Шредингера для волновой функции свободного электрона, а взаимодействие электрона с полем кристаллической решетки кристалла считается возмущением [9]. Здесь нулевое решение является точным — это волновая функция электрона в виде плоской волны. Решение в первом приближении, называемое приближением почти свободных электронов, хорошо описывает многие свойства кристаллических твердых тел. В аналогичной задаче движения электронов в кристалле с примесями за нулевое принимается решение для совершенного кристалла, то есть полное решение предыдущей задачи, а влияние полей атомов примеси считается возмущением (метод Корринги–Кона–Ростокера [9]). В этом случае решение нулевого порядка известно лишь приближенно. Если в данной задаче за нулевое приближение взять решение для случая свободных электронов, то получить на деле полезные решения не удается.

В некоторых практически важных задачах возмущение нельзя рассматривать как малое, и часть поправок (не все) имеют один порядок величины с нулевым решением или даже обладают сингулярными особенностями при определенных значениях параметров исходной задачи. Примером служит теория разреженного неидеального бозе-газа в статистической физике [10]. В этом случае суммируют только «главные» члены в разложении решения по поправкам. В [10] отмечается, что в подобных случаях часто общие уравнения и соотношения между физическими величинами трактуются более широко и способны работать также за пределами применимости самой теории возмущений. Несмотря на очевидную математическую нестрогость, такой эвристический подход дает хорошие результаты. Это является еще одной иллюстрацией неразработанности проблемы сходимости теории возмущений.

2.    Традиционный вариант теории возмущений с разложением по неоднородностиупругих свойств поликристаллов

Обратимся к краевой задаче механики неоднородного поликристаллического тела, состоящего из зерен одного типа. Размеры тела предполагаются много большими размеров зерен. Кристаллографические оси индивидуальных зерен хаотически ориентированы в пространстве. Тензор модулей упругости такой поликристаллической среды зависит от координат кусочно-постоянным образом:

N

C ijmn ( r ) = ∑ λ ξ ( r ) C i ⁽ j ^ξ m ⁾ n ( r ),                                                (5)

ξ=1

где λ_ξ ( r ) — индикаторная функция ξ -го кристаллита ( λ_ξ = 1 внутри этого кристаллита и λ_ξ = 0 в прочих кристаллитах); C _i ⁽ _jm ^ξ) _n ( r ) — тензор модулей упругости ξ-го кристаллита (постоянный в его пределах) в глобальной системе координат тела, компоненты тензора связаны с его же компонентами C _i ⁰ _jmn в кристаллографической системе координат кристаллита направляющими косинусами; N — полное число кристаллитов в теле, (макроскопически большое число). По границам зерен обеспечивается идеальный контакт.

Значительные размеры тела позволяют выбрать на его поверхности S граничные условия в перемещениях в виде, соответствующем однородной макродеформации [11, 12]:

ui(r) S =ε*ijxj, где εi*j — тензорная константа.

Один из вариантов метода теории возмущений в этой задаче механики неоднородного поликристаллического тела, состоящего из зерен одного типа, впоследствии ставший традиционным для механики неоднородных материалов, впервые применил И.М. Лифшиц [11] в случае макроскопически изотропного поликристалла. Тензор модулей упругости разлагался на осредненное и флуктуирующее слагаемые

C y« ( r ) = <  C j_H ) + C k ( r ),

и, соответственно, в уравнениях равновесия

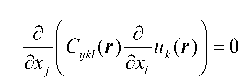
дифференциальный оператор в левой части разбивался на нулевую часть и возмущение:

u_k ^{( r} ) = °.

Таким образом, за возмущение принимается второй член в (6) — неоднородность упругих свойств гетерогенной среды относительно осредненной однородной (в данном случае изотропной). Решение нулевого порядка, определяемое из уравнения

< C и)——

ijkl дXj дxt

«кН ^r ) = °,

находится точно и равняется

^u(4 ^r ) = ^S j x j .

Поправка 1 -го порядка отыскивается из уравнения

< C /ki )^" д X / д X i

u k ^{1,( r} )

d C j_H ( r )

д X /

•^S ki

и имеет вид u^(. r) = JGm (r - Г1) CkiM V                дxij

^kl ^{d r} 1 ,

где V — объем тела, G _im ( r ) — тензорная функция Грина однородной изотропной среды с осредненным модулем упругости ( C _jkl ) , а решение для поля перемещений в первом порядке по возмущению имеет вид:

u i ⁽ r ) » u '”’ ⁺ u^ ⁽ r ) = ^SV j + J G m ^{( r - r} i ) ^д c ”/^{1 ( r i )} •S ki d r . V                ^д x ij

(1°)

Продвинуться дальше в этой схеме трудно. Как правило, решения (9), (1°) используют для нахождения эффективных модулей упругости [11, 12]. Получающиеся выражения для эффективных модулей Юнга и сдвига не зависят от формы и размеров кристаллитов, то есть микроструктуры поликристаллического материала [11]. Некоторая информация о влиянии микроструктуры получается в результате определения статистических моментов случайного поля ui (r) на основе решения (1°). Однако и на этом пути для поликристаллов с анизотропными зернами можно вычислить лишь несколько параметров, обычно, средних значений и дисперсий искомых величин. Работ, в которых бы учитывались поправки более высоких порядков по возмущению, практически нет. В работе [1] устанавливались эффективные модули поликристаллов с кубической анизотропией зерен и при учете поправок высших порядков, но с дополнительными упрощающими предположениями.

В поликристаллических материалах многие явления носят локальный или пороговый характер. Например, в упруго-хрупких поликристаллах при увеличении нагрузки первые акты хрупкого разрушения (или повреждения) имеют место сначала в одном или нескольких кристаллитах, в тех, у которых флуктуирующие локальные напряжения максимальны. Аналогичным образом начинается пластическое течение в поликристаллах. Для описания происходящих процессов необходимо знание индивидуальных состояний всех кристаллитов или функций распределения полей деформаций и напряжений в кристаллитах, по которым можно вычислить вероятности соответствующих событий. Традиционная теория возмущений, изложенная выше, не дает такой возможности.

В настоящей работе предложен новый вариант теории возмущений для краевой задачи механики поликристаллов, позволяющий получить решение для поправок всех порядков, учесть влияние микроструктуры материала на деформированное состояние индивидуальных зерен, вычислить функции распределения полей деформаций и напряжений и другие важные параметры деформирования поликристаллических материалов. Суть метода состоит в новом выборе нулевого решения исходной задачи.

3.    Формальная схема теории возмущений по межзеренному упругому взаимодействию

Для реализации новой схемы решения методом теории возмущений удобно перейти от дифференциальных уравнений к эквивалентным интегральным уравнениям, как это принято в статистической физике и квантовой теории поля [10]. Точные уравнения равновесия для неоднородной среды (7) в интегральной форме записываются для тензора деформаций как [12, 13]

^е j ⁽ r ) = ^s j + j" g ijki ( r ^- r 1 ) C kmn ( r 1 ) ^s _mn ( r ) d r 1 , V

где g jki = j G ik л + G jk,« )

— тензор Грина среды с изотропным тензором модулей упругости

( C ijki > ,

а G ik , jl — вторая производная тензора Кельвина-Сомильяны. Тензор Грина имеет вид:

12 . _ gijki(r) = - ,     (1 -X)VijH +(1 - у X)Di j           3(ц>L j 5 i

^{5 (} r ) + n , ¹ I |3 L ³ ( nn ⁵ jk + n j n ⁵ ik ) - ² j +

8 п(ц> | r| ^L

+x ( I jki + I j + Ink )^{- 3} x ( ^{nn 5} ki + n i n k ⁵ jl + nn ⁵ jk + n j n k ⁵ ii + n^ ⁵  + n k n i ⁵ ij - ⁵ n i n / n k n i ) ] ,        ⁽¹²⁾

3(K> + (ц>                     „              J                              ,     1            _ \

x _i

r

где x= --материальный параметр, o„ — символ Кронекера, I -_; =— I 5_k5._;+5_;5._k ) , n =

3(K> + 4(ц>                                           ij                                  j 2х ik jl     “ Jk) i направляющие косинусы радиус-вектора r в глобальной системе координат. Для нетекстурированных поликристаллов осредненный тензор изотропен: (Cijkl> = 3(K>Vjkl + 2(ц>Dijk, где (K> и (ц> — средние модули объемного сжатия и сдвига, а Vjkl и Dijkl — шаровая и девиаторная части единичного тензора Iijkl. Формулы для вычисления средних модулей упругости поликристаллов всех сингоний приведены в [12].

Представим глобальный тензор деформаций s j в виде сумм деформаций в кристаллитах е j ⁾ с помощью индикаторных функций Х , :

N

^s j ⁽ r ) = Х\ ^{( r ) е} j³ r ).

,=1

Подстановка разложения (13) и тензора модулей упругости (5) в (11) позволяет разбить интегральное уравнение для глобальных деформаций (11) на N уравнений для деформаций в зернах:

е ^(у ( r ) = е * + [ d r ' g _и( r - r Л Г[ C L^y ( Я ' ) -( C,, ))ls ⁽⁵⁾ ( r /) + ij x ^ / tj J ^ o ijk;lv ^      ^ I \ klmnv ^7    \ klmn/ ) I mnv ^7

^

+ Z f d r ' g jk. ( r ' - r ' ) L ( C« m ’ ( r ' ) -( C klmn > ) ]s mn ^>( r _n' ),

П#^шл где r, — радиус-вектор в пределах ^-го кристаллита, а ю^ — объем этого кристаллита. Выражения (14) есть система 6N интегральных уравнений для 6N неизвестных функций е®(r,). Она означает, что деформация в какой-либо точке выбранного с-го зерна является результатом суперпозиции внешней макродеформации е*, деформаций в других точках этого же зерна и деформаций во всех остальных зернах поликристаллического тела. Два последних континуальных набора деформаций входят в суперпозицию с весовыми коэффициентами, выраженными подынтегральными ядрами во втором и третьем членах правой части (14). Эти ядра определяют, соответственно, внутри- и межзеренное взаимодействие деформаций. Видно, что взаимовлияние зерен убывает по мере удаления их друг от друга, так как подынтегральная функция затухает по закону gijkl ~ 1/r3.

Примем за возмущение сумму в правой части (14), которая отвечает за межзеренное взаимодействие, отнеся к нулевому решению внутризеренное взаимодействие деформаций, описываемое вторым слагаемым правой части (14), и применим к уравнениям (14) схему (1)-(3). Получим следующую совокупность N бесконечных цепочек систем уравнений:

_е(^(гЛ- Г g-г^С® 8⁽°^)(,)(№ е*, j       ,'    J gijkl V ,     ,/ тПтптщп   V , / ^ ,     '-'у ,

i

ГО е j1)(,) (r,) - J gtiti (r, - r‘)Cn етn® (r^dr’=/ J gjki (r - оckm ет°г (о dr;, to,                                               П^ ton

е(2)(,)(r)- |"g (rr -r,)CL(y е(2)(,)(r,)dr/ = У fg H(r -r')C'(n) е(1)(;)(r')dr ij V , / I gijkl V ,      ,' klmn mn V , /   ,     / * I gijkl \ ,      ;/ klmn mn V ;' П, to,                                                          n*^ ton е (ji,R,( r,)-J gijkl(r,- rD Cumn е^ч rp щ=Х1 sw(r,- r;) Cm е<тп)<;)( r;) dr; итак далее, го,                                                          n*, to;

где , , ; = 1, 2,..., N , а для отклонений локальных модулей упругости от среднего введено обозначение:

C ⁾ = C ( r ) -< C jki > .                                                (16)

Полное решение исходных уравнений (14) равно сумме всех поправок:

е (^ r , ) = е (“^)(,) ( r , ) + е      r , ) + е j²’^ r , ) + е       r , ) + ....                             (17)

После подстановки решений для деформаций в зернах (17) в (13) получим решение краевой задачи для глобальных деформаций во всей поликристаллической среде. В левых частях уравнений (15) стоит один и тот же интегральный оператор. Найдя способ решения уравнения (15) 1 , последовательной подстановкой отыщем поправки всех порядков. Из (15) 1 видно, что даже в нулевом приближении по межзеренному взаимодействию деформация в кристаллите зависит от его формы и размеров. Решить (15) точно в общем виде вряд ли возможно. Основная трудность проистекает от координатной зависимости неизвестных функций е j °⁾⁽^⁾( r , ), е ij ^1)(,) ( r , ), е j²’^ r , ),....

В литых и спеченных поликристаллических материалах зерна в среднем имеют форму выпуклых многогранников, близких к сферам. Это минимизирует поверхностную энергию границ зерен во время кристаллизации поликристаллов из расплава или спекания из порошков. В сферическом зерне, погруженном в осредненную среду остальных зерен, поле деформаций, как показано Эшелби, однородно [14]. Это позволяет предположить, что неоднородность поля деформаций в зернах поликристаллического материала мала.

Рассмотрим случай, когда неоднородностями можно пренебречь. Полагая функции е j ^0)K)( r ,), е®⁽^’( r ,), е j ^2,<У( r ,), ... постоянными в пределах зерна, возьмем их значения в центре этого зерна и обозначим как е j ^0)ra, е j ¹’®, е(^2Ж), .... Тогда системы интегральных уравнений сведутся к системам линейных алгебраических уравнений:

-R (,,)Ъ(°)(,) - р*

L ijM    ijkykl )^е kl         ^еij ,

Г Т _ D (,,)"| р(1)(,) _ V R(,n)p(°)(n)

L I ijkl     B ijkl J⁶ kl          / , B ijkl ^е kl     ,

;*,

Г T _ D (,,) "I _c(2)(,) _ V R(,n)p(1)(n)

L I ijkl    B ijkl J⁶ kl     = / B ijkl ^е kl 1

;*,

Г T      R (,,)"lp(3)(,) _ V R(,n)p(2)(n)   _т,

L I ijkl ^- B ijkl J⁶ kl = / B ijkl ^е kl      и ^так далее,

;*, где

В. ^Kn) = I" dr's _и(г. ijmn J n g ijklV , to_n

—

' (n)

klmn

—

( C klmn ) )

есть постоянные коэффициенты. Каждое из уравнений в (18) в действительности представляет собой подсистему из шести линейных алгебраических уравнений для шести компонент тензорных поправок деформаций в каждом порядке £ j ^0)(y, £ j ¹'"', £ ⁽ j ^2№),.... Они могут быть решены современными численными методами.

Уравнения (18) применимы для решения нескольких типов задач. Во-первых, для конкретной реализации микроструктуры поликристаллического образца, которая задается совокупностью коэффициентов (19), можно найти деформации во всех зернах, то есть полностью описать деформированное состояние поликристаллического тела заданной структуры. То же самое получается как при прямом компьютерном моделировании геометрической структуры поликристалла, так и численном решении краевой задачи для модельного тела, но, в отличие от компьютерного моделирования, краевая задача разрешима для поликристалла с очень большим числом зерен. Подобные задачи относятся к детерминированным.

В случае макроскопических поликристаллических тел, содержащих очень большое количество зерен (порядка 106 и выше) более рационален статистический подход. Можно анализировать зависимость конкретного состояния одного выделенного зерна (то есть зерна определенной формы и ориентации) от случайной структуры окружающих зерен. Такой тип задач относится к локально статистическим при условии, что случайным является только окружение зерна. Он представляет интерес для анализа поведения одиночных включений, частиц упрочняющей фазы или других изолированных неоднородностей в поликристаллической среде. Для однофазных же поликристаллов становится осуществимой оценка степени влияния окружающей микроструктуры и упругого взаимодействия на состояние индивидуального зерна.

Для статистического описания макроскопического поликристаллического тела в целом адекватен подход, который можно назвать глобально статистическим. В этом случае деформации в зернах £ ®( г , ) следует рассматривать как случайные функции на ансамбле всех возможных конфигураций поликристалла. Очевидно, что этот тип задач состоит из совокупности задач предыдущего «локального» типа, в каждой из которых случайным образом выделяется одно зерно.

Кроме того, изложенный формализм дает возможность решать некоторые задачи общетеоретического характера. В предлагаемой вниманию работе остановимся лишь на одной из таких задач — количественно исследуем характер и особенности упругого взаимодействия зерен в различных поликристаллах. Для этого запишем решение систем (18) в формальном виде:

Р(0)(§> _ Л^р*

^£ ij          A ijkl ^£ kl ,

Р0Ж) _ V /f(,n)p(0)(n) £ij        / . Aijkl £ kl    , n#s

P(№ _ V д(,п)р(0)(л) £ij       / Aijkl £ kl    , ч-,

£ j ^3)ra = / A jk? ⁾ £ ⁽ _k ²⁾⁽ⁿ⁾ и так далее,

Ч-, где для коэффициентов введены обозначения:

л (Я₌Гг Д            л(Е.п) ₌ Г г _ оЖЯ ¹ oRn) _ Ж9 тЖп)                   /-in

Aijkl ^— V. ijkl У^и J ’          ijkl ^— L У™ ijmn J m™nM     ijmn mnkl ^{.                          (} )

Сложив все уравнения (20), получим уравнение, связывающее полные деформации во всех зернах поликристалла:

Р (У _ А* , V л<5п)р(п) ^£ ij      A ijkl ^£ kl + / A ijkl ^£ kl .

ч-,

В таком виде систему уравнений (22) решить нельзя, так как она содержит макроскопически большое количество уравнений и неизвестных, но можно сделать важные выводы о характере межзеренного взаимодействия. Первый член в правой части есть решение краевой задачи для деформаций при полном пренебрежении межзеренным взаимодействием, однако, с учетом внутризеренного взаимодействия деформаций. Даже такое простейшее приближение дает много информации о состоянии зерен [15, 16]. Члены под знаком суммы — это результат межзеренного взаимодействия. Тензорные коэффициенты A jn ⁾

безразмерны. Из (22) видно, что для каждой пары зерен (tn) коэффициенты Am) определяют интенсивность взаимодействия компоненты деформации s® в t-м зерне с компонентой деформации бк1п) в η-м зерне. Они зависят от упругих модулей зерен, формы и размеров зерен, от взаимной ориентации кристаллографических осей и расстояния между зернами. Иными словами эти коэффициенты зависят от микроструктуры поликристалла. Тензор Am) симметричен по перестановке индексов первой и второй пары, но, вообще говоря, несимметричен по перестановке пар индексов. Таким образом, взаимодействие шести компонент тензора деформации в одном зерне с шестью компонентами тензора деформаций в другом зерне описывается 36 коэффициентами Am). Сложившаяся ситуация качественно отличается от ситуации в классической механике, где взаимодействие дискретных частиц изображается всего одной функцией — скалярным потенциалом взаимодействия. Тензор Am) можно назвать тензором взаимодействия зерен в поликристалле.

Структура уравнений (22) показывает, что вклады в состояние ξ-го зерна от взаимодействия с другими зернами линейно суммируются с весовыми коэффициентами A m) . Это позволяет говорить о парном характере взаимодействия зерен и исследовать интенсивность упругого взаимодействия отдельных пар зерен в зависимости от расстояния между зернами, их формы, взаимного положения зерен и взаимной ориентации их кристаллографических осей. В настоящей работе количественно анализируются особенности упругого взаимодействия на примере поликристаллов с зернами различных упругих сингоний.

4.    Особенности упругого взаимодействия зерен различных типов

Сначала исследуем характер зависимости межзеренного взаимодействия от типа упругой симметрии зерен. Для этого зафиксируем два каких-либо зерна, то есть оставим неизменными их форму и взаимное расположение, но будем варьировать тип упругой симметрии зерен, включая взаимную ориентацию кристаллографических осей и числовые значения модулей упругости. Из развернутого выражения для коэффициентов тензора взаимодействия

- -1

A^(tn) = i mn

I ijkl - J d r t g ijkl ⁽ Ч- rD ■ ( ^C kZ -< C klpr ) ) J d r ’ g prst ⁽ r - r n ) ■ ( C^ ^- ( C stmn ) )

Ю                                 j  ю, видно, что требуется вычислять интегралы по областям обоих зерен, и t, и п, то есть задавать конкретную микроструктуру поликристалла. Вычисления проведем на двух модельных поликристаллах с зернами одинакового объема, но разной формы — кубической и сферической, показанных на рисунке.

Структуры модельных поликристаллов

Несмотря на то, что сферические зерна нельзя геометрически упаковать в сплошную среду, такая модель часто используется в механике композитов [17]. В излагаемом подходе сферичность зерен присутствует только при вычислении интегралов, где реальные области интегрирования ю , , имеющие вид многогранников, заменяются шаровыми областями, что вносит некоторую погрешность в результат вычисления интегралов, но не связано с проблемой упаковки. У кубических зерен такая проблема отсутствует.

Рассмотрим три характерные упругие сингонии — орторомбическую (уран), гексагональную плотную упаковку (цинк) и гранецентрированную кубическую (алюминий). В качестве взаимодействующих зерен возьмем два ближайших зерна, расположенных вдоль оси координат x1 , с кристаллографическими осями, параллельными друг другу. Оси упругой симметрии совместим с осями координат. В случае гексагональных зерен ось упругой симметрии 6-го порядка зерен направим вдоль оси x3 системы координат. Необходимые для вычислений значения компонент тензоров модулей упругости С0тп кристаллов урана, цинка, алюминия возьмем из монографии [18].

Результаты вычислений для упомянутых материалов с модельными зернами кубической формы приведены в таблице 1.

Таблица 1. Коэффициенты взаимодействия для урана, цинка, алюминия

Индексы	А к -103
	11	22	33	23 и 32	13 и 31	12 и 21
11	28,6/50,5/-16,7	2,76/-32,9/8,29	-57,5/32,8/8,43	-0,54/0,001/0,002	-0,007/0,016/0,006	-0,004/0,17/-0,002
22	-23,9/1,19/5,13	177/-8,07/1,18	4,12/-28,1/-6,32	4,30/0,14/0,0044	-0,006/0,023/0,006	-0,005/0,067/0,024
33	3,04/-22,7/4,51	-65,4/13,2/-5,81	-1,83/33,1/1,31	-7,34/-0,56/-0,11	-0,003/-0,11/-0,082	-0,0004/-0,31/-0,021
23 и 32	-3,64/7,08/-0,30	14,5/-4,31/0,35	2,44/-9,15/-0,052	-19,7/5,48/-1,99	-0,002/-0,052/-0,036	~ 0/0,011/-0,005
13 и 31	-5,67/7,18/-0,47	20,0/-4,36/0,41	4,17/-8,87/0,061	-5,65/-0,21/-0,065	0,17/1,27/-1,12	-0,007/-0,036/-0,014
12 и 21	-2,22/1,82/-0,14	7,44/-1,11/0,16	1,66/-2,26/-0,021	-2,36/-0,021/-0,012	-0,012/-0,0005/-0,013	0,12/-2,48/-1,10

Для урана значения всех коэффициентов заключены в пределах J a™! <  0,177, для цинка — |А( ™’| <  0,0505 , для алюминия — | A ,j ^1 < 0,0167. Величины коэффициентов зависят не только от типа анизотропии, но и от конкретных значений упругих постоянных монокристаллического зерна. Однако в большинстве случаев для всех кристаллов коэффициенты растут с понижением класса упругой симметрии. Для формально изотропных зерен коэффициенты взаимодействия тождественно обращаются в нуль. Если изменять взаимное положение зерен (оставляя неизменным расстояние между их центрами) и взаимную ориентацию кристаллографических осей, то значения всех коэффициентов меняются, но остаются примерно в тех же пределах. Аналогичные вычисления для модельных поликристаллов со сферическими зернами показывают, что соответствующие значения коэффициентов взаимодействия изменяются не более чем на 10%. Это означает, что интенсивность упругого взаимодействия в большей степени зависит от типа упругой сингонии зерен, чем от их формы.

Некоторые (особенно тугоплавкие) монокристаллы кубических сингоний являются практически изотропными: для них отклонение параметра анизотропии a = ( C ₁ ⁰ ₁₁₁ - С ”₂₂ ) JiC 0₃₂₃ от единицы (таково его значение для всех изотропных материалов) ничтожно мало. Примерами служат вольфрам, рений. Для вольфрама с модулями упругости монокристаллического зерна из справочника [18] имеем: Сш = 502,0 ГПа; C 0₂₂ = 199,0 ГПа; C ₂ ⁰ ₃₂₃ = 151,5 ГПа; все коэффициенты взаимодействия А , ^П) в точности обращаются в нуль. Состояние всех зерен в таких поликристаллах определяется уравнением (20) 1 , то есть зависит только от свойств данного зерна (его формы и ориентации осей) и граничных условий для всего поликристаллического тела (через макродеформацию s ^ ) . Это еще раз иллюстрирует решающее влияние типа упругой симметрии зерен на интенсивность их взаимодействия.

5.    Зависимость интенсивности упругого взаимодействия зерен от расстояния

Выделим какое-либо индивидуальное зерно и исследуем, как далеко простирается влияние упругого взаимодействия с другими зернами на значение деформации s® в этом зерне. Поправка нулевого порядка s j <№) = " j - ba p ] s*_fci обуславливается только свойствами этого зерна и его геометрией. Все эффекты межзеренного взаимодействия заключены в поправках 1-го и высших порядков (20). Разобьем каждую сумму в правых частях уравнений (20) на подсуммы по зернам, являющимся ближайшими соседями, далее по зернам, следующим по удалению за ближайшими соседями и так далее (по аналогии с теорией жидкостей и аморфных тел эти группы зерен будем называть зернами 1-й, 2-й и так далее координационных сфер); на фрагментах рисунка цветом выделены зерна 1-й и 2-й координационных сфер.

С учетом сказанного система (20) примет вид:

(0)(ξ)        (ξξ) *

• ε ij = ijkl ε kl ,

1st                     2nd3

(1)(ξ)             (ξη) (0)(η)             (ξη) (0)(η)             (ξη) (0)(η)

ε ij = ∑ A ijkl ε kl + ∑ A ijkl ε kl    + ∑ A ijkl ε kl + ...,

η≠ξ                η≠ξη≠ξ

1st                     2nd3

(2)(ξ)             (ξη) (1)(η)             (ξη) (1)(η)             (ξη) (1)(η)

ε ij    = ∑ A ijkl ε kl + ∑ A ijkl ε kl   + ∑ A ijkl ε kl + ...,

η≠ξ               η≠ξη≠ξ

1st                     2nd3

ε (3)(ξ) =     A (ξη) ε (2)(η) +     A (ξη) ε (2)(η) +     A (ξη) ε (2)(η) + ... и так далее.

ij                            ij                                       ijij

η≠ξ                η≠ξ                η≠ξ

Снижение интенсивности упругого взаимодействия двух зерен с увеличением расстояния между ними определяется скоростью уменьшения значений компонент тензора взаимодействия A _i ⁽ _j ^ξ _m ^η _n ⁾ . Из развернутого выражения (23) для этих коэффициентов видно, что величина A _i ⁽ _jm ^ξη _n ⁾ зависит не только от расстояния между областями интегрирования ω_ξ и ω_η , но и от их положения по отношению друг к другу, то есть от угловых координат, а также ориентации кристаллографических осей обоих зерен, задаваемых тензорами (ξ)           (η)

ijkl и ijkl .

В качестве приложения изложенного формализма проведены вычислительные эксперименты на двух модельных поликристаллах цинка с кубической и сферической формами зерен одинакового объема. Результаты показали, что все коэффициенты взаимодействия изменяются синхронно расстоянию, хотя могут иметь разный порядок величины. Для примера в таблице 2 приводятся числовые значения двух компонент тензора взаимодействия, описывающих взаимодействие нормальных деформаций друг с другом и сдвиговых друг с другом в зависимости от расстояния, выраженного в единицах диаметра зерна, для зерен кубической формы.

Таблица 2. Зависимость коэффициентов взаимодействия от расстояния между зернами, выраженного в единицах диаметра зерна

Расстояние Коэффициент	1	2	3	4	5	6	7
A 1111 ·103	50,500	10,270	3,243	1,391	0,719	0,418	0,264
A 1212 ·103	–2,480	–2,076	–0,721	–0,318	–0,166	–0,097	–0,062

Данные таблицы 2, в силу вышеизложенного, иллюстрируют общий закон уменьшения интенсивности упругого взаимодействия зерен с ростом расстояния между ними. Видно, что отношение интенсивности взаимодействия с зернами далеких координационных сфер к интенсивности взаимодействия с зернами 1-й координационной сферы (ближайшего окружения) убывает достаточно медленно. Лишь для 5-й координационной сферы это отношение достигает 1,4% для нормальных деформаций и 6,79% для сдвиговых. Для 6-й координационной сферы эти отношения составляют 0,83% и 3,9%, соответственно, для нормальных и сдвиговых деформаций. Таким образом, упругое взаимодействие зерен распространяется на довольно значительное расстояние. С точностью до 5–6% надо учитывать взаимодействие с зернами первых пяти–шести координационных сфер.

Полученные результаты можно использовать для оценки размеров представительного элемента объема поликристаллического материала. Очевидно, что размер представительного элемента должен быть, во всяком случае, больше области, в которой взаимодействие центральных зерен с периферийными еще существенно. Первые пять координационных сфер (кубов для кубических зерен) содержат 11×11×11=1331 зерно. Это может служить ограничением снизу размеров представительного элемента объема поликристаллического тела. Величина представительного объема существенна для методов осреднения в механике поликристаллов и при прямом компьютерном моделировании. Также она позволяет установить размеры поликристаллического тела, при которых его допустимо рассматривать как однородное с эффективными модулями. По определению линейный размер тела должен быть намного больше линейного размера представительного объема. Если принять кратность этого превышения размеров равным 10, то линейный размер тела составит 110 диаметров зерна, а количество зерен в теле — 110×110×110=1331000. Таким образом, поликристаллическое тело допустимо считать однородным с эффективными свойствами при числе зерен больше миллиона. Это важно при оценке точности метода прямого компьютерного моделирования, для которого в настоящее время доступны модели с количеством зерен не больше нескольких тысяч. Вычислительные эксперименты на поликристаллах цинка со сферической формой зерен показали, что отличие численных результатов от приведенных выше в таблице 2 не превышает 6–7%.

Анализ результатов расчетов на сферических зернах позволил выявить интересную особенность их упругого взаимодействия. Если рассмотреть сферическое зерно, окруженное концентрическим шаровым слоем однородного материала, то оказывается, что все коэффициенты взаимодействия обращаются в нуль. То есть сферическое зерно не взаимодействует (в смысле влияния на его состояние) со сферическим однородным окружением. В частности, если выделить сферическое включение в неограниченно большой матрице (с произвольными анизотропиями включения и матрицы), подверженное на бесконечности деформации s’-, то деформация внутри включения будет равна

-1

s

(« =

I.... - f dr(rf - о ■ fс® - mmatrix)) ijk!          ^ gtjkl ^      ^ klpr    kiklpr го^

*

^s pr .

Для изотропного сферического включения в изотропной матрице интегрирование и обращение тензоров в (25) можно произвести аналитически. Результат совпадает с решением Эшелби 1957 года для деформации внутри включения [14].

6.    Заключение

В работе предложен новый метод решения краевой задачи теории упругости для неоднородных тел поликристаллической структуры с произвольной анизотропией зерен. Метод основан на новом варианте теории возмущений, в котором за возмущение принимается интенсивность межзеренного упругого взаимодействия. Все эффекты внутризеренного взаимодействия деформаций учитываются в нулевом решении. Такое разделение взаимодействий позволяет анализировать влияние типа анизотропии зерен на интенсивность упругого взаимодействия зерен, характер спада интенсивности взаимодействия в зависимости от расстояния, а также сделать другие важные выводы.

В приведенных примерах метод реализован в приложении к однофазным поликристаллам, но в равной степени он применим и к многофазным поликристаллическим материалам

Работа выполнена при финансовой поддержке РФФИ (проекты № 16-01-00682-а, 15-01-06912-а и 16-01-00327-а).