Решение задач нечткой логики в среде MATHCAD

Нечёткая логика является обобщением традиционной Аристотелевой логики для случая, когда истинность рассматривается как лингвистическая переменная, которая может принимать значения такого типа, как «очень истинно», «более-менее истинно», «не очень ложно» и т.п. [1]. Такие лингвистические значения интерпретируются в виде нечётких множеств [2].

Проблема, выдвинутая автором статьи, связана с выбором средств для решения задач практического характера. Для решения названных задач достаточно широко и успешно используются такие среды, как MATLAB и fuzzyTECH, позволяющие строить нечёткие модели систем в технике и экономике [3]. Но в рамках небольших спецкурсов по математике их использование становится нецелесообразным, т.к. требуется дополнительное время для изучения и освоения самих этих средств.

В качестве решения указанной проблемы автор статьи предлагает такие методы решения задач нечёткой логики, которые позволяют использовать распространённый и популярный программный продукт MATHCAD [4].

В первой части статьи описаны способы решения задач нечёткой логики с использованием двухколонных матриц для определения нечётких множеств. Вторая часть статьи посвящена построению нечётких баз знаний с использованием функций двух переменных.

Операции нечёткой логики

В теории нечёткой логики особое место занимает лингвистическая переменная «истинность». В традиционной логике переменная этого типа может принимать только одно из двух значений: «истина» или «ложь». В нечёткой логике истинность определяют аксиоматически, причём различные авторы делают это по-разному. Для определения лингвистической переменной «истинность» в качестве универсального множества используется интервал [0, 1]. Например, Балдвин [5] предлагает для определения значений переменных «истина» и «ложь» использовать следующие функции принадлежности:

^Ц „истина”’ (u) ^u, ^Ц_1Г ложь”’ (u) = 1-u, где u e [0,1] (1)

Для нечётких логических переменных «истина» и «ложь» очень часто применяют квантификаторы «более-менее» и «очень», получая таким образом новые термы: «более-менее истинно», «очень ложно», «более-менее ложно» и др. Чтобы определить функции принадлежности новых термов, по отношению к нечётким множествам «истина» и «ложь» выполняют операции концентрации и растяжения.

Операция концентрации соответствует возведению значений функции принадлежности в квадрат, а операция растяжения - извлечению квадратного корня.

Например, функции принадлежности для термов «очень ложно», «более-менее ложно», «более-менее истинно» и «очень-очень истинно» можно определить следующим образом:

^Ц ”очень ложно”⁽ и) = ⁽ Ц ”ложно”⁽ и ⁾⁾

^Ц ”более-менее ложно”⁽ и) = ^{( ц} ”ложно”^(и))

^Ц ”более-менее истинно”^(и) = ^{( ц} ”истинно”^(и))

^Ц ”очень-очень истинно”^(и) = ^{( ц} ”очень истинно”^(и)) = ^{( ц} ”истинно”^(и))

Функции принадлежности термов, определённые по формулам (2), изображены на рисунке 1.

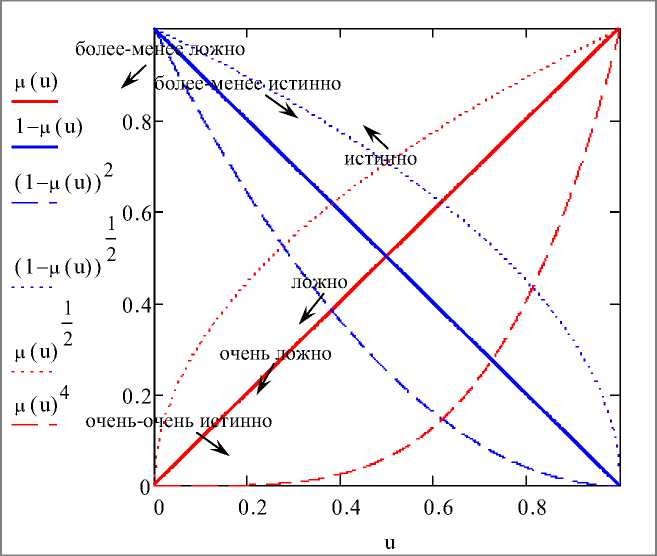
Рис. 1. Лингвистическая переменная «истинность» по определению Балдвина

Обозначим через Ã и B^~ две нечёткие логические переменные, а их функции (или степени) принадлежности - ц ~ (u) и ц ~ (u) соответственно, где u e [0,1]. Операции нечёткой конъюнкции (AND - л ), дизъюнкции (OR - v ), отрицания (NOT - А) и импликации ( ^ ) выполняются по следующим правилам:

ц А лВ (u) = min (ц А (u), ц В(u))

ц А vB(u) = max (ц А (u ) ц В(u))

ц ~(u ) = 1 - ц А( u )

ц А ^В(u) = max (1 - ц А (u), ц В(u))

Если эти функции заданы аналитически, выполнение соответствующих операций не вызывает проблем, т.к. точно таким же образом их можно определять в среде MATHCAD. Но, если переменные нечёткой логики заданы в виде дискретных нечётких множеств с указанием степеней принадлежности отдельных значений, в среде MATHCAD их можно интерпретировать в виде матриц, состоящих из двух столбцов, первый из которых содержит возможные значения переменной, а второй – значения их степеней принадлежности. Сами логические операции можно определять с помощью небольших программных модулей.

Пример 1 .

Даны две переменные нечёткой логики:

~   0  0.2  0.35  0.45  0.850.9

А = - + — +--+--++ —

0  0.2   0.4   0.6    0.81

Найти

B~

0.1  0.15  0.25  0.6  0.9  1

— +--+--+ — + — + _

0    0.2    0.4   0.6  0.8  1

A v B ) л ( Л v B ) .

Примечание : здесь и далее для упрощения ввода данных в среде MATHCAD символ тильда ( ~ ) в обозначениях нечётких переменных будет опущен.

Матрицы, определяющие значения A un B, показаны на рисунке 2.

ORIGIN := 1

	< 0	0		f 0	0.1 >
	0.2	0.2		0.2	0.15
	0.4	0.35		0.4	0.25
A:=	0.6	0.45	В :=	0.6	0.6
	0.8	0.85		0.8	0.9
	< 1	0.9 ,		v 1	1 >

Рис. 2. Матрицы, определяющие нечёткие логические переменные A и B

Далее, используя формулы (1) и (3), можно определить значения Л v B (рис.3) и Л v B (рис. 4). Затем следует вычисление значений конечного результата (рис. 5), которые, в случае необходимости, можно интерполировать (рис. 6).

notB :=

for iel.. 6

notB; । «- В, ]

notB; 2 <- 1 - В,2

notB

notB =

A or notB :=

for ie 1.. 6

О

0.2

0.4

0.6

0.8

0.9 А

0.85

0.75

0.4

0.1

0 J

AoinofBi i <- А; 1

AornotB, 2 *- maxi Aj 2, notB, 21

A oi' notB

A or notB =

' 0	0.9
0.2	0.85
0.4	0.75
0.6	0.45
0.8	0.85
< 1	0.9 ,

~~

Рис. 3. Определение значения Л v B

not А :=	foi	ie 1.. 6 not A] 1 <— A, i , . < v i v .       notA = notA, 2 ^ 1 * jXj 2			0    1 0.2 0.8 0.4 0.65 0.6 0.55
	nofA				0.8 0.15
notA_or_	В :=		foi	ie 1.. 6	, 1 0.1 ,		' 0 0.2	1 > 0.8
				not A orB, i <— B, i notA_or_Bi 2 <— max' notA,	2>B, 2)	nolAorB =	0.4 0.6	0.65 0.6
			notAorB				0.8 к 1	0.9 1 >

~ ~

Рис. 4. Определение значения A v B

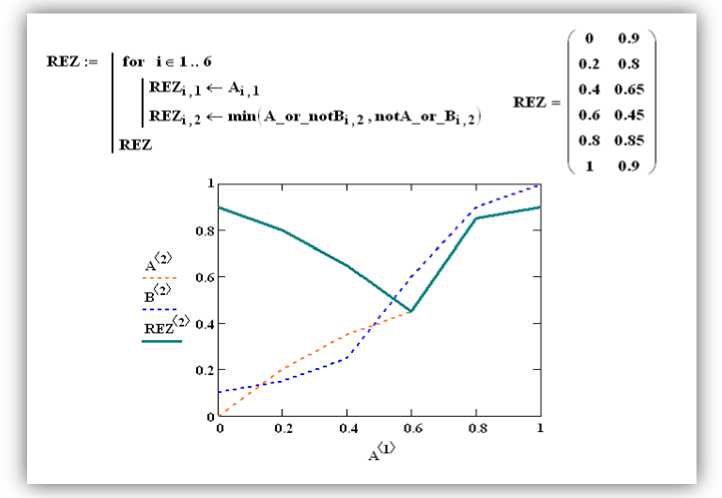
Рис. 5. Вычисление значений конечного результата

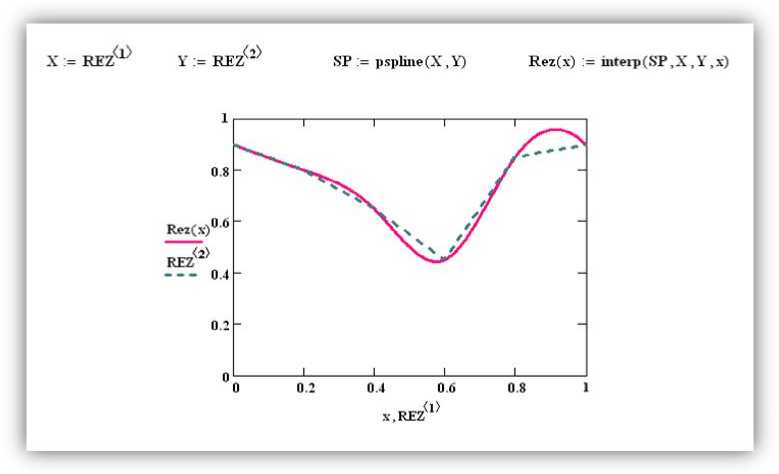
Рис. 6. Интерполяция конечного результата

Нечёткая база знаний

Нечёткой базой знаний называют совокупность нечётких правил «Если – то», определяющих взаимосвязи между входами и выходами изучаемого объекта. Обобщённый формат таких нечётких правил выглядит следующим образом:

если < посылка правила >, то <заключение правила>

Посылка правилa (или антецедент) задаётся выражением типа «Х есть < значение >, где < значение > является термом (лингвистической переменной), заданной в виде нечёткого множества на универсальном множестве лингвистической переменной Х. Для модификации термов антецедента используют квантификаторы «очень», «почти», «более-менее» и т.п. Заключение правила или следствие задаётся выражением типа «Y есть < значение >, где значение выходной переменной может быть задано в виде терма, класса решений, чёткой константы или функции от входной переменной.

Если значение входной переменной правила задано в виде нечёткого множества, то само правило можно представить в виде нечёткого отношения. Для нечёткого правила «Если Х есть А, то Y есть В » нечёткое отношение R задаётся на декартовом произведении U x x U y , где U x (U y ) - универсальное множество входной (выходной) переменной.

Для расчёта нечёткого отношения могут быть применены импликация и t- норма. Если, например, в качестве t- нормы использовать операцию нахождения минимума, то нечёткое отношение рассчитывается следующим образом:

ЦR(x,y) = min(цA(x),цB(y)),(x,y)e Ux хUy (4)

Пример 2 . Нечёткая база знаний описывает зависимость между возрастом человека (V ! ) и возможностью устроиться на работу в условиях кризиса (V₂):

Если V ! = молодой , то V₂ = низкая

Если V₁ = средний , то V₂ = высокая

Если V₁ = старый или молодой , то V₂ = не очень высокая

Предположим, что функции принадлежности термов определены так, как это показано на рисунках 7 и 8. Нечёткие отношения, соответствующие правилам рассматриваемой базы знаний, показаны на рисунках 9-11.

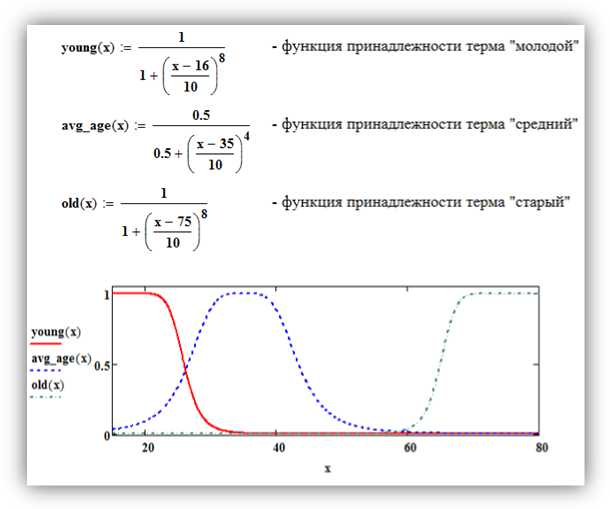
Рис. 7. Функции принадлежности термов возраста

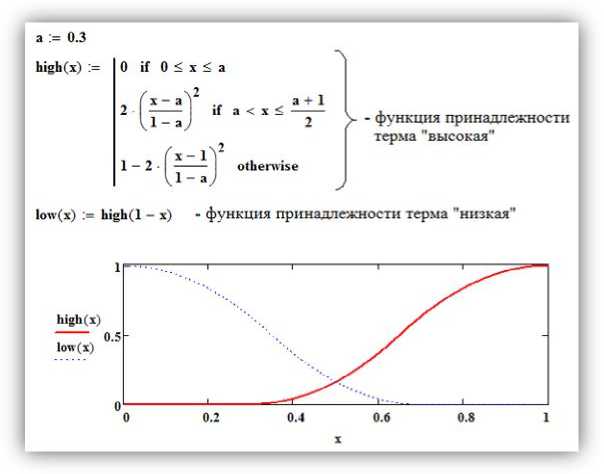
Рис. 8. Функции принадлежности термов возможности устройства на работу

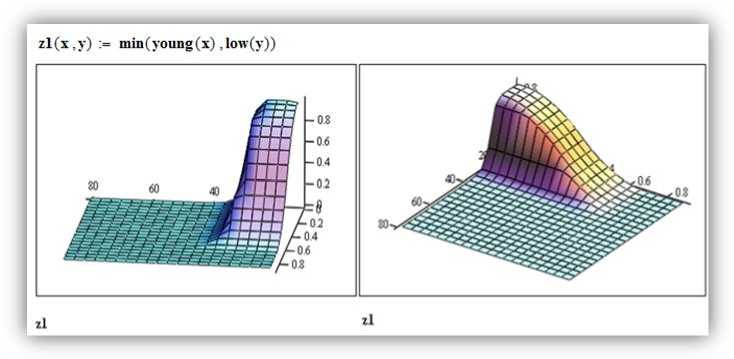
Рис. 9. Отношение «Если V 1 = молодой , то V 2 = низкая »

z2(x,y) := min(avg_age(x) , high(y))

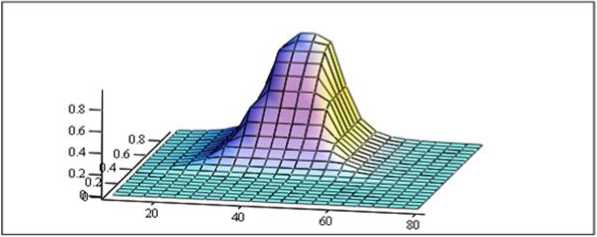
Рис. 10. Отношение «Если V 1 = средний , то V 2 = высокая »

z3(x ,y) := minll - avg_age(x) ,1 - high(y)*)

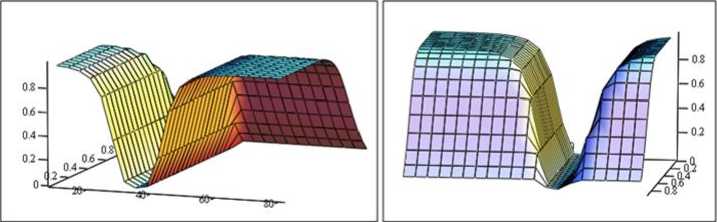
Рис. 11. Отношение «Если V₁ = старый или молодой , то V₂ = не очень высокая »

Заключение

Описанные методы позволяют успешно использовать для решения задач нечёткой логики и теории нечётких множеств такое популярное и распространённое программное обеспечение, как пакет решения математических задач MATHCAD. Ограничения, связанные с использованием этого пакета, требуют принять некоторые соглашения при определении нечётких множеств, а именно: определять нечёткие множества с помощью матриц. С практической точки зрения это оправдано, т.к. основы теории нечётких множеств и нечёткой логики изучаются в рамках небольших спецкурсов, для которых в учебных планах не предусмотрено большое количество контактных часов.