Решение задачи динамики сильно вязких несжимаемых сред и его приложение к моделированию напряженно-деформированного состояния тектоносферы Земли

с вязкостью n ~ 10¹⁹...10 24 Паю. С учетом этих обстоятельств движения тектоносферы могут быть описаны уравнением Навье–Стокса в приближении малых чисел Рейнольдса (Rе << 1) и уравнением неразрывности [1–3], которые в этих условиях существенно упрощаются и в векторной форме имеют следующий вид:

-V p (x) + nV2u (x) + H (x) = 0, (1) V u (x ) = 0. (2)

Здесь x — радиус-вектор расчётной точки среды (в дальнейшем для краткости будем называть его расчетной точкой x или просто точкой x ); u ( x ) — вектор мгновенной скорости смещения среды в расчётной точке x ; p ( x ) — давление в точке x ; H ( x ) — вектор массовой силы в точке x , отнесённый к единице объёма; η — коэффициент динамической вязкости среды; V — дифференциальный оператор «набла»; V ² — дифференциальный оператор «лапласиан».

В подобной постановке решены, как численно , так и аналитически, многие задачи, составляющие основу гидродинамической теории смазки и имеющие большое значение в химической технологии, в биологических и других приложениях. При этом точные аналитические решения получены лишь для случаев, когда границы сред представляются поверхностью или системой поверхностей относительно простой геометрической формы (плоскостью, цилиндром, сферой, эллипсоидом и так далее), что существенно упрощает реализацию задачи. Однако при изучении напряжений, деформаций и мгновенных скоростей вязкого смещения среды в тектоносфере Земли использование этих результатов ограничивается сложностью форм и неоднородностью строения реальных моделей тектоносферы.

В данной работе рассматривается решение фундаментальной системы уравнений динамики сильно вязких сред, соответствующей системе уравнений (1), (2), которое в целом ряде случаев позволяет получить конечный аналитический вид решения задачи для более сложных моделей строения различных областей тектоносферы Земли.

• 2.    Постановка задачи

• 3.    Решение задачи

Требуется найти решение системы уравнений (1), (2) для некоторой произвольной ограниченной области V ( V с E 3 , E 3 — трехмерное евклидово пространство). Рассматривая область сколь угодно большой ( V >  E 3 ) , предположим, что искомые функции u ( x ) и p ( x ) удовлетворяют условиям на бесконечности:

U ( x ) = O ( x| ^{- 1} ) , p ( x ) = O ( x| - 2 ) при |x| >^ ( г = 1,2,3 ) , (3) где |x| = ^x ^ + x 22 + x ₃² — норма точки x , x 1 , x ₂, x 3 — её координаты в декартовой системе Ox 1 x ₂ x 3 ; u ( x ) — z- я компонента вектора u ( x ) . Допустим также, что функция H ( x ) непрерывна вместе со своими первыми производными в некоторой ограниченной области D с V , а вне её H ( x ) ^ 0 . Иными словами, H ( x ) есть финитная функция с носителем supp H ( x ) = D . Кроме того, будем считать, что области D и V ограничены кусочно-гладкими поверхностями 5 D и 9 V .

Получим формальное решение задачи. Для этого возьмём дивергенцию от обеих частей уравнения (1) и, учитывая уравнение (2), будем иметь

V (-V p (x) + n-V2u(x) + H (x))=-Ap (x) + n-V2 (Vu(x))+V H (x) = -V2 p (x)+V H (x) = 0

или

V ² p ( x ) = -V ( - H ( x )) .                                                                (4)

Уравнение (4) является уравнением Пуассона относительно функции давления p ( x ) . Так как выражение V ( - H ( x )) в правой части равно нулю вне области V вследствие финитности функции H ( x ) , а область V ограничена кусочно-гладкой поверхностью 5 V , то решение этого уравнения, удовлетворяющее при |х| ^ да условиям (3) , можно записать в виде

p ( x ) = -y ( 4 n ) J [v H ( X )/ R ( x , X ) ] d - V ,                                          (5)

V где  R(x,X)= |x - X|;  d§V — элементарный объём, содержащий переменную интегрирования X = (^1, ^2, 4;), 4i — значения её координат.

Учитывая тождество

У R (x, X ) = v2 R (x, X)/2, уравнение (5) можно переписать в виде p (x ) = -У (8n)V2 JR (x, X )V H (X )dV.                                            (6)

V

Здесь и в дальнейшем, там, где под операторами V ² и V стоит функция двух переменных x и ξ , дифференцирование будем осуществлять только по переменной x .

Подставляя (6) в уравнение (1), получим

V ²

У( 8 п ) V J R ( x , X ) V H ( X ) dV + p- u ( x ) V

= ^{- H ( x} ) .

Уравнение (7) также является уравнением Пуассона относительно функции, представленной выражением под лапласианом. Так как функция H ( x ) в правой части равна нулю вне области V , а искомая функция удовлетворяет условиям (3) на бесконечности, то решение уравнения (7) можно записать в виде

• У ( 8 n ) V j R ( x , X ) V H ( X ) dV + n- u ( x ) = 1/ ( 4 n ) J [ H ( X )/ R ( x , X ) ] d ^ V .

VV

Отсюда найдем выражение для функции u ( x ) :

u ( x ) = У( 4 nn ) J [ H ( X )/ R ( x , X ) ] d ^ V - У( 8 nn ) v J R ( x , X ) V H ( X ) d ^ V .               (8)

VV

Преобразовав второй интеграл в правой части (8) по формуле Гаусса–Остроградского, получим:

u ( x ) = 1 ( 4 nn ) J [ H ( X )/ R ( x , X ) ] dV - 1 ( 8 nn ) v J H ( X ) V R ( x , X ) dV -

VV

• - 1 ( 8 nn ) v J H ( X ) n ( X ) R ( x , X ) d , S .

d V

Здесь n ( X ) — единичный вектор внешней нормали к поверхности 5 V в текущей точке X ; d ^ S — элемент 5 V , содержащий точку X .

Так как интеграл по 5 V в правой части (9), вследствие финитности H ( x ) , равен нулю, выражение для функции u ( x ) приобретает следующий окончательный вид:

u ( x ) = у ( 4 nn ) J [ H ( X )/ R ( x , X ) ] d , V - У ( 8 nn ) v J H ( X ) V R ( x , X ) d ^ V .              (10)

VV

Выражения (6), (10) являются формальным решением системы уравнений (1), (2).

Представим теперь эти выражения в проекциях на оси системы координат Ox 1 х ₂ х ₃ :

e,(x)-V(4nn)J[Hj^MR(x,^)]dV-1 (8™1)£JHi^-TR2^)dV (j = 1,2,3),(11)

V                                   i=1 V p (x) = -1 (4n)vJ[H (5) R-1 (x,5)] dV = -1/ (4л)£ Aj Hj(^) R (x,5) dV,(12)

V                                    j=1 dXj V где Hj (5) — j-я компонента вектора массовых сил H(5).

Рассмотрим частный случай, а именно действие единичной сосредоточенной силы, приложенной в начале координат и направленной по оси Ox i . Данную силу можно трактовать как распределение массовых сил, определяемых следующей формулой [4]:

H , ( 5 ) = 8 „ 8 ( 5 ) ( i , j = 1,2,3 ) .

Здесь 5j — символ Кронекера, 5(5) — обобщённая 5 -функция Дирака от векторного аргумента. Подставив (13) в (12), получим pi (x)=-1 (4п) t^ f 8, -8(5) ■ R-1 (x,5)ds V=-1 (4n) 8R ' (x,0) (i = 1,2,3)          (14)

j-=1 dxj V                                             dxi и аналогично после подстановки (13) в (11):

. , ,             \ 5 j ,         d² R ( x , 0 )

( i , j = 1, 2, 3 ) .

и (x) = V(4 др )    ^J   -1 (8 др )---------

^А ’          ’ R ( x , 0 ) ^/V ’ d x i dx j

Здесь u j ( x ) — j -я компонента вектора скорости u ¹ ( x ) ; u ¹ ( x ) и p i ( x ) — скорость и давление, обусловленные действием единичной сосредоточенной силы, направленной по оси Ox i и приложенной в начале координат. В общем же случае, когда сосредоточенная сила приложена не в начале координат O , а в произвольной точке 5 , выражения (14), (15) принимают вид:

u i ⁽ x , ⁵ ) = g j ⁽ x , ⁵ )/й , ^где g j ( ^x , ⁵ ) = -У( ^{8 п ) d} R ⁽ x⁵ ) + У ( 4 ^{п )}3- ,        ⁽¹⁶⁾

d X j d X i             r ( x , 5 )

p i ⁽ x , ⁵ ) =- v ^{( 4 n)}d x - [ R c x : 5 ) ] •                                                    ⁽¹⁷⁾

Формулы (16), (17) представляют собой решение так называемой фундаментальной системы уравнений [5], отвечающей системе (1), (2):

pi (x, 5 ) + n2u1 (x, 5 ) + 5( x - 5) i = 0, ui( x, 5 ) = 0, где i — i-й орт декартовой системы координат Ox 1 х2 х3. Это решение, как несложно заметить, удовлетворяет условиям:

u j ( x , 5 ) = O ( R ^{- 1} ( x , 5 ) ) ,     p i ( x , 5 ) = O ( R "² ( x , 5 ) )     при R ( x , 5 ) ^« .

Поскольку по условиям задачи внешние силы H ( x ) распределены в ограниченном объёме D , где D с V , решение системы уравнений (1), (2) можно записать в виде:

u ( x ) = (V n ) J G ( x , 5 ) • H ( 5 ) dV ,                                                 (18)

D

p ( x ) = J P ( x , E ) • H ( E ) d , V ,                                                            (19)

D где G(x, E) — симметричная квадратная матрица третьего порядка, элементами которой являются величины     gj (x, E),    представленные формулой (16), а

P ( x , E ) = ( p ¹ ( x , E ) , p 2 ( x , E ) , P 3 ( x , E ) ) — трёхмерный вектор, компоненты которого p‘ ( x , E ) определяются выражением (17). При этом в окрестности бесконечно удалённой точки решения (18), (19) удовлетворяют условиям:

u i ( x ) = O ( |x |^-1 ) , p i ( x ) = O ( |x |^-2 ) при     |x | >^ .

Несложно показать, что если граница 5 D объёма D является достаточно гладкой и удовлетворяет условиям А.М. Ляпунова [6], а функция H ( x ) непрерывна по Гельдеру [7] в области D c параметром а (0 <а< 1), то полученное решение (18), (19) системы уравнений (1), (2) существует и единственно. Однако из-за ограничения объёма статьи доказательство этого факта здесь опускаем.

• 4.    Формулировка задачи моделирования тектоносферы

Выберем декартову систему координат Ox1x2x3 таким образом, чтобы ось Ox3 была направлена вертикально вниз. Возьмём в качестве неограниченной области V с E3

полупространство x ₃ >  0. Будем полагать также, что плоскость x ₃ = 0 совпадает с поверхностью Земли (выпуклостью земной поверхности пренебрегаем), а ось Ox ₃ , следовательно, направлена к центру Земли перпендикулярно её поверхности. В этом же направлении, как известно, действует вектор силы тяжести g = g • i₃ , где g = |g| = 9,8 м • с ^{- 2}, а i₃ — орт оси Ox ₃. Кроме того, предположим, что полупространство x ₃ >  0 (толща Земли) заполнено сильно вязкой однородной (в смысле вязкости) несжимаемой средой, и движение этой среды происходит в однородном гравитационном поле Земли. При этом вектор массовых сил H ( x ) определим выражением H ( x ) = р ( x ) • g = р ( x ) • g • i₃ = H 3 ( x ) • i₃ , где Н ₃ ( x ) — компонента вектора H ( x ) , направленная по оси Ox ₃, р ( x ) — плотность среды.

Положим р ( x ) = р ₀ ( x ) + Ар ( x ) , где под р ₀ ( x ) понимается некоторое механически равновесное распределение плотности Земли [8, 9], изменяющееся только вдоль оси Ox ₃ ( р ₀ ( x ) = р ₀ ( x ₃ ) ), а под Ар ( x ) понимается так называемое аномальное распределение плотности. Равновесному распределению плотности отвечают следующие выражения для вектора мгновенной скорости смещения среды u ₀ ( x ) и равновесного давления p ₀ ( x ) :

x ₃

u0(x) = 0, p0 (x) = J gр0 (E3)dE3. Так как распределение плотности р(x) отлично от равновесного р0 (x), то и давление p(x) также будет отличным от равновесного давления p0 (x). Назовём аномальным давление Аp(x) , вычисляемое с помощью выражения

^А p ^{( x )} = p ^{( x )-} p 0 ^{( x )} .                                                                    ⁽²⁰⁾

Аналогично обозначим как A u ( x ) аномальную скорость смещения среды:

A u ( x ) = u ( x ) - u ₀ ( x ) .                                                                    (21)

Отсюда p (x) = p o(x) + Дp (x),       u(x) = Uo(x) + Au(x).(22)

Запишем выражение для массовых сил H ( x ) более подробно, с учётом того, что р ( ^x ) = Р о ( ^x ) ^{+ Д}р ( ^x ) ^:

Н ( x ) = р( x )• g • i3 =(ро ( x ) + Др( x ))• g • i3 = Ро ( x )• g • i3 + Др( x )• g • is .

Полагая H ₀ ( x ) =р ₀ ( ^x ) ^ g - i s и ^{Д Н} ( ^x ) = ^ДР ( ^x ) • g • i₃ , запишем выражение (23) в виде:

Н (x) = Но (x) + ДН (x),(24)

откуда

АН(x) = Н(x)-Но (x),(25)

где Н _о ( x ) назовём равновесным, а Д H ( x ) — аномальным распределением массовых сил.

Подставив выражения (22), (24) для функций p ( x ) , u ( x ) и H ( x ) в уравнения (1), (2), получим новую систему

• -V (Дp (x)) + nV2 (Au (x)) + АН (x) = о,(26)

• V (Дu (x )) = о,(27)

• 5.    Решение задачи моделирования

  

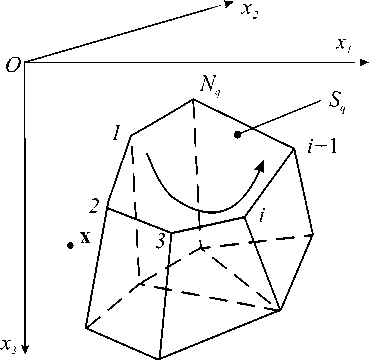
  Рис. 1. Многогранник D_Q ( S_q – q -я грань многогранника, x – расчётная точка; стрелкой показано направление обхода точек грани при нумерации)

  
  

из рассмотрения которой видно, что здесь, в отличие от системы (1), (2), вместо функций p ( x ) , u ( x ) и H ( x ) присутствуют их аномалии Д p ( x ) , Д u ( x ) и Д H ( x ) , понимаемые в смысле выражений (20), (21) и (25). Так как в дальнейшем изложении всегда вместо функций р ( x ) , p ( x ) , u ( x ) , H ( x ) будем рассматривать их аномалии, то значки аномальности Д опускаем. С учётом этого система уравнений (26), (27) становится совпадающей по виду с системой (1), (2), но под p ( x ) , u ( x ) , Н ( x ) понимаются уже не сами эти функции, а их аномалии. На основании вышеизложенного решение такой системы определяется соотношениями (18), (19), в которых полагается Н ( ^x ) = p ( ^x ) • g 43, где р ( x ) — аномальная плотность, а Н ( x ) — аномальные массовые силы.

При проведении численных расчётов любое аномальное по плотности геологическое тело (любую неоднородность тектоносферы) удобно аппроксимировать с помощью системы элементарных тел (многогранников), имеющих постоянные значения аномальной плотности р(x). Покажем, что компоненты скорости смещения среды и давление, обусловленные влиянием таких тел в гравитационном поле Земли, могут быть выражены в явном виде. Для этого рассмотрим многогранник произвольной формы, расположенный в полупространстве x3 > о (Рис. 1). Обозначим его как DQ, где Q —

Q число граней Sq, а dDQ = ^ Sq — поверхность, q=1

ограничивающая DQ . Грань Sq представляет собой плоский многоугольник, имеющий Nq вершин. При этом вершины такого многоугольника считаются пронумерованными в положительном направлении, если при движении по ограничивающей его ломаной линии дSq область Sq остается слева.

Аномальную плотность ρ многогранника D_Q будем считать постоянной.

Тогда, при условиях, сформулированных в предыдущем разделе статьи, соотношения (18), (19), дающие общее решение задачи, преобразуются к виду:

u j ⁽ x ) = ^P" g f g" ( x ^ ) ' h ^{( 5} ) d 5 V , ⁿ D Q

P ( x ) = P- g f P 3 ( x , ⁵ ) • h 3 ( ⁵ ) d 5 V ( j = 1, 2, ³ ) .

D Q

Подставив в (28) выражение для g j ( x, ^ ) из (16), получим:

uj

( x )=^ f g j ( x , 5 ) d _t V -8 nnJ

DQ

ⁿ D

Q

д² R (x,5) ,       5_/3 ,     1

---(-^ d ₅ V +   [ —--- d ₅ V = д x ₃ д x j    ^     4n D R (x, 2)  ^

l g f ^{8 п}П д D Q

Y( 5 ^^ 5 S +^ (

¹ d _ξ V ,

R ( ^x , 2 )

где у (5) — косинус угла между осью Ox3 и вектором внешней нормали к дdq , а интеграл        dξV представляет собой гравитационный потенциал однородного

D_Q R ^{( x} , ^ )

многогранника; его аналитическое выражение приведено в работах [10, 11].

Для расчета первого интеграла в правой части (29) воспользуемся вспомогательными ортогональными системами координат O2q 22 2q, связанными с гранями Sq многогранника DQ соотношениями

( 5 q ) ^T = м q ( 5 - x ) ^T,      5 q = (y , 2 2 , 2 f )      ( q = 1,..., Q ) .                            (30)

Здесь T — знак операции транспонирования; M _q — ортогональная матрица преобразования (30), такая, что в новой системе координат плоскость, несущая грань S_q , имеет уравнение 2 2 = const, а угол между осями O 2 2 и Ox ₃ не превышает п/2. Если в системе координат Ox 1 x ₂ x ₃ грань S q задается уравнением A q x 1 + B q x₂ + C q x₃ + D q = 0, то выражение для ортогональной матрицы М _q имеет вид:

^М q =

— ^B2 D 2 /( Г 2^2 й

- A q CD q К r q R q D . 1) A q C q R q C q

A q D q /( r . D . I)

- B q CD qk RM

B q C q R q C q

r q C q D q r q R q D q C q R q

где r q = 7 ^Aq + B q ,

^R _q = AA + + B_q ² + C q . Очевидно, что имеют место и обратные к (30) преобразования координат:

( 5 - x ) ^T = M T ( 5 ^q ) ^T.                                                                    (31)

Применяя соотношения (30), первый интеграл в правой части (29) преобразуем к виду:

f y ( 5 )^ ^R 2-^{x , 5} ) ^d . S = ]T Y q |5 j Z x L d 2 q d 2 2    ( j = ^1,2,3 ) ,                       (32)

д D Q           ^д2 j           q = 1 s _q R ^{( x} , ⁵ )

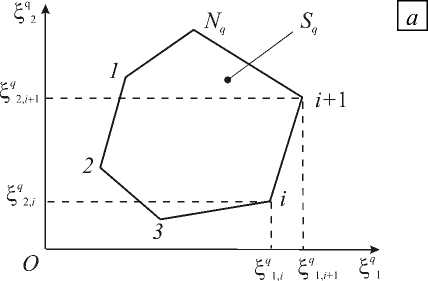
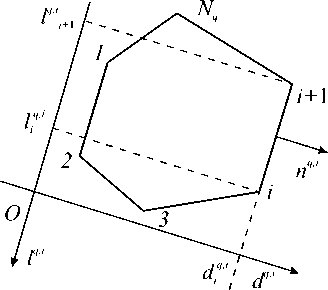
Рис. 2. Грань S_q многогранника D_Q в связанной с ней ( а ) и во вспомогательной ( б ) системе координат

б

где у q = C q / ^ q — косинус угла между положительным направлением оси Ox 3 и вектором внешней нормали к грани S _q многогранника D _Q . Расположение грани S _q в координатной плоскости O E q E q системы координат O E q E q E q приведено на рисунке 2, а .

Используя соотношения (31), определим интеграл в правой части (32):

E- x

jjqq qqqqqq

J            ^{Е 1 Е} 2 m j ¹ J Rd ^Е 2 m j 2 J Rd ^E 1 ⁺ m j 3 ^E 3 ^Q q ( ^X ) ,

Sq R ( X, ^ )                   gSq               gSq где R = R(x,E) = R(Eq) = J(Eq) + (Eq) + (Eq) , m‘q — элементы матрицы МT = m'q ,       123, jk            qjk

( j , k = 1,2,3 ) , а Q q ( x ) = J ( 1 R ) d E q d E q представляет собой потенциал грани S _q .

S q

Величина R = ^( E q ) + ( E q ) + ( E 2 )

является инвариантной относительно ортогонального

J Rd E q a s q

преобразования координат системы OEq Eq, поэтому вычисление интегралов и J Rd Eq в правой части (33) удобнее выполнять во вспомогательной координатной

8Sq системе Ol4, idq, ', получаемой поворотом системы OEq Eq вокруг ее начала O таким образом, чтобы направление оси Od q,i совпало с направлением вектора внешней нормали nq’' к i-му отрезку ломаной 5Sq, соединяющему '-ю и (i + 1)-ю вершины многоугольника Sq (Рис. 2, б). При этом координаты точек отрезка оси Od q,i сохраняют постоянство (df, i = const), а значения lq, i и dq, i определяются по формулам l* ,'= mq;-Eq + mqa-Eq, dq ,‘= mqi E + mn-E?, ■ Здесь m« =(E^1,-Eu+1) Jk, mq, =(E!i-Eq,i.i)/k, m q1i=-(E2,i-E2.,+.)/k, m*!i=(E*,i-E*i+1) /k,

k=^Ei

-E q, + 1 ) ² + ( E 2, i -E q , i . i ) ²,где E q , i , E q,

— координаты i -й вершины многоугольника

S q ( i = 1,..., N q + 1 ), E q _{Nq + 1} =E ₁ q ₁, E q , _{Nq + 1} = E q , ₁, а компоненты вектора нормали n q , i связываются со вспомогательными координатами следующими формулами: n , ' = - ( E 2, i -E 2, i + 1)/ k , n q , ' = ( E q , , -E q , i . 1)/ k .

Тогда в новой системе координат первый интеграл в правой части (33) определится следующим образом:

N q ^ q , . ₊ 1

J Rd eq = Z J Rd eq,

SSq                   ' ' 52,, qq,

52,+i                        l2i+i                                                                qi где

J Rd52 = nqi J (jqlqi)2 +(d,,)2 +(yq)2diq4 = n^{R• iq, +1 (d,,)2 +(yq)2 lln(R+lqi)} eq,,                У                                         2

l qi = i qi p i = iq,‘

Аналогично находим интеграл J Rd y q .

a S q

На основании формул (29)–(34) получим аналитическое представление для компонент U j ( x ) вектора мгновенной скорости смещения среды u ( x ) :

j ’b-S

Q   N q    qq ,

Z r q Z q = 1 i = 1

- m^

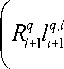
- Rqlq,'+[(d ^ +(5q )2

/<•-/-

+ i q ,i

q

+m4 Qq +5j3 •y3 Q (x)

( j = 1,2,3 ) ,

где выражение для потенциала Q _q ( x ) q -й грани S_q многогранника D Q имеет вид [10, 11]:

Q ^N q          R q - i q,i       (          i q - i>q              i q,i             i q - i' y q              i q, A

Q, ( x ) = Y Y i ^q,! In ——— +5 q arctg i ^{+ 1 3} — arctg — 1-- arctg i . ³ + arctg— ^{q V 7} Z = 1 ^Z ‘      R i + i q ,      I       d ^q , ' R +          d^ q ,¹        ddf , ‘Rqi        ddi ,¹ J

Подставив в формулу для давления из (28) выражение (17) для p ³ ( x,^ ) и приняв во внимание, что Q ( x ) = [— d ^ q d ^ q , найдем выражение для давления p ( x ) :

q     R 12

Sq

/ \ _  Рg f d    1 ,УК Jt! Jt! _ Pg V v f d ^qd5q - Pg Vv О M p ( x )=            d/ e\d 51 d52d53 = о ZY ql р/ e\   л ZY qQ q (x) .

4 n D Q d x 3 R ( x , ^ )                8 nn q : 1 ^q S q R ( x , ^ )    4 n q = 1

Компоненты тензора напряжений вычислим по формулам

^T j ( ^x ) = n ( ^{d u}i ( . x )/^d x j ^+d u j ( ^x )/^d x ) ^- 5 j P ( x )       ( г , j = 1,2, 3 ) .

• 6.    Результаты

Полученные в явном виде выражения характеристик геомеханического состояния сплошной сильно вязкой несжимаемой среды (35)–(38) использовались далее для расчета напряжений и векторного поля мгновенных скоростей смещения в тектоносфере Земли при наличии в ней некоторого аномального включения.

На рисунке 3 приводятся результаты вычисления вертикальной и тангенциальной компонент тензора напряжений, а на рисунке 4 — поле мгновенных скоростей смещения среды, обусловленных влиянием аномального тела, представляющего собой горизонтальную призму с сечением в форме равнобедренного треугольника. Вязкости вмещающей среды и самого тела считались постоянными и равными п = 10 19 Па • с, плотность аномального тела равнялась р = 20 кг/м³ . Горизонтальное основание призмы располагалось на глубине 380 км перпендикулярно направлению вектора ускорения силы тяжести g . Размеры призмы составляли: 500 км по оси Ох 1 , 250 км по оси Ох 3 , 1000 км по оси Ох 2 (ось Ох 2 перпендикулярна плоскости рисунка и направлена от зрителя). Вычисления характеристик среды проводились в плоскости симметрии аномальной призмы ( х 2 = 0).

О 100 200 300 400 500 600 700 800

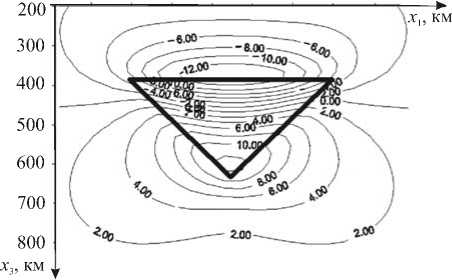
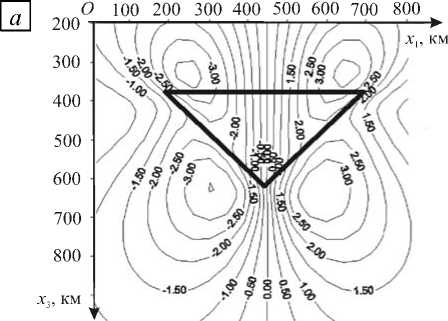
Рис. 3. Изолинии вертикальной τ ₃₃ ( а ) и тангенциальной τ ₁₃ ( б ) компонент тензора напряжений (МПа),

б

возникающих в тектоносфере при наличии в ней призматического аномального включения

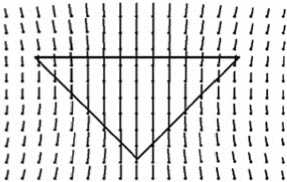
Рис. 4. Распределение векторов мгновенной скорости смещения u ( x ) среды, имеющей вязкость η = 10¹⁹Па ⋅ с ; u _max = 8,7 м/год

• 7.    Заключение

Используя различные композиции из элементарных аппроксимирующих тел (многогранников) можно со сколь угодно большой точностью построить модель тектоносферы Земли и рассчитать ее напряженно-деформированное состояние. Так как в данной работе решение задачи получено в конечном виде, его точность будет зависеть только от точности аппроксимации, погрешности исходных данных и ошибок округления. Однако предположение однородности по вязкости у аномального по плотности включения и вмещающей его среды — тектоносферы в определенной мере сужает область практической применимости полученных результатов. Вместе с тем аналитическое решение подобной задачи имеет и самостоятельное теоретическое значение.