Решение задачи градиентной термоупругости для цилиндра с термозащитным покрытием

покрытия, у которых термомеханические свойства не константы, а функции координат [1]. При их применении скачки материальных свойств на поверхности раздела «покрытие–подложка» отсутствуют.

Наиболее распространенным методом исследования состояния неоднородных тел является метод конечных элементов [2]. Используются и другие приближенные методы. Так, в работе [3] предложен экономный численно-аналитический метод решения задачи термоупругости для вытянутого прямоугольника, состоящего из теплозащитных покрытий двух типов — однородного и функциональноградиентного. Для каждого типа покрытия представлена своя модель термоупругого деформирования системы «покрытие–подложка». В основу моделей деформирования положены специальные законы распределения компонент вектора перемещений и температуры по толщине покрытия, позволившие учесть влияние неоднородности термомеханических характеристик, удовлетворить условия сопряжения полей перемещений, напряжений, температуры и теплового потока. Неизвестные функции, входящие в выражения для трансформант температуры и перемещений, определялись с помощью вариационного принципа термоупругости и метода Канторовича.

При расчетах напряженного состояния в микроразмерных объектах применяется градиентная теория упругости. В этой теории учитываются масштабные эффекты, то есть зависимость напряженно-деформированного состояния (НДС) от характерных размерных параметров. Градиентная теория упругости, сформулированная в середине прошлого века в работах Тупина [4] и Миндлина [5], в дальнейшем получила свое обобщение на теорию термоупругости [6].

Впервые задача Ламе с позиций градиентной теории упругости рассмотрена в [7] для трубы бесконечной длины и сферической оболочки, которые находятся под действием равномерного внешнего и внутреннего давления. Однако практическое использование модели Тупина–Миндлина натолкнулось на вопрос об идентификации 5 дополнительных градиентных модулей. В целях упрощения определяющих уравнений были предложены прикладные градиентные модели Айфантиса [8–11] и Лурье [12], в определяющие уравнения которых включается только один градиентный параметр. В рамках однопараметрической модели Айфантиса в работе [13] на основе вариационного принципа получены уравнения равновесия и граничные условия задачи о равновесии однородного толстостенного полого цилиндра при механическом нагружении, найдено аналитическое решение задачи с помощью аппарата модифицированных функций Бесселя. Аналитические решения получены и для задачи определения НДС неоднородного полого цилиндра при степенных законах неоднородности теплового и механического нагружений [14–16].

Однопараметрические градиентные модели механики применяются и для уточнения НДС слоистых упругих [17–20] и термоупругих [21, 22] тел. В [17] в рамках модели межфазного слоя С.А. Лурье численно исследуется равновесие слоя с покрытием под воздействием локализованной нормальной нагрузки. Решение получено с использованием интегрального преобразования Фурье и его численного обращения. В работе [20] решается задача изгиба микробалки с частичным покрытием. Исследовано влияние изменения величины масштабного параметра на характер распределения в балке смещений, напряжений и на положение ее нейтральной линии. В предположении об одномерности задачи в [21] аналитически исследуется НДС тонкослойных композитных структур при тепловом воздействии. Авторами [22] решена задача градиентной термоупругости для составного стержня, при этом для нахождения напряжений Коши применен асимптотический подход Вишика–Люстерника, учитывающий наличие погранслойных решений в окрестности границ и точки сопряжения стержней. Также исследована зависимость скачка напряжений Коши от соотношения физических характеристик стержней и масштабного параметра.

Целями данной работы являются: постановка задачи градиентной термоупругости для полого цилиндра с термозащитным покрытием при эффективном обезразмеривании; выделение на основе асимптотического метода Вентцеля–Крамерса–Бриллюэна — метода ВКБ, погранслойных частей решения; использование метода пристрелки для решения задачи термоупругости в классической постановке; тестирование метода решения на примере однородного покрытия; вычисление радиальных перемещений, напряжений Коши, полных и моментных напряжений как для однородного, так и неоднородного покрытия; анализ полученных результатов.

• 2.    Определяющие соотношения градиентной механики

В градиентной теории упругости плотность энергии деформации зависит не только от деформации, но и от ее первого градиента [5]. В случае линейного изотропного материала выражение для плотности энергии деформации в рамках однопараметрической модели Айфантиса имеет вид [8]:

w = (V 2 )⁸ ii ⁸ jj + ^ц8 b y + l ² ( ( X/ 2 ) e,. _k ⁸ jj,k + ^ц8, k b y , k ) , ⁽¹⁾

где X и ц — параметры Ламе, 8j — компоненты тензора деформаций, l — градиентный параметр, который характеризует микроструктурное строение материала и имеет размерность длины (например, для поликристаллических тел — это размер зерна).

В градиентной теории упругости компоненты тензора напряжений Коши т _у , тензора моментных напряжений m_ijs , тензора полных напряжений ° представляются в виде:

m js

СУ - — T - — j j

dw т.. =,

*j^

5w,

= я-----= 1 т у, s , д8У, s mijs,s =(1 - 12V2 )ту .

Математическая постановка задачи градиентной термоупругости включает [6]: – уравнения равновесия, записанные в полных напряжениях

° у , j = 0 ;

– механические статические граничные условия тjnj - mijs,snj - (mijs,sns ),у + (mijs,snjns ),z nz = ti ,     mijs,snjns = Pi ;

– механические кинематические граничные условия dv u = v,    «У nj= л-;

d n

– классическое уравнение теплопроводности

(kуT,i)_j= 0;(8)

– тепловые граничные условия 1-го рода, заданные на поверхности S_T

T\sT = To;(9)

– тепловые граничные условия 2-го рода, заданные на поверхности Sq qs = qo.(10)

Sq

Здесь: t i , p i — компоненты векторов сил, заданных на поверхности тела; n — компоненты единичного вектора нормали к поверхности тела в рассматриваемой точке; T — температура; k_ij — компоненты тензора теплопроводности; q — тепловой поток; S = S_q U S T — поверхность тела; V — оператор набла (дифференциальный оператор Гамильтона); запятая в нижнем индексе означает дифференцирование по координате.

В полярной системе координат выражения для ненулевых компонент тензоров (2)–(4) и компонент векторов (6) имеют вид [14, 15]:

т rr =(Х + 2ц) dur- + Х u^-Y T, dr     r u    du тфф =(^ + 2ц)^+^^”УT, r     dr m =i2 dlrL,    m   =/2 dl^L, rrr      dr         wr       dr 1 /2 (trr   ТФФ ) mr фф   m ф r ф   2        r     , °rr =Trr — rdr (rmrrr ) + r (mфrф+ mrw) , °ФФ =ТФФ- rdr ( rm фф r )-r ( m ф r Ф+ mr ФФ) tr = T rr - ^If (rmrrr ) + r ( mW r + mф rф + mrW ) ,    P r = mrrr .

Здесь у — коэффициент температурных напряжений.

• 3.    Постановка задачи градиентной термоупругости для цилиндра

Рассмотрим бесконечно длинный термоупругий цилиндр, на внешнюю боковую поверхность r = h _l которого нанесено термозащитное покрытие толщиной h . На внутренней боковой поверхности цилиндра r = a поддерживается нулевая температура. Внешняя поверхность покрытия r = b , где b = h + h , свободна от напряжений и находится при температуре T ₀ . Материал цилиндра однородный, характеризуется коэффициентами Ламе X _l и ц , коэффициентом теплопроводности k_l , коэффициентом температурных напряжений y _l. Материал покрытия имеет характеристики Х ₂, ц ₂ , к 2 , у 2 , зависящие от координаты r . Представим материальные характеристики системы «цилиндр–покрытие» в виде кусочно-непрерывных функций:

, .    I F, = const,

F ^{( r} ’ =1 F 2 ( r ) .

при r е [ a , b ] , при r е ( b , c ] ,

где в качестве F ₁ (или F ₂ ) может выступать любая из материальных характеристик цилиндра (или покрытия).

Согласно классической постановке задачи на поверхности сопряжения покрытия и цилиндра r = h , должны выполняться условия непрерывности по температуре, тепловому потоку, перемещениям и радиальным напряжениям. Поскольку уравнения равновесия в градиентной теории имеют повышенный по сравнению с классической теорией порядок дифференциальных уравнений, то зададим дополнительные граничные условия и условия сопряжения. В качестве дополнительных условий положим: 1) равенство нулю моментных напряжений на боковых поверхностях цилиндра; 2) непрерывность градиентов перемещений и моментных напряжений на поверхности сопряжения цилиндра и покрытия r = h , [13]. Для упрощения расчетов градиентный параметр будем считать одинаковым для покрытия и цилиндра, то есть 1 1 = 1 2 = 1 . Таким образом, постановка краевой задачи термоупругого деформирования цилиндра с покрытием примет вид:

d ^C rr + dr

C -C rr фф = 0

СУ = T rr rr

- 1 ²

Q = T фф фф

- 1 ²

r d 2 т rr dr1

r e [ a , b ] ,

₊ l d т rr ₉ ^(т rr + 2 r dr

т ))

фф/

,

f d\    Ad т     (т, фф + l фф 2 dr2   r dr

' ФФ

,

= 0,

r e [ a , b ] ,

T ^{( l )}( a ) = 0,      T ^{( 2 )}( b ) = T 0 ,      T ^{( l )}( h _l ) = T ^{( 2 )}( h^ ,

ST ^{( 1 )}               <27^

k l ( h l ’ ^T- ( h l ) = к 2 ( h l )^^ ( h l ) , d r               d r

t® ( a ) = 0,

P r ¹’ ( a ) = 0 ^,

u(1)(hl ) = u(2)(hl),     du— (hl ) = du— (hl), drdr

t r ²’ ( b ) = 0, р Г ²⁾ ( b ) = o,

^( h l ) = t ( 2 ’ ( h l ) ,

P r ( h i ) = P ⁽ r ²⁾( h l ) .

Обезразмерим задачу (12)–(19) согласно формулам:

г и _ с _ r               _{r                 rr}

^ в , U в ,   “ L rr          , Ь^ФФ b        b          Ц0

C          т

ФФ Cf _ ^т rr

, ^ rr ,

Ц 0            Ц с

^ фф

т фф

,

Ц 0

M = m rrr- .   M_w r =

Цо b r=A Rо = hb

Y о            b

m r м

Цоb ’     rw во    Y T

Ц _о

m r

Ц о b ’

l a = —. b

I, = t- .

Ц о

a a = b ’

p =2^ , w = T , k = A . ^r   Ц о b          Т о          k о

k 0 = max

r e [ a . b ]

k ( r ) . Ц о = max ц ( r ) . r e [ a , b ]

В безразмерном виде задача (12)–(19) будет следующей:

d Q rr d C

Q -Q           , ,

+ rr , ^w = о. Ce [ a .1 ] .

Й rr = S rr -

^M    S ФФ

a 2	d 2 S rr , 1 dSrr   т( S rr   S фф ) +        2
	1 d C 2	c d c         C 2     J
a 2	' d 2 s.	1 dS фф - 2 ( S ФФ - S rr ) J
	v d C 2	C dr         C 2 J

— fC k (C) ^ W ) = о. C^e [ a .1]. d CC ^V d C)           ^{L J}

W ⁽¹⁾ ( a ) = о .

т -   - Ц

- = —, ц = —,

Ц о          Ц о

Y o = max у ( r ) . r e [ a , b ]

W(2)(1) = 1.    W(1)(Rо ) = W(2)(Rо).    ki (Ко )^^(R^ ) = k2 (Rо )^(R^).(24)

tr(1) (a ) = о.     tr(2) (1) = о.(25)

p (1) (a ) = о.     p r (1) = о.(26)

U  , R о ) = U ( R ) . dU.  ( R о ) = dU  ( R о ) .     t r ⁽¹⁾( R о ) = t r  ( R о ) .     p A R о ) = P r ²⁾( R о ) . (27)

d C          d C

При этом безразмерные напряжения Коши запишутся как

S rr = ( - + 2 ц ) dU + - U -в о Y w .    s _фф= ( х + 2 ц ) U + X dU -в о Y W .              (28)

' d ^      ^                                     c,       d c,

4. Решение задачи

Решение задачи несвязанной термоупругости (20)–(27) начнем с нахождения радиального распределения температуры в цилиндре и покрытии. Оно следует из решения задачи теплопроводности в классической постановке (23), (24) и имеет вид:

w ⁽¹⁾( C ) = C i f l ( C ) . w ^{( 2 )}( c ) = c 2 f 2 ( c ) + c 3 .

В формуле (29) f 1 ( C ) = [ -d n— . f 2 ( C ) = (   d П _x . C 1 = C ₂ = ,  _x 1 ----tv . C 3 =    , ^{f (} R ^о) , _x .

I n k i ( n )             j j, П k 2 ( n )                f l ( ^R о ) + ^f 2 ( 1 )          f l ( ^R о ) + ^f 2 ( 1 )

После определения температуры приступим к отысканию перемещений и напряжений, которые, согласно [8], можно представить в виде суммы решения задачи термоупругости в классической постановке и дополнительных градиентных слагаемых: U = U_clas + U_grad .

Полагая в (2G)-(27) a = о. придем к классической постановке задачи, которая в случае неоднородного материала покрытия может быть решена только численно. Воспользуемся для этого методом пристрелки [23]. После некоторых преобразований получим каноническую систему двух неоднородных обыкновенных дифференциальных уравнений 1-го порядка относительно радиальных перемещений U _clas и радиальных напряжений Q _clas :

W  —¹—Q----- U +—^Y—В

U clas Г" ,_ⁱⁱclas         __\ „ U clas ^{+         в}о ^W

- + 2 ц ( - + 2 ц ) С - + 2 ц

Q', clas

= ¹ 1   — 1 |q

C(X+ 2 ц J

+41- + 2 Ц      | U_cta ^-М^-— 1 |во W .

C ² (        - + 2 ц) ^clas А- + 2 ц J

а также граничные условия:

Й clas ( a ) = 0,      Й clas ( 1 ) = 0.

Согласно методу пристрелки, решение краевой задачи (30)–(32), описываемой неоднородной системой обыкновенных дифференциальных уравнений, можно представить в виде суммы решения неоднородной задачи Коши (30), (31) с нулевыми начальными условиями на внутренней поверхности: U 01 ) ( а ) = 0, Q 0 ¹ ) ( а ) = 0, и решения однородной задачи Коши (30), (31) с ненулевыми начальными условиями на внутренней поверхности: U 1 ^{( 1} ) ( а ) = 1, О ^{( 1 )} ( а ) = 0, умноженной на коэффициент p :

Й clas ф = Q 0 (^) + p fi ф ,   U^ ф = U 0 ф + pU 1 ф .

При вычислении пар ( U ₀ ( £ ) , Q ₀ ( £ ) ) , ( U 1 ( £ ) , Q 1 ( £ ) ) в случае функций F ( £ ) , не имеющих разрывов 1-го рода, используем стандартные процедуры метода Рунге–Кутты 4–5 порядка точности. Неизвестную константу p определим из начального условия на внешней боковой поверхности цилиндра:

Й clas ( 1 ) = Й 0 ( 1 ) + Р fi ( 1 ) = 0.

При наличии у функций F ( £ ) разрыва 1-го рода на поверхности £ = R ₀ осуществим решение задач Коши на отрезке [ a , R ₀ ] , затем найденные решения в точке ^ = R ₀ зададим как начальные условия для дополнительных задач Коши, которые затем решим на полуинтервале [ R ₀;1 ) .

Имея решение задачи термоупругости в классической постановке, приступим к нахождению дополнительных градиентных слагаемых при малом значении параметра а на основе асимптотического метода ВКБ [23]. Для этого вначале составим уравнение равновесия в перемещениях, подставив в (20) выражения для полных напряжений (21), (22), в которые входят напряжения Коши (28). Рассмотрим однородное уравнение равновесия в перемещениях, которое будет представлять уравнение 4-го порядка с переменными коэффициентами и малым параметром при старшей производной. Согласно [24], ВКБ-решение будем искать в виде:

U grad (10 = D ( ^ ) e g

' а

Выполним разложение функций D ( £ ) и g ( £ ) по параметру а :

D ( ^ ) = D 0 ( ^ ) + D (0 а ¹ + D 2 (0 а ² + D 3 (0 а ³ + ..., g (0 = g 0 ( ^ ) ⁺ g 1 (0 ^а 1 ⁺ g 2 (0 ^а 2 ⁺ g 3 (0 ^а 3 ⁺ ....

Подставим (34) в уравнение равновесия (20) с учетом выражений (35). Группируя слагаемые при одинаковых степенях а , получим последовательность задач, решая которые найдем

D 0 С0 =

( Х ( ^ ) + 2 ц ( ^ ))Л

и два значения g ₀ (0 в виде: g ₀ (0 = ^ и g ₀ (0 = -^ . Тогда выражения

для градиентной части перемещений цилиндра и покрытия, в силу линейности задачи, представим по параметру а как линейную комбинацию двух ВКБ-решений:

U grad со=

( X 1 ( ^ ) + 2 ^ 1 ( ^ ))7 f

( B 1 e + B 2 e ,,     U g 2 ad (0 =

( X ₂ ( ^ ) + 2 ^ 2 (^)У^

( B ₃ e -^^а+ B 4 e ^^/а ) . (36)

В формуле (36) константы B ₁ , B ₂ , B ₃ , B ₄ находятся путем удовлетворения граничных условий (26), (27) для моментных напряжений и градиентов радиальных перемещений. Составляются выражения: M_rrr = а ² S' _r r , где S r'r = fi clas + fi grad . Градиентная добавка для радиальных напряжений определяется по формуле: ^fi grad = ( Х + 2 Ц ) U g rad +Х U grad /^ , а для отыскания fi'_{dt is} используется выражение (31). При известных теперь константах далее найдем радиальные перемещения и радиальные напряжения Коши, моментные и полные напряжения.

• 5.    Результаты расчетов

Рассмотрим результаты вычисления распределения по координате £ безразмерных температуры, перемещений, деформаций, напряжений Коши, моментных и полных напряжений в цилиндре с теплозащитным покрытием. Во всех расчетах принято: a = 0,6 ; R ₀ = 0,9 ; Р ₀ = 0,4 ; Х 1 = Ц 1 = Y 1 = к 1 = 1.

На примере однородного покрытия проведена численная верификация предложенной схемы решения. При этом в расчетах полагалось, что термомеханические характеристики материала покрытия следующие: Х ₂ = 2; ц ₂ = 1,5; Y 2 = 1; к ₂ = 0,1. Аналитические выражения для перемещений в случае однородного покрытия, согласно [15], представлялись в виде:

U ⁽¹⁾( ^ ) = G£ + G- +

v. I m Г ЕЛ Г ЕЛ

⁷* . 0 0 J П W ^{( 1 )} ( П ) d П + G з 1 1 1 I + G 4 K 1 1 - I ,

( Х 1 + 2 Ц 1 ) ^ a             Ы Ы

U ⁽²⁾( ^ ) = G₅ ^+ G- +

.     0 0 J n W ⁽²⁾ ( n ) d n + G 7 1 1 ^f ^1 + G 8 K 1 f ^1 ,

I X 2 + 2 ^ 2 ) ^ R 0                       V^a/        \^aJ

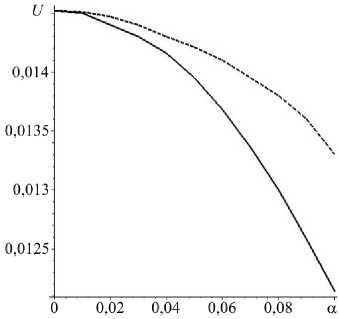
Рис. 1. Зависимость радиального перемещения на внутренней границе цилиндра от градиентного параметра a ; точное (сплошная линия) и приближенное (штриховая линия) решения

где 1 1 ( ^/a ) , K 1 ( ^/a ) — модифицированные функции Бесселя 1-го и 2-го рода первого порядка. В формуле (37) константы интегрирования G ₁, ..., G ₈ определялись путем удовлетворения граничных условий (25)–(27).

На рисунке 1 приведены графики, отражающие зависимость радиального перемещения на внутренней границе цилиндра от параметра 0 < a <  0,1. При этом для сравнения изображены точное решение, найденное по формулам (37), и приближенное решение с использованием метода пристрелки и асимптотической формулы (36). Максимальное отличие вычисленного перемещения от точного составило 10% при a = 0,1. При меньших значениях a решения ближе друг к другу: так, при a = 0,01 они отличаются на 0,07%. Выяснено, что предложенная численная схема решения задачи при a< 0,03 дает погрешность перемещений и напряжений, не превосходящую 1%.

Далее показано распределение температуры (Рис. 2а) и перемещения (Рис. 2б). Для сравнения приведены решения задачи для перемещения в классической постановке при a = 0 и в градиентной постановке при a = 0,03.

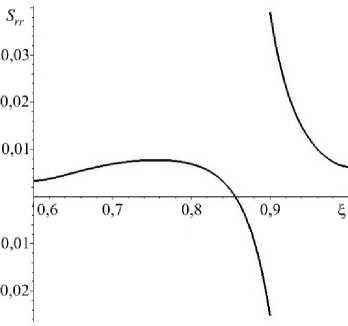
Рисунок 3 содержит распределение радиального напряжения Коши Srr (Рис. 3а) и моментного напряжения Mrrr (Рис. 3б) при значении масштабного параметра a = 0,03. На рисунке 3а видно, что радиальные напряжения Коши на границе сопряжения терпят разрыв, что связано как с разностью термомеханических характеристик цилиндра и покрытия, так и с непрерывностью перемещений и их производных на границе раздела разнородных материалов. Из рисунка 3б следует, что моментные

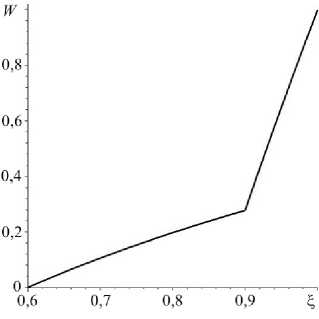
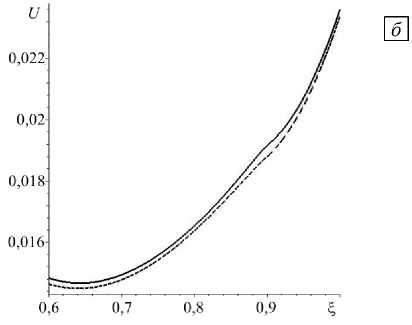
Рис. 2. Распределение по радиальной координате ^ температуры ( а ) и перемещения ( б ); точное решение при a = 0 (сплошная линия) и решение в градиентной постановке при a = 0,03 (штриховая линия)

а

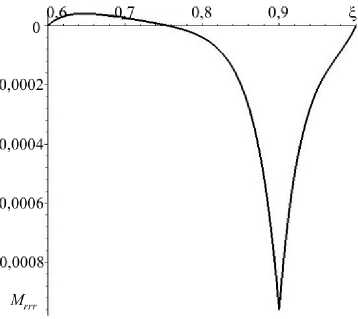
Рис. 3. Распределение по радиальной координате Е радиального напряжения Коши ( а ) и моментного напряжения М_т ( б ) при а = 0,03

напряжения M_rrr при малых значениях градиентного параметра в десятки раз меньше напряжений Коши. Они принимают пиковое значение на поверхности сопряжения.

На рисунке 4 приведено распределение полных напряжений: радиального (Рис. 4 а ) и окружного (Рис. 4 б ), в зависимости от радиальной координаты. При этом сплошной линией изображено решение задачи на основе классической постановки, штриховой линией — решение задачи в градиентной постановке при а = 0,03 . По рисункам 2, 4 можно заключить, что с увеличением масштабного параметра уменьшаются значения перемещения и полных окружных напряжений, а полные радиальные напряжения терпят разрыв.

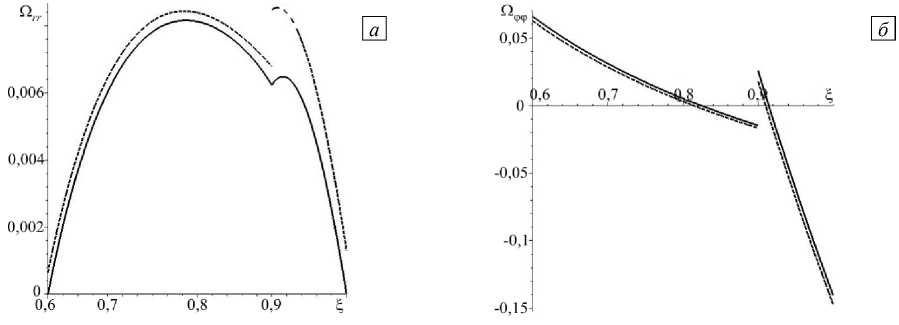
Рис. 4. Распределение по радиальной координате Е полных напряжений: радиального напряжения ( а ) и окружного напряжения ( б ); точное решение при а = 0 (сплошная линия) и приближенное решение при а = 0,03 (штриховая линия)

Во второй серии расчетов полагалось, что покрытие цилиндра изготовлено из неоднородного материала с законом неоднородности, обеспечивающим непрерывное изменение термомеханических характеристик при переходе через поверхность сопряжения в виде: Х ₂ ( Е ) = 1 + ( 10 ^- 9 ) N , ц ₂ ( Е ) = 1 + 0,5 ( 10 ^- 9 ) N , Y 2 ( Е ) = 1, к 2 ( Е ) = 1 - 0,9 ( 10 ^- 9 ) N , N = 1,2,... .

Покажем результаты вычисления перемещений, деформаций и напряжений при показателе неоднородности N = 1. На рисунке 5 показаны радиальные распределения перемещений (Рис. 5 а ) и полного окружного напряжения (Рис. 5 б ). Из рисунка следует, что при неоднородном покрытии, в отличие от случая однородного покрытия, полные окружные напряжения не претерпевают разрыва, а изменяются непрерывно, при этом увеличение градиентного параметра так же, как и при однородном покрытии, приводит к уменьшению перемещений и окружных напряжений.

На рисунке 6 представлено радиальное распределение деформаций dU/d Е в системе «цилиндр-покрытие» при однородном и неоднородном ( N = 1) покрытии. Из рисунка видно, что при а = 0 в случае однородного покрытия деформации терпят разрыв, а при неоднородном покрытии они непрерывны. В градиентной постановке деформации непрерывны при обоих видах покрытия.

Также проведено исследование влияния различных законов неоднородности, характеризующихся параметром N , на распределение перемещений и напряжений. На рисунке 7 показаны графики радиального распределения перемещений и полных радиальных напряжений при а = 0,03 и различных значениях параметра N . Из рисунка следует, что закон неоднородности оказывает сильное влияние на распределение перемещений и напряжений.

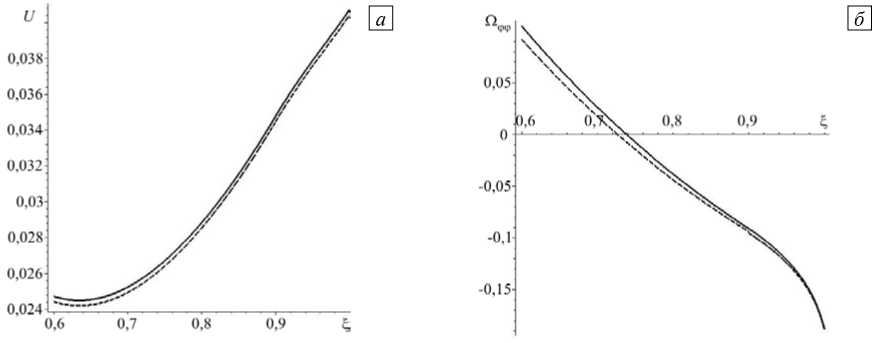
Рис. 5. Распределение по радиальной координате 5 перемещения ( а ) и полного окружного напряжения ( б ); точное решение при а = 0 (сплошная линия) и приближенное решение а = 0,03 (штриховая линия)

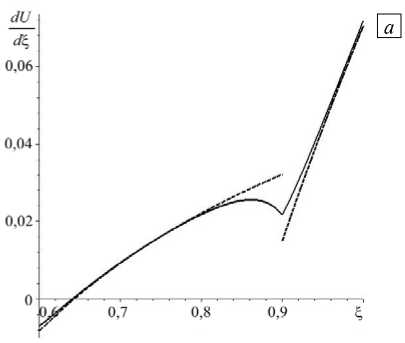
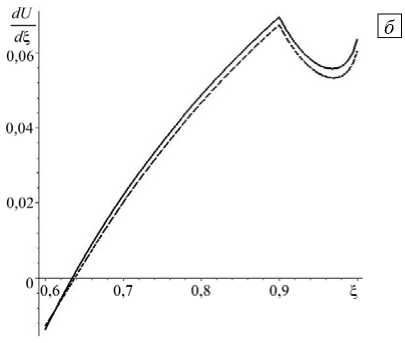
Рис. 6. Распределение по радиальной координате 5 деформаций dU/d 5 в случаях однородного ( а ) и неоднородного ( б ) покрытия; точное решение при а = 0 (сплошная линия) и приближенное решение при а = 0,03 (штриховая линия)

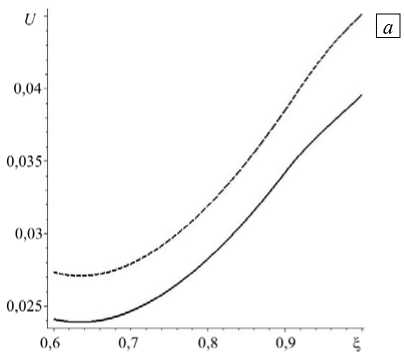
Рис. 7. Распределение по радиальной координате 5 перемещения ( а ) и полного радиального напряжения ( б ) при а = 0,03 и разных значениях параметра неоднородности N : 1 (сплошная линия) и 2 (штриховая линия)

б

• 6.    Выводы

Исследована задача градиентной термоупругости для цилиндра, имеющего термозащитное покрытие. Перемещения и напряжения представлены в виде суммы решений классической термоупругой задачи и градиентных слагаемых. Задача термоупругости в классической постановке решается методом пристрелки. Градиентные слагаемые получаются при помощи асимптотического метода ВКБ. Показано отличие друг от друга распределений перемещений и напряжений по радиальной координате, рассчитанных по классической теории и найденных с использованием градиентной теории термоупругости. Выяснено, что увеличение значения градиентного параметра снижает значения радиальных перемещений и полных напряжений. Моментные напряжения при малых значениях градиентного параметра намного меньше полных напряжений. Скачок напряжений Коши в окрестности поверхности сопряжения разнородных материалов объясняется непрерывностью перемещений и их градиентов. Исследовано влияние параметра неоднородности в степенном законе, моделирующем термомеханические характеристики неоднородного покрытия, на распределения по радиальной координате перемещений и полных напряжений.

Учет влияния градиентного параметра при анализе НДС полого цилиндра с покрытием имеет большое практическое значение при расчете на прочность и оценке потери устойчивости термозащитного покрытия. Разработанный подход может быть применен при нахождении приближенного аналитического решения задачи градиентной термоупругости для конечного цилиндра.