Решение задачи инвестирования инновационных проектов с помощью метода динамического программирования

Кривошапова Г.А.; Яркина А.А.; Иценко М.Ю.; Krivoshapova G.A.; Yarkina A.A.; Itsenko M.Y.

Решение задачи инвестирования инновационных проектов с помощью метода динамического программирования

Автор: Кривошапова Г.А., Яркина А.А., Иценко М.Ю.

Журнал: Теория и практика современной науки @modern-j

Рубрика: Математика, информатика и инженерия

Статья в выпуске: 1 (55), 2020 года.

Бесплатный доступ

В статье рассматриваются решение задачи инвестирования инновационных проектов. Для решения выбран метод динамического программирования. Поиск решения был проведен с помощью онлайн-калькулятора.

Оптимальное распределение, динамическое программирование, стратегия

Короткий адрес: https://sciup.org/140275024

IDR: 140275024 | УДК: 004.94

Solution of problem of investments in innovative projects with the use of dynamic programming

The article describes the solution of problem of investment in innovative projects. For the solving the task, the dynamic programming method was used. The solution search was made with the use of online - calculator.

Текст научной статьи Решение задачи инвестирования инновационных проектов с помощью метода динамического программирования

Пусть имеются пять инвестиционных проектов, между которыми распределяется 300 тыс. ден. ед. Денежные средс тв а распределяются суммами кратными 50 тыс. ден. ед. Значения g i ( x ⁾⁽ i = ^1,5) ожидаемой прибыли от реализации каждого из инвестиционных проектов в зависимости от выделенной суммы х приведены в таблице 1. Составить план распределения средств, максимизирующий общий прирост прибыли.

Для решения задачи был выбран онлайн-калькулятор «Задача оптимального распределения инвестиций» [1].

На рисунке 1 представлены исходные данные.

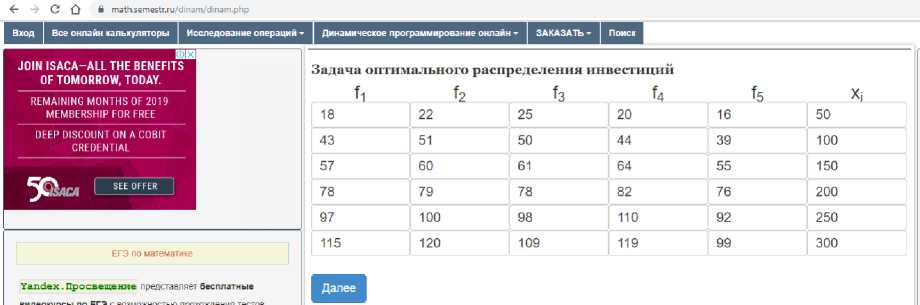
Рисунок 1 - Исходные данные

Представим поэтапное решение задачи оптимального распределения инвестиций.

На каждом k-ом шаге оптимизируется инвестирование не всех проектов сразу, а только проекты с k-ого по 5-ый. При этом, будем считать, что в остальные проекты (с 1-ого по (k-1)-ое) тоже вкладываются некоторые средства, и потому на инвестирование проектов с k-ого по 5-ый остаются не все средства, а некоторая сумма сk≤300 тыс.ден.ед. Эта величина и будет являться переменной состояния системы. Переменной управления на k-ом шаге назовем величину хk средств, вкладываемых в k-ый проект. В качестве функционального уравнения Беллмана fk(сk) на к-ом шаге в этой задаче можно выбрать максимально возможную прибыль, которую можно получить по проектам с k-ого по 5-ый при условии, что на их инвестирование осталось ск средств.

I этап. Условная оптимизация.

1-ый шаг. k = 5.

Предположим, что все средства в количестве х5 = 300 отданы проекту №5. В этом случае, максимальный доход, как это видно из таблицы, составит f5(u5) = 99, следовательно, F5(e5) = f5(u5).

Таблица 1

e4	u5	e5 = e4 - u5	f5(u5)	F*5(e5)	u5(e5)
50	0	50	0
50	50	0	16	16	50
100	0	100	0
	50	50	16
	100	0	39	39	100
150	0	150	0
	50	100	16
	100	50	39
	150	0	55	55	150
200	0	200	0
	50	150	16
	100	100	39
	150	50	55
	200	0	76	76	200
250	0	250	0
	50	200	16
	100	150	39
	150	100	55
	200	50	76
	250	0	92	92	250
300	0	300	0
	50	250	16
	100	200	39
	150	150	55
	200	100	76

	250	50	92
	300	0	99	99	300

2-ый шаг. k = 4.

Определяем оптимальную стратегию при распределении денежных средств между проектами №4, 5. При этом рекуррентное соотношение

Беллмана имеет вид: F4(e4) = max(x4 ≤ e4)(f4(u4) + F5(e4-u4)).

Таблица 2

e3	u4	e4 = e3 - u4	f4(u4)	F*4(e3)	F3(u4,e3)	F*4(e4)	u4(e4)
50	0	50	0	16	16
50	50	0	20	0	20	20	50
100	0	100	0	39	39
	50	50	20	16	36
	100	0	44	0	44	44	100
150	0	150	0	55	55
	50	100	20	39	59
	100	50	44	16	60
	150	0	64	0	64	64	150
200	0	200	0	76	76
	50	150	20	55	75
	100	100	44	39	83	83	100
	150	50	64	16	80
	200	0	82	0	82
250	0	250	0	92	92
	50	200	20	76	96
	100	150	44	55	99
	150	100	64	39	103
	200	50	82	16	98
	250	0	110	0	110	110	250

300	0	300	0	99	99
	50	250	20	92	112
	100	200	44	76	120
	150	150	64	55	119
	200	100	82	39	121
	250	50	110	16	126	126	250
	300	0	119	0	119

3-ый шаг. k = 3.

Определяем оптимальную стратегию при распределении денежных средств между проектами №3, 4, 5. При этом рекуррентное соотношение

Беллмана имеет вид: F3(e3) = max(x3 ≤ e3)(f3(u3) + F4(e3-u3))

Таблица 3

e2	u3	e3 = e2 - u3	f3(u3)	F*3(e2)	F2(u3,e2)	F*3(e3)	u3(e3)
50	0	50	0	20	20
50	50	0	25	0	25	25	50
100	0	100	0	44	44
	50	50	25	20	45
	100	0	50	0	50	50	100
150	0	150	0	64	64
	50	100	25	44	69
	100	50	50	20	70	70	100
	150	0	61	0	61
200	0	200	0	83	83
	50	150	25	64	89
	100	100	50	44	94	94	100
	150	50	61	20	81
	200	0	78	0	78
250	0	250	0	110	110

	50	200	25	83	108
	100	150	50	64	114	114	100
	150	100	61	44	105
	200	50	78	20	98
	250	0	98	0	98
300	0	300	0	126	126
	50	250	25	110	135	135	50
	100	200	50	83	133
	150	150	61	64	125
	200	100	78	44	122
	250	50	98	20	118
	300	0	109	0	109

4-ый шаг. k = 2.

Определяем оптимальную стратегию при распределении денежных средств между проектами №2, 3, 4, 5. При этом рекуррентное соотношение

Беллмана имеет вид: F2(e2) = max(x2 ≤ e2)(f2(u2) + F3(e2-u2))

Таблица 4

e1	u2	e2 = e1 - u2	f2(u2)	F*2(e1)	F1(u2,e1)	F*2(e2)	u2(e2)
50	0	50	0	25	25	25	0
50	50	0	22	0	22
100	0	100	0	50	50
	50	50	22	25	47
	100	0	51	0	51	51	100
150	0	150	0	70	70
	50	100	22	50	72
	100	50	51	25	76	76	100
	150	0	60	0	60
200	0	200	0	94	94

	50	150	22	70	92
	100	100	51	50	101	101	100
	150	50	60	25	85
	200	0	79	0	79
250	0	250	0	114	114
	50	200	22	94	116
	100	150	51	70	121	121	100
	150	100	60	50	110
	200	50	79	25	104
	250	0	100	0	100
300	0	300	0	135	135
	50	250	22	114	136
	100	200	51	94	145	145	100
	150	150	60	70	130
	200	100	79	50	129
	250	50	100	25	125
	300	0	120	0	120

5-ый шаг. k = 1.

Определяем оптимальную стратегию при распределении денежных средств между проектами №1, 2, 3, 4, 5. При этом рекуррентное соотношение

Беллмана имеет вид: F1(e1) = max(x1 ≤ e1)(f1(u1) + F2(e1-u1))

Таблица 5

e0	u1	e1 = e0 - u1	f1(u1)	F*1(e0)	F0(u1,e0)	F*1(e1)	u1(e1)
50	0	50	0	25	25	25	0
50	50	0	18	0	18
100	0	100	0	51	51	51	0
	50	50	18	25	43
	100	0	43	0	43

150	0	150	0	76	76	76	0
	50	100	18	51	69
	100	50	43	25	68
	150	0	57	0	57
200	0	200	0	101	101	101	0
	50	150	18	76	94
	100	100	43	51	94
	150	50	57	25	82
	200	0	78	0	78
250	0	250	0	121	121	121	0
	50	200	18	101	119
	100	150	43	76	119
	150	100	57	51	108
	200	50	78	25	103
	250	0	97	0	97
300	0	300	0	145	145	145	0
	50	250	18	121	139
	100	200	43	101	144
	150	150	57	76	133
	200	100	78	51	129
	250	50	97	25	122
	300	0	115	0	115

Рассмотрим построение таблиц и последовательность проведения расчетов.

Столбцы 1 (вложенные средства), 2 (проект) и 3 (остаток средств) для всех трех таблиц одинаковы, поэтому их можно было бы сделать общими. Столбец 4 заполняется на основе исходных данных о функциях дохода, значения в столбце 5 берутся из столбца 7 предыдущей таблицы, столбец 6 заполняется суммой значений столбцов 4 и 5 (в таблице 5-го шага столбцы 5

и 6 отсутствуют).

В столбце 7 записывается максимальное значение предыдущего столбца для фиксированного начального состояния, и в 8 столбце записывается управление из 2 столбца, на котором достигается максимум в 7.

Этап II. Безусловная оптимизация.

Из таблицы 5-го шага имеем F*1(e0 = 300) = 145. То есть максимальный доход всей системы при количестве средств e0 = 300 равен 145

Из этой же таблицы получаем, что 1-му проекту следует выделить u*1(e0 = 300) = 0

При этом остаток средств составит:

e1 = e0 - u1 = 300 - 0 = 300

Из таблицы 4-го шага имеем F*2(e1 = 300) = 145. То есть максимальный доход всей системы при количестве средств e1 = 300 равен 145

Из этой же таблицы получаем, что 2-му проекту следует выделить u*2(e1 = 300) = 100

При этом остаток средств составит:

e2 = e1 - u2 = 300 - 100 = 200

Из таблицы 3-го шага имеем F*3(e2 = 200) = 94. То есть максимальный доход всей системы при количестве средств e2 = 200 равен 94

Из этой же таблицы получаем, что 3-му проекту следует выделить u*3(e2 = 200) = 100

При этом остаток средств составит:

e3 = e2 - u3 = 200 - 100 = 100

Из таблицы 2-го шага имеем F*4(e3 = 100) = 44. То есть максимальный доход всей системы при количестве средств e3 = 100 равен 44

Из этой же таблицы получаем, что 4-му проекту следует выделить u*4(e3 = 100) = 100

При этом остаток средств составит:

e4 = e3 - u4 = 100 - 100 = 0

Последнему проекту достается 0

Итак, инвестиции в размере 300 необходимо распределить следующим образом:

1-му проекту выделить 0

2-му проекту выделить 100

3-му проекту выделить 100

4-му проекту выделить 100

5-му проекту выделить 0

Что обеспечит максимальный доход, равный 145

Список литературы Решение задачи инвестирования инновационных проектов с помощью метода динамического программирования

Онлайн-калькулятор / Уровень доступа https://math.semestr.ru/dinam/dinam.php

300	0	300	0	99	99
	50	250	20	92	112
	100	200	44	76	120
	150	150	64	55	119
	200	100	82	39	121
	250	50	110	16	126	126	250
	300	0	119	0	119

	50	200	25	83	108
	100	150	50	64	114	114	100
	150	100	61	44	105
	200	50	78	20	98
	250	0	98	0	98
300	0	300	0	126	126
	50	250	25	110	135	135	50
	100	200	50	83	133
	150	150	61	64	125
	200	100	78	44	122
	250	50	98	20	118
	300	0	109	0	109

	50	150	22	70	92
	100	100	51	50	101	101	100
	150	50	60	25	85
	200	0	79	0	79
250	0	250	0	114	114
	50	200	22	94	116
	100	150	51	70	121	121	100
	150	100	60	50	110
	200	50	79	25	104
	250	0	100	0	100
300	0	300	0	135	135
	50	250	22	114	136
	100	200	51	94	145	145	100
	150	150	60	70	130
	200	100	79	50	129
	250	50	100	25	125
	300	0	120	0	120

150	0	150	0	76	76	76	0
	50	100	18	51	69
	100	50	43	25	68
	150	0	57	0	57
200	0	200	0	101	101	101	0
	50	150	18	76	94
	100	100	43	51	94
	150	50	57	25	82
	200	0	78	0	78
250	0	250	0	121	121	121	0
	50	200	18	101	119
	100	150	43	76	119
	150	100	57	51	108
	200	50	78	25	103
	250	0	97	0	97
300	0	300	0	145	145	145	0
	50	250	18	121	139
	100	200	43	101	144
	150	150	57	76	133
	200	100	78	51	129
	250	50	97	25	122
	300	0	115	0	115

300	0	300	0	99	99
	50	250	20	92	112
	100	200	44	76	120
	150	150	64	55	119
	200	100	82	39	121
	250	50	110	16	126	126	250
	300	0	119	0	119

	50	200	25	83	108
	100	150	50	64	114	114	100
	150	100	61	44	105
	200	50	78	20	98
	250	0	98	0	98
300	0	300	0	126	126
	50	250	25	110	135	135	50
	100	200	50	83	133
	150	150	61	64	125
	200	100	78	44	122
	250	50	98	20	118
	300	0	109	0	109

	50	150	22	70	92
	100	100	51	50	101	101	100
	150	50	60	25	85
	200	0	79	0	79
250	0	250	0	114	114
	50	200	22	94	116
	100	150	51	70	121	121	100
	150	100	60	50	110
	200	50	79	25	104
	250	0	100	0	100
300	0	300	0	135	135
	50	250	22	114	136
	100	200	51	94	145	145	100
	150	150	60	70	130
	200	100	79	50	129
	250	50	100	25	125
	300	0	120	0	120

150	0	150	0	76	76	76	0
	50	100	18	51	69
	100	50	43	25	68
	150	0	57	0	57
200	0	200	0	101	101	101	0
	50	150	18	76	94
	100	100	43	51	94
	150	50	57	25	82
	200	0	78	0	78
250	0	250	0	121	121	121	0
	50	200	18	101	119
	100	150	43	76	119
	150	100	57	51	108
	200	50	78	25	103
	250	0	97	0	97
300	0	300	0	145	145	145	0
	50	250	18	121	139
	100	200	43	101	144
	150	150	57	76	133
	200	100	78	51	129
	250	50	97	25	122
	300	0	115	0	115

300	0	300	0	99	99
	50	250	20	92	112
	100	200	44	76	120
	150	150	64	55	119
	200	100	82	39	121
	250	50	110	16	126	126	250
	300	0	119	0	119

	50	200	25	83	108
	100	150	50	64	114	114	100
	150	100	61	44	105
	200	50	78	20	98
	250	0	98	0	98
300	0	300	0	126	126
	50	250	25	110	135	135	50
	100	200	50	83	133
	150	150	61	64	125
	200	100	78	44	122
	250	50	98	20	118
	300	0	109	0	109

	50	150	22	70	92
	100	100	51	50	101	101	100
	150	50	60	25	85
	200	0	79	0	79
250	0	250	0	114	114
	50	200	22	94	116
	100	150	51	70	121	121	100
	150	100	60	50	110
	200	50	79	25	104
	250	0	100	0	100
300	0	300	0	135	135
	50	250	22	114	136
	100	200	51	94	145	145	100
	150	150	60	70	130
	200	100	79	50	129
	250	50	100	25	125
	300	0	120	0	120

150	0	150	0	76	76	76	0
	50	100	18	51	69
	100	50	43	25	68
	150	0	57	0	57
200	0	200	0	101	101	101	0
	50	150	18	76	94
	100	100	43	51	94
	150	50	57	25	82
	200	0	78	0	78
250	0	250	0	121	121	121	0
	50	200	18	101	119
	100	150	43	76	119
	150	100	57	51	108
	200	50	78	25	103
	250	0	97	0	97
300	0	300	0	145	145	145	0
	50	250	18	121	139
	100	200	43	101	144
	150	150	57	76	133
	200	100	78	51	129
	250	50	97	25	122
	300	0	115	0	115