Решение задачи коммивояжера при помощи генетического алгоритма

Annotation:

The article is devoted to solving the traveling salesman problem. It discusses in detail all stages of the solution.

Keyword: genetic algorithm, problem, solution, algorithm.

1 ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Задачи коммивояжера решаются посредством различных методов, выведенных в результате теоретических исследований. Все эффективные методы (сокращающие полный перебор) — методы эвристические. В большинстве эвристических методов находится не самый эффективный маршрут, а приближённое решение. Зачастую востребованы алгоритмы, постепенно улучшающие некоторое текущее приближенное решение. Выделяют следующие группы методов решения задач коммивояжера, которые относят к простейшим:

Полный перебор.

Полный перебор (или метод «грубой силы») — метод решения задачи путем перебора всех возможных вариантов. Сложность полного перебора зависит от количества всех возможных решений задачи. Если пространство решений очень велико, то полный перебор может не дать результатов в течение нескольких лет или даже столетий.

Случайный перебор.

Обычно выбор решения можно представить последовательностью выборов. Если делать эти выборы с помощью какого-либо случайного механизма, то решение находится очень быстро, так что можно находить решение многократно и запоминать «рекорд», т. е. наилучшее из встретившихся решений. Этот наивный подход существенно улучшается, когда удается учесть в случайном механизме перспективность тех или иных выборов, т. е. комбинировать случайный поиск с эвристическим методом и методом локального поиска. Такие методы применяются, например, при составлении расписаний для Аэрофлота.

Жадные алгоритмы (метод ближайшего соседа, метод включения ближайшего города, метод самого дешевого включения).

Жадный алгоритм – алгоритм нахождения наикратчайшего расстояния путём выбора самого короткого, ещё не выбранного ребра, при условии, что оно не образует цикла с уже выбранными рёбрами. «Жадным» этот алгоритм назван потому, что на последних шагах приходится жестоко расплачиваться за жадность. При решении задачи коммивояжера жадный алгоритм превратится в стратегию «иди в ближайший (в который еще не входил) город».

Метод минимального основного дерева (деревянный алгоритм);

В основе алгоритма лежит утверждение: «Если справедливо неравенство треугольника, то для каждой цепи верно, что расстояние от начала до конца цепи меньше (или равно) суммарной длины всех ребер цепи». Это обобщение расхожего убеждения, что прямая короче кривой. Деревянный алгоритм для решения задачи коммивояжера будет следующим: строится на входной сети задачи коммивояжера кратчайшее основное дерево и удваиваются все его ребра. В результате получаем граф — связный с вершинами, имеющими только четные степени. Затем строится эйлеров цикл, начиная с вершины 1, цикл задается перечнем вершин. Просматривается перечень вершин, начиная с 1, и зачеркивается каждая вершина, которая повторяет уже встреченную в последовательности. Останется тур, который и является результатом алгоритма.

Метод имитации отжига.

Экзотическое название данного алгоритма связано с методами имитационного моделирования в статистической физике, основанными на технике Монте-Карло. Исследование кристаллической решетки и поведения атомов при медленном остывании тела привело к появлению на свет вероятностных алгоритмов, которые оказались чрезвычайно эффективными в комбинаторной оптимизации. Впервые это было замечено в 1983 году. Сегодня этот алгоритм является популярным как среди практиков благодаря своей простоте, гибкости и эффективности, так и среди теоретиков, поскольку для данного алгоритма удается аналитически исследовать его свойства и доказать асимптотическую сходимость. Алгоритм имитации отжига относится к классу пороговых алгоритмов локального поиска. На каждом шаге этого алгоритма для текущего решения ik в его окрестности N(ik) выбирается некоторое решение j и, если разность по целевой функции между новым и текущим решением не превосходит заданного порога tk, то новое решение j заменяет текущее. В противном случае выбирается новое соседнее решение. На практике применяются различные модификации более эффективных методов.

Метод ветвей и границ;

Метод ветвей и границ предложен в 1963 году группой авторов Дж. Литлом, К. Мурти, Д. Суини, К. Кэролом. Широко используемый вариант поиска с возвращением, фактически является лишь специальным частным случаем метода 3

поиска с ограничениями. Ограничения в данном случае основываются на предположении, что на множестве возможных и частичных решений задана некоторая функция цены и что нужно найти оптимальное решение, т.е. решение с наименьшей ценой. Для применения метода ветвей и границ функция цены должна обладать тем свойством, что цена любого частичного решения не превышает цены любого расширения этого частичного решения (Заметим, что в большинстве случаев функция цены неотрицательна и даже удовлетворяет более сильному требованию). Столь большой успех применения данного метода объясняется тем, что авторы первыми обратили внимание на широту возможностей метода, отметили важность использования специфики задачи и сами воспользовались спецификой задачи коммивояжера.

В основе метода ветвей и границ лежит идея последовательного разбиения множества допустимых решений на подмножества. На каждом шаге метода элементы разбиения подвергаются проверке для выяснения, содержит данное подмножество оптимальное решение или нет. Проверка осуществляется посредством вычисления оценки снизу для целевой функции на данном подмножестве. Если оценка снизу не меньше рекорда — наилучшего из найденных решений, то подмножество может быть отброшено. Проверяемое подмножество может быть отброшено еще и в том случае, когда в нем удается найти наилучшее решение. Если значение целевой функции на найденном решении меньше рекорда, то происходит смена рекорда. По окончанию работы алгоритма рекорд является результатом его работы. Если удается отбросить все элементы разбиения, то рекорд — оптимальное решение задачи. В противном случае, из неотброшенных подмножеств выбирается наиболее перспективное (например, с наименьшим значением нижней оценки), и оно подвергается разбиению. Новые подмножества вновь подвергаются проверке и т. д.

• 2 МЕТОД ВЕТВЕЙ И ГРАНИЦ

Для решения задачи коммивояжера методом ветвей и границ необходимо выполнить следующую последовательность действий:

• а)    Построение матрицы с исходными данными.

• б)    Нахождение минимума по строкам.

• в)    Редукция строк.

• г)    Нахождение минимума по столбцам.

• д)    Редукция столбцов.

• е)    Вычисление оценок нулевых клеток.

• ж)    Редукция матрицы.

• и)    Если полный путь еще не найден, переходим к пункту б, если найден к пункту и.

• к)    Вычисление итоговой длины пути и построение маршрута.

Подробная методика решения.

Сначала необходимо длины дорог соединяющих города представить в соответствии с рисунком 1.

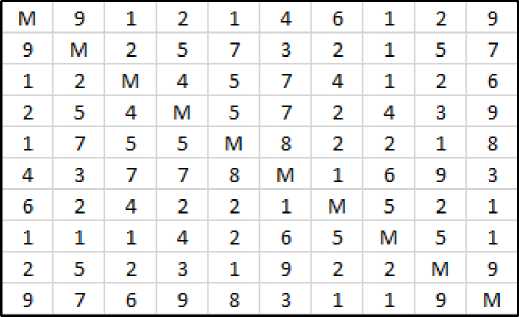
Рисунок 1 – Исходные данные

В нашем примере у нас 10 городов и в таблице указано расстояние от каждого города к 9-м другим, в зависимости от направления движения.

Расстояние от города к этому же городу обозначено буквой М. Также используется знак бесконечности. Это сделано для того, чтобы данный отрезок путь был условно принят за бесконечно длинный. Тогда не будет смысла выбрать движение от 1-ого города к 1-му, от 2-ого ко 2-му, и т. п. в качестве отрезка маршрута.

Находим минимальное значение в каждой строке (di) и выписываем его в отдельный столбец, в соответствие с рисунком 2.

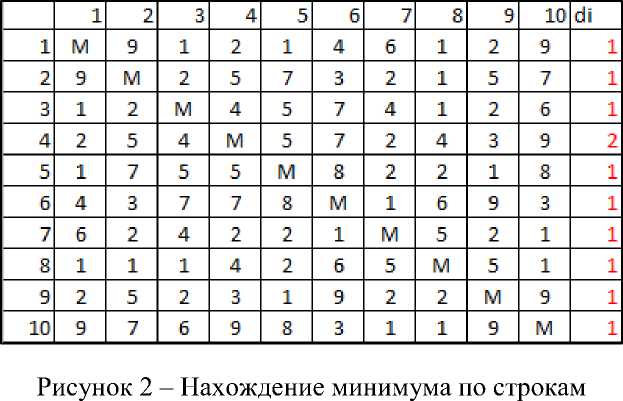
Производим редукцию строк – из каждого элемента в строке вычитаем соответствующее значение найденного минимума (di), в соответствие с рисунком 3.

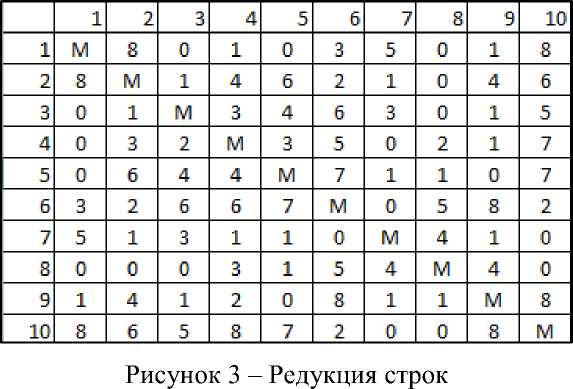
В итоге в каждой строке будет хотя бы одна нулевая клетка. Далее находим минимальные значения в каждом столбце (dj). Эти минимумы выписываем в отдельную строку, в соответствие с рисунком 4.

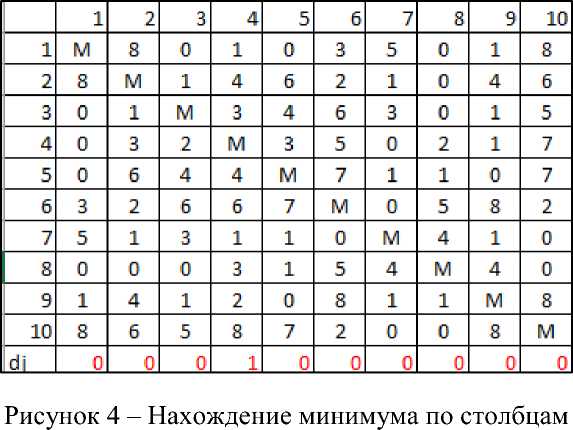
Вычитаем из каждого элемента матрицы соответствующее ему dj, в соответствии с рисунком 5.

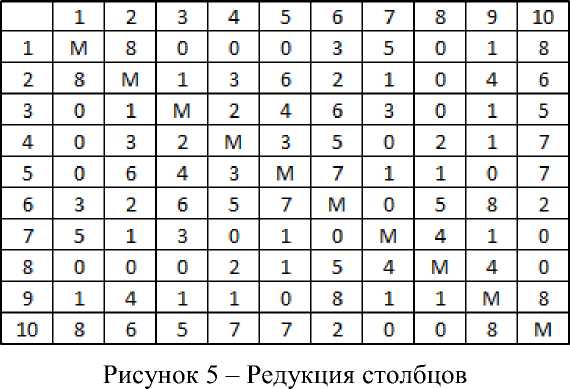
Для каждой нулевой клетки получившейся преобразованной матрицы находим «оценку». Ею будет сумма минимального элемента по строке и минимального элемента по столбцу, в которых размещена данная нулевая клетка. Сама она при этом не учитывается. Найденные ранее di и dj не учитываются. Полученную оценку записываем рядом с нулем, в скобках, в соответствие с рисунком 6.

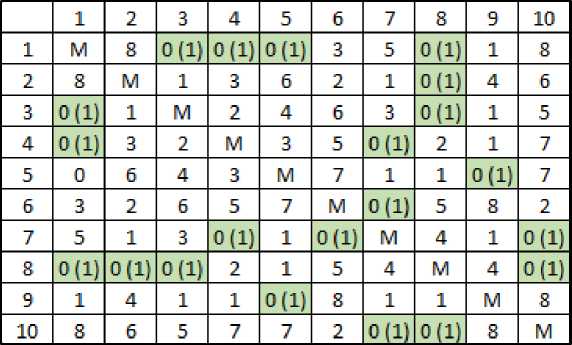
Рисунок 6 – Вычисление оценок нулевых клеток

Выбираем нулевую клетку с наибольшей оценкой. Заменяем ее на «М». Мы нашли один из отрезков пути. Выделяем его в соответствие с рисунком 7.

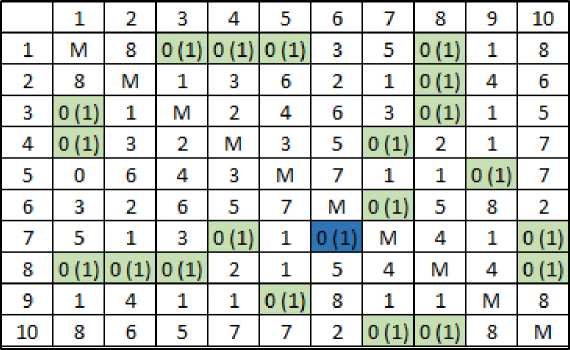
Рисунок 7 – Выделение клетки пути

Ту строку и тот столбец, где образовалось две «М» полностью вычеркиваем. В клетку, соответствующую обратному пути, ставим еще одну букву «М» (т. к. мы уже не будем возвращаться обратно), в соответствии с рисунком 8.

	1	2	3	4	5	6	7	8	9	10
1	М	8	0(1]	0(1]	o(ij	3	5	0(1)	1	8
2	В	М	1	3	6	2	1	0(1)	4	6
3	0(1)	1	м	2	4	6	3	0(1)	1	5
4	0(1}	3	2	М	3	5	0(1}	2	1	7
5	0	6	4	3	М	7	1	1	0(1)	7
6	3	2	6	5	7	М	0(1)	5	8	2
7	5	1	3	0(1]	1	0(1}	м	4	1	0(1]
8	0(1}	0(1}	0(1}	2	1	5	4	М	4	0(1)
9	1	4	1	1	0(1]	8	1	1	М	8
10	8	6	5	7	7	2	0(1)	0(1)	8	М

Рисунок 8 – Редукция матрицы

Если полный путь еще не найден, переходим к пункту Б, если найден к пункту И. Если мы еще не нашли все отрезки пути, то возвращаемся к пункту Б и вновь ищем минимумы по строкам и столбцам, проводим их редукцию, считаем оценки нулевых клеток и т. д. Если все отрезки пути найдены (или найдены еще не все отрезков, но оставшаяся часть пути очевидна) – переходим к пункту И.

Найдя все отрезки пути, остается только соединить их между собой и рассчитать общую длину пути (стоимость поездки по этому маршруту, затраченное время и т. д.). Длины дорог, соединяющих города, берем из самой первой таблицы с исходными данными.

В нашем примере маршрут получился следующий: 6 → 7 → 4 → 1 → 5 → 9 → 3 → 10 → 8 → 2 → 6.

Общая длина пути: L = 20.

3 ПРОГРАММНАЯ РЕАЛИЗАЦИЯ

Для более удобного решения можно на основе данного алгоритма написать программу. Она будет реализована на языке программирования Java. Программа так же будет, кроме итогов решения, выводить шаги решения. Пример шага показан на рисунке 9.

STAGE 4	H:
di: [1	1, 1, 2, 1, 1, 1, 1, 1, l]j
dj: [0. Matrix	0, 0, 1, 0, 0, 0, 0, 0, 0]; after diff:
[M, 8,	0, 0, 0, 3, 5, 0, 1, 8]
[8, M,	1, 3, 6, 2, 1, 0, 4, 6]
[0, 1,	M, 2, 4, 6, 3, 0, 1, 5]
[0, 3,	2, M, 3, 5, 0, 2, 1, 7]
[0, 6,	4, 3, M, 7, 1, 1, 0, 7]
[3, 2,	6, 5, 7, M, 0, 5, 8, 2]
[5, 1,	3, 0, 1, 0, M, 4, 1, 0]
[0, 0,	0, 2, 1, 5, 4, M, 4, 0]
[1. 4,	1, 1, 0, 8, 1, 1, M, 8]
[8, 6, 5, 7, 7, 2, 0, 0, 8, M] Reduction matrix:
[M, 8,	0, 0, 0, 3, 0, 1, 8]
[8, M,	1, 3, 6, 2, 0, 4, 6]
[0, 1,	M, 2, 4, 6, 0, 1, 5]
[0, 3,	2, M, 3, 5, 2, 1, 7]
[0, 6,	4, 3, M, 7, 1, 0, 7]
[5, 1,	3, 0, 1, M, 4, 1, 0]
[0, 0,	0, 2, 1, 5, M, 4, 0]
[1. 4,	1, 1, 0, 8, 1, M, 8]
[8, 6, 5, 7, 7, 2, 0, 8, M] Path now: 6 -> 7

Рисунок 9 – Шаг 1 в программного коде

Основной метод решения задачи будет выглядеть в соответствие с рисунком 10.

void start(String path) { long start = System.currentTimeMiLLisQ;

Stack stack = new Stack<>();

int[][] matrix = readFile(path);

int[][] clone = clone(matrix);

List v = new ArrayList<>();

printMatrix(matrix);

int count = 1;

System. out . printin (" \n#############################^^           )

int[] di = getMinArray(matrix, false);

matrix = diffMatrix(matrix, di, false);

int[] dj = getMinArray(matrix, true);

matrix = diffMatrix(matrix, dj, true);

printMatrix(matrix);

matrix = getPath(matrix, stack, v);

}

printStack(stack);

}                                            '

printStack(stack);

Рисунок 10 – Основной метод решения задачи