Решение задачи конвективного теплообмена в винтовой системе координат

1.    Введение. Постановка задачи

Рассматривается неизотермическое течение жидкого металла в кольцевом канале с ребром, перпендикулярным стенкам и закрученным винтом против часовой стрелки (Рис. 1). Внутренняя труба

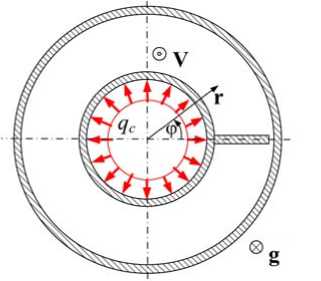
Рис. 1. Схема течения

нагревается с постоянной плотностью теплового потока, как по длине, так и по периметру сечения. Между ребром и внешней трубой имеется зазор.

В случае вертикального канала изучался теплообмен при подъемном течении жидкого металла, направленном навстречу вектору ускорения свободного падения g. Экспериментально исследования выполнялись на уникальном ртутном стенде кафедры инженерной теплофизики Национального исследовательского университета «МЭИ» (Москва). Также задача моделировалась численно. Полученные результаты представлены в работах [1] и [2]. Они послужили материалом для двух кандидатских диссертаций. Обе работы, несомненно, являются новыми в исследовании теплоносителей из рода жидких металлов. Но поскольку данные эксперимента и численного решения оказались неоднозначными, вопрос тождественности расчетной модели эксперименту остался неразрешенным.

Предлагаемая вниманию читателя работа содержит альтернативный вариант численного решения задачи теплообмена при течении в кольцевом канале с винтовым ребром в винтовой системе координат (ВСК) [3]. Несмотря на то, что винтовые течения в каналах нередко встречаются в технологическом и в энергетическом оборудовании [4, 5], модельные расчеты проводят, как правило, в декартовых координатах, в которых неудобно описывать геометрию криволинейных поверхностей. ВСК же дает очевидные преимущества: простоту геометрии расчетной области и удобство задания граничных условий. Используется структурированная расчетная сетка, элементы сетки не дробятся и совпадают с границами исследуемой области. Расчетная сетка может быть грубой и — по мере необходимости — сгущаться вблизи стенки. Применяется алгебраическая модель турбулентности, которая неплохо работает при моделировании течения жидкого металла в каналах. Все это увеличивает скорость расчета, а объем вычислений существенно уменьшает. Необходимо только записать систему уравнений и, при возможности, сформулировать допущения, упрощающие расчет.

Описание методики вывода уравнений в ВСК редко, но встречается в публикациях, например в [6]. Неоднозначность выбора базиса, громоздкость вычислений, сомнения в аккуратности математических выкладок ограничивают использование подобного подхода к решению задачи винтового течения. В данной работе, на взгляд автора, методика вывода уравнений наиболее ясная и понятная, удачно выбран базис и компактно записаны дополнительные слагаемые, которые необходимо добавить в уравнения, записанные в цилиндрической системе, чтобы перейти к ВСК. Представленная методика, в общем, позволяет вывести уравнения для любой криволинейной координатной системы. Пример расчета в ВСК и сравнение с аналогичными результатами в декартовых координатах подтверждают правильность как выкладок, проделанных автором, так и окончательных уравнений.

2.    Вывод уравнений

Рассмотрим стационарное течение несжимаемой среды — жидкого металла. Течение и теплообмен можно описать следующей системой дифференциальных уравнений в векторном виде:

∇⋅V=0,(1)

ρ(V⋅∇)V=-∇p+µΔV+ρf,(2)

ρCp(V⋅∇)T=λΔT.(3)

Здесь: (1) — это уравнение неразрывности, закон сохранения массы жидкой среды; (2) — уравнения движения, закон сохранения импульса; (3) — уравнение для энергии, закон сохранения удельной энтальпии движущейся среды. При этом приняты обозначения: ρ — плотность, p — давление, µ — динамический коэффициент вязкости, λ — теплопроводность, С_p — теплоемкость среды, f — вектор массовых сил (сила плавучести в данной задаче). В этих уравнениях дифференцирование по координатам представляется как оператор ∇ , дивергенция вектора скорости V — как скалярное произведение ∇ ⋅ V , градиент скалярного поля температуры — как ∇ T , лапласиан от скалярного поля температуры — как Δ T , лапласиан векторного поля скорости — как Δ V . Очевидно, что для сплошной среды векторная запись уравнений является наиболее общей и справедлива в любой системе координат.

Задачу течения в кольцевом канале было бы удобнее всего решать в цилиндрической системе координат (ЦСК) O r ₀ ϕ ₀ z ₀, если бы ребро было не винтовым, а прямым (без закрутки). В ЦСК базис e _{0 i} ( i = 1, 2,3) является ортогональным (см. Рис 2 а ), поэтому систему уравнений, используя коэффициенты Ляме, можно записать в хорошо известном тензорном виде [7].

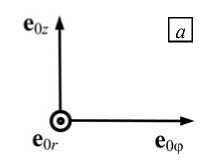
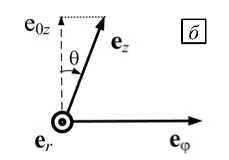
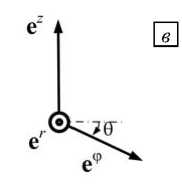
Рис. 2. Векторный базис в различных системах координат: в цилиндрической ( а ), в винтовой прямой ( б ) и обратной ( в )

Если ребро закручено вдоль канала, то задача существенно усложняется. Будет естественным решение задачи в винтовой системе координат, где координатные линии, направленные вдоль оси z , закручиваются вокруг продольной оси канала вместе с ребром, оставаясь параллельными плоскости ребра. В такой системе координаты также выражаются тройкой чисел (r, ф, z), но, в отличие от ЦСК, базисный вектор еz наклонен по отношению к вектору е0z на некоторый угол 9, так что проекция вектора еz совпадает с е0z (Рис. 2б), и базис в ВСК ei уже не является ортогональным.

Введем параметр a , который определяет степень закрутки ребра:

a = 2л/ L ,

где L — шаг закрутки, часть длины оси канала при повороте ребра на угол 2 п . Базисные векторы е _r , е _ф остаются такими же, как и в ЦСК, но надо иметь в виду, что угол в поперечном сечении канала всегда отсчитывается от ребра, и теперь е _ф зависит от координаты z . Тангенс угла 9 вычисляется как tg( 9 ) = ar , а синус и косинус — как sin( 9 ) = ar,^ 1 + ( ar )² , cos( 9 ) = 1, ^/1 + ( ar )² . Преобразование координат из ЦСК в ВСК осуществляется согласно соотношениям: r = r ₀, ф = ф ₀ - az , z = z ₀.

Для дальнейшего изложения требуется ввести некоторые понятия [8, 9]:

• – прямой и обратный базисы; обратный базис e ⁱ находится через прямой e _i путем циклической перестановки индексов ( i , j , k ) (они принимают значения (1, 2, 3)): е ¹ = ( е j х е k )/ ^ e i x ( e j х е k ) ] , и имеет место произведение векторов прямого базиса: в числителе векторное двух векторов, а в знаменателе смешанное трех векторов;

  – ковариантные и контравариантные компоненты [8]; понятия соответствуют нижним и верхним индексам, так что ковариантный базис — это e _i , а контравариантный, обратный ему, — e ⁱ ; вектор r раскладывается по координатам прямого и обратного базисов r = x е i = x i e ¹ , x = ( r , ф , z ); тройка векторов обратного базиса показана на рисунке 2 в : е ^r совпадает с е _r , е ^z совпадает с е _{z 0}, вектор е ^ф наклонен по отношению к е _ф на угол - 9 .

Свойства системы координат представляются как скалярное произведение базисных векторов и выражаются метрическим тензором g_ij . Для ковариантного базиса в винтовой системе координат запишем:

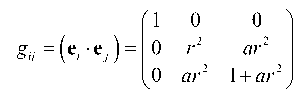
0 )

Определитель матрицы метрического тензора имеет вид: G = | g ij | = r ² . Если параметр закрутки a принять равным нулю, то тензор g_ij превращается в метрический тензор для ЦСК.

Для обратного (контравариантного) метрического тензора справедливы формулы:

( 1       0

0 )

gij

= ( е ¹ ■ е j ) = 0 | — + a v / I r

0 — a

G - ¹ = | g j | = 4.

r ²

Скалярное произведение векторов прямого и обратного базисов по определению равны единичному (шаровому) тензору: g‘ j = ( e ¹ x e j ) = S j (0 при i * j и 1 при i = j ).

Вектор можно разложить по ко- и контравариантному базисам, при этом его компоненты будут, соответственно, контра- и ковариантными. Представляют интерес контравариантные компоненты вектора скорости, как результат разложения по векторам прямого базиса: V = V¹ е i , V = ( V^r , V ^ф , V z ) .

На практике используются «физические» компоненты вектора V * ¹ , которые имеют одинаковую размерность (м/с) V = ( V * ^r , V * ^ф , V * ^z ) [8]. Связь с физическими компонентами осуществляется через диагональные члены метрического тензора g_ii (по i не суммировать!):

JZ *'

V' = V= gii

.

В обсуждаемом случае удобно представить вектор смешанными компонентами V = (V^r , V * ^v , V z ).

Частная производная вектора по координате в криволинейном базисе выражается следующей формулой:

dv = д(^еу) = 8 vJ + дxk     дxk     дxk J      дxk

Разложив производную вектора по контравариантным компонентам, получим тензор скоростей деформации:

V ' =^ Ve‘ = ^д V J + V^Jr*

• k a x^k       a x k         ^j

Здесь введены символы Кристоффеля [8, 9], которые определяют разложение производной базисного вектора по базису:

. de j

Г '_к = e 'J .

^Jk        d x k

Символы Кристоффеля Гⁱ_jk можно рассчитать непосредственно по формуле (8), либо через производные метрического тензора [8]:

iim

Jk g        m , Jk

im 1 fdgJm   9gmk   9gJk J g1.

2 (d x^k     a x^J    a x^m J

В ВСК символы Кристоффеля (отличные от нуля матрицы) имеют такой вид:

¹ Г _jk

de e ■ ax'

f ^{0   0     0} J

0 - r - ar

₍ 0 - ar - a ² r _?

_{d e} f 0 V ^{r  a}l^r j

Г 2k = e ’— J = V r  0   0

jk k дx (a/r   0    0 J

Тогда уравнения сохранения (1)–(3) можно представить в тензорном виде (см. [8]):

V k = 0, p ( v^ v J ) =- g k d p +ц g km (V , m ) , k +p f,

P C P V ■

d t J d x^{J J}

Член в уравнении (2), связанный с вязкостью — p A V , определяется через тензор скоростей деформации

V_,ⁱ_k , если взять ковариантную производную от тензора по правилу, взятому из монографии [8]:

д(Vi )

( ^v m ) , k = 4^ ⁺ ( ^v m Ь Г ;. - ( ^V', v ^r km

Вывод уравнений (12) наиболее трудоемок, но не сложен. Контравариантные компоненты объемных сил находятся согласно соотношениям: fⁱ= fe ⁱ .

Теперь рассмотрим результат преобразования системы уравнений (9)–(11) в ВСК. Для «физических» компонент вектора скорости V = ( V * ^r , V * ^ф , V * z ) нужно будет учесть разложения (8). В случае винтовой системы координат это необходимо сделать только для компоненты скорости V * ^ф , которая далее

обозначается как V ^ф (индекс «*» опускается). В уравнениях можно выделить два вида членов: слагаемые, не связанные с закруткой потока, такие же, как и в ЦСК, и добавочные члены, в которые входит параметр закрутки а . Уравнение неразрывности (9) по виду остается точно таким же, как и в ЦСК. В левой, конвективной, части уравнений трех уравнений для проекций импульса (10) появляются следующие члены:

i = 1,                     р ( V^z ■ V^z ■ a ² ■ r + V ^ф - V^z ■ a ) ,

i = 2,                           p(-Vr ■ Vz ■ 2a), представляющие собой инерционные силы, возникающие во вращательной системе координат: центробежная сила и компоненты кориолисовой силы. Эти силы компенсируются градиентом давления, добавочные компоненты которого в правой части трех уравнений для проекций импульса (10) имеют вид:

i = 2, i = 3,

д p 2   д p

— a r +--ar, дф     дr дp a.

дф

Дополнения (13)–(16) вносят наиболее существенный вклад в уравнения. Остальными членами, которые входят в вязкий член в случае, когда степень закрутки невелика, то есть параметр a достаточно мал, при решении задачи будем пренебрегать.

Ниже приводятся добавочные члены в уравнениях движения (10) в ВСК для компонент силы вязкости p g km (V ‘_m ) k (коэффициент ц внесен под знак производной для последующего перехода к осредненным уранениям — уранениям Рейнольдса):

i = 1, i = 2, i = 3,

-4 (дф	f д vr ц^ ( д z	1+^f J д z	д Vr 1 ц г дф )	] a	-	<д ( ц Vz )     д Vr' —--- + ц-- дф     дф	a +Af r дф(	д V r 1 2 ц--- a дф)
-f-f (дф1	д V ф Ц д z	!+—f ) д z (	д V ф 1 ц г дф )	] a	-	"д ( ц Vz )     д V r 1 —--- + ц-- д r       д r (                    )	a +4 r дф[	д V ф1 2 ц-----I a дф )
	-(	д f ^“I ц дф(	д Vz 1 ------I + д z )	^[ д z (	ц	д Vz 11     д f д Vz 1 2 —— | a +—I ц—- | a дф ) I дф ( дф )		.

В уравнении сохранения энергии (11) левая — конвективная — часть остается такой же, как и в ЦСК, а справа появляются новые члены:

д L дTA д f, д T 11 I X I +—I X I I дф ( д z ) д z ( дф ) )

д L д T 1 ₂ a +--1 X— | a . дф( дф )

3. Численный расчет

Далее кратко представлены результаты предварительных расчетов в ВСК поставленной задачи. Отношение диаметров внутренней и наружной труб составляло d 1 / d ₂ = 12/27 мм/мм, длина канала — 1 м [1], зазор между ребром и внешней трубой — 0,75 мм.

Уравнения (9)–(11) приводилиcь к безразмерному виду и для осредненных переменных имели вид:

– уравнение движения

Gr

( V -V ) V = -V p + — V- 1 + -^ V V + — 0 g ;

^х ' Re ( ( и) )      Re²

– уравнение энергии

( V ■V ) 0 =

1 „ , Pr L „ --V d 1 +--- t | V 0 .

Re Pr   ( Pr t J

Здесь: p * — динамическое давление, отнесенное к масштабу rV ₀²; - t — коэффициент турбулентной вязкости; и — кинематический коэффициент вязкости; число Рейнольдса Re = V 0 d /v , число Грасгофа

Gr q = g β q с d 4 ( λν 2 ) , число Прандтля Pr = µρ C p /λ , турбулентное число Прандтля Pr t = ε t /ε _q ; Θ — безразмерная разность температур, которая рассчитывалась по формуле Θ = ( T - T ₀ )/( q_cd λ ) . В этих выражениях: g ^* = g/ g — безразмерный вектор силы тяжести; g — ускорение свободного падения; β — коэффициент термического расширения; q_c — плотность теплового потока на стенке внутренней трубы; ε q — коэффициент турбулентного переноса тепла; T — температура жидкости; T 0 — температура на входе в трубу. Масштаб для координат r и z принимался равным эквивалентному диаметру кольцевого канала d = d ₂ - d ₁. Компоненты вектора скорости V относились к средней по сечению канала скорости V ₀ . На входе в канал профиль скорости считался единичным: | V | = 1. На выходе из канала обеспечивалось условие постоянства расхода. Тепловой поток на стенке задавался в безразмерном виде выражением qc ^*= 1 Pe( ∂Θ ∂ R ) _с = - 1Pe. Внешняя стенка канала была адиабатической ( q_c = 0 ). Турбулентное число Прандтля составляло: Pr _t = 1 .

При численном решении задачи расчетная сетка имела, соответственно, размеры N_r × N _ϕ × N_z = 60 × 50 × 450 и вблизи стенок сгущалась. Ее вид в сечении канала показан на рисунке 3.

Система уравнений (20), (21) с учетом уравнения неразрывности (1) решалась в пакете численного моделирования процессов гидродинамики и тепломассобмена ANES20XE [10]. Вводился коэффициент турбулентной вязкости ε t по формулам Рейхардта [7], адаптированным к кольцевому каналу. В формулах Рейхардта (для трубы) в качестве диаметра берется ширина кольцевого зазора d = d ₂ - d ₁, а расстоянием до стенки считается расстояние до ближайшей из стенок. Такой подход оправдал себя при моделировании течения жидкого металла (ртути) в прямых трубах и каналах некруглого сечения [11].

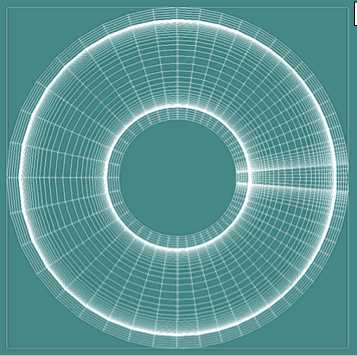
Рис. 3. Расчетная сетка в сечении кольцевого канала с ребром ( а ); стенки канала и ребро ( б ) (выделены белым цветом).

б

В расчете учитывалось влияние термогравитационной конвекции. Вектор силы плавучести в уравнениях Gr q 1 ∂Θ Gr q ∂Θ                                        7

• (10) определяется компонентами: (0, - cos( θ )          ,        ). В расчете принималось, что Gr = 2 ⋅ 10⁷ .

0.0817

Re² r ∂ϕ Re² ∂ z                                 ^q

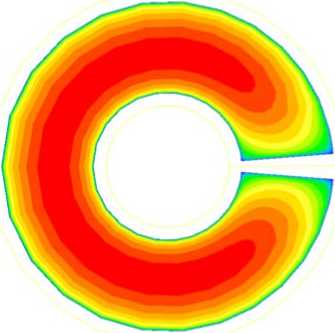
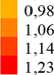
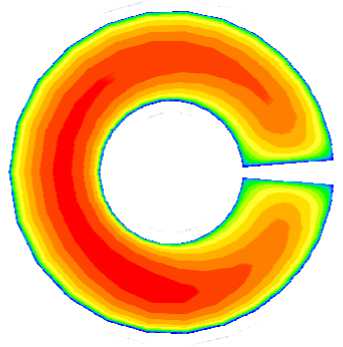
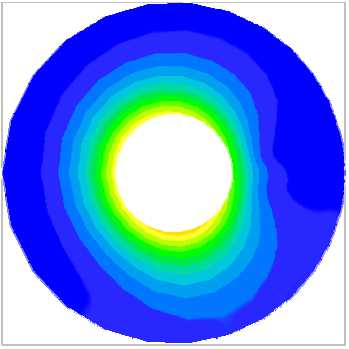
Далее на рисунке 4 показаны характерные результаты, полученные для сечения канала, удаленного от входа на 65 d для прямого ребра и ребра, закрученного против часовой стрелки (безразмерный параметр закрутки равнялся а = 0,2 ) при отсутствии зазора между внешней стенкой и ребром . Так как параметр закрутки мал, то поправки к диффузионым членам (17)–(20) в решаемой системе уравнений (1), (20), (21) также были малы и в расчет не вводились (хотя их учет не составляет большого труда). Пересчет компонент скорости из ВСК в ЦСК (обозначены индексом «⁰») осуществлялся по формулам: V ^{0 ϕ} = V ^ϕ + aV^z , V ^{0 z} = V^z .

Результаты показывают, что без закрутки потока поля скорости и температуры оказываются симметричными, и распределение температуры стенки по периметру канала имеет максимумы вблизи ребра. При закрутке потока появляется азимутальное течение, нарушающее симметрию полей скорости и температуры, а распределение температуры стенки кардинально меняется. Вблизи ребра теперь температура минимальна, а максимум наблюдается на стенке в точке с координатой ϕ ≈270°, отсчитываемой от ребра в сторону закрутки.

а

0,163

0,245

0,327

0,409 0,49

0,572

0,654

0,735

0,817

б

-0,0353

-0,02 -0,0047

0,0105

0,0258

0,041

0,0563

0,0716

0.0868

0,102

0,117

0,133

0,148

0.163

0,178

0,194

О 0,0859 0,172 0,258 0,343 0,429 0,515 0,601 0,687 0,773 0,859 0,945 1,03 1,12 1,2 1,29

1 -0,043

-0.0248 -0.00655

0,0117

0.0299

0.0481

0.0664

0.0846

0.103 0,121

0,139 0.158

0,176 0,194 0,212

0,23

Рис. 4. Поля продольной компоненты скорости V z ( а , в ) и безразмерной разности температур © ( б , г ) в сечении z = 65 d кольцевого канала при отсутствии зазора между ребром и внешней стенкой при Re = 30000 и Gr = 2 - 10 7 в случае прямого ( а , б ) и закрученного ( в , г ) ребра

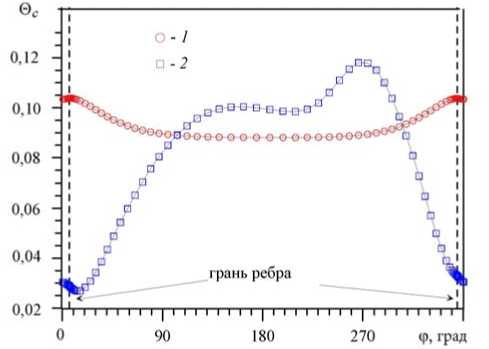
Рис. 5. Распределение по периметру сечения канала безразмерной температуры © _с обогреваемой стенки в отсутствие зазора между ребром и внешней стенкой: ребро без закрутки, а = 0 ( 1 ); закрученное ребро

Несмотря на большой шаг закрутки, азимутальная продольной компоненты V ^{0 z} (Рис.9).

Расчетные данные для канала с зазором между ребром и внешней стенкой содержат рисунки 6–8. Несимметрия в полях скорости и температуры здесь еще более заметна. При этом наличие зазора незначительно сказывается на распределении температуры стенки в канале при прямом ребре, в то время как при закрученным ребре (Рис. 7) эту несимметрию усиливает. Максимум в распределении © c смешается к углу ф~ 210 ° , что связано с влиянием струи жидкости, проникающей в зазор.

Распределения безразмерной разности температур © c по периметру сечения канала при закрученном ребре и зазоре между внешней стенкой и ребром для разных чисел Рейнольдса показаны на рисунке 8. Форма графиков для значений чисел Рейнольдса из диапазона 10000–50000 примерно одинакова и несколько отличается для Re = 5000, что, по-видимому, связано с относительно большим влиянием сил плавучести вблизи обогреваемой стенки. скорость V ^{0 ф} достигает 20%-ной величины от

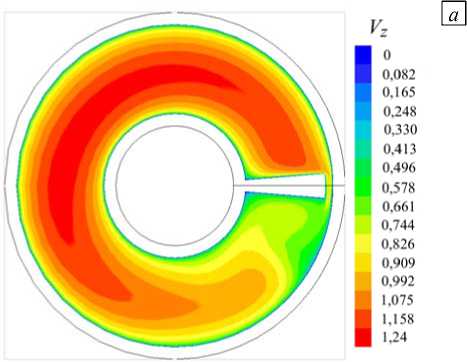
Рис. 6. Поля V z и 0 в кольцевом канале с закрученным ребром при наличии зазора между ним и стенкой

О            90           180          270   <р, град

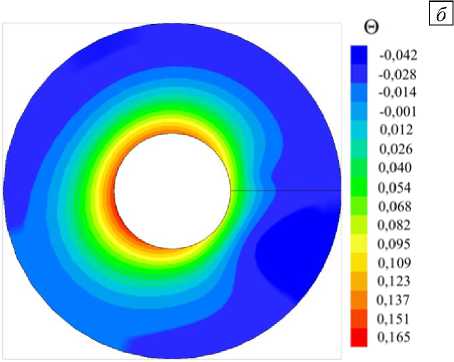
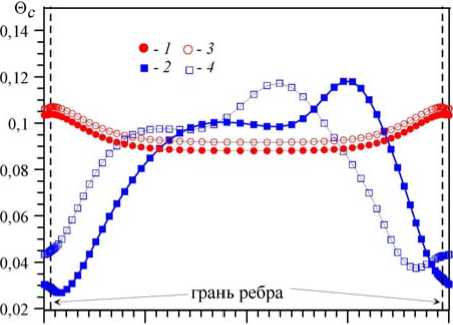
Рис. 7. Распределение безразмерной температуры 0 c обогреваемой стенки по периметру сечения канала при ребре без зазора (символы 1 , 2 ) и с зазором (символы 3 , 4 ) в канале с прямым ( а = 0) ( 1, 3 ) и закрученным ( а = 0,2 ) ( 2 , 4 ) ребром

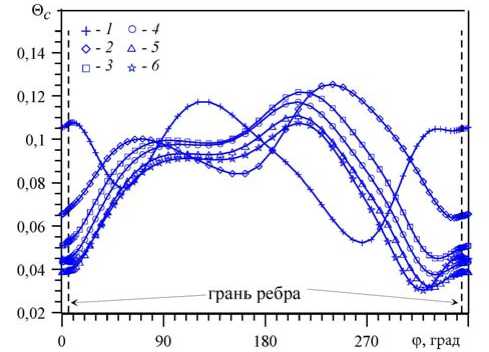
Рис. 8. Распределение безразмерной температуры 0 c по периметру сечения канала при ребре с закруткой и зазором для разных значений числа Рейнольдса Re : 5000 (кривая 1 ), 10000 ( 2 ), 20000 ( 3 ), 30000 ( 4 ), 40000 ( 5 ), 50000 ( 6 )

Рис. 9. Векторное поле азимутальной скорости V ° ’ в сечении канала

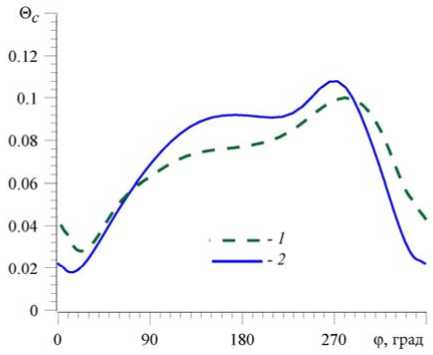
Рис. 10. Распределение по периметру сечения канала с закрученным ребром ( а = 0,2) безразмерной температуры обогреваемой стенки, при Re = 50000 : данные расчета в декартовой системе координат из [2] (кривая 1 ); авторский расчет в ВСК ( 2 )

Для сопоставления на рисунке 10, кроме авторских результатов численного моделирования задачи конвективного теплообмена, полученных в ВСК, приведены распределения безразмерной температуры обогреваемой стенки по периметру сечения в канале с закруткой ребра (без зазора) для режима течения с числом Рейнольдса Re = 50000 (данные из [2]). Видно, что данные хорошо согласуются, а различия связаны с разными моделями турбулентности, принятыми в расчетах.

4.    Заключение

Для численного расчета гидродинамики и теплообмена в каналах с винтовой геометрией предлагается разрешающую систему дифференциальных уравнений, записанную в цилиндрических координатах, преобразовать в систему в винтовых координатах.

Преимущество винтовых координат заключается в простоте описания геометрии расчетной области, поскольку появляется возможность использовать структурированную расчетную сетку, упрощается задание граничных условий, удобным становится вывод результатов для анализа и последующей обработки. Применяется алгебраическая модель турбулентности, зарекомендовавшая себя в прямых каналах с жидкометаллическими средами. Все это позволяет существенно экономить вычислительные ресурсы, сокращает время расчета и способствует получению более надежных расчетных данных.

Переход к винтовой системе координат осуществляется путем введения в записанные в цилиндрической системе координат уравнения члены, связанные с закруткой канала. Формулы и вывод необходимых добавочных членов представлен в статье.

В соответствии с описанной методикой проведен расчет гидродинамики и теплообмена при течении жидкого металла в кольцевом канале с винтовым ребром. Обнаружено и продемонстрировано влияние закрутки потока на характеристики теплообмена.

Работа выполнена при финансовой поддержке Российского научного фонда (грант № 14-50-00124).