Решение задачи о деформировании термоупругой пластины методом быстрых разложений

Математическую модель для термоупругой пластины представим следующей системой относительно поперечного перемещения w и температуры T _:

Запишем граничные условия:

w|

I x = 0

a ²w д5с²

= wL

x

x = 0

д 2w д5с2

4 ^w

(ax4

2 ' w a x² a y ²

~

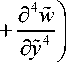
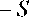
a w a w i

+I +

(dx2 ay2)

dw дy2

= w| y=0

ajw дy2

= w| = wy=0

a              (2)

= 0

2л

+ ^{k w} = q ( y ) - Y — +-2-I+ a ( ^T - T o ) .

(dx    dy ) x '(1)

а² т a ² т   - - / - x

+ — + E_o + E1 ( T - T o ) = 0.

ax    ay

(x. y )eQ ([0. a ] x [0. b ])

где Y . a - параметры. характеризующие тем

пературное расширение. T _o - начальная темпе

ратура. к - коэффициент упругой постели. S - удельное усилие растяжения пластины по контуру. q ( y ) - интенсивность равномерно

Для представления задачи в безразмерном виде введем следующие обозначения w = w ₀ w . x = ax . y = by .      S = SD/ a ² .      fc = R D, a ⁴ .

^q ( y ) = = q ( y ) ^w 0 ^Dl^{a 4}.               ^E i = ^E i/ ^{a 2}.

Y = Y W 0 D /( T 0 a ² ) . c c = a w 0 d/ ( T 0 a ⁴) . T¹ = T 0 T . Ё₀ = T ₀ E ₀/ a ² . где величины без тильды сверху являются безразмерными. Тогда система (1) принимает форму:

4      2   4      44

д w a д w a д w --  + 2 — ;   + —;-- --дx⁴      b ² д x ²а y ² b⁴ ay⁴

распределенной нагрузки , которая будет

- S

определена ниже. D - жесткость пластины

" a² w _{+ (} d x ²

a ² a ² w I b? day² J

+ kw =

при изгибе. выражение E ₀ +

E i ( T - T )

опре-

= q (y)-Y

деляет внутренний источник саморазо-гревания, представленной линейной зависимостью от температуры.

"a2 t + (dx2

a ² a ² T I b² a y ^{2 J}

+ a( T -1).

a2 t ax2

a² a²T b² a y²

+ E0 + Ei (T -1) = 0.

( x . y ) e n ( [ 0.1 ] x [ 0.1 ] )

Вестник^ВТУИТ, №2, 2013

Граничные условия (2) в безразмерном виде:

w

d² w d x ²

= w|

d² w d x ²

= w|

5² w

5 y ²

= w|

5² w

5 y ²

= 0

Быстрое разложение в форме (8) подставим в (3) и в граничные условия (4):

N

A5 (У)(1 — x) + A6 (У)x + Z Wm (У) m4П4 • m=1

• sin ( m n x ) + 2— ( A 3' ( y )( 1 — x ) + A 4 ( y )

Решение задачи приведено далее.

Для функции T ( x , y ) в [1] был получен ее аналитический вид:

+ A 5" ( У ) T V ²

x ³

--—

x | + A 6 ' ( y ) ^x-7 3 7 I 6

--—

E

T ^{( x} , У ) = ^{1 +} у ( ^x

—

x ²

N

2 E 0

^{) +} Z L m n

— e

I   a 4

^— Z W m '( y ) ^{m n} sin ( ^{m n x} ) |⁺yr ( A 1 ( y ) • m = 1                             7 b

•

E 1

L E 1

—

2_2 m n

+ 1

—

E 1

E 1 — m П ²

•

, x x

• ( 1 ^{— x} ) + A 2 ( У ) ^x + A 3 ( У ) l —

--—

+

22 b

V m n - E_v- y e ^a

mn/E . • b

1 + e ^a

+

e

b

—

a

_л    — T m ² ? ² — E 1 • b

1 + e ^a

sin ( m n x )

+ A 4 ( y ) x — X 1+ a 5⁴⁾( y ) •

•

Представим w ( x , y ) быстрым разложением по синусам в виде суммы граничной функции M 4 w ) ( x , y ) (так как дифференциальное уравнение для w 4-го порядка) и быстро сходящегося ряда Фурье [2]-[3]:

N w (x, У) = M 4w) (x, y) + Z Wm (У) sin (mnx), (6) m=1

M ^4 ^w ) ( x , y ) = w ( 0, y )( 1 — x ) + w ( 1, y ) x +

— — ---— + — + A (4) ( y )•

24 120 18 45 7   ⁶

5 x 3 7 x

•

----1--

120 36 360

N

+ z W m ) ( y ) sin ( m ^{n x} )

m = 1

—

^{— 5} ( A 3 ( У )( 1 ^{— x} ) ⁺ A 4 ( У ) ^{x +} A 5 ( У ) •

23 x x

•

— -- —

( 2 6

x I , / \ x л I + A6(У)

3 7 I 6

--—

N

Z W m ( У ) • m = 1

⁺ w xx ( 0, у ) x r

x

--—

^x ₇  ⁺ w xx ( 1, У ) •

• mП? sin ( m n x ) + pr( A " ( У )( 1 — x ) +

7 з >  x x

•

—

V ^{6 6} j

+ xxxx

—

x ⁵ x ³ x I ⁽⁷⁾

A 2 ( y ) x + A 3 ( y ) l ^x ₄

— -- —

X J+ A 4 ( у ) •

--—

— + — +

24 120 18 45

x ³ 7 x

120 36 360

Для удобства дальнейших рассмотрений обо-

значим     w ( 0, y ) = A 1 ( y ) ,

w xx ( 0, У ) = A 3 ( У ) , w xxxx ( 0, У ) = A 5 ( У )

w ( 1, У ) = A 2 ( У ) , w x ( 1, У ) = A 4 ( У ) ,

, w xxxx ( 1, У ) = A 6 ( У ) .

Тогда представлени е (6) примет форму: w ( ^x , y ) = A ( y ) ( 1 ^{— x} ) ⁺ A 2 ( y ) ^{x +} A 3 ( y ) •

[ x ² x ³

•

^x I+ A;( y ) — 6 7

•

V ²

x

--—

x

--—

24 120 18

X 3 X |

—+— |+

7 x

+ A ‘ ( У ) —

6V 4120 36 360

—

N

+Z w:( y )• m=1

• sin ( m n x ) ) ) + k ( A 1 ( y )( 1 — x ) + A ( y ) x +

⁺ A 3 ( У ) f V ²

x ³

--—

x I ; / \ x - |⁺ A 4 ⁽ У ) -

3 7 I 6

+A (y) — v x 24 120 18

--—

— I + 6 7

45 J+ A 6 ( У ) •

•

x + A 4 ( У ) ^x- — x + A 5 ( У ) •

—

3 7 x

N

\

x

x

24 120 18 45

x ⁵ x ³ 7 x

1 0 36 360

⁺ A 6 ( У )

120 36 360

⁺ Z ^Wm ( у ) sin ( m ^{n X} ) =

m = 1

N

⁺ Z ^Wm ( У ) sin ( ^{m n X} )

m = 1

, x [5² T

= q ^{( y )— Y}\dx? ⁺

a ² d² T

b ² d y ²

4=о d ² w d x²

= A ( y ) = 0, w x = 1 = A 2 ( y ) = 0,

x = 0

3 2 w

= A 3 ⁽ y ^{) =} 0,   ..

= A 4 ( y ) = 0

в виде суммы граничной функции нулевого порядка M 0 ^F ) ( x , y ) , M 0 ^P ) ( x , y ) и ряда Фурье, т.е.:

W y = 0 = A 5 ( ⁰ ) [ 24 -

x ³    x )

18 45 J

+ A 6 ( 0 ) -

7 x ) ---1--+

360 J

N

^ W m ( 0 ) sin ( m n x ) = 0, m = 1

F ( x , y ) = F ( 0, y )( 1 - x ) + F ( 1, y ) x + + IX ( У ) sin ( m n x ) ,

P ( x , y ) = P ( 0, y )( 1 - x ) + P ( 1, y ) x +

⁺ £ ^P m ( У ) sin ( m n x )

m = 1

„ f _x ⁴

W = A ₅ ( 1 )

^{1 y} = 1      ^{5V 7}( 24

x ³    x )

18 45 J

+ A ( 1 ) -

Y 5    Y3     7 Y ^ _N.

----+--- + YWm (1) sin (mnx ) = 0, (120 36 360 J ml mV }} d2 w ,„/„x( x4   x5   x3

——   = A’ (0)

d y ²_n^{5V 7}U4 120 18 45

y=0x

A ( 0 )1 — ^6V 120

-

x3

--1+

36 360 J

N

+^ Wm (0) sin (mnx) = 0, m=1

Из равенства (12) следует равенств о коэффициентов разложения в (13), т.e. F ( 0, y ) = P ( 0, y ) , F ( 1, y ) = P ( 1, y ) , F m ( y ) =

=Pm (У), m = 1,...,N. Для получения этих равенств необходимо в (9) положить x = 0 и x = 1, а также умножить (9) на sin(nnx), n = 1,...,N и проинтегрировать по переменной x e[0,1].

Согласно вышеизложенным рассуждениям из

(9) при x = 0 и x = 1 найдем:

d ² w .„xd x ⁴    x ⁵    x ³ 7 x

—— = A’ (1)------1-- dy2 ,   ^^ 24 120 18 45

^V y = 1             x

A 5 ( у ) = q ( у ) ⁺ Y E 0 , A 6 ( у ) = q ( у ) + Y E 0 ⁽¹⁴⁾

Из (14) при у = 0 и у = 1 получим:

A « ' ( 1 )

x ⁵ x ³ 7 x | ----1--+

120 36 360 J

N

+ ^ W m ( 1 ) sin ( m n x ) = 0

m = 1

К уравнению (9) применим метод быстрых разложений [2], который заключается в следующем. Обозначим левую и правую части (9) через F ( x , y ) и P ( x , y ) , т.е:

^F ( x , y ) = P ( x , y )                ⁽¹²⁾

Равенство (9) должно выполняться при любых значениях x e[0,1], y e[0,1]. В этом уравнении присутствуют четвертая и более младшие производные от ряда Фурье из (6). Так как ряд Фурье в (6) строился с граничной функцией четвертого порядка M4w)(x, y), то этот ряд вместе со всеми четными производными до четвертого порядка включительно точно сходится на границе при x = 0 и x = 1;

шестая производная от этого ряда внутри интервала ( 0,1 ) сходится, а на границе может расходиться. Поэтому F ( x , y ) , P ( x , y ) следует представить быстрым разложением по синусам

A 5 ( 0 ) = A 6 ( 0 ) = q ( 0 ) + у Е 0 , A 5 ( 1 ) = A 6 ( 1 ) = q ( 1 ) + у Е 0

Чтобы воспользоваться равенством

Fm (У) = Pm (У), m = 1,...,N,    предварительно определим функцию q (y). Стороны прямоугольной области Q при x = 0 , x = 1 разобьем на три участка с помощью искусственно введенной малой величины 8

0 <  У <  8 и 8 <  У <  1 - 8 U 1 - 8 <  У <  1 (16) Функция q ( у ) должна удовлетворять условиям согласования граничных условий (4) и первого дифференциального уравнения из (3). К выражениям (11) применим оператор быстрых разложений 4-го порядка. Для этого от условий при у = 0 , у = 1 возьмем производные по x нулевого, второго и четвертого порядков . В получившиеся уравнения подставим x = 0, x = 1, а также умножим их на sin ( n n x ) , n = 1,..., N и проинтегрируем по переменной x e [ 0,1 ] . В результате получим:

А 5 ( 0 ) = 0, А ( 0 ) = 0, W m ( 0 ) = 0, m = 1,..., N ,

А ( 1 ) = 0, А б ( 1 ) = 0, W m ( 1 ) = 0, m = 1,..., N , A 5 ( 0 ) = 0, A ^ ( 0 ) = 0, W m ( 0 ) = 0, m = 1,..., N ,()

■ ( 1 ^-(" ‘ ) ⁿ ) + 25? ^{W ;}( у ) )+ ^k

' ( 1 ^{-(- 1 ) n} )

n ^sn ⁵

k

■

A 5' ( 1 ) = 0, A 6 ( 1 ) = 0, W m ( 1 ) = 0, m = 1,..., N

Условия согласованности будут выполнены, если зависимость q ( y ) не приведет к противо-

■ ( q ( y ) + Y E 0 ) + — ( y )

² 7

= -Y 1

¹² a ² t

a ² d ² T )

■

d x ² b ² d y

речию в угловых точках прямоугольной области. Отсюда вытекают следующие равенства:

q ( 0 ) = - / E ₀ , q ( 1 ) = - / E 0 ,           (18)

q ( ^£ ) = q 0 , q ( 1 ^- £ ) = q 0               ⁽¹⁹⁾

■ sin ( n n x ) dx + a j ( T - 1 ) sin ( n n x ) dx

В результате получим обыкновенные диффе-

q' ‘ ( 0 ) = 0, q' ' ( 1 ) = 0

q' (£ ) =... = q (4)( £ ) = 0, q'(1 - £) =... = q(4) (1 - £) = 0

ренциальные уравнения четвертого порядка от одной переменной y . Для решения этой системы повторно применим метод быстрых разложений к каждой из н еизвестных функций W_n ( y ) ’ n = 1’...’ N . С этой целью сначала пред

Одна из простых зависимостей функции q ( y ) ,

которая удовлетворяет полученным условиям (18)-(21), имеет следующий вид:

,          . 3 ( y - £ ) ⁵

q 0 + ( q 0 + Y E 0 )      5 ⁷ +

£

+ ( q 0 + Y E 0 ) 2^{( y} _£ 6 ^{£ £}

ставим W_n ( y ) ’ n = 1’...’ N разложением по синусам в виде суммы граничной функции M 4 Wⁿ ) ( У ) и ряда Фурье:

N w. ( у )=M 4Wn)( у )+Ё w. ’ isin (ln у )      (24)

l = 1

M 4 ^Wn ) ( У ) = W n ( 0 )( 1 - У ) + W n ( 1 ) У +

', ,2 „3                   ' „3

w :( 0 ) — -—- y + w ,"( 1 ) — - y ⁿ 263 ⁿ 66

+

k

q ( у ) ^=<

q ₀ npu £ <  y <  1 - £ ,

+ w 4⁴⁾ ( 0) — - — ^{n v} Л 24 120

—

^y- +

18 45

Для

q 0 + ( q 0 + Y E 0 )

³ ( У ^{- 1 + £} ) ⁵

⁺ Y E 0 )

2 ( y - 1 + £ )'

£ 5

⁺ ( ^q 0 ⁺

+w44)(1)' -— n V k 120

yL ₊ ⁷ y '

36 360 ₇

£ ⁶         ’

npu 1 - £ <  y <  1 реализации

^F m ( У ) = ^P m ( У ) ’ m = 1,..., ^N

равенства умножим (9) на

sin ( n n x ) ’ n = 1’...’ N и проинтегрируем по пе

ременной x е [ 0’1 ] :

А ( 1 - ( - 1 ) " ) + w . ( у ) ”4 - ^ ■ n n                2 bn n

■ ( 1 ^{-(- 1 )} ) - b ^{n П 2} W n "⁽ y ^{) +}

a ⁴ q ^{( 4 )}( y ) b⁴ n П ⁵

' iX ⁿ

■ ( 1 - ( - 1 ) ⁿ ) + ^W4 У ) - ^s yj

k

/ 7 \ x 7 X n П ² a ² q "( y )

■⁽ q ⁽ y ^{) +} y ^e 0 ^)- W n ⁽ y )—+ 2 / 2 bn n

Тогда представление (24) с учетом (17) примет более удобную форму:

'1,4

W ( y ) = W ^{4 )}( 0 ) y-^nV' ^{n v 7}I 24 120

y ⁵

---

y

y

' v"    v^:         A N_

+ W k (1)----¹-- + ^EWn /sin ( ln y)

^{n (} ) k 120 36 360 J ^ZY1 ⁿ’l ⁽ )

Найдем функции W _n "( y ), W _n ⁽⁴⁾( y ):

'1,2     i,3

w ;( у ) = W n ⁽^*(0) v - y7

k 2    6

+Wn'4,(l) У -y k 6 6 7

y

+

_N                  (27)

- ^ W n i^² n ² sin ( l n y )

i = 1

W ,⁽⁴⁾( y ) = W n ⁽⁴⁾( 0 )(1 - y ) + + W „ ⁽⁴⁾( 1 ) y + ^^ W _nl l 4 П ⁴ sin ( i n y ) l = 1

Подставим в (23) выражения (26)-(28): 44     45

LEo. i - ( - 1 ) ⁿ + n^, w W( o ) y_ — 2_ — n n ^{( V} ’ )    2 ( n \ 24 120

Теперь в (23) положим y = 0 и y = 1

Y-E0- (1 -(-1)")

nn v         7

360 a ⁴ ( q 0 + y E 0 ) £ ⁴ b⁴n ⁵K ⁵

- У3- + yL 18 45

■ V w ^⁴⁾(1) Г y

) n ^V 120

-

y ³ 7 y

a * W . ^W'( 0 ) =

120 36 360

N

• E W n , 1 sin ( ^{l n} y ) |^-

-

1 = 1

2 a 22 — n П b ²

2 a ² q "( y ) b ² n ^Зк ³

-

( W , "'( 0 ) l у - у - y 1 + W . ^|4,(1) ^

= -Y j

^1Л5² T

2 b ⁴

a² d ² T

d x ² b ² 9 y ²

sin ( n n x ) dx

y = 0

•

y ³ 6

y I n             I

-тЬЁWn, 11 n sin(1ny) |

⁶ ) 1 = 1                        )

a⁴ q ⁽⁴⁾( y )

b ⁴ n П ⁵

+ a j( T -1) sin (nnx) dx

y = 0

■ ( 1 ^{-(- 1 ) n} ) ⁺ 2 b 4 ( W n ^{(4)( 0 )( 1 -} y ^{) +}

+ W _n ⁽⁴⁾( 1 ) y + 1L W _nj l 4 ^{Л 4} sin ( l n y ) J-

1 = 1      ’                           )

l E t ( 1 - ( - 1 ) ⁿ ) + nn ^{V         /}

■ (1 -("*)n) + 2b4

360 a ⁴ ( q 0 + y E 0 ) £ ⁴ b⁴n ⁵K ⁵

W n ⁽⁴⁾( 0) =

- S

33 n П

(q (y) + YE0 )-

22 n П

=-Y j

^1Л5² T

a ² d ² T

d x ² b ² d y ²

sin ( n n x ) dx

•

y = 1

к

■ W,w( 0) ^

-

y ⁵

—

к

24 120 b

by ³ ₊ b ³ y 18   45

+ a j( T -1) sin (nnx) dx

Из (30)–(31) следует, что:

y = 1

w<4>(0)=W ^ll: 720(q05+ yE0)

£ n К

+W^4)(1)f y5-      ■ n 120 36 360

-

y ³ 7 y

N

⁺ E W n , 1 ^sin

1 = 1

(lny)J+a№ (1 - (- 1)n) + ) bn n '

■

a

2 b ²

к

W n ⁽⁴⁾( 0)      - y r - y | + W n ⁽⁴⁾(1) ^

к 2 6 3 )

■ ((-1)n-1) (32)

В соответствии с методом быстрых разложений, получившееся дифференциальное уравнение (29) умножим на sin ( к к y ) , k = 1,..., N и проинтегрируем по переменной y е [ 0,1 ]

y ³ 6

y I n

^- 7 | Z W n , I l ^{n sin} ( ^{l n} y )

⁶ )    1 = 1

Y E 0 nk n²

44 n к +----

Г w.(4)(0) ■ к k 5K 5

+ k

n П ⁵

( q ( y ) + y E o ) + 2 ( W.^W ( 0 ) ^

—

■

■

к y4

y ⁵

--—

24 120

—+— | +WкОУ

18 45 J

—

V ⁵ y³ 7 у |                      x

---— + — +У W„ ,sin ( 1 k y ) 120 36 360 J £ ⁿ ’ ^{1 v }}

= -Y j

¹ V² T a ² d² T

d x ² b ² d y ²

sin ( n n x ) dx +

+a j (T -1) sin (шхх) dx

2 a ²

b ² n ³ k ³

a ²

—7 n К b ²

a ⁴

(1 -(-1)" )j q'(y)sin (kn-y )dy -

b ⁴ n ⁵ k ⁵

a ⁴

⁺ 2 b ⁴

W ^{( 4 )}( ⁰ )

к п x

w^^ - ^ n , k    2

(1 -(-1)") j q(4) (y) sin (kny) dy 0

W ^ ( 1 - ( - 1 ) k ) + W nk ^ ^ k n                  2

+

- 5

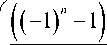
n ³ n

J q ( y ) sin ( k n y ) dy

Y E о n ³ k n ⁴

” Ul ^{n n f} W n 0 ) ' ^{( 1} - ( - 1 ) ^{)( 1} - ( - 1 ) ^{) -}—^ , .• _■ ■ ( 1 - ( - 1 ) ^k ) ⁺ W k ]+ J- ( 1 - ( - 1 ) " ) ■ n П

₊ a f W4 0 ) 2 b ² V k n ³

• J q " ( У ) sin ( k n y ) dy

• ( 1 ^{-(- 1 ) k} ) ^- W n , k

,2 2>> k п I

2 J J

+ k

' ( i -f- i y n) n ‘п ⁵

V

• J q ⁽ y ) sin ^{( kn} y ) dy ⁺ -Yn_ ( 1 ^{-(- 1 )} n ) •

• - ( - I ) * ) + W^ (1 - ( - I ) * ) + W n^ I \ ^{v 1} ) 2 k⁵ п ⁵ ’ ^{V !} ' 4

- Y JJ

fd 2 T _{+ V} d x x

a2 d2TI b2 dy2 J

sin ( n n x ) •

• sin ( k n y ) dxdy +

+ a JJ ( T - 1 ) sin ( n n x ) sin ( k n y ) dxdy 00

В результате получена замкнутая алгебраическая система линейных уравнений. Решение данной системы, его анализ и оценка погрешности будут представлены в следующей работе.