Решение задачи оптимального управления решениями одной стохастической нестационарной модели Леонтьева

Рассмотрим в R n динамическую балансовую модель экономики [1] в виде нестационарной системы

Lx (t ) = a (t ) M (t ) + f (t ) + Bu ( t ),                                 (1)

где L , M и B - квадратные матрицы порядка n , причем det L = 0 . Здесь a :[0, т ] ^ R ₊ - скалярная функция, описывающая изменение во времени параметров взаимовлияния состояний исследуемой системы, а матрица M - ( L , p ) -регулярна (т. е. существует комплексная ^^ C такая, что det( ^ L - M ) ^ 0, и ж является полюсом ( a L - M ) 1 порядка p = 0, n - 1). Вектор-функция f :[0, т ] ^ R ⁿ описывает внешние воздействия на систему, а вектор-функция и :[0, т ] ^ R ⁿ описывает управляющее воздействие на систему.

Уравнение (1) в силу условия det L = 0 нельзя разрешить относительно производной и, следовательно, при для решения таких систем не применимы классические методы решения. Системы, не разрешенные относительно производной, часто встречаются при описании экономических процессов [1] в силу невозможности запасать определенные ресурсы. Для того чтобы решить систему вида (1), необходимо выполнение некоторых специфических условий [2, 3]. На сегодняшний день подобные вырожденные системы не имеют общепринятого называния (см., например, [2–4]). В работе [4] такие системы предложено называть системами леонтьевского типа, в честь их прототипа - знаменитой балансовой модели В.В. Леонтьева «затраты - выпуск» [1]. Кроме того, такие модели часто имеют нестационарный характер, то есть входящие в них матрицы зависят от времени [5]. В данной работе будем предполагать, что зависимость от времени элементов матриц может быть некоторым образом усреднена и представлена в виде умножения матрицы при производной на некоторую функцию времени. Дополнительно отметим, что системы леонтьевского типа, являющиеся частным случаем линейных уравнений соболевского типа [6-8], вызывают большой интерес у исследователей в связи с их различными приложениями, которые находят применение не только в экономике, но и в технических системах [9, 10].

Отметим, что вырожденная система (1) разрешима не для любых начальных условий [11]. Поэтому при численных решениях для таких систем удобнее использовать начальное условие Шоуолтера-Сидорова [12]

[(v L - M )^{- 1} L ] p + ¹ ( x (0) - £ ₀ ) = 0 при v e C:det( v L - M ) ^ 0, (2) которое позволяет избавиться от необходимости согласования начальных данных. Дополнительно здесь будем полагать, что начальные условия являются случайным вектором ^ ₀ e R n .

Для решения задачи оптимального управления решениями задачи Шоуолтера - Сидорова (2) для системы леонтьевского типа (1) требуется найти функцию ui e U ad (оптимальное управление), удовлетворяющую условию

J ( u) = min J ( и );

ueUad для некоторого функционала J(и) и такое, что x(и) почти всюду на (0,т) удовлетворяет задаче (1), (2). Здесь множество Ua(i является некоторым выпуклым и компактным подмножеством допустимых управлений в пространстве управлений U . Функционал штрафа, вид которого будет приведен ниже, по сути описывает меру расхождения планируемого (наблюдаемого) поведения системы z :[0, т] ^ Z и расчетного поведения системы x(t), полученного с помощью управления и :[0,т] ^ U. Пространство Z содержит не все параметры состояния системы x(t), а только те, для которых есть информация (планируемое состояние системы).

Для систем леонтьевского типа задача оптимального управления исследовалась, например, в работах [11, 13, 14]. Задача оптимального управления решениями нестационарных систем леонтьевского типа в детерминированном случае исследована в работе [15]. Существование алгоритма решения данной задачи и сам алгоритм приведены в [16]. В силу того, что в условии (2) присутствует случайная составляющая, для решения поставленной задачи нам понадобится провести исследование в стохастическом случае [17]. Основная цель данной статьи - описать вычислительный эксперимент, иллюстрирующий результаты о разрешимости данной задачи для одной стохастической нестационарной модели Леонтьева.

Решение задачи оптимального управления

Обозначим множество матриц размера n х m символом M_{n х m} . Пусть L , M e M_{n х n} - квадратные матрицы порядка n . Следуя [7,10], будем называть множества p^L ( M ) = { pe C: det( p L - M ) ^{- 1} ^ 0 } и n L ( M ) = C \ p^L ( M ) L - резольвентным множеством и L -спектром матрицы M соответственно. Нетрудно показать [7,10], что либо p^L ( M ) = 0 , либо L -спектр матрицы M состоит из конечного числа точек. Кроме того, заметим, что множества p ^L ( M ) и n ^L ( M ) не изменяются при переходе к другим базисам. Здесь и далее будем предполагать, что p ^L ( M ) ^ 0 .

Для комплексной переменной pe C определим матричнозначные функции ( p L - M ) ^{- 1}, Rp ( M ) = ( p L - M ) ^{- 1} L и Lp ( M ) = L( p L - M ) ^{- 1} с областью определения p ^L ( M ) и будем их называть соответственно L - резольвентой, правой и левой L -резольвентами матрицы M . Также в силу результатов [7,10], L -резольвента, правая и левая L -резольвенты матрицы M голоморфны в p ^L ( M ). Ортогональные проекторы [7,10], расщепляющие пространство Rⁿ , имеют вид

P =    f Rp ( M ) d p ,    Q = -1T LLp ( M ) d p ,                    (3)

2ni2ni где контур y c C такой, что y c C и D о nL (M). Сужение матриц L и (M) на подпространства kerP и imP обозначим Lk (Mk), k = 0,1 (k = 0 для сужений на kerP и соответственно k = 1 для сужений на imP). При условии (L,p) -регулярности матрицы M (p = 0,n -1) существуют обратные матрицы L11 и M01 на сужениях пространства Rn.

Рассмотрим задачу Шоуолтера–Сидорова

P ( £ (0) - £ 0 ) = о                                      (4)

для неоднородного нестационарного стохастического уравнения

О

L £ (t ) = a (t ) M £ (t ) + B g (t ),                                (5)

где £ - производная Нельсона-Гликлиха [18], а ^ ( t ) - стохастический процесс внешнего воздействия на систему. Здесь £ (t ) = E £ ( t ) + n ( t ) и соответственно E n ( t ) = 0. Опишем пространства дифференцируемых «шумов», где данное условие выполнено автоматически и существуют производные стохастических процессов в смысле Нельсона–Гликлиха.

Пусть Q = ^Q , А ,Р) - полное вероятностное пространство с вероятностной мерой P, ассоциированное с а -алгеброй А подмножеств множества Q , а R = (R, В , ц^ - множество действительных чисел со стандартной борелевой а -алгеброй В и мерой Лебега p _L . Измеримое отображение £ : Q ^ R называется случайной величиной . Множество случайных величин с нулевым математическим ожиданием и конечной дисперсией образует гильбертово пространство L₂ = L₂(R) = { £ :E £ = 0,D( £ ) <+^ } со скалярным произведением (£ i, £ ₂) = E( £ 1 - £ ₂) и нормой I £ L = ^D £ .

Возьмем множество 3 с R , отображение п : 3 ^ L₂ задает стохастический процесс . Будем говорить, что стохастический процесс п = п ^) непрерывен на интервале 3 , если п. н. (почти наверное) все его траектории непрерывны. Множество непрерывных стохастических процессов П : 3 ^ L₂ образуют банахово пространство со стандартной sup-нормой, которое мы обозначим символом C ( 3 ;L₂). Введем в рассмотрение пространства дифференцируемых «шумов» C^£ ( 3 ;L₂) (^ е N) случайных процессов из C ( 3 ;L₂), чьи траектории п. н. дифференцируемы по Нельсону-Гликлиху [17, 18] на 3 до порядка £ включительно.

Возьмем n случайных процессов {n1(t),n2(t),•••,%(t)} и зададим n -мерный случайный про- n цесс формулой 0 = ^пj(t)ej , где ej - орты в пространстве Rn, j = 1,n . Очевидно, что п. н. все j=1

его траектории непрерывны, если пj е C(3;L2) (j = 1, n) и непрерывно дифференцируемы по Нельсону-Гликлиху до порядка t включительно, если пj е C (3;L2) для j = 1, n . По аналогии с предыдущим введем в рассмотрение пространства непрерывных C(3;L2(Rn)) и непрерывно дифференцируемых C (3;L2(Rn)) n -мерных «шумов».

Дифференцируемый процесс £(t) будем называть решением уравнения (5), если он на 3 почти наверное обращает его в тождество. Решение уравнения (5) будем называть решением задачи Шоуолтера–Сидорова (4), (5), если оно дополнительно удовлетворяет условию (4). В силу результатов [17] это решение существует для неоднородности нужной степени гладкости и имеет вид

£ (t ) = X ( t ,0) £ 0 + j x ( t , s ) I B ^ ( s ) ds - £ ( M ¹ L ) k M о¹

k = 0

\ к

1 £^ ( En - Q ) B ^ (t )

,         ()

a (t ) dt J         a ( t )

d где E – единичная матрица порядка n , символ означает производную Нельсона–Гликлиха и n                                                   dt

1                {            1

разрешающий поток операторов вида X(t,s) = -—jRL(M)exp pja(Z)dZ dp для s < t и кон- тура у с C как для проекторов в (3).

Задача (4), (5) в силу линейности эквивалентна детерминированной Lx ( t ) = a ( t ) Mx ( t ) + Bu ( t ),

\     P ( x (0) - x o ) = 0

и стохастической

₍ L n (t) = a(t)M n (t ),

^ P(П(О)-Ho) = 0

задачам. Здесь x(t) = E^(t) , n(t) = ^(t) - E^(t), x0 = E^0 , n0 = ^o — E^o . И решения этих задач можно получить с помощью (6), принимая во внимание, что производная Нельсона–Гликлиха на обычных функциях совпадает со стандартной производной. Отметим, что управляющее воздействие осталось только в детерминированной задаче (7), а стохастическая задача (8) по сути описывает влияние помех, зарегистрированных в состояниях системы в начальный момент времени.

Построим пространство H^{p + 1}( Y ) = { v g L₂((0, t ), Y ): v ^{( p + 1)} g L ₂((0, t ), Y ), p = 0, n - 1 } , которое является гильбертовым в силу гильбертовости Y со скалярным произведением p + 1 ^T /

[ v , w ] = ^[ ^ v ⁽ q ) , w ^{( q} i dt . Пусть Z - гильбертово пространство, а оператор G : X ^ Y линеен и q = 0 0

непрерывен. Построим функционал штрафа

T n                            h2

J ( u ) = J ( x (u )) = ^J Gx ⁽ q ) ( u , t ) - z ⁽ q ) ( t )   dt ,

q = 00

где G – матрица размерности n описывает выбор параметров системы, по которым будет задаваться план; вектор-функция z :[0,t] ^Z описывает планируемую динамику состояний, к которой приводят систему с помощью управления и :[0,т] ^ U (U - некоторое гильбертово пространство). Заметим, что если x g H 1(X), то z g H 1(Z). Так как U - гильбертово, то и пространство Hp+1(U) также является гильбертовым по построению. Выделим множество допустимых управлений Uad , которое является замкнутым и выпуклым подмножеством в пространстве Hp+1(U).

Вектор-функцию u g Hp+1 (U) назовем оптимальным управлением решениями задачи (7), ес- ли

J(й ) = min J ( u )                                    (10)

uGUad для функционала (9), где функции x(u) g H 1(X) и u g Uad таковы, что x(u) g H 1(X) является решением задачи (7). Существование оптимального управления решениями задачи (7) для любых z g H 1(Z) и x0 g Rn показано в [15]. В силу результатов [17] ясно, что и для задачи (4), (5) оптимальное управление существует и может быть найдено по алгоритму, описанному в [16].

Оптимальное управление решениями одной нестационарной модели Леонтьева

Рассмотрим знаменитую балансовую модель Леонтьева [1] в виде конкретной интерпретации системы (5). В этой модели матрицы L и B имеют вид

( ⁷ 20

X

. 0

X 21>

0   0

M =

-7

-4

- 11 Л

- 3

15 7

Сформулируем результат о разрешимости задачи оптимального управления решениями стохастической нестационарной модели Леонтьева.

Теорема. Пусть матрицы L, M имеют вид (11), функция a е C 1 ((0, т );R + ). Тогда для любого случайного вектора ^ ₀ е R³ существует единственное оптимальное управление задачи (4), (5), (10) с функционалом (9).

Справедливость данного утверждения следует из результатов [15, 17] в силу расщепления задачи (4), (5) на задачи (7) и (8) и с учетом того, что в [19] показано, что матрица M является ( L , 0) -регулярной.

Найдем оптимальное управление решениями задачи (4), (5). Для этого зададим

'  21 +12 C01 + C11t + C21t2 z (t) = 2 +1 - 3t2 и вид и (t) = C02 + C12 t + C22 t ,   Cij- е R, 21 +1 \          J ^ C03 + C13 t + C23 t J матрицы G = B = E3, функцию a(t) = 2t, длину отрезка оптимизации т = 2. Начальные значения возьмем в виде ^0 = (0,5а;0,3а; 0)Г, где случайная величина а равномерно распределена на отрезке [1; 2].

Для нахождения оптимальных значений подставим u (t) в (6) вместо ^( t) и для нашей моде- ли Леонтьева получим вид решения x (t)=-ИМ0) a (t)

M 01 ^ 0 + E ^ex P A t J ^{a ( Z} ) d ^Z x 0к ^ф к + \ ^eX P A t J ^{a ( Z} ) d ^Z (u ⁽ s^{) ф}к)^^-ф к

k = 1

s

где { ф ₀, ф , ф ₂ } — базисные векторы системы Леонтьева, ^ 1 = 0,2454, ^ = 2,0464 - точки относительного L -спектра матрицы M (подробнее см. в [19]). Далее это решение подставляем в функционал J ( и ) и находим его минимум по коэффициентам C ij ( i = 0,1,2; j = 1,2,3).

Используя алгоритм, описанный в [16], получим

^    5,469 + 111,74 - 1 - 102,0211 - 1 ²    '

u ( t ) =

48,3447 - 87,9749 - 1 + 102,2322 - 1 ²

₄ 42,4305 + 300,6506 - 1 + 319,5172 - 1 ² _?

Заметно, что третья компонента отличается по полученным характеристикам. Это может быть объяснено тем, что для нее взяли нулевое начальное значение.

Сравнение графиков компонент й( t ) и z ( t ) приведены на рис. 1-3.

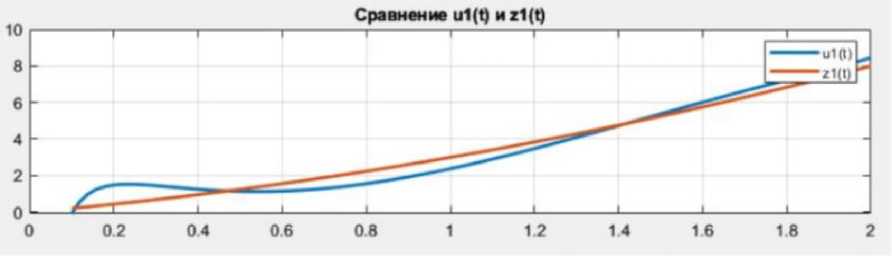
Рис. 1. Сравнение й ( t ) и z j( t ) , максимальное отклонение 0,023 при t = 1,12

и значение функционала J = J ( й) = 2,3789 . Результаты приведены в таблице.

Сводные характеристики решения

Компонента	u 1	u 2	u 3
Ji	4,7369 x 10 - 1	2,6741 x 10 - 1	1,6378
Макс. отклонение	0,023	0,019	0,031

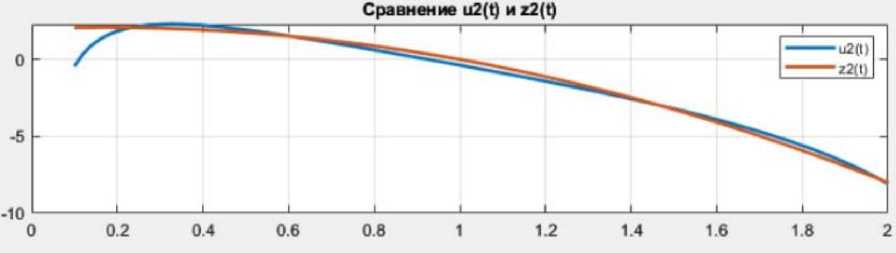
Рис. 2. Сравнение U₂ ( t ) и z ₂( t ) , максимальное отклонение 0,019 при t = 0,87

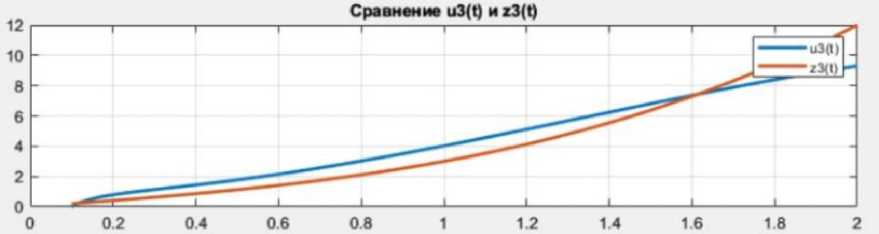
Рис. 3. Сравнение г/₃ ( t ) и z ₃( t ) , максимальное отклонение 0,031 при t = 1,45

Также вычислительные эксперименты проводились для различных значений а (рис. 4). На примере второй компоненты получили результаты, приведенные на рис. 5.

Случайный множитель rand_factor = 1.5469

Случайный множитель rand factor = 1.9575

Случайный множитель rand_f actor - 1.9649

Случайный множитель rand_factor = 1.1576

Случайный множитель rand factor = 1.9706

Рис. 4. Значение случайного сомножителя а

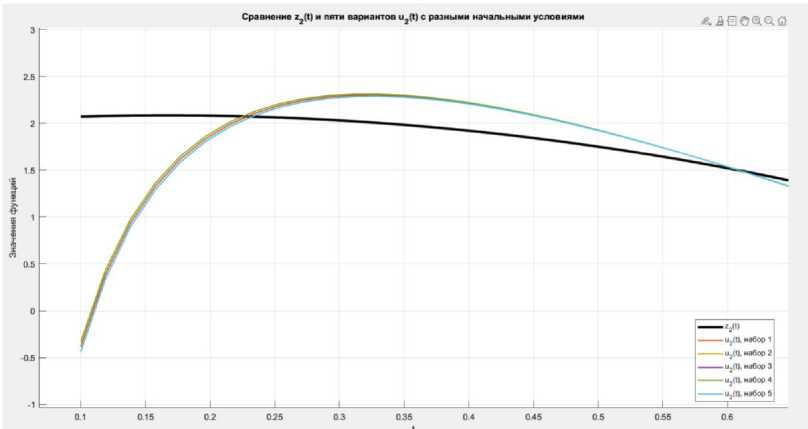
Рис. 5. Сравнение z₂ ( t ) (чёрная линия) и пяти вариантов u₂ ( t ) (разноцветные линии)

при разных начальных условиях

Заключение

В статье приведен вычислительный эксперимент для нахождения решения задачи оптимального управления решениями стохастической нестационарной модели Леонтьева. Случайная со- ставляющая предполагается в начальном условии. Результаты вычислений приведены для конкретных значений параметров модели Леонтьева в случае, когда управляющее воздействие имеет степенной вид.

Работа была частично поддержана грантом Российского научного фонда № 24-11-20037,