Решения уравнения Лапласа - Бельтрами на многообразиях с модельными концами

Введение и основные теоремы

Классическая формулировка теоремы Лиувилля утверждает, что всякая ограниченная гармоническая в Rⁿ функция является тождественной постоянной. В последнее время осуществляется следующий подход к теоремам типа Лиувилля. Пусть на римановом многообразии М задан класс функций А и эллиптический оператор L. Будем говорить, что на М выполнено обобщенное (А, Л)-лиувиллево свойство, если пространство решений уравнения Lu = 0, принадлежащих функциональному классу А, имеет конечную размерность. Оценки размерностей различных пространств решений эллиптических уравнений на некомпактных римановых многообразиях были получены в работах ряда математиков ^].

В данной работе в качестве эллиптического оператора L рассматривается оператор Лапласа — Бельтрами А и, соответственно, рассматриваются гармонические функции.

Ряд работ был посвящен изучению гармонических функций на многообразиях с концами. Пусть М — полное некомпактное риманово многообразие и В С М — компактное множество. Связную неограниченную компоненту Е С М \ В такую, что ЭЕ — компакт, будем называть концом М по отношению к В. Если число концов М относительно некоторого компактного множества равномерно ограничено сверху целым числом, то говорят, что М имеет конечное число концов. В этом случае существует положительное R и целое k > 1 такие, что если Q — некоторая ограниченная область, содержащая B0(R\ то М \ Q имеет ровно к неограниченных компонент. Здесь В0(Н) — геодезический шар радиуса R с центром в точке о Е М. Различают концы параболического и гиперболического (или непараболического) типа. Конец называется концом параболического типа, если его емкостный потенциал равен тождественно константе, и гиперболи-9 ческого типа в противном случае .

Во многих работах рассматривались различные пространства гармони- ческих функций на многообразиях с концами. Так, в 3 было доказано, что если многообразие М имеет т концов, то т < dimH^Af); более того, если М имеет гиперболический тип, то т < dimH+(M),' где W(M) — пространство гармонических на М функций, которые ограничены либо сверху, либо снизу на каждом конце, Н+(М) — пространство неотрицательных гармонических на М функций. Там же было показано, что если М имеет неотрицательную кривизну Риччи, то dimH^AT) = dimH+(Af) = т.

В данной работе рассматриваются многообразия с модельными концами. Пусть полное риманово многообразие М представимо в следующем виде:

М = В U Di U D2 U и Dmi где В — некоторый компакт, а компоненты связности Di изометричны прямому произведению [го, +оо) х Si с метриками ds2 = d^A-Pi^dO2. Здесь Si — компактные римановы многообразия без края, дг(г) — положительные гладкие на [го, +ос) функции, d6; — метрика на Si- Компоненты связности Di будем называть концами многообразия М по отношению к компакту В.

. . Будем рассматривать гармонические функции на описанных многообразиях,

Введем обозначения:

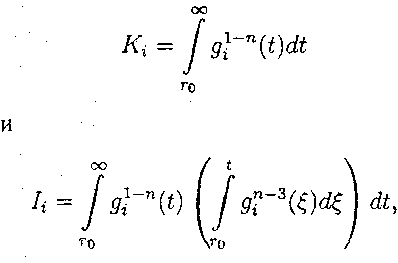
где п = dim М. "

Замечание. Конец Di имеет гиперболический тип тогда и только тогда, когда Ki < сю.

Доказательство легко получается из того, что функция

Т

^т) = j g-^^dt ГО является емкостным потенциалом конца

Несложно показать, что на каждом конце Di выполнено в точности оДно из условий:

• 1)    Кг = ОО.

• 2)    Ki < оо, Ц = оо. Будем говорить, что такой конец Di имеет слабо гиперболический тип.

• 3)    Ц < оо. Будем говорить, что такой конец Di имеет строго гиперболический тип.

Определение 1. Пределом функции и по концу Di назовем число

ЬтиСг.ОЛ = lim u(r. 9Л, если последний предел существует и не зависит от 9i.

Определение 2. Потоком гармонической функции и по концу Di назовем число flux и =    /    -д-du,,

Di        J    Ov

DiOdBo^ где v - единичная внешняя нормаль к ЭВо(т\                          .

Заметим, что в силу формулы Грина величина потока не зависит от г.

Ранее А.Г. Лосевым в работе 5 были даны точные оценки размерностей пространства ограниченных и конуса положительных гармонических функций на указанных многообразиях.

Целью данной работы является оценка размерности пространства Н'(М) и доказательство разрешимости некоторых краевых задач для функций -и е н\м\

Справедливо следующее утверждение.

Теорема 1. Пусть на многообразии М s концов Di, г = l,...,s имеют параболический тип., I концов Dj, j = s + l,...,s + I имеют слабо гиперболический тип и р концов Dk, k = s + Z +1,..., s + l+р имеют строго гиперболический тип, причем 1ц-р > 1. Тогда для любого набора ^0^,02, ...,a_s, bs+h ^s+2: •■•, ^s+Z, Ф₅₊/₊1,...,Ф_5+;+р), где axi-.^Os, b_s+i, ...,b_s+i — произвольные константы, а Ф_к = Ф&№) — непрерывные на S_k функции, существует единственная функция и Е Н^М) такая, что

Н их и = at, г = 1,..., s;

limit = bj, j = s + 1,..., s + Z;

lira ^7,9^ = Ф^(^), r—^oo^kESk

A; = s + Z + l,...,s + Z + p.

Аналогичное утверждение для функций и Е H⁺(Af) было доказано в работе ⁶.

Используя доказательство теоремы 1, несложно получить следующее утверждение.

Теорема 2. Пусть многообразие М имеет s концов параболического типа и Z > 1 концов слабо гиперболического типа и не имеет концов строго гиперболического типа. Тогда dimS^ — s-Vl.

Таким образом, учитывая работу 7, на многообразиях с модельными концами справедлива оценка dimH^M) = dimH+(M) = s + I.

1.    Вспомогательные утверждения

Переобозначим для фиксированного г Di через D и Si через S.

Лемма 1. 5 Пусть Q — пред-компактное открытое множество в М, граница dSl которого состоит из непересекающихся компактных гиперповерхностей Fi и /ф. Пусть и — гармоническая функция в Q, непрерывная в Q, причем ul^ < 0, и|^2 > 0. Тогда

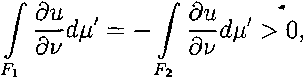
где и — единичная внутренняя нормаль.

Лемма 2. Пусть и Е №(M). Пусть D С М — некоторый конец многообразия М. Тогда fluxu(r, 0) = gn 1

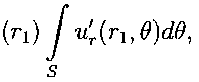
где Ту > т — произвольное фиксированное число.

Доказательство. Непосредственно из определения имеем flux it =        —-du =

Di        J ди

DiC\8Bo^

= j ^С^д-'ЮМ =

s

= у u'_r(r,9)gⁿ ^^dO = s

= 9n~4r) jи'Лт.9^9, s что и требовалось показать.

Лемма 3. Пусть и 6 H7(M). Пусть D С М — конец слабо гиперболического типа. Тогда существует конечный предел lira и(г, в), т—'Оо^т.Э^ЕП не зависящий от 6.

Доказательство. Поскольку и Е Н^ЛГ), то функция ц(г, 0) ограничена либо сверху, либо снизу на D. Пусть и ограничена сверху на D константой N. Тогда функция

f(r,9) = N — Цг, 9)

является гармонической и положительной на D. Как показано в 9, существует конечный предел lim / на D,

Т—*ОО не зависящий от 9. Учитывая, что u(r,0) = N — f^r^GY получаем требуемое.

Доказательство в случае, когда и ограничена снизу на D, аналогично.

2.    Доказательство теоремы 1

Построим функцию и(т) Е H^Af) такую, что flux и = аг, г = 1,.... s; Di

\imu = bj, j = s + 1,...,s + I;

и покажем, что она будет единственной для набора ai, .... a_s, b_s+1, .... b_s+i, Фе-Н+Ь •••> Фз+i+p-

Рассмотрим непрерывные функции Ф^(0^), fc = s + Z + l,...,s + Z + p. Т. к.

9_k Е Sk, a Sk — компактное многообразие, то существует           ., т; _;

L= min min Ф_к(9_к^ (1)

к —s-bZ4-l,...,s-|-Z+p @k^S_k

Рассмотрим новый набор функций

®ж)=^ш - д k = S-\-lA*A.)...,SA-l"V"P-

Очевидно, что Ф^№) являются неотрицательными непрерывными функциями на Sk. В 10 показано, что на М существует единственная положительная гармоническая функция и'^ такая, что ее потоки по концам параболического типа, как и пределы по концам слабо гиперболического типа равны нулю и lim ^А) = Ф'кМ r—»oo,0kGSk fc = s + Z + l,...,s + Z+p.

Введем следующие обозначения:

• 1)    Если г = 1,..., s, то положительную гармоническую на М функцию, поток которой по концу параболического типа Di равен 1, а потоки по остальным концам параболического типа, как и пределы по всем концам гиперболического типа равны нулю, будем обозначать через fD_t.

• 2)    Для j = s + 1,..., 8 + Z через hoj будем обозначать положительную гармоническую на М функцию, потоки которой по всем концам параболического типа равны нулю, предел по концу слабо гиперболического типа Di равен 1, а остальные пределы по всем концам гиперболического типа равны нулю.

Заметим, что существование положительных гармонических функций /щ, -., Ь„ Vt_Ds+v .... h_{D L} доказано в ^п ......

Построим на М функцию и" € Н^М) такую, что ее потоки по концам параболического типа равны а_г,...,а₈, ее пределы по концам слабо гиперболического типа равны b'_s+y, ...,b'_s+t и ее пределы по концам строго гиперболического типа равны нулю. Здесь У₈₊₁ = b_s+t — L, ..., b'_s+i = Ь₈_ц — L, константа L определяется по формуле (1).

Очевидно, что этим условиям удовлетворяет функция .

• -- s                      s+Z ■          ■

11" = ^а_гЬ_г + ^ ^bjh_Dj G W.

1=1              j=s + l . . ■ -

Покажем, что построенная функция и" G Н^М) будет единственной на М.

Пусть «1 G Н'(М) и «2 € Н'(М) такие функции, для которых наборы (ai,...,a_s, ^₊₁,..., b'_s+l) совпадают и пределы по концам строго гиперболического типа равны нулю. Рассмотрим функцию

ы* = «1 — «2-

Очевидно, что и* Е W(M) и ее потоки по всем концам параболического типа, как и пределы по всем концам гиперболического типа, равны нулю. Покажем, что и* = 0,      .       .

откуда будет следовать единственность.

Пусть Di — конец параболического типа. Функция и*(г, 6) ограничена либо сверху, либо снизу на D^ Пусть ц*(г, 9) ограничена сверху константой N на Di. Рассмотрим функцию

/(т) = N - и* (ж).

Очевидно, что функция / является неотрицательной гармонической на D.;

функцией, причем ее поток по концу Di равен нулю. Тогда, как показано в ¹², существует конечный предел функции / по концу Di. Отсюда следует существование конечного предела функции и* по концу Di. В случае, когда функция и* ограничена снизу на О_г, аналогично можно показать, что существует конечный предел и* по концу Di.

Положим

Pi = lim u*(r,9i), г = 1,.... s + Z + p г—»oo,dj€Sj

И

Р = min Pi.

T. к. пределы функции и* по концам гиперболического типа равны нулю, то pj = 0 для всех j = s +1,..., s + l+p.

Предположим, что р < 0. Пусть I — набор индексов таких, что Jim^w* = р. Тогда существует такое г > 0, что р < —е < pi, г£ I.

Рассмотрим функцию у = и* + е.

Заметим, что flux у = flux и* = 0 для Dt        Dt всех г = l,...,s. Рассмотрим при достаточно больших г область, ограниченную всеми сечениями Di^ — Di П дВог, г = 1,..., s + Z +р. Тогда y^^ln^r),^/ < 0, p(r,6*)|Di(r)ji^ > 0, откуда из леммы 1 следует, что

• —52 ^^их у > iei ¹

что противоречит условию flux^ р = 0 V? = 1, ..., 8.

Таким образом, предположение о том, что р < 0 не верно, откуда в силу принципа максимума функция и* неотрицательна на М. Аналогично можно показать, что

Р = max Pi < О, г=1,...,$ откуда в силу принципа максимума функция и* неположительна на М.

Окончательно получаем, что и* = 0 на М.

Единственность функции ц"(ж) на М показана.

Таким образом, мы построили на М две функции и'(ж) 6 Н^М), и"(х) G Н^М) такие, что flux и' = О, г = 1,s;

Di

Umi? = 0, у = s + 17..., s + Z;

lim  и'(г А) = Ф'^),

. r^oo,9k£Sk к — s + Z + 1,..., s + I А- р

и йихи" = а7, г = 1,...,з;

limu" = Р, 7 = s + 1,.... s + 1л lim ti"(r10k) = 0, r^oa,9keSk

• к = s + Z + l,...,s + Z + p,

где Ф'^) = Ф_к A) - L, b' = b, - L,

L = min min Фк(6к\ Кроме ; ' •   А1=бЧ-/+1;...,54-Л-Р ^k^Sk того, показано, что функции ц'(ж) и «"(ж) являются единственными на М.

Рассмотрим функцию

ц(ж) = и\х) + и" (ж) + L.

Очевидно, что и(ж) € Н^М) и flux и = г = s;

D.

lim u = bj, j = s + 1, ...,s + Z;

Dj lim u(r, 0k) = ФаА), T—tOGjUk^Sk k = sAl + i,...,sAl"bp-

Кроме того, функция и(ж) является единственной для набора aj, .... as, bs+i, .... bs+l, Ф5+<+1..... Ф5+/+Р в силу единственности функций и^ж) и ^"(ж).

Теорема 1 полностью доказана.

3. Доказательство теоремы 2

Пусть многообразие М не содержит концов строго гиперболического типа. Пусть, как и ранее, Di,..., D_s — концы параболического типа, D_s+1,..., D_s+i — концы слабо гиперболического типа, Z > 1.

Несложно проверить, что положительные гармонические функции f_Dv .... fn_a, h,_Ds+v .... hD_3+l линейно независимы.

Пусть и 6 Н^М). Из леммы 3 следует, что на концах Ds+i,..., Ds+i существуют конечные пределы функции и, не зависящие от 0j, j = s + 1,..., s + Z. Пусть bs+i,..., bs+i — набор этих пределов. Пусть также ац,...,^ — потоки функции и по концам параболического типа Di,..., Ds. Рассмотрим функцию s              s+Z и -г? u djjpi          bjh-Dj.

1=1         J=s+1

Очевидно, что и* € Н^М) и ее потоки по всем концам параболического типа, как и пределы по всем концам слабо гиперболического типа, равны нулю. Как и при доказательстве теоремы 1 несложно показать, что и* = 0, откуда s             s+Z ц = ^2adD1 + Ьз1гпз' г=1         j=s+l

• т. е. набор /_Д1, .... f_Ds, h_Ds+v ..., hn^ является базисом пространства Н'(М).

Отсюда окончательно получаем, что dimH^M) = s + I.

Теорема 2 доказана.