Решения в скалярно-торсионной теории гравитации для степенной эволюции скалярного поля

В настоящей работе рассматривается обобщенная скалярно-торсионная теория F(Т, 。 ) = F (0)Т гравитации, где F ( 。 ) представляет произ вольную функцию, Т — скаляр кручения. Ключем к нахождению верифицируемых по наблюдательным данным решений является выбор неминимальной связи между функцией скалярного поля F ( 。 ) и скаляром кручения вида F 〜 Т^п/2, г де п

Настоящая работа выполнена в рамках Дополнительного соглашения №073-03-2024-060/1 от 13.02.2024 к Соглашению о предоставлении субсидии из федерального бюджета на финансовое обеспечение выполнения государственного задания на оказание государственных услуг (выполнения работ) № 073-03-2024-060 от 18.01.2024, заключенным между ФГБОУ ВО «УлГПУ им. И.Н. Ульянова» и Министерством просвещения Российской Федерации.

• ¹    E-mail: bolshakova.ktrn@gmail.com

• ²E-mail: chervon.sergey@gmail.com

• ³E-mail: ingvor@inbox.ru

произвольная постоянная. Записанные уравнения космологической динамики допускают возможность вычисления параметра Хаббла в случае степенной зависимости скалярного поля от времени и провести согласование параметров модели с ограничениями по наблюдательным данным.

1.    Общие уравнения

Мы рассматриваем обобщенную скалярно-торсионную гравитацию [1] с действием вида:

S = / d4,e 卜；F(0)7 -乎32 + V(°)].

Здесь F, ®, V произвольные функции скалярного поля 0, точка над функцией означает производную по времени, 7 — скаляр кручения, е = det[e^] =， -g.

Выбираем тетраду для однородной и изотропной фоновой геометрии:

寸=diag {(a⑴,a⑴,a⑴} , которая соответствует метрике Фридмана-Робертсона-Уокера:

ds2 = —d力2 + a2% dx^dx^.

Здесь a (。一 масштабный фактор, зависящий от космического времени t. Поскольку диагональная тетрада в декартовых координатах (2) является собственной тетрадой, спиновая связность обращается в ноль: ® 氤= 0.

Уравнения космологической динамики выводятся при варьировании действия (1) по тетраде

• [1] . В полученные уравнения мы подставляем функцию неминимального взаимодействия, следуя

  [2], вида: F(0(t))=( 噂 ) ,где космологической динамики:

  
  

А > 0, п = const. Таким образом, мы имеем следующие уравнения

九/

V = 巧( 3Н² + А(1 + n)),

⑷

30 ²

—2 (£) H(n +1),

⑸

где з(0) - произвольная функция. Отметим, что данные уравнения получены в работах [2,3], где з = const. В настоящей работе мы полагаем з(0) = ±1 = з*, что отличает наш подход от предыдущего.

2.    Формулы для расчета космологических параметров данной модели

Космологические возмущения влияют на анизотропию и поляризацию реликтового излучения. Благодаря этому, есть возможность произвести оценку инфляционных моделей по наблюдательным данным. По последним данным, полученным в работе [4] ограничения на параметры космологических возмущений имеют следующие значения:

Vs = 2,1 X 10^-9, г< 0,032, n_s — 1 = 0,9663 ± 0, 0041.

⑹

Для нашей модели космологические заданной неминимальной связи F = возмущений:

параметры будут рассчитываться по формулам [2] с учетом

(*"

Формула для расчета спектра мощности скалярных

А^ 2(n + 1)е

(Ž )2

⑺

Спектральный индекс скалярных возмущений:

ns — 1 = (n — 4) е + 28 .

⑻

Отношение тензорного спектра мощности к скалярному (тензорно-скалярное отношение):

От г = — = 16(п + 1)е .                                  (9)

Формулы для расчета параметров медленного скатывания:

е =	Н   1 一 Н2 京 1 ,	(10)
8 =	•• « 1. 2НН	(11)

2.1.    Инфляционные решения для степенного скалярного поля.

Рассмотрим степенную эволюцию скалярного поля вида ф = 。力卜 г де D, к = const.

Из уравнения (5) находим параметр Хаббла:

• - Щк、，

здесь С — константа ііптегрііроваіііія. Масштабыый (фактор находим в пу ) с¹ дположс¹! 11 ii і С = 0 ： i

/ 2：+一、        I"—®*MD2k2] a1 (n +1)..

а =。0 ехР (，，石=IT] Е'^)

Так как подкоренное выражение в Н должно быть больше ноля, при С = 0 имеем две возможности i) ®* = 1, к < 1/2 и ii) ®* = —1, к > 1/2. Выбираем второй вариант, так как в первом случае не возможно согласование по наблюдательным данным.

Потенциал V (ф) ⑷ с учетом параметра Хаббла (12) при С = 0 принимает вид:

V (ф)

3*MD2 k2

2(2k — 1)

2 к -1 -i (г

九 + 2 ^ +1

2(к-1)

23*^D2k2 ( D )

.

Запишем значения параметра Хаббла и его производных для дальнейших вычислений при к = 3/4 ：

Н

А_п = k²AⁿD²

下炉， ^{h (t)}=^A-…А

2(n + 1)

1   — 2 - +1

A”t-25 + ¹ )

•• Н

2n + 1 4(n + 1)2

AL¹ 厂

4 九 + 3 2( " + 1)

Параметры медленного скатывания (10) и (11) для данной модели при к = 3/4 таковы:

е

2(n +1)

_— 1

AJ+11—

2 九 + 3 2( ^ +1)

(1 + 2n) 4 (n + 1)

— ¹     2 ^ +3

A 」 ¹1^— 2^+П.

Учитывая (12) при С = 0, находим число е-фолдов:

N =22^ 12^ A 卢

.

Полагая N = 60. находим время пересечения горизонта t*

³⁰⁽²ⁿ + ^{3)  —} ^ +1

一 (n +1) ^An

2( 〃 + 1)

2 ^ + 3

.

Тогда параметры медленного скатывания:

1,

€* = ,

*      60(2п + 3)，

6* =   1+：：

120 (2 : + 3)

Отметим здесь, что в нашем случае, при 乂 * = —1, условие Н >  0, что соответствует суперинфляции [5,6], выполняется при : < —1.

Для расчета спектра мощности скалярных возмущений мы находим значение параметра Хаббла при пересечении горизонта:

i

Н* = 簿畳[ 3^ 厂.              ( 23)

Расчет космологических параметров при пересечении горизонта для данной модели по формулам (7), (8) и (9) дает:

人("方 * )=- 5 ▲— l³⁰^)

4тт²          I (: + 1) 丿

_       (:+ 5)

$    — 60(2: + 3),

• 4 (: + 1)

r =--

15(2 : + 3) ・

Исходя из полученных формул (25) и (26) зависимость г = г(:$) такова:

16 ( : $ — 1) ( : + 1) : + 5

Проводя анализ данной формулы находим следующие ограничения на значения для : и для показателя степени скалярного поля к = 3 / 4: — 1 . 087 < : < — 1 . 010. Проводя анализ (24) при 乂 * = — 1 получаем ограничение на амплитуду скалярного поля D и Л: D⁹-⁶⁸⁵^⁴-¹⁷⁷ ~ 1.616 义 10^-15.

0 20

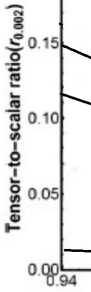
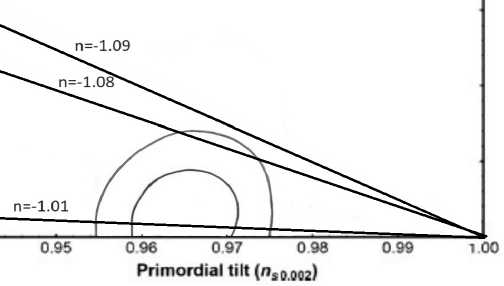
Рис. 1. Зависимость 丁 = r(n_s) пр и к = 3/4 для разных значений параметра п = -1.09, -1.08, —1.01.

Заключение

Используя функционально-параметрическую связь между функцией неминимального взаимодействия и кручения вида F 〜Т"/2, предложенного в работе [2], найдено семейство решений для скалярного поля, эволюционирующего по степенному закону. Среди полученных решений найдены те, которые согласованы по наблюдательным ограничениям. Выбранные параметры модели приводят к необходимости фантомизации скалярного поля. Показано, что для всех моделей со степенью эволюции скалярного поля к при к > 1/2 наличие неминимальной связи позволяет верифицировать модели космологической инфляции, используя наблюдательные ограничения на параметры космологических возмущений.