Решеточный метод Больцмана в задачах кондуктивного теплопереноса с учетом химических реакций в материале

Решеточный метод Больцмана (Lattice Boltzmann method или LBM) является относительно новым инструментом для решения задач газовой динамики и тепломассопереноса [1–4]. Ядром этого метода является решеточное уравнение Больцмана, которое представляет собой особую форму кинетического уравнения Больцмана, дискретизированного по пространству и времени. LBM можно рассматривать как подход статистической физики, существенно отличающийся от «традиционных» макроско- Для цитирования

пических методов механики сплошной среды, которые обычно применяются при моделировании процессов химической инженерии.

В рамках решеточного метода Больцмана анализируется микродинамика условных частиц с помощью упрощенных кинетических моделей. Кинетическая природа привносит многие отличительные особенности LBM от «традиционных» численных методов, такие как простота численной реализации и естественный параллелизм. Во многом эти особенности и привлекают исследователей к использованию LBM.

This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International License

Следует отметить, что рассматриваемый метод преимущественно используется для решения задач гидрогазодинамики [5, 6]. В этой связи, представляет интерес оценка возможности применения LBM для анализа процесса теплопроводности в твердом материале с учетом химической реакции. Таким образом, целью настоящей работы является математическое моделирование процесса кондуктивного теп-лопереноса мезоскопическим решеточным методом Больцмана.

Материалы и методы

Рассматривается краевая задача пространственного кондуктивного теплопереноса. Область решения представлена в виде, например, полимерного материала кубической формы (рисунок 1).

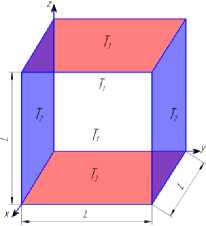
Рисунок 1. Область решения

Figure 1. Solution domain

Предполагается, что теплофизические свойства материала не зависят от температуры. На границах задаются краевые условия первого рода. Макроскопическое уравнение теплопроводности для рассматриваемого случая имеет следующий вид:

д T     ( д2 T  д2 T  д2 T )

= a "I        ++I +, д t      ( дx2   дy2   дz2 J  c• p где T – температура, К; t – время, с; a – коэффициент температуропроводности,м

• x, y, z – декартовы координаты, м;

=    .....

9v хим» 0 P P^ r " t J —         объемный источник выделения или поглощения теплоты за счет химической реакции, Вт/м3; с – удельная изобарная теплоемкость, Дж /(кг" К);

ρ – плотность, кг/м³.

Уравнение (1) замыкается следующими начальными и граничными условиями:

t = 0: T ( x , y , z ,0 ) = T _o,           (2)

t >  0, x = 0, 0 <  y <  L , 0 <  z <  L : T = T ,  (3)

t >  0, x = 1,0 <  y <  L , 0 <  z <  L : T = T , (4) t >  0, y = 0, 0 <  x <  L , 0 <  z <  L : T = T ₂, (5)

t >  0, y = 1, 0 <  x <  L , 0 <  z <  L : T = T ₂, (6)

t >  0, z = 0, 0 <  x <  L , 0 <  y <  L : T = T ₃, (7)

t >  0, z = 1,0 <  x <  L , 0 <  y <  L : T = T ₃. (8)

Рассматриваемый процесс можно также описать при помощи кинетического уравнения Больцмана вида:

^^ + u "V f =Q , д t

где f – функция распределения, кг/м3; Ω – интеграл столкновения, кг / (с^м3); u – вектор скорости, м/с.

Применяя трехмерную семискоростную схему (рисунок 2) и BGK аппроксимацию, получим решеточные уравнения Больцмана:

^ f k- + u "V f , = _m ( f eq - f .) + s , , (10)

где – равновесная функция распределения, кг/м3; = ⋅⋅ – источниковый член, кг / (с^м3); ω – частота релаксации, 1/с; k = 1.7.

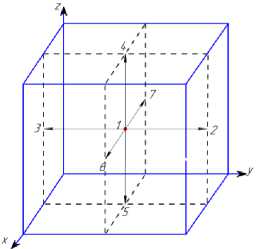
Рисунок 2. Схема D3Q7

Figure 2. D3Q7 scheme

Уравнение (10) может быть дискретизировано как:

f , ( ^{x +} c , " ^A t , t ^+A t ) =

= f , ( ^x , t ) ^{+ A} t " ® "[ req ( ^x , t )^- f , ( ^x , t ) ] ^{+ A} t " S , .⁽¹¹⁾

Равновесная функция распределения для D3Q7 схемы рассчитается как:

f eq = Wk " p "

^{1 + 3} " ( c ,• u )^{+ 9} " ( c ,• u ) ² - ³ " ( u " u ) ,

Поскольку рассматривается процесс теплопроводности, вектор скорости равен нулю. В этом случае равновесная функция распределения принимает частный вид:

f eq = w , " t .           (13)

Весовые коэффициенты w и скорости частиц для схемы D3Q7 имеют следующие значения:

w

= 4;

_ 8;

к = 1, к = 2..7.

Согласно теории Чепмена–Энскога температура восстанавливается из функции распределения следующим образом:

T ( x , t ) = £ f_k ( x , t ) .           (14)

k = 1

• •    Восстанавливается макроскопическая температура из мезоскопической функции распределения.

• •    Шаги 2 - 7 повторяются до достижения заданного количества итераций.

Частота релаксации рассчитывалась как:                   ^{Результаты и обсуждение}

ю =

a     Г ’

+— cs2 -At   2

где сs – скорость звука в узлах решетки, м/с

На границах задаются следующие условия для функции распределения:

t > 0, x = 0, 0 < y < L , 0 <  z < L : f 7 = T ( w 6 + w ₇ ) - f 6 , (16)

Математическое моделирование процесса кондуктивного теплопереноса проведено при варьировании объёмного источника выделения и поглощения теплоты. Для удобства анализа экзотермических и эндотермических реакций q v будет задаваться, а не рассчитываться. Значения входных параметров приведены в таблице 1.

Таблица 1.

t >  0, x = 1, 0 <  y <  L , 0 <  z

t >  0, y = 0, 0 <  x <  L , 0 <  z

< ^L : f 6 = ^T1 ^{( w} 6 ^{+ w} 7 ^)- f 7 , (17)

Входные данные

< ^L : f 2 = ^T 2 ( w 2 ⁺ w 3 ) - f 3 , (18)

t >  0, y = 1, 0 <  x <  L , 0 <  z <  L : f = T₂

^{( w}2 ⁺ w , ^)- f , , (19)

t >  0, z = 0, 0 <  x <  L , 0 <  y <  L : f₅ = T₃

⁽ w 4 ⁺ w 5 ^{)- f} 4 , (20)

t >  0, z = 1, 0 <  x <  L , 0 <  y <  L : f. = T ( w. + w, ) - f, 4   34   5    5

Упрощенный алгоритм решения краевой

задачи при использовании решеточного метода Больцмана состоит из следующих частей:

• •    Задаются начальные параметры.

• •    Начало итерационного цикла.

• •    Рассчитываются равновесная функция распределения и теплота химической реакции.

Table 1.

Input data

L	0,1
а	6,22 ×10-7
C	750
ρ	1500
Т0	298
Т1	283
Т2	273
Т3	323
qv	104; 105; -104; -105

На рисунке 3 приведены поля температур в динамике. Как и можно было предположить,

• •    Процедура “Collision” в LBM.

• •    Процедура “Streaming” в LBM.

• •    Рассчитывается функция распределения на границах полости.

температура в ядре материала увеличивается в условиях экзотермической реакции и понижается при учете эндотермической с течением времени.

(b)                                               (c)

(a)

(d)                                              (e)                                                   (f)

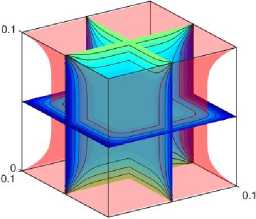
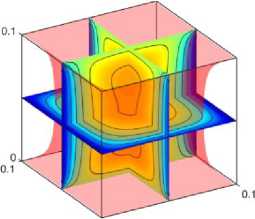
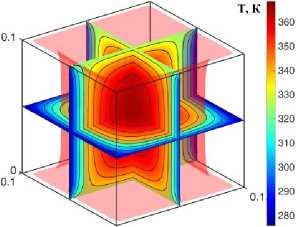
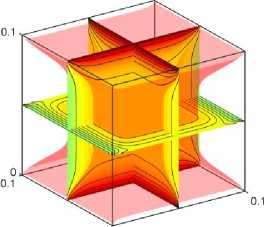
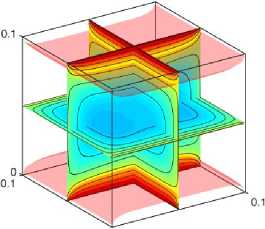
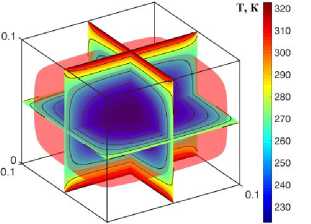
Рисунок 3. Поля температур с учетом экзотермической q_v = 10⁵ (a , b, c ) и эндотермической q_v = -10⁵ ( d, e, f ) реакций при: (a) , (d) t = 100; (b), (e) t = 500; (c), (f) t = 1000

Figure 3. Temperature fields taking into account exothermic q_v = 10⁵ (a, b, c) and endothermic q_v = -10⁵ (d, e, f) reactions at: (a) , (d) t = 100; (b), (e) t = 500; (c), (f) t = 1000

Установлено, что при t = 100 тепловой эффект эндотермической реакции незначителен. Как результат, значение температуры в ядре практически равно начальной и перенос энергии осуществляется только у границ материала. С другой стороны, температура в центре области решения увеличивается примерно на 10 К при рассмотрении экзотермической реакции. С увеличением времени до 500 распределение температур в окрестности нижней и верхней границ изменяется несущественно, в то время как происходит модификация изотерм у других стенок материала при эндотермической реакции. При этом противоположные закономерности теплопереноса можно также выделить в условиях экзотермической реакции. Аналогичные паттерны наблюдаются и при дальнейшем увеличении времени. Для оценки достоверности результатов численного моделирования рассматриваемая краевая задача также решена традиционным методом конечных разностей (FDM). Поскольку решеточный метод Больцмана является явным, дифференциальные уравнения второго порядка в частных производных аппроксимировались явными конечно-разностными схемами. Для временной производной использовалась схема Эйлера, а для диффузионных слагаемых - центральные разности второго порядка точности по пространству.

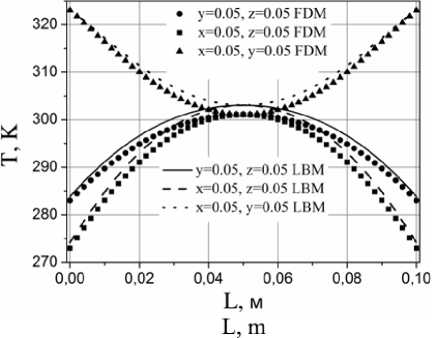
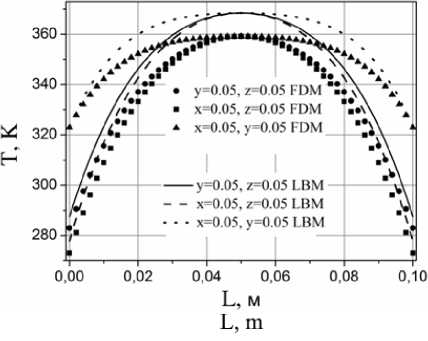
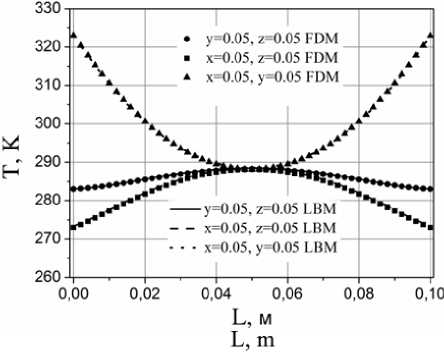
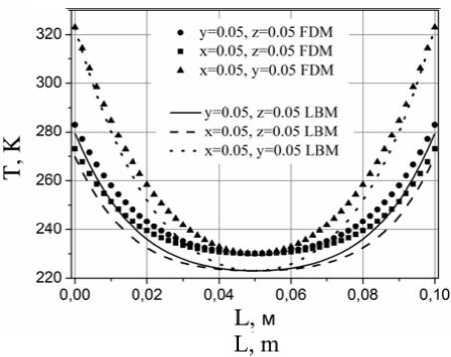
На рисунок 4 приведены распределения температур в характерных сечениях. На основании анализа представленных на рисунок 4 данных можно сделать вывод, что решеточный метод Больцмана адекватно воспроизводит рассматриваемые характеристики теплоперено-са. При этом интересно отметить, что наилучшее совпадение результатов достигается в условиях эндотермических реакций. Во всех рассмотренных случаях LBM дает корректные профили температуры, а отклонения локальных значений лежат в пределах 5 %. Такая погрешность может быть обусловлена неявной конвертацией макроскопических граничных условий первого рода посредством мезоскопической функции распределения.

(a)

(b)

(c)

(d)

Рисунок 4. Распределения температур при: (a) q_v = 10⁴; (b) q_v = 10⁵; (c) q_v = -10⁴; (d) q_v = -10⁵

Figure 4. Distribution of temperatures at: (a) q_v = 10⁴; (b) q_v = 10⁵; (c) q_v = -10⁴; (d) q_v = -10⁵

Хорошо видно, что изотермические условия выполняются с ошибкой при LBM. Одним из вариантов решения этой проблемы представляется принудительное задание параметров на стенках материала после шага восстановления температуры из функции распределения. Также следует отметить, что решеточный метод Больцмана воспроизводит большие / меньшие значения температуры в условиях экзотермических / эндотермических реакций. Возможно, понижение частоты релаксации приведет к лучшему согласованию результатов численного моделирования. Известно, что при решении задач гидрогазодинамики LBM имеет преимущество перед традиционными численными методами в скорости расчета программы. В этой связи, представляет интерес оценка вычислительной производительности решеточного метода Больцмана при моделировании процесса теплопроводности.

На рисунке 5 представлены времена исполнения программ при варьировании количества узлов расчетной сетки.

На основании сравнительного анализа установлено, что решеточный метод Больцмана существенно проигрывает традиционному методу конечных разностей при количестве узлов ≥ 613.

Однако, такой результат в некотором смысле предсказуем, поскольку при решении задач теплопроводности отсутствует необходимость решать стационарные уравнение неразрывности потока и Пуассона для поля давления на каждом шаге по времени как в случае численного анализа процессов газовой динамики. Более того, при использовании трехмерной семискоростной схемы решается семь уравнений для функции распределения, в то время как при применении классического метода конечных разностей – одно уравнение энергии.

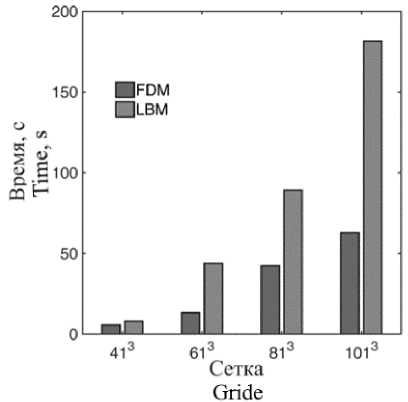
Рисунок 5. Время расчета программ при t = 1000 Figure 5. Time of calculation of programs at t = 1000

Заключение

Численно проанализирован пространственный процесс кондуктивного теплопереноса в полимерном материале с учетом экзотермических и эндотермических реакций. По результатам проведенных исследований установлено, что относительно новый решеточный метод Больцмана корректно воспроизводит поля температур. Однако при решении задач теплопроводности LВМ уступает в скорости расчета традиционным численным методам. Дальнейшие направления исследований могут включать постановку нелинейных граничных условий и учет термического разложения материала.

Исследование выполнено при финансовой поддержке Российского научного фонда № 21–79– 00011.