Ресурс несущей способности традиционных и предварительно напряженных биметаллических балок, при пластической работе материала их стенки

Известно, что во всех металлических конструкциях в период их изготовления возникают пластические деформации, вызванные их сваркой, болтовыми или заклепочными соединениями. Многочисленные работы академиков Е. О. Патона [1], Н. Н. Давиденкова [2], профессоров В. П. Вологдина [3, 4], Н. А. Гликмана [5, 6], П. И. Кудрявцева [7, 8], Г. А. Николаева [9, 10], Н. С. Окерблома [11, 12] и других убедительно раскрывают физические процессы при сварке металлов.

В процессе эксплуатации металлические конструкции, прежде всего балки, находятся под воздействием различных нагрузок, которые вызывают в них разнообразное напряженное состояние, иногда сопровождающееся пластическими деформациями. Исследованию влияния пластических деформации на хрупкость и вязкость стали, выносливость конструкций, их хладноломкость и коррозионную стойкость, напряженно-деформированное состояние при статических, динамических и сейсмических нагрузках посвящено большое количество научных исследований.

Методы теории вероятностей и теории надежности в расчетах сооружений изложены в фундаментальных работах В. В. Болотина [13], Г. Нейбера [20], А. Р. Ржаницина [21], А. Г. Ройтмана [22], сопротивлению элементов конструкций хрупкому разрушению посвящена работа [14], работа стальных металлических балок при низких температурах освещена в монографиях [15, 16], хрупкие разрушения сварных конструкций изложены в работе [17], механике хрупкого разрушения посвящена работа [18], практические приемы определения коэффициентов концентрации в металлических конструкциях сформулированы в монографии [19]. ЦНИИПС им. Н. П. Мельникова в 1989 г. подготовил руководство по расчету стальных конструкций на хрупкую прочность [23]. Активную исследовательскую работу по изучению сопротивляемости стали хрупкому разрушению в агрессивных средах [24], пластическим деформациям [25, 26] ведут вузовские коллективы России. Рекомендации по учету пластических деформаций при расчете фланцевых соединений изложены в статье [27]. Развитие пластических деформаций в стальных составных стержнях показано в работе [28]. Напряженное и деформированное состояние предварительно напряженных стержней рассмотрено в работах [29–32].

Цель работы – предложить методику оценки ресурса балок, предварительно напряженных вытяжкой стенки при пластической работе ее материала в зоне максимального момента внешних нагрузок.

Материалы и методы

Разработчиками эффективных балочных конструкций установлено, что 75 % несущей способности составных балок приходится на поясные листы и только 25 % - на стенку конструкции. Следовательно, на основании принципа совмещения функций, применяя в поясах балок высокопрочную сталь, можно многократно увеличить их способность воспринимать внешнюю нагрузку. В данном случае речь идет о проектировании биметаллических стальных изгибаемых элементов. Очевидно, что в предельном состоянии конструкции при условии, что материалом поясных листов является высокопрочная сталь, которая находиться в упругом состоянии, в материале стенки возникнут пластические деформации.

Для решения задачи о несущей способности биметаллической балки с частичной текучестью материала стенки рассмотрим ее поперечное сечение, показанное на рисунке 1.

Обозначим расчетное сопротивление материала пояса балки PR y ( R y - расчетное со

противление малоуглеродистой стали в стенке балки, в = R y / R_y; R^v v - расчетное сопротивление материала поясных листов из высокопрочной стали).

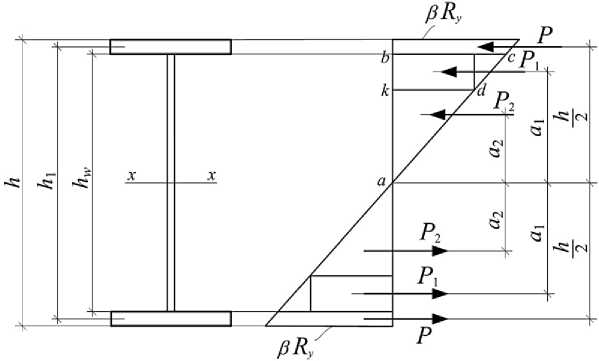
Рисунок 1 – Расчетная схема биметаллической балки

Из подобия треугольников abc и akd можем записать,

ab ak        h    ak

— = —, или =    .

bc kd      2 p R_y R y

Откуда находим, что

ak = —

2в

В крайних фибрах стенки высота зоны текучести ее материала

e = bk = — — ak = 2

h ( в — 1)

2 в ’

Расстояние от центра тяжести зоны текучести стенки до нейтральной оси балки

, e h ( в + 1) a = ak +  =--

¹       2      4 в

Расстояние от центра тяжести зоны упругой работы материала стенки до нейтральной оси балки равно

2akh a2 ==

2    33

.

На основании теории сооружений момент внутренних усилий определяется из эпюры

нормальных напряжений в поперечном сечении балки

M < | M | = Ph + P₂ x 2 a 1 + P₂ x 2 a ₂ .

Усилие P , действующее по центру тяжести поясных листов,

P = A f Y _f e ^Ry =

AR y P (1 — Y w )

.

( y f = Af / A - коэффициент распределения материала по поясным листам,

Yf = ( - - Yw) / 2 ; Y _w = A w /A - коэффициент распределения материала по площади A w ).

Усилие P ₁ действует по центру тяжести зоны текучести материала стенки

стенки

. у _ Y - A ( в — 1) R y

P = et w R =---- 2 в---

.

Усилие P ₂ действует по центру тяжести упругой зоны материала стенки

1          y A-R_v

P = - akt_wR_v = ——y 2 2 ^w y    4 в

.

Таким образом,

[M ] =

AR y в (1 - Y w ) h   Y w AR y ( в — 1)

= AR y h (6 в 3

2 в

2 AL ( в + 1) + ARY- 2 AL = 2 в         4 в   3 в

- Y w )(6 в ³ - 3 в ² + 1) 6 в ²

Высоту поперечного сечения биметаллического двутавра запишем в виде

h = Y ww² ^An w

.

( n_w - гибкость стенки балки). Следовательно,

[M ] =

RAAn w г 6 в y

— Y w ^/2(6 e ³ — 3 в ² + 1) 6 в²

.

Первая производная от момента внутренних усилий [M ] по переменному параметру, характеризующему распределение материала по стенке балки Yw, позволит определить его оптимальное значение d [M ] Ry Ayl An w dYw     2 • 6в 2

6    1/2

^Y w

-

3 Y W '²(6 в ³

-

3 в ² + 1) =0;

■ =       2 в³

W    (6 в ³ - 3 в ² + 1)

.

Коэффициент распределения материала по поясам балок

₌ 1 - Y w ₌   4 в ³ — 3 в ² + 1

.

^{Y f}     2      2(6 в ³ - 3 в ² + 1)

Уместно отметить, когда в = R v / R y = 1,0 , что характерно для традиционной симметричной монометаллической балки, y_w = 0,5, Y f = 0,25.

Подставляя зависимость (12) в выражение (9), находим, что

[M ]=        , или же, с учетом высоты поперечного сечения балки по формуле (10) [M ]= RyAAAnw. x Cm, где

C bm =

2 в⁵

1/2

3 L б в - 3 в ² + 1 _

.

Если в поясах биметаллической балки применить сталь С590 (ГОСТ 27772)

(Rvy = 59,0 кН / см2 ), а в стенке - С235 ( Ry = 23,5 кН / см2), то несущая способность балки ока- жется равной

[ M ] = R_yA ^3/2 n ^1/2 X ¹

2 ■ (

23,5

)5

1/2

59 7

6( ⁵⁹ )³

23,5

—

3(

59 ₎ 2

23,5

+ 1

= 0,379 x A ^3/2 R y n ^1/2

Это в 1,6 раза выше несущей способности традиционной монометаллической балки.

Высота зоны текучести материала стенки при расчетном сопротивлении материала поясов R^v_y = 59 , 0 кН / см ² будет равной

e = h( в-V = h x (251-1) = 0,3h .

2 в 2     2 , 51

Полученный результат свидетельствует о том, что в случае применения в поясных листах биметаллических балок стали по ГОСТ 27772 шарнир пластичности в зоне максимального изгибающего момента исключен. Зона упругой работы материала стенки никогда не будет меньше 0 , 4 h .

В биметаллических балках, предварительно напряженных вытяжкой стенки, текучесть материала стенки наблюдается только в ее нижней области.

Профессор В. А. Кравчук [26] установил, что высота зоны пластического деформиро-

вания в указанных балках	e. = h x -K + 1 = 0,235h,                           (18) 1        5K + 3    ’     ’
протяженность зоны	x = 1,476 x hh ,                                 (19)
а ее площадь	l / 2,08 F = f 011 x 2 dx = 00 x 1(—)3.               (20) 0 l             l 3 2,08

Заметим, что в предварительно напряженных балках высота зоны текучести материала стенки на 21,6 % меньше, чем в традиционных конструкциях.

Поскольку нижний поясной лист предварительно напряженной балки выполняется из высокопрочной стали, находящейся в состоянии упругого деформирования, пластические деформации стенки в районе нижнего пояса находятся в стесненных условиях. Нижний пояс выполняет роль условной затяжки, не позволяющей осуществлять распространение пластических деформаций в стенке. Пластические деформации являются источником концентраторов напряжений и возможного хрупкого разрушения металла стенки балки.

На основании работ Н. А. Махутова [14] определен коэффициент концентрации напряжений af = ^wn = 3444 = 1,497 < Опах = Run = 36 = 1,565 .              (21)

^f R_y    23             ^max R_y 23

( ^a Wwn — максимальное нормальное предварительные напряжение в нижней зоне стенки балки,

^ = R ^{3 K + 2} = 34 , 44 кН / см ²).

w    ^y( 2 K + 1 )

Работы Р. Петерсона [19] позволяют установить, что коэффициент безопасности предварительно напряженных балок

I R ,     1 , 22 X 36

34,44

= 1 , 275 .

Здесь R un - временное сопротивление разрыву стали С235, R un = 36 кН/см²; L b - коэффициент предельного состояния при изгибе. При высоте зоны пластических деформаций e = 0,235 x h , согласно [18], Р. Петерсон рекомендует принимать L b = 1,22.

Учитывая коэффициент концентрации напряжений af = 1,497 , который меньше поро говых значений amax = 1,565 (Н. А. Махутов) и коэффициент безопасности балок n = 1,275 (Р. Петерсон), можно надеяться, что ресурс предварительно напряженной балки, имеющей пластические деформации в стенки д = n^max = 1,ззз8. (23) af

В предварительно напряженных балках, жестко закрепленных в опорных узлах, кроме усилий от внешней нагрузки и предварительного напряжения, действует еще опорный момент M _op , вектор которого направлен в сторону, противоположную вектору внешней нагрузки.

Указанный момент создает нормальные напряжения, превосходящие напряжения a'wn , нижняя зона балки оказывается сжатой, растягивающие напряжения, создающие пластические деформации в нижней зоне стенки теперь уже находятся в зоне сжатия и погашаются. Имеет место «замыкание» пластической зоны. Материал всей предварительно напряженной балки находится в упругой области. Ресурс балки значительно повышается.

В процессе цикла «разгрузка-нагрузка» предварительно напряженной балки в зоне пластического деформирования материала нижней области стенки появляется разгружающее усилие P ₅ (рис. 2), которое создает изгибающий момент M ₅ , а также сжимающие напряжения в верхней и растягивающие – в нижней областях конструкции.

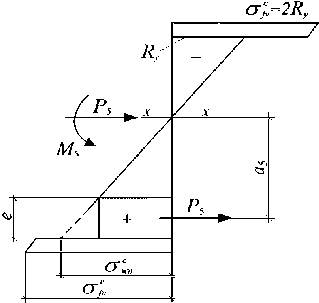
Рисунок 2 – Упругопластическая разгрузка балки

Алгебраическое сложение указанных напряжений с предварительными напряжениями балки, позволяет уменьшить напряжения пластического деформирования материала стенки на 65 % и снизить высоту зоны текучести ее материала. Закон монотонного уменьшения высоты зоны пластического деформирования f (n) = 0,24hpr x(0,65)n, (24) где n - количество циклов «разгрузка-нагрузка» балки.

Численные значения пошагового уменьшения зоны текучести стенки показаны в таблице. График указанного процесса представлен на рисунке 3.

Таблица

Пошаговое изменение коэффициента f

n	1	2	3	4	5	6	7	8	9	10
f(n)	0,126 h	0,099 h	0,0645 h	0,042 h	0,027 h	0,017 h	0,011 h	0,075 h	0,005 h	0,003 h

Незначительные циклические воздействия на предварительно напряженную балку снижают уровень пластических деформаций стенки, материал конструкции приближается к упругой работе и выносливость конструкции будет повышаться. Поскольку материал стенки предварительно напряженной балки находится в двух состояниях – пластического и упругого де-

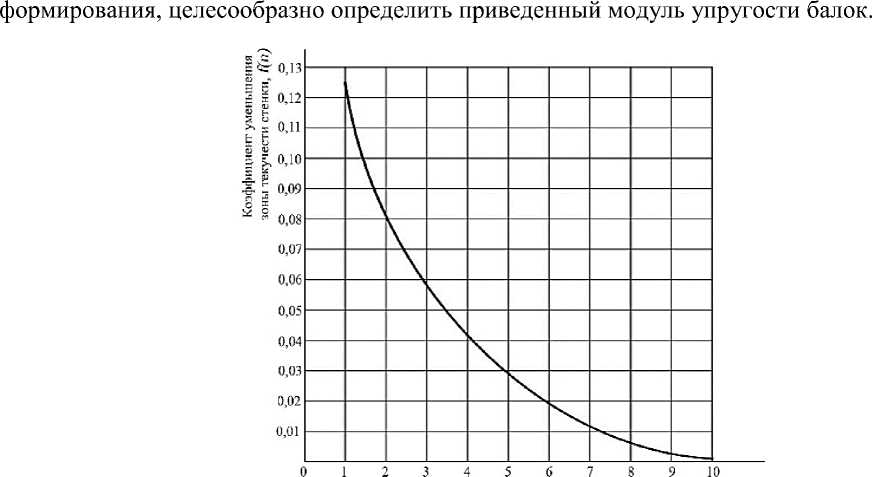
Количество циклов «разгрузка-нагрузка» балки, Л

Рисунок 3 – Изменение высоты пластической зоны в нижней области стенки при циклическом нагружении балки

Поиск приведенного модуля упругости балки Т решается на основании предположения о том, что изгибная жесткость ТI x предварительно напряженной балки, имеющей зону пластического деформирования некоторой части материала стенки, равна изгибной жесткости ЕI xо этой балки, весь материал которой находится в упругой области.

TI x = EI xo . (25)

Здесь Т — приведенный модуль упругости балки, материал которой находится в состоянии упругопластического деформирования; I x , I xo — момент инерции поперечного сечения балки при упругопластическом деформировании материала и при упругой его работе.

Момент инерции поперечного сечения предварительно напряженной балки (рис. 4), весь материал которой находится в состоянии упругого деформирования запишем в виде

I xo = A fv ^{х y} 1 + ^{0,755 х} ht w ^х У 3 + ~    12       + A fn y 5 .             ⁽²⁶⁾

Здесь Afv — площадь сечения верхнего пояса балки, Afv = 0,292х A; А — площадь поперечного сечения предварительно напряженной балки; у 1 — расстояние от нейтральной оси тавра, образованного верхним поясом балки и участком стенки (h — e) = 0,755 х h (е — высота площадки текучести материала стенки предварительно напряженной балки, e = 0,245 х h, до цен- тра тяжести верхнего поясного листа (yi = 0,2378х h); Aw = 0,496х A; y - расстояние от нейтраль- ной оси тавра до центра тяжести стенки,

0,755 х h у3---—--y1 — 0,1397 х h; 0,755 х h -

часть стенки

балки, материал которой находится в упругой области; t w - толщина стенки балки; A fn - площадь нижнего пояса балки, A fn = 0,211 х A ; у 5 - расстояние от центра тяжести тавра до нижнего пояса, у 5 = h - у i = 0,7622 х h ; у 4 - расстояние от нейтральной оси тавра до центра тяжести пластической зоны стенки, у 4 = 0,3947 х h .

_ ( 0 , 7555 h)(K + 1 )

Кроме того,

у^ —                    — 0 , 51/2 х h.

• ²       ( 2 + K)

  Таким образом,

  
  
  

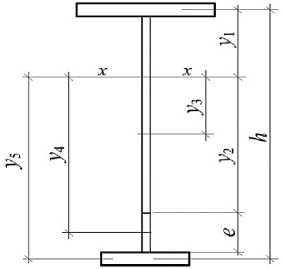
  Рисунок 4 – Расчетная схема поперечного сечения упругой зоны предварительно напряженной балки

  
  

  I xo — 0,161 х Ah ².

  Момент инерции предварительно напряженной балки

  Т — 2 ^Ah - — 0 , 1655877 х Ah ² .

  ^x 3 (K + 1 ) ²

  Приведенный модуль упругости

  I_xo       0 , 161 х Ah ²

  T — xo E — ^^^—^^^—v — 0 , 972 х E.

  I_x     0 , 1655877 х Ah ²

  x

  
  
  
  
  
  
  
  

Из работ В. А. Кравчука известно, что напряжение, создающее пластические деформации в нижней зоне стенки балки, определяется выражением

3 K + 2       3 - 1 , 175 + 2            тт / 2

• а, — R., х       — 23 х           — 37 , 932 кН/см .

wn ^у 2 K + 1        2 - 1 , 175 + 1

Относительная деформация ε пл , материала стенки балки, находящейся в состоянии пластического деформирования, с учетом приведенного модуля упругости T будет равна

_£ — —^w— — 0 , 0018583 .

пл 0 , 972 х E

Полученное значение относительной деформации меньше прогнозируемой

• 3    R ^_ст= ----— — 0 , 00338,

ост 0,972 х E установленной на основе метода расчета металлических конструкций с учетом ограниченных пластических деформаций.

Запас фактических относительных деформаций

Z — ^ _ост / е пл — 0,00338/0,0018583 — 1,819.

Это означает, что по критерию пластических деформаций, ресурс их развития в материале стенки предварительно напряженной балки равен 1,819.

Полученное значение приведенного модуля упругости материала справедливо для предварительно напряженной балки, нагруженной статическими нагрузками. Когда же конструкция будет находиться под действием циклически приложенных внешних нагрузок, то на основании наших выводов о выносливости балки зона пластического деформирования стенки балки будет монотонно снижаться и приведенный модуль T будет приближаться к модулю упругости E _.

Поскольку нижняя область стенки балки находится в состоянии пластического деформирования, существует вероятность хрупкого разрушении материала стенки. Согласно четвертой энергетической теории Губера, Мизеса и Генки, пластическая сталь начинает разрушаться тогда, когда приведенные напряжения ai достигают значений, определяемых выраже- нием ai = ^ 42 [a1 + a2

- a 1 a 2 )

=^72 ^a W i-+(⁰²5* ^a W 3^^         =

= 30,69 кН/см ² <  R u = 35 , 0 кН/см ²

( a 1 , a ₂ - главные напряжения, R u - временное сопротивление разрыву стали С235).

Общеизвестно, что в области действия максимального изгибающего момента вектор главных напряжений совпадает с вектором нормальных напряжений и указанные напряжения равны между собой. Следовательно, продольное главное напряжение a1 = Own = 34,44кН / см2. Поперечное главное напряжение а2, с учетом коэффициента Пуассона, будет равно a2 = 0, 25 х assn = 34,44 х 0,25 = 8,6175кН / см 2.

Поскольку фактические приведенные напряжения ai меньше временного сопротивления стали Ru, хрупкие трещины в нижней зоне стенки предварительно напряженной балки бу- дут отсутствовать.

Фактические напряжения в поясных листах и стенке предварительно напряженных балок меньше предельных расчетных сопротивлений стали на растяжение и сдвиг и, следовательно, хрупкое и вязкое разрушения при упругой работе материала исключены.

Локальный предел текучести al = KiaT = 0,283 х23,5 = 6,66см2 << Ryn = 23,5кН/см2.           (31)

Здесь Ki - коэффициент жесткости напряженного состояния.

Ki =

(1 - а)2 + (а - в)2 + (в -1)2

(1 - ^)2+(

8 , 6

= = 0 , 283 .

34 , 44 ,2

IT )         ⁽³²⁾

а = a j / а ₂ ; в = а ₃ / a 1 .

Здесь a r - предел текучести стали С235 при одноосном нагружении;

aT = Ryn = 23,5 кН / см 2.

Значение локального предела текучести материала стенки свидетельствует об ограниченных пластических деформациях и малой вероятности хрупких разрушений в этой области.

Заключение

• 1.    Применение в поясных листах биметаллических балок высокопрочной стали по ГОСТ 27772 не сопровождается шарниром пластичности в поперечном сечении конструкции.

• 2.    Пластические деформации нижней области стенки предварительно напряженных балок не вызывают хрупких трещин в ее материале.