Review of image reconstruction methods in X-ray computed tomography with cone-beam geometry
Автор: Simonov E.N., Avramov M.V.
Рубрика: Информатика и вычислительная техника
Статья в выпуске: 2 т.18, 2018 года.
Бесплатный доступ
The article reflects the main task of the X-ray computed tomography and its mathematical description. Direct and inverse Radon transform are given. The methods of image reconstruction in X-ray computed tomography are presented. Their brief classification are given. The author have reviewed classical problem of two-dimensional computed tomography and basics approaches to its solution. Emphasis is placed on back projection algorithm with filtering convolution. The derivation of the algorithm for parallel and fan-beam reconstruction are given. The analysis of the problem of three-dimensional reconstruction are presented. The author describes the additional conditions imposed on the projection data, the computational efficiency of the algorithms and the quality of the images. The basic trajectory of the X-ray source, providing the condition Tuy, are considered. The article gives an overview of existing methods of three-dimensional reconstruction with cone-beam geometry, their advantages, disadvantages, clinical applications. Their brief classification are given. Approximate algorithms of three-dimensional reconstruction are presented. The Feldkamp algorithm, the extended parallel backprojection, and the advanced single-slice rebinning are described. The author raises the question of developing approaches and methods for obtaining images with three-dimensional reconstruction for cone-beam spiral CT.
Computed tomography, three-dimensional image reconstruction
Короткий адрес: https://sciup.org/147155262
IDR: 147155262 | УДК: 519.6 | DOI: 10.14529/ctcr180203
Текст научной статьи Review of image reconstruction methods in X-ray computed tomography with cone-beam geometry
The main task of X-ray computed tomography (CT) is to reconstruct the internal structure of the objects of study by probing penetrating radiation. From a mathematical point of view, this problem can be considered as a problem of restoring some function in two-dimensional or three-dimensional space by known values of integrals along certain lines or planes. In CT, the desired function is a linear attenuation coefficient, and the projection data are known values of integrals.
The relationship between the projection data and the desired function of the linear attenuation coefficient is described by Radon transformation, which in the two-dimensional case is a linear integral of the function along the line. The representation of a function through its Radon transformation is called inversion formulas [1].
If the line L: ( £ , x ) = l is given in the normal form, the integral of the function f ( x ) along the line L is
P (o, l ) = Jf (l cos 0-x '2 sin 0, l sin 0 + x '2 cos 0) dx '2,(1)
-X where x'2 is the y-axis after the rotation by the angle θ.
The case formula will look like f (x )=-л Tj ^':0^ d 0 dl.(2)
( ) 4n2 J J l -1'al'
-x 0
where l ' is a curve passing through a specific point ( x 1 , x 2 ) [1].
Thus, the main mathematical problem of X-ray computed tomography can be reduced to the integral equation of the form
T Ц J ц ( x , y ) dl = P ( l , 0 ) . (3)
L ( l , 0 )
Equation (3), where T is the transformation operator, can be investigated by methods of integrated geometry of Radon. However, Radon methods allow us to obtain an exact solution of the basic KT equation provided that the initial data P ( l , θ) are given precisely. But in practice, projective data
Информатика и вычислительная техника
P ( l , θ) contain different kinds of errors and are not exact. I mean ... it is not possible to accurately restore an image from P ( l , θ) projections. In practice the regularization methods of equation (3) [2, 3] are applied.
All the variety of methods used for image restoration can be divided into two main groups: analytical and iterative methods [1, 2].
The implementation of any reconstruction algorithm depends on the X-ray generation scheme implemented in the tomograph. There are 3 basic schemes: parallel, fan, cone.
-
1. Reconstruction algorithm for parallel geometry of beams
The type of function µ( x , y ), denoting the distribution of the desired physical quantity, a priori unknown. However, it is known that it is zero outside the reconstruction area Ω, which is a circle of radius T with a center at the origin (Fig. 1).
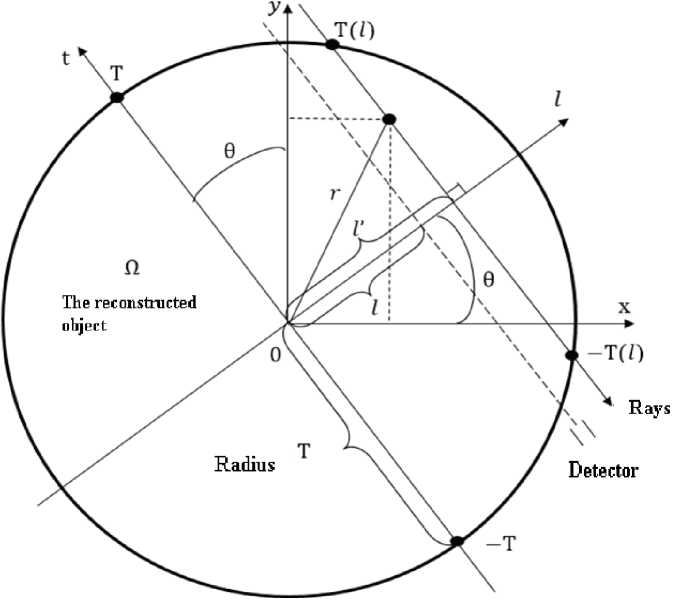
Fig. 1. Parallel scan geometry
The position of the X-ray beam is determined by its distance l from the origin and angle θ. Projection defined by the formula (1) can be written in the form
+ T
P ( l, 0 ) = j f ( l cos 0- 1 sin 0 , l sin 0 + 1 cos 0 ) dt . (4)
-
- T
The next step in constructing the reconstruction algorithm is to find the inversion formula for (4). Moreover, as shown above, the expression (2) cannot be used directly.
One of the approaches of the derivation of the reconstruction approach is based on the use of the projection theorem. The first States that the operation on the projection at angle θ is equivalent to a certain operation on the initial object µ( x , y ) . This theorem is called the generalized projection theorem. If the operation on µ( x , y ) is reversible, such as the Fourier transform, then this implies a way of finding µ( x , y ) given by P ( l , θ). The second theorem, on the Central section, is formulated as follows. Let R ( v , θ) is a one-dimensional Fourier transform of the function P ( l , θ) according to the first argument T
R ( v, 0 ) = j p ( l, 0 ) e - i 2 n vldl, (5)
-T where v = 1/2 Al is the spatial frequency; Al - the distance between the counts of the rays. Then it would be true equality
R ( v , 6 ) = ц ( v cos 6, v sin 9 ) , (6)
where ц is a two-dimensional Fourier transform of the function ц(x, y). In other words, the one- dimensional Fourier transform of projection data for variable l is equivalent to the two-dimensional Fourier transform of an object function expressed through polar coordinates.
It is obvious that the inverse two-dimensional Fourier transform from ц gives a reconstruction for- mula the function µ(x, y) on the set P(l, θ). However, in the practical implementation of this method of action there are significant difficulties associated with sampling errors and inaccuracy of projection data. The result is a very noisy image of the subject object's. To avoid this, it is necessary to take special measures [1, 2].
One of the ways solution to the problem is the use in (8) the Fourier transform of the function ц, and it will work on the window function W(v):
~Z,x-,xX''/,x-,xX„r/X
ц( v cos 6, v sin 6) = ц( v cos 6, v sin 6) W (v).(7)
Then, substituting (7) in (6), and taking the inverse Fourier transform, you can get
_ n T ц = JJ P(l, 6) g (l'-l) dld6,(8)
0 - T where
12AI g (l )= J vW (v) exp (i2nvl) dv,(9)
-
-12A I
-
2. The Algorithm of reconstruction in fan geometry of the rays
l' = x cosθ + y sinθ – ray passing through a specific point P .
An internal integral in expression (8) is called a collapsed projection and is a convolution by l of projection P ( l , θ) at the angle θ and function g ( l ) given by expression (9). Function g ( l ) is called a collapsing function, and its appearance depends on the window function W(v) (Fourier function g ( v ) = | v| W ( v ) ). The outer integral represents the inverse operation of projection. Formula (8), (9) form the basis of the method the reconstruction method of convolution and back-projection.
To date, widespread scheme of scanning with a fan beam geometry, which is more preferable from the point of view of performance. Each beam is considered as a set of divergent rays, which defines the position of the radiation source – and γ – the angle between the beam and the line connecting the source and the center of the circle (Fig. 2).
U is the position of the radiation source on a circle with radius D and center 0; β is the angle of inclination of the straight line 0U to the y-axis; θ is the angle between the perpendicular 0 R omitted from the origin of beam, and the x-axis; 0 R equal to the length l ; S - distance between points U and P ; y is the angle between 0 U and UP ; r – length 0 P ; q (γ, β) is a linear integral along the beam for fan geometry.
From formulas (7) to (9) for parallel geometry of the rays should
-
. to T 2n
-
ц ( r cos ф , r sin ф ) = — J J J P ( l , 6 ) exp ( i 2 n v [ r cos ( 6-ф ) - 1 ] ) W ( v )| v|d 6 dldv .
-
2 to T 0
Going from the variables ( l , θ) variables (γ, β), the operation of the reconstruction can be represented in two stages:
-
Y m
q ( y ', P ) = J q ( y , P ) cos y- g ( S sin ( y'-y ) ) d y ; (10)
-
-Y m
-
p. 2n
D
-
ц ( x , y ) =y J q ( y , P ) d P , (11)
Информатика и вычислительная техника
where да g ( S sin (у '-y))= j |v|^ (v) exp (i 2n vS sin (y -y)) dv.
-да
If you accept y = Y ' - y , v' = vS sin y/y , you can write
~ 2 да
g ( S sin Y ) = Y , f v 'I exp ( i 2 n v' y ) dv'.
-
x 1 S 2 sin2 Y -да x ’
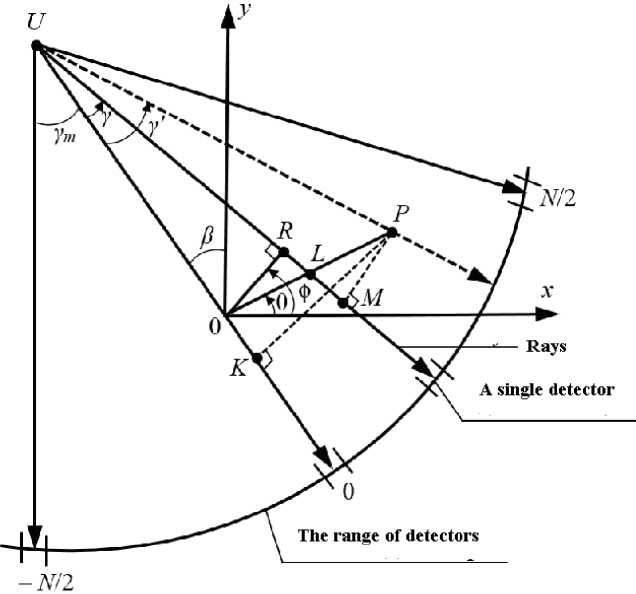
Fig. 2. Fan-shaped scanning geometry
The integral in (13) represents the kernel with the argument y obtained for parallel beams , and is the inverse Fourier transform of the spatial frequency module v ' . The kernel for the fan-shaped geometry of the beams can be determined 2
g ( Y ) , g ( Y ) . x ' S sin y
As a result, formula (11) will take the form of a fan scan geometry
-
1 2 n 1 Y m ~
ц ( x , y ) j 2 d P j q ( Y , P ) g ( y ' -y ) d Y ,
-
2 0 S —Y m
where q ( y , P ) = q ( y , P ) D cos Y is the modified projection;
-
Y 2
-
3. The reconstruction algorithm when the conical geometry of the beams
g f ( y ' — y ) = g ( y ' — y ) --2“ is the modified kernel.
sin2 y
The above algorithms for parallel and fan geometry of rays formed the basis of the classical approach to solving the problem of computed tomography, in which measurements are made in the same plane with the help of linear detectors, and according to these data, the layer of the object is reconstructed.
In practice, there are cases when the information in one slice of the studied object is not enough and it is necessary to understand the internal structure of the whole extended object. To obtain the necessary three-dimensional image, it is possible to carry out a series of measurements by the classical method and then combine the information obtained about the individual layers. This approach to solving a volume problem significantly increases the time of tomographic examination, which is not always acceptable in practice.
Another way to obtain a three-dimensional image is a three-dimensional reconstruction. In contrast to the classical two-dimensional CT method of measurement method of three-dimensional CT is produced in a cone of X-rays using a two-dimensional detector, which allows to obtain the projection of multiple layers in a single measurement. This approach provides some advantages over the classical research method: increases the photon flux, reduces the time of projections and makes it possible to increase their geometric.
In order to accurately restore the image along cone projections, it is necessary that each plane passing through the studied object at least once crosses the trajectory of the radiation source (Kirillov – Smith – Thuy condition [4, 5]). Examples of scanning schemes with the trajectory of the source that satisfy this condition: spiral, two circles, a circle and a straight line, two circles lying in mutually perpendicular planes [4].
Both algebraic and analytical methods were developed to solve the three-dimensional CT problem. These methods can be divided into two classes. The first one includes algorithms that divide a threedimensional problem into a series of two-dimensional ones. From a set of cone projections by interpolation is obtained by a set of fan projections, on which a two-dimensional reconstruction of parallel layers of the object is performed. This approach is called the method of repackaging.
The second class includes algorithms that perform a complete three-dimensional reconstruction. Two-dimensional cone projections are filtered in some way, and then a reverse projection operation is performed. Such algorithms are often referred to as the FBP algorithms (filtered backprojection) or algorithms of the inverse projection with filtering [4, 5].
In [6] Feldkamp with co-authors proposed one of the first algorithms of three-dimensional reconstruction with cone geometry of rays. The article presents an algorithm for a source moving along a circle. This trajectory does not satisfy the data completeness condition because the planes parallel to the planes in which the source moves intersect the study object, but do not intersect the trajectory of the source. Therefore, accurate image recovery is not possible and the algorithm is approximate.
The Feldkamp algorithm belongs to the class of FBP algorithms. It performs a line-by-line convolution filtration, and the full geometry of the cone scheme is taken into account only at the stage of the inverse projection calculation.
Let a stationary object be specified for the study. The source-detector system revolves around the object, describing the circle. The plane containing the source is called media her plane. The intersection of the middle plane and the axis of rotation is taken as the origin. The distance from the source to the detector is D , from the source to the axis of rotation – d , from the axis of rotation to the detector – d ' (Fig. 3).
With d → ∞, the algorithm passes into a layer-by-layer inversion formula for the parallel case. In addition, the algorithm gives the exact value of the density function in the Central section ( z = 0) at any distance from the source.
For Fig. 4 f -rotation angle, Y -coordi-nate along the detector that determines the recovery point.
The plane of the detector
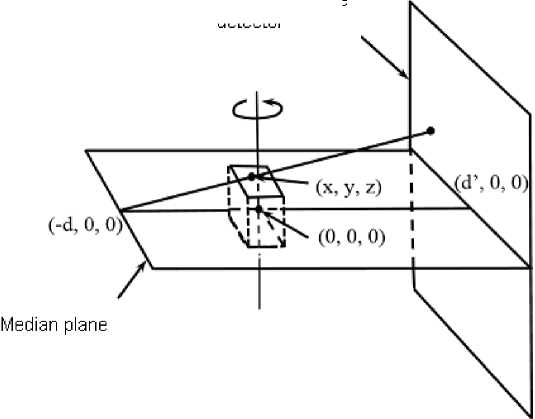
Fig. 3. The geometry of the scanning cone of rays
Информатика и вычислительная техника
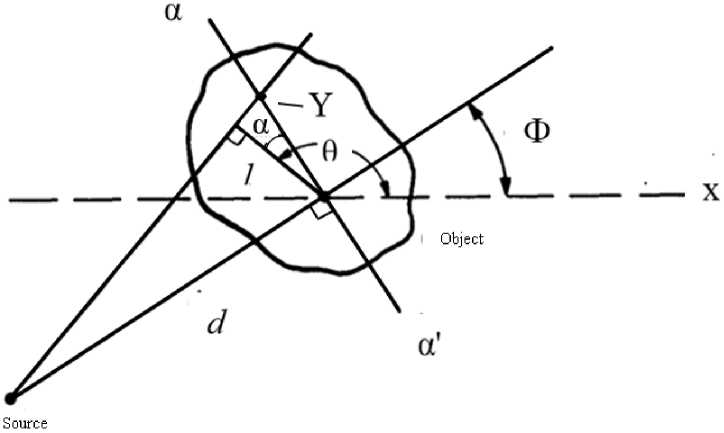
Fig. 4. The geometry at the mid-plane
Communication ( l , θ) with ( Y , Ф)
l = Yd/ ( d 2 + Y 2 ) 2, Y = ld[ ( d 2 - 1 2 ) 2 , 0=Ф+П+а . (16)
The projection in cylindrical coordinates can be written as p (l, 0) = j rdr (j> f (r, ф)б[ r cos (0-ф)-l ] d ф.
Using the formula of inversion (3) in polar coordinates, when the point x = (r, ϕ) and l = rcos(θ – ϕ), and presenting the projection p (l, θ) through the Fourier transform (7), you can write the desired density function as да +да f (r, ф) = 2 Re ф d0j vdv j p (l, 0) ejv[cos(0 ф) l ]dl.
4 n 0 -да
Performing the transition from the coordinates (l, θ) to (Y, Ф) by expressions (16) and from v to v' by v' = v [ d + r cos (ф-Ф)]/ (d 2 + Y2)2, we can write down the final formula for the fan bundle in the median plane f (r, ф) = -2 # --------------PP.[ Y (r, ф)] d ф, (17)
4 n [ d + r cos ( ф-Ф ) ]
where
Y (r, ф ) = dr sin ( ф-Ф )/ [ d + r cos ( ф-Ф ) ] ,
-
- , , да
P - ф ( Y ) = j----------- Г Р ф ( Y ') g ( Y - Y ') dY' (18)
-
-да ( d 2 + Y '2 ) 2
vy 0
g ( Y ) = Re j v exp ( jvY ) dv . (19)
Expression (17) is an inverse projection operation, (19) is a folding function, (18) is a rolled-up projection. Further, to determine the formula for three-dimensional reconstruction, it is necessary to determine the additional contribution of δf to the reconstructed density by the projection data for a small increment of the rotation angle δΦ. From the projection data along the intersection of the plane of the detector, with the middle plane, we can calculate the contribution at points lying on the median plane. Projections that cross the plane of the detector along a line parallel to the median plane, but not lying in it, themselves determine the plane. This plane is considered as an average plane-in a tilted coordinate system. It is necessary to correct the difference between the actual rotation of δΦ along the vertical axis and an equivalent rotation of δФ' along the normal to the plane.
Further, the distance from the source to the detector in the inclined plane is substituted into the Radon's transformatuion. The density at the point r is taken equal to the sum of the additional contributions of all planes (one for each rotation angle) passing through r . Feldkamp's algorithm became one of the first algorithms of three-dimensional reconstruction, suitable for practical implementation. The algorithm gives an approximate solution for a circular trajectory, provides high quality of restoration, but does not take into account the cone angle (with the error of reconstruction grows with the angle), although it surpasses the classical approach and some iterative methods, it takes a lot of time for the computer account. In this connection, several modifications of the Feldkamp algorithm were proposed. The main Managing is given to the creation of high-speed algorithms and to the investigation of possible general the complexity of the method of collecting projection data [2, 5, 6].
So in [7] an algorithm was proposed, which was called the generalized parallel inverse projection (EPBP – extended parallel backprojection). From the classical Feldkamp algorithm, this the method is characterized by the use of repackaging and the transition to parallel data, which allows correctly take into account the redundancy of data, use an arbitrary pitch for spiral scanning, perform a reconstruction of the images of the heart.
An alternative to algorithms based on the Feldkamp method can be the single-layer repacking algorithm (ASSR – advanced single-slice rebinning). Term “One-layer repacking” implies the separation of the trajectory of the source into almost flat segments, each of which can be approximated by a flat curve. The oblique plane, holding such a curve, is called the reconstruction plane. Cone data transfom to these slanted planes that results in a set of fan projections. Behind the reconstructed flat tomograms are transformed into the required three-dimensional shape [2, 8].
Algorithms such as ASSR and EPBP give an approximate solution to the problem of three which is expressed in artifacts on the image. Development of an exact analytical algorithm ensuring optimal image quality is a complex task that has been the subject of intensive research in the world for several decades and has worthwhile time. The exact methods currently being developed are under investigation.
Conclusions
Algorithms of classical two-dimensional reconstruction of tomographic image for parallel and fan geometry of beams are considered. The analysis of the main approaches to the solution of the threedimensional problem of KT is carried out, common approximate methods for reconstruction of threedimensional images on a two-dimensional projection obtained when the conical geometry of the beams to planar and non-planar scan trajectories are considered.
The three-dimensional reconstruction of an image from cone beam projections is one of the most recent generalizations of CT. To obtain the exact solution it is necessary to use a flat trajectory that satisfies the completeness condition: every plane through the object under examination at least one time crosses the trajectory of the motion of the radiation source. Of all the promising trajectories providing accurate three-dimensional reconstruction, the most suitable for practical applications is a spiral covering the object both in radius and height. Spiral CT scan is a mode of volumetric tomography with non-planar geometry of radiation, which is performed by continuous longitudinal movement of the object of study.
The development of approaches and methods for obtaining tomographic images for threedimensional reconstruction in the cone of rays for spiral CT is an urgent task of CT, which has become the subject of intensive research of the last few decades for the developers of reconstruction algorithms.
Список литературы Review of image reconstruction methods in X-ray computed tomography with cone-beam geometry
- Симонов, Е.Н. Физика визуализации изображений в рентгеновской компьютерной томографии/Е.Н. Симонов. -Челябинск: Издат. центр ЮУрГУ, 2013. -479 с.
- Календер, В. Компьютерная томография основы, техника, качество изображений и области клинического использования/В. Календер; пер. с англ. А.В. Кирюшина, А.Е. Соловченко; под ред. В.Е. Синицына. -М.: Техносфера, 2006. -344 с.
- Тихонов, А.Н. Математические задачи компьютерной томографии/А.Н. Тихонов, В.Я. Арсенин, А.А. Тимонов. -М.: Наука, 1987. -160 с.
- Пикалов, В.В. Сравнение алгоритмов спиральной томографии/В.В. Пикалов, А.В. Лихачев//Вычислительные методы и программирование. -2004. -Т. 5. -С. 170-183.
- Лихачев, А.В. Сравнение алгоритма Фельдкампа с алгоритмом синтеза Фурье для трехмерной томографии/А.В. Лихачев//Автометрия. -2006. -Т. 42, № 1 -С. 88-102.
- Feldkamp, L.A. Practical cone-beam algorithm/L.A. Feldkamp, L.C. Davis, J.W. Kress//J. Opt. Soc. Am. A. -1984. -Vol. 1, iss. 6. -P. 612-619 DOI: 10.1364/JOSAA.1.000612
- Kachelrie, M. Extended parallel backprojection for standard three-dimensional and phase-correlated four-dimensional axial and spiral cone-beam CT with arbitrary pitch, arbitrary cone-angle, and 100% dose usage/M. Kachelrie, M. Knaup, W.A. Kalender//Medical Physics. -2004. -Vol. 31, no. 6. -P. 1623-1641 DOI: 10.1118/1.1755569
- Kachelrie, M. Advanced single-slice rebinning in cone-beam spiral CT/M. Kachelrie, S. Schaller, W.A. Kalender//Medical Physics. -2001. -Vol. 27, no. 4. -P. 1033-1041.


