Режимы всплытия тепловых плюмов в вертикальном слое

Конвективные явления, сопровождающиеся образованием характерного грибообразного теплового поля, называемого в зарубежной литературе тепловым плюмом, широко распространены в природе [1]. Течение, вызванное сосредоточенным источником тепла и на начальной стадии порождающее тепловой плюм, как правило, представляет собой струйное движение жидкости в виде конвективного факела [2, 3]. Внутренняя область плюма всегда имеет отличную от остальной жидкости температуру, что позволяет качественно устанавливать его границы и классифицировать их по форме. В зависимости от вязкости и теплопроводности среды окружающая жидкость в определенной степени также оказывается вовлеченной в конвективное движение, что, собственно, и создает тепловой плюм. Следует заметить, что помимо проявлений в природе подобные конвективные структуры имеют место в различных технологических процессах.

В естественных условиях с тепловыми плюмами часто приходится сталкиваться в геологии. Конвективные грибообразные структуры, возникающие в магматических расплавах, характеризуются гигантскими числами Прандтля. В экспериментальной работе [4] лабораторно моделируются специфические условия для формирования плюмов в жидкостях при больших числах Прандтля. Эксперименты проведены с вязкими маслами, числа Прандтля которых достигают 104. Однако величины даже такого порядка далеко отстоят от чисел Прандтля, характерных для магмы. Тем не менее, была предпринята попытка экстраполировать полученные данные на геологические приложения. В ходе экспериментов тщательно изучалась зависимость скорости всплытия плюма от теплопотерь на электрическом нагревателе, в результате чего для количественного описания интересующего эффекта предложена модификация известной формулы Бэтчелора [1]. Представлена оценочная формула, позволяющая проанализировать влияние боковых границ на процесс роста конвективного факела.

В близких по содержанию работах [5, 6] основное внимание фокусируется на экспериментальном исследовании различных характеристик шляпки плюма, а именно скорости ее всплытия, поперечных размеров, формы и распределения температуры внутри. Для визуализации течений использовался теневой метод. При оценке степени искаженности фотоизображений в жидкость добавлялись микрокапсулы размером 50–100 мкм с жидкокристаллическим наполнителем, реагирующим изменением цвета на малейшие колебания

температуры. Показано, что с течением времени характерный размер шляпки при подъеме увеличивается практически по линейному закону. Однако наиболее интересными оказались результаты экспериментов по изучению всплытия нескольких взаимодействующих плюмов. Приведены фотографии, свидетельствующие, как близко отстоящие друг от друга плюмы взаимно притягиваются ножками и по мере всплытия образуют из шляпок единый тепловой фронт.

В теоретической работе [7] численно исследуется динамика двумерных тепловых плюмов, создаваемых линейным горизонтальным нагревателем. Поля температуры и скорости в поперечном сечении ножки описываются гауссовым распределением и при определенных условиях демонстрируют ярко выраженный погранслойный характер. На основе результатов численного 2D моделирования проводится градация возможных режимов всплытия тепловых плюмов. Согласно введенной в этой работе классификации режимы всплытия плюмов условно делятся на четыре типа: вязко-теплопроводный, вязко-нетеплопроводный, невязкотеплопроводный и невязко-нетеплопроводный. Критерием разделения на типы служит соотношение скоростей роста температурного и гидродинамического пограничных слоев ножки, которое в конечном счете определяет форму шляпки и скорость всплытия конвективного факела. Расчеты проведены в широком диапазоне чисел Прандтля и Рэлея и обобщены на карте режимов. Динамика рассмотренных в данной статье режимов подтверждает справедливость этой простой классификации.

С другой стороны, существует цикл публикаций [8–10], связанных с разработкой конвективного датчика низкочастотных ускорений. Очевидно, что эффекты, возникающие на начальной стадии формирования тепловых плюмов, могут повлиять на работу этого датчика. Особенно сильно от типа формирующегося плюма зависит время выхода на установившийся режим. В [8, 9] численно, методом конечных разностей, изучалось влияние коротких инерционных внешних сигналов (механических вибрационных воздействий) на конвективные течения в ячейке Хеле-Шоу при подогреве снизу пульсирующим сосредоточенным источником тепла. При подобном нагреве в полости устанавливалось нестационарное течение в виде пульсирующего конвективного факела. Расчет температурных полей и формы течений в приближении плоских траекторий проведен для коротких периодических сигналов, ориентированных вертикально и горизонтально в плоскости широких граней. Показано, что при наличии горизонтальных вибраций нарушается симметрия конвективного факела относительно вертикальной оси, а в случае вертикального периодического воздействия меняется скорость всплытия теплового пятна; при этом симметрия течения относительно вертикальной оси сохраняется.

Влияние произвольно ориентированных в плоскости широких граней инерционных сигналов рассмотрено в работе [10]. Внутри полости выделялось три узла, расположенных таким образом, чтобы однозначно определялось смещение конвективного факела, вызванное инерционным сигналом. С трех точек снимались температурные амплитудно-частотные характеристики в зависимости от направления и интенсивности вибрационного воздействия. Это позволило разработать методику расчета частоты, амплитуды и направления инерционного сигнала с использованием минимального количества термодатчиков. Показано, что предложенная методика может быть полезной при проектировании прибора, способного регистрировать инерционные воздействия в виде переменных по времени коротких сигналов. Специально переходные режимы в работах [8–10] не изучались. Расчеты продемонстрировали необходимость более детального исследования процесса формирования струйного конвективного течения в ячейке Хеле-Шоу, которое характеризуется возникновением и всплытием тепловых плюмов.

• 2.    Основные характеристики платформы OpenFOAM

• 3.    Геометрия задачи. Основные уравнения

Расчеты выполнены в 3D-постановке с помощью программного пакета OpenFOAM. Платформа OpenFOAM (Field Operation and Manipulation) — перспективное, динамично развивающееся открытое программное обеспечение для моделирования задач механики сплошных сред . Основным языком пакета является C++. Программное обеспечение устанавливается на Unix-подобные системы. В пакете имеются готовые решатели для различных гидродинамических систем. Всего OpenFOAM содержит более 80 приложений для моделирования различных процессов в механике, а также более 170 утилит для подготовки и обработки данных, генерации расчетных сеток и визуализации результатов расчетов. Дифференциальные уравнения в частных производных записываются в терминах математических операторов и решаются методом конечных объемов на произвольной расчетной сетке с многогранными ячейками. Работать в OpenFOAM можно как со структурированными, так и неструктурированными сетками. Значительное расширение возможностей пакета OpenFOAM обеспечивается за счет внесения изменений в стандартные решатели, например, добавления в уравнения дополнительных слагаемых . Для связывания переменных скорости и давления в OpenFOAM реализованы неявные численные методы SIMPLE, PISO и PIMPLE [11]. Платформа работает с программным интерфейсом MPI, что позволяет разбивать расчетную область на части и производить вычисления параллельно.

Решение задачи состоит из трех этапов: создания расчетной сетки, самой вычислительной процедуры и визуализации полученных данных. В OpenFOAM входят утилиты для создания сетки, но кроме них также можно использовать другие программы. Визуализация результатов осуществляется с помощью приложения ParaView , которое устанавливается вместе с платформой OpenFOAM.

Для визуализации существуют и другие программы. Для этого необходимо конвертировать соответствующие файлы в нужный формат с помощью утилит OpenFOAM.

Пакет OpenFOAM уже использовался авторами ранее для проведения тестовых расчетов трехмерных стационарных и нестационарных течений в подогреваемой снизу ячейке Хеле-Шоу [12]. В ходе реализации метода конечных объемов задача сводилась к решению систем линейных алгебраических уравнений. При аппроксимации производных по времени использовалась неявная схема Эйлера первого порядка точности. Для аппроксимации пространственных производных использовалась формула Гаусса– Остроградского. При нахождении значений искомых полей в точках, отличных от центров контрольных объемов, применялась линейная интерполяция. Решение системы линейных уравнений и определение давления проводились методом сопряженных градиентов с предобуславливанием. Расчет скорости и температуры выполнялся методом бисопряженных градиентов с предобуславливанием.

Численное моделирование динамики тепловых плюмов в вертикальном слое при локальном подогреве снизу реализуется по этой же методике.

Рассмотрим полость в форме прямоугольного параллелепипеда с твердыми гранями (Рис. 1). Введем обозначения: H , L , d — длина, высота, толщина ячейки соответственно; l — размер нагревателя. Такую

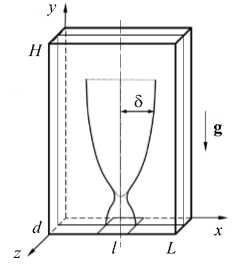
Рис. 1. Геометрия конвективной полости; система координат

полость принято называть ячейкой Хеле-Шоу, если выполняются условия H , L » d и движение двумерно. Полость нагревается неоднородно, локально снизу, как показано на рисунке 1, и находится в статическом поле силы тяжести. В ходе расчетов все вертикальные грани предполагаем идеально теплоизолированными.

Сосредоточенный нагрев и теплоизолированность вертикальных граней приводят к тому, что даже в достаточно узких полостях третьей компонентой скорости при моделировании тепловых плюмов пренебрегать нельзя. По этой причине полное 3D численное моделирование представляется наиболее приемлемым для описания струйных конвективных движений в полости прямоугольной формы. Течение жидкости в данной постановке описывается системой стандартных уравнений тепловой конвекции в приближении Буссинеска [13]:

V +(V∇)V=- ∇p+ν∆V+gβTγ,(1)

∂tρ

∂T +(V∇)T=χ∆T, divV=0.(2)

∂ t

Здесь V , p и T — размерные поля скорости, давления и температуры; ν , β и χ — коэффициенты кинематической вязкости, теплового расширения и температуропроводности соответственно; g — ускорение силы тяжести; γ — единичный вектор, направленный вертикально вверх; ρ — средняя плотность жидкости. Система (1), (2) получается путем редукции заложенных в пакете OpenFOAM более общих уравнений; в частности, пакетом предусматривается возможность расчета движения сжимаемых сред и турбулентных течений.

Неоднородность нагрева полости обеспечивается путем задания разности температур нижнего центрального нагревателя ( ϑ ) и верхней охлаждающей стенки ( ϑ ₀ ): ∆ϑ = ϑ - ϑ ₀ . Для компонент вектора скорости на твердых гранях справедливо условие прилипания: V | _Γ = 0.

Система уравнений (1), (2) решалась посредством прямого численного моделирования в размерном виде с использованием программного пакета OpenFOAM на суперкомпьютере «ПГУ–Тесла» Научнообразовательного центра «Параллельные и распределенные вычисления» Пермского государственного национального исследовательского университета. Расчеты проводились для полости с геометрическими размерами L = 24 мм, H = 32 мм, d = 4мм, при этом ширина линейного нагревателя полагалась равной l = 2мм. Выбранное соотношение сторон позволило частично сравнить результаты численного моделирования с экспериментальными данными для одиночных плюмов в гептане [14]. Выявлено хорошее качественное согласие по таким характеристикам плюмов, как форма и скорость всплытия. Количество ячеек в рабочей сетке составляло 89 × 110 × 25 . Предварительно, с целью контроля сходимости результатов, были выполнены расчеты на более мелких и грубых сетках. В таблице 1 приведены значения максимумов всех трех компонент скорости в фиксированный момент времени, когда размеры плюма достигают приблизительно 23 высоты полости.

Таблица 1. Максимальные значения компонент и модуля скорости для разных вариантов разбиения расчетной области

Номер вычислительного эксперимента	Сетка ( L х H х d )	vx , м/с	vy , м/с	vz , м/с	V , м/с
1	71 х 88 х 20	0,003302	0,013623	0,000964	0,013623
2	89 х 110 х 25	0,003566	0,014382	0,001022	0,014382
3	111 x 137 х 31	0,003616	0,014752	0,001087	0,014752

Представленные в качестве примера табличные данные для гептана при ЛЭ = 30 ° C демонстрируют хорошую сходимость по всем трем значениям компонент скорости. В частности, отличие максимума модуля скорости в 1-м и 2-м вычислительных экспериментах составляет 5,3%, а отличие этой же характеристики для 3-го и 2-го разбиений расчетной области уже равняется 2,5%.

Обработка массивов данных, необходимых для построения графиков и карты режимов всплытия, а также определение ширины пограничных слоев проводились с помощью программы аналитических вычислений Maple-11. Физические параметры сред во всех сериях вычислений выбирались так, чтобы соответствовать реальным жидкостям и газам [15, 16], таким как гептан, керосин, воздух и ртуть с соответствующими числами Прандтля: Pr = 6,8; 26; 0,73; 0,026 (см. Табл. 2).

Таблица 2. Параметры исследуемых сред

Среда	Кинематическая вязкость v , м2/с	Температуропроводность X , м2/с	Коэффициент теплового расширения р , 1/К
Гептан	0,61 - 10-6	0,88 - 10 -7	1,24 - 10-3
Ртуть	1,14 - 10 -7	4,47 - 10-6	0,18 - 10-3
Воздух	1,43 - 10-5	2,11 - 10-5	3,67 - 10-3
Керосин	1,82 - 10-6	0,70 - 10-7	0,96 - 10-3

• 4.    Карта режимов всплытия

На горизонтальных гранях полости поддерживалась постоянная температура Э ₀ = 20 °C. В начальный момент времени температура жидкости принималась равной температуре стенок. В процессе расчетов менялась только температура нагревателя Э . Таким образом, на нижней границе устанавливался П -образный профиль температуры. Для выявления зависимости различных характеристик плюма от свойств среды, соотношения сторон полости, мощности и размеров нагревателя в ходе расчетов отслеживалась эволюция температурного и вязкого пограничных слоев его ножки. Далее будем придерживаться следующих обозначений: 5 V , 5 T — соответственно ширина вязкого и температурного пограничных слоев.

В первую очередь получим независимую от результатов прямых 3D-расчетов оценку скорости всплытия теплового плюма. В приближении малых скоростей в установившемся режиме архимедова сила компенсируется вязкостью, поэтому соответствующие слагаемые в уравнении Навье–Стокса (1) должны быть по порядку величины равны vЛ w ~ g р T (здесь w — вертикальная компонента скорости V ). Главное слагаемое в лапласиане скорости отвечает производной по поперечной координате ножки плюма, поэтому имеем v w /52 ~ g Р0 , где 5 V является по смыслу характерной полутолщиной ножки плюма, 0 — верхняя оценка для разности температур в поперечном сечении. В результате при 0 ~ 1 ° C для гептана получаем следующее значение скорости всплытия: w ~ g Р5 2 0/v ® 1 см/с, что хорошо согласуется по порядку величины с результатами прямого численного моделирования.

Выясним теперь зависимость от вертикальной координаты ширины пограничных слоев полей скорости и температуры в конвективной струе. В случае развитого плюма уравнения (1), (2) допускают стационарное решение для струйного течения внутри ножки. При оценке вклада каждого слагаемого в этих уравнениях для простоты ограничимся рассмотрением двумерного движения в плоскости широких граней полости: V( v, w, 0 ). Сначала оценим величину слагаемых в уравнении несжимаемости ду/дx + дw/ду = 0: у/5V ~ w/y . Таким образом, для всех четырех режимов движения плюма всегда справедливо соотношение у ~ 5Vw/y . По аналогии сопоставим стоящие рядом слагаемые в уравнении (1). Спроектируем уравнение Навье–Стокса на ось y и учтем только главные члены. Будем считать, что вязкая, инерционная и подъемная силы являются величинами одного порядка, то есть w2 /у ~ vw/52 , vw/52 ~ gP0. Исключая из этих уравнений вертикальную компоненту скорости, получаем для ширины вязкого пограничного слоя следующую степенную зависимость [2]: 5V ~ (v2у(^gв0)) . Отсюда следует, что толщина вязкого пограничного слоя конвективной струи должна увеличиваться по степенному закону ~ у1/4. Естественно, эта асимптотика справедлива только в случае, когда инерционное и вязкое слагаемые характеризуются одинаковым вкладом в уравнение движения.

Оценим величину температурного погранслоя в режиме умеренно быстрого конвективного движения внутри ножки плюма. Уравнение переноса тепла дает в главном порядке 5 _Vw 0 /( 5 T y ) ~ w ©/ у , w ©/ у ~ X0/5 T , где Θ — характерный вертикальный перепад температуры на расстоянии y от начала координат. Из первого соотношения следует пропорция 5 T 5 V ~ 6/© , которая интерпретируется физически просто для отношения толщины погранслоев в двух предельных случаях: 0/© » 1 (интенсивная конвекция) и 0/© « 1 (слабая конвекция). Вертикальная компонента скорости определяется формулой w ~ v у /5 V , в результате второе соотношение дает важную оценку 5 V (ЪT ~ Pr . В частном случае, при Pr ® 1, получаем 5 T ~ 5 V . Эти рассуждения будут использоваться в дальнейшем при анализе результатов полного трехмерного численного моделирования.

Чтобы продемонстрировать специфику различных режимов всплытия плюмов, выведем сечения полей температуры и скорости в плоскости ( x , y ) при z = d 2 . Вязко-теплопроводный режим определяется широкими пограничными слоями температуры и скорости. При этом у конвективного факела наблюдается толстая ножка с округлой шляпкой, а температурный профиль больше напоминает лампочку (Рис. 2, а ; гептан при ∆ϑ = 1 °C). Данный режим всплытия имеет место при небольшой разности температур нагревателя и верхнего охлаждающего теплообменника. Заметим, что именно такие плюмы имеют место при численном моделировании работы датчика инерционных ускорений [8–10], когда было справедливо приближение Хеле-Шоу.

При увеличении температуры нагревателя скорость всплытия плюма растет, и теплота начинает переноситься преимущественно конвективной струей ножки, то есть в зависимости от числа Прандтля может установиться невязко-теплопроводный (Рис. 2, б ; Pr = 0, 026 , ∆ϑ = 180 °C) или вязко-нетеплопроводный (Рис. 3, а ; Pr = 6,8 , ∆ϑ = 15 °C) режим. Для невязко-теплопроводного режима характерна температурная ножка, широкая у основания, которая на больших временах слегка пережимается у верхушки, образуя небольшую тепловую головку плюма. В случае вязко-нетеплопроводного плюма пограничный температурный слой ножки тонкий, а вязкий пограничный слой широкий. Температурное поле такой конвективной структуры имеет «грибообразную» форму с тонкой ножкой и широкой, раскрывающейся в процессе движения шляпкой.

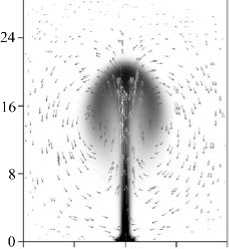
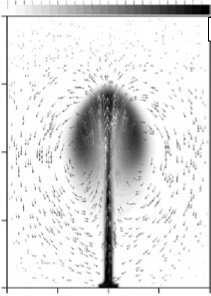
При еще больших температурах нагревателя возникает невязко-нетеплопроводный режим (Рис. 3, б ; Pr = 6,8 , ∆ϑ = 80 °C). Он характеризуется тонкими пограничными слоями скорости и температуры. Принадлежность к классу нетеплопроводных режимов отчетливо просматривается по виду температурного профиля ножки. У плюма наблюдается узкая ножка и крупная заостренная шляпка с двумя четко выраженными завихренностями, сильными на краях за счет еще большей скорости всплытия. Эти завихренности начинают заметно отставать от центральной части шляпки. По мере подъема также становится существенным нарушение симметрии конвективного факела относительно вертикали. Расчеты показывают, что при больших разностях температуры ножка плюма теряет устойчивость со временем и начинает изгибаться в плоскости широких граней.

20.00    20.04

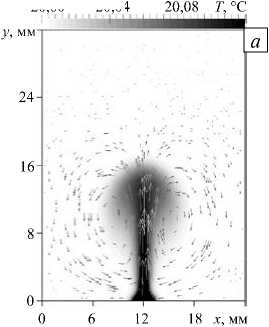
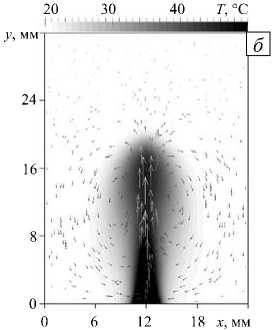
Рис. 2. Поля температуры и скорости в различных теплопроводных режимах: вязком ( а ) для Pr = 6,8 , ∆ϑ = 1 ° C; невязком ( б ) для Pr = 0,026 , ∆ϑ = 180 ° C

20,0

Г'

у, ММ--

у, мм

18 х, мм

Рис. 3. Поля скорости и температуры в различных нетеплопроводных режимах для Pr = 6,8 : вязком ( а ) при Дд = 15 ° C; невязком ( б ) при Дд = 80 ° C

На рисунке 3 можно видеть, что у плюмов в области шляпки есть локальный максимум температуры, который существует на протяжении всего времени всплытия (с момента его образования до сближения с верхней границей). По зависимости координаты этого максимума от времени можно судить о скорости его всплытия [17]. Расчеты показывают, что сначала скорость всплытия плюма увеличивается, затем становится постоянной, и наконец, по мере приближения к верхнему теплообменнику движение плюма замедляется.

Наиболее отчетливо различие в природе плюмов проявляется при анализе толщины пограничных слоев. Конечность размеров нагревателя и наличие боковых граней полости приводят к нарушению стандартных закономерностей в скорости расширения струи. Тем не менее, для достаточно малых размеров термоэлемента, путем экстраполяции линии пограничных слоев внутрь ножки плюма можно выделить точку над нагревателем, которая могла бы играть роль эффективного точечного источника тепла (Рис. 1). В результате графики зависимости ширины пограничных слоев от вертикальной координаты, как и раньше, можно представить в степенном виде: 5 T ~ a 1 ( у + b , ) “ , 5 V ~ a 2 ( у + b 2 )^р . Параметры Ь 1 и b ₂ отвечают за сдвиг эффективного точечного источника тепла вверх по оси у ; здесь а ив — константы, вычисляемые в процессе обработки массивов данных. Несколько характерных зависимостей толщины температурного и вязкого пограничных слоев от высоты представлено на рисунке 4 для гептана при разных температурах нагревателя. Значения степеней а и р показывают, что кривые 1 соответствуют вязко-теплопроводному ( а , в >  0,25), а кривые 2 и 3 — вязко-нетеплопроводному ( р >  0,25 > а ) режиму.

Хотя степенные законы становятся несколько другими при изменении размеров нагревателя l и ширины слоя d , по-прежнему с определенной точностью можно считать, что степень 1 4, отвечающая за скорость роста пограничных слоев в зависимости от вертикальной координаты, позволяет разграничивать различные режимы всплытия. Для ширины нагревателя 2 мм и толщины слоя 4 мм при высоте полости 24 мм систематизация плюмов по определенным качественным признакам дает на карте режимов (Рис. 5) результаты, аналогичные полученным в ходе двумерного численного моделирования [7]. Число Рэлея по вертикальной оси

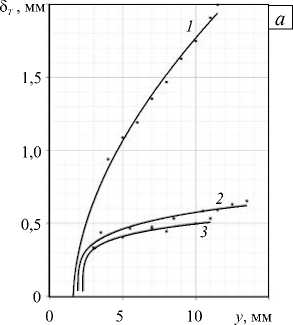
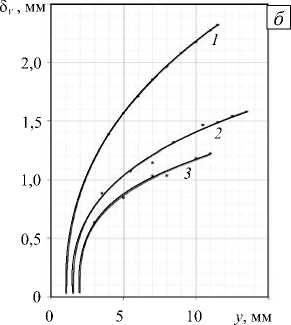
Рис. 4. Ширина пограничных слоев в зависимости от вертикальной координаты; температурный погранслой ( а ) при различных степенях а : 0,56 (кривая 1 ), 0,22 ( 2 ), 0,18 ( 3 ); вязкий погранслой ( б ) при различных степенях р : 0,40 (кривая 1 ), 0,34 ( 2 ), 0,31 ( 3 )

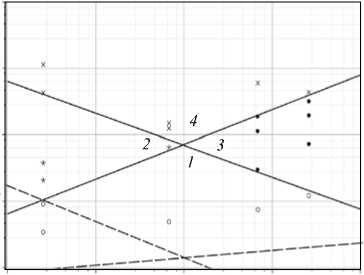
Рис. 5. Карта режимов; 1 – вязко-теплопроводный, 2 – невязко-теплопроводный, 3 – вязко-нетеплопроводный, 4 – невязко-нетеплопроводный; штриховые линии – аналогичные границы плоских режимов, взятые из работы [7]

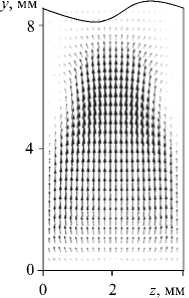
Рис. 6. Поле скорости в поперечном сечении при x = L/ 2

вычислялось через высоту полости: Ra = g в AH ⁴/(vx) , где A = ЛЭ/ H — характерный вертикальный градиент температуры. Представленная на рисунке 5 карта режимов построена по той же методике и приблизительно по такому же количеству расчетных точек, что и для двумерных плюмов. Однако для тонкой полости карта режимов сильно отличается в количественном отношении от аналогичной диаграммы, представленной в [7]. Интенсивное вязкое трение о широкие вертикальные грани приводит к тому, что границы режимов для тонкого слоя закономерно лежат существенно выше аналогичных линий, соответствующих двумерному численному моделированию. Иными словами, чтобы в полости типа ячейки Хеле-Шоу создать режимы нетеплопроводного типа, необходимы более высокие разности температур.

Помимо картины течения в плоскости ( x , y ), отраженной на рисунках 2, 3, значение имеет и распределение скоростей в сечении ( x , z ). На рисунке 6 представлено поле скоростей в поперечном широким граням сечении в нижней четверти слоя на начальной стадии формирования конвективной струи. Сечение выбрано на оси симметрии плюма. Видно, что z -компонента невелика, однако она все-таки сопоставима с наибольшей по величине вертикальной компонентой скорости. Расчеты показывают, что основной эффект, связанный с отсутствием двумерности в течении, заключается в замедлении движения плюма в 1,5–3 раза в зависимости от режима его всплытия.

• 5.    Взаимодействие плюмов

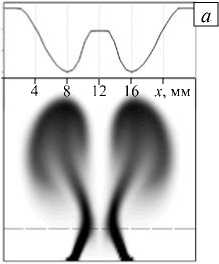
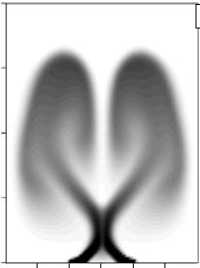
Синхронное всплытие плюмов, образующихся при наличии нескольких сосредоточенных источников тепла, экспериментально рассмотрено в [5, 6]. Если одинаковые нагреватели находятся недалеко друг от друга, в процессе всплытия наблюдается взаимодействие плюмов. Показано, что это взаимодействие становится существенным для развитых плюмов с достаточно длинной ножкой и ярко выраженными тонкими температурным и вязким погранслоями. В экспериментах расстояние между нагревателями превышало их собственные размеры в 2–4 раза. В некоторый момент времени происходил излом ножек и проявлялось их взаимное притяжение друг к другу (Рис. 7). При этом изогнувшиеся струи ножек могли практически соприкасаться на определенной высоте, но все же не сливались. В свою очередь шляпки плюмов объединялись, образуя единый нетривиальный по форме тепловой фронт.

р’, Па-10"3

4   8 12 16 х, мм

а

V. мм

б

4   8   12 16   ,v, мм

т

21,4

21,2

20,8

20,4

20,0

Рис. 7. Поля температуры двух взаимодействующих плюмов в гептане ( ЛЭ = 60 ° C) в разные моменты времени: t i <  1 2 ; на фрагменте ( а ) приведен график зависимости конвективной добавки к полному давлению на высоте излома ножек

Для более глубокого физического понимания обнаруженных в опытах эффектов и их количественного описания выполнено теоретическое исследование в виде прямого численного моделирования. В реализованной серии расчетов полагалось, что полость нагревается снизу двумя линейными нагревателями размером l = 1 мм, отстоящими друг от друга на расстоянии 6 мм. Вычисления проведены для гептана при разности температур ЛЭ = 60 °C. В натурном эксперименте в полости размерами порядка нескольких сантиметров весьма проблематично напрямую измерить давление в разных точках полости. В расчетах эта трудность преодолевается за счет использования пакета OpenFOAM. График поведения конвективной добавки p ‘ к давлению вдоль горизонтальной линии, проходящей через середину боковых граней на высоте излома ножек, однозначно показывает (Рис. 7, а ), что в области между плюмами, в соответствии с законом Бернулли, давление заметно ниже, чем снаружи. В результате ножки двух близлежащих плюмов изгибаются по направлению друг к другу, что соответствует притяжению конвективных струй.

• 6.    Заключение

Проведенное прямое численное моделирование тепловых плюмов в тонком вертикальном слое показывает, что систематизация их всплытия с делением на четыре типа (вязко-теплопроводный, вязко-нетеплопроводный, невязко-теплопроводный и невязко-нетеплопроводный) имеет глубокий физический смысл. А именно: классификация, разработанная ранее для двумерной модели, «работает» и в случае щелевых зазоров, но при этом наблюдаются отличия, связанные с присутствием трения на широких гранях полости.

В трехмерной постановке выполнен расчет карты режимов, позволяющей установить области параметров, при которых существуют указанные типы всплытия плюмов. Несмотря на существенное взаимодействие конвективного факела с широкими гранями и потерю в вертикальном слое свойства двухмерности, обсуждаемая градация остается справедливой и отражает основные причинно-следственные связи, лежащие в основе рассматриваемых конвективных явлений. Расчет взаимодействия плюмов в процессе всплытия дополняет общую характеристику их природы. Показано, что в ходе синхронного всплытия ножки плюмов, отстоящие друг от друга на расстоянии порядка размеров нагревателей, притягиваются.