Резонансное множество многочлена и проблема формальной устойчивости

DOI:

Во многих прикладных задачах возникает ситуация, когда для некоторого многочлена /(ж) необходимо сформулировать условия на его коэффициенты, при выполнении которых этот многочлен имеет соизмеримые корни. Так, например, условие целочисленной соизмеримости (кратности) корней характеристического многочлена матрицы линейной части уравнений движения вблизи положения равновесия выделяет в пространстве коэффициентов многочлена (или параметров уравнений движения) многообразия, на которых имеется резонанс между собственными частотами колебаний. Случай, когда многочлен /(ж) имеет корень кратности к >  1, является частным случаем описанной выше ситуации.

Эта статья продолжает исследования автора [4–6] по описанию структуры и построению параметрического представления дискриминантного множества Т> (/ _п ) многочлена

/ „ (ж) *= ж ” + а1ж ” ¹ + а ₂ ж^{п 2} + • • • + а_п

п-й степени с вещественными коэффициентами. Вещественное п-мерное пространство П = R ” его коэффициентов а1,а ₂ ,... а _п , как и ранее, назовем пространством коэффициентов многочлена (1).

Определение 1. Пару корней ti, t , , г, j = 1,... ,п, г = j, многочлена (1) назовем р : q-соизмеримой, если t _i : t j = р : q.

Замечание 1. Здесь и далее предполагаем, что р Е Z \{0}, q Е N , то есть исключаем случай, когда один из корней t _i или t j равен нулю, поскольку нулевой корень соизмерим с любым другим корнем.

Замечание 2. Если у многочлена (1) есть пара р : q-соизмеримых корней, то есть и пара q : р-соизмеримых корней. Следовательно, далее предполагаем, что коэффициент соизмеримости р : q удовлетворяет условию | р/q | >  1.

Определение 2. Резонансным множеством ^(/ _га ) многочлена / _п (ж) назовем множество всех точек пространства коэффициентов П, в которых / _п (ж) имеет хотя бы пару соизмеримых корней. Для фиксированного коэффициента соизмеримости, задаваемого рациональным числом р/q Е Q , соответствующее резонансное множество обозначим через ^_p;q (/ „ ), то есть

Р _р . _ч (/ ” ) = { Р Е П: 3 г,j Е 1,...,п, t i : t , = р : q}. (2)

Очевидно, что дискриминантное множество Т> (/ _п ), то есть множество, на котором многочлен (1) имеет кратные корни, является частным случаем резонансного множества (2) для значения коэффициента соизмеримости р : q = 1.

Цель данной статьи — разработать конструктивный алгоритм вычисления параметрического представления всех компонент резонансного множества ^ _{р ; р} (/ „ ) приведенного вещественного многочлена / „ (ж).

Статья состоит из введения, трех разделов и заключения. В разделе 1 формулируется условие на коэффициенты существования соизмеримых корней многочлена (1) в терминах обобщенных субдискриминантов, которые с точностью до множителя суть субрезультанты пары многочленов /п(рж) и /п^ж). В разделе 2 дано описание иерархической структуры резонансного множества ^р;р(/„), указана связь этой структуры с задачей разбиения натурального числа п, описан алгоритм построения параметрического представления компонент этого множества и дано описание программной библиотеки для системы компьютерной алгебры Maple. В заключительном разделе 3 приведено описание резонансного множества кубического многочлена, а также дано приложение полученных результатов к решению проблемы формальной устойчивости положения равновесия многопараметрической системы Гамильтона с тремя степенями свободы.

Предварительные результаты статьи докладывались на международных конференциях: Polynomial Computer Algebra-2016, г. Санкт-Петербург, 18–23 апреля 2016 г., III Международная конференция «Геометрический анализ и его приложения», г. Волгоград, 30 мая – 3 июня 2016 г. и опубликованы в препринте автора [7].

1.    Условие р : q-соизмеримости корней многочлена fn(oc)

Пусть многочлен / _п (х) имеет пару р : q-соизмеримых корней. Это эквивалентно тому, что два многочлена / _п (рх) и /_п^х) имеют общий корень, или, другими словами, Res _x (/ _n (рх), / _n (qx)) = 0, где Res ^ (д, К) — результант многочленов д(х) и К(х), вычисленный относительно переменной х.

Определение 3. Пусть n                 т

д(х)=П(х - t i ), К(х) = Ц( х - U i ) i =1                        i =1

суть два приведенных многочлена степени п и m соответственно. Тогда их результант относительно переменной х вычисляется по формуле n т Res,(g,K) = niI(ti - U). i=i j=i

Поскольку при р = q = 1 многочлены / _п (рх) и / _n (qx) имеют п общих корней, то результант Res _ж (/ _n (px),/ _n (qx)) делится на множитель (р — q) ⁿ . В силу замечания 1, результант Res ^ (/ _п (рх),/ _n (qx)) делится на свободный член a _n многочлена (1). Таким образом, указанный выше результант представим в виде

Res$(/п(рх), /n(qx)) = ап(р — q)n GDp;(/(/), где GDp;p(/n) — введенный в [1; 3] обобщенный дискриминант многочлена /п(х). Термин «обобщенный дискриминант» выбран в связи с тем, что при стремлении коэффициента соизмеримости р : q ^ 1, значение обобщенного дискриминанта GDp;q(/n) стремится к значению дискриминанта D(/n) многочлена (1).

У многочлена (1) может быть не одна пара р : q-соизмеримых корней. Для полного исследования структуры р : q-соизмеримых корней введем несколько вспомогательных понятий.

Определение 4. Цепочкой Ch^(t j ) p : q -соизмеримых корней длины к (кратко цепочкой корней ) назовем отрезок длины к геометрической прогрессии с основанием t _i и знаменателем p/q, каждый член которой является корнем этого же многочлена. Основание прогрессии t _i назовем порождающим корнем соответствующей цепочки.

Замечание 3. Для того чтобы коэффициенты полиномиальных объектов (многочленов, субрезультантов, параметрических представлений компонентов резонансного множества ^._{p ; q} (f _n ) и др.) были представлены в виде многочленов, а не рациональных функций от чисел р и q, будем в цепочке корней длины к в определении 4 использовать величину q ^{k -1}t _i в качестве порождающего корня.

Резонансное множество ^ _{p ; q} (f _n ) для каждого фиксированного коэффициента соизмеримости р : q состоит из конечного числа многообразий V / , на каждом из которых многочлен f _n (x) имеет I цепочек корней Ch p^fcq ⁾ (t _i ) с различными порождающими корнями t _i , г = 1,... ,1. Суммарная длина этих цепочек корней равна степени п многочлена

Для описания каждого из многообразий V/ нужно знать структуру корней наибольшего общего делителя многочленов fn(px) и fn(qx), то есть многочлена fp;q (x) d=f gcd( fn(px), fn(qx)).                                (3)

Пусть d = deg f _{p ; q} > 0, тогда корни многочлена f _{p ; q} (x) дают информацию о кратных корнях исходного многочлена (1): каждой цепочке корней Chp^tJ многочлена f _{p ; q} (x) соответствует цепочка корней Ch p^^ ¹ ) (t _i ) многочлена f _n (x). Структуру корней многочлена удобно определить с помощью субрезультантов [12; 17] пары многочленов f _n (px) и f n (qx).

Известно много методов вычисления результанта пары многочленов. Их обзор дан, например, в [4; 12]. Здесь ограничимся методом Сильвестра.

Определение 5. Матрицей Сильвестра Sylv(f,g) двух многочленов f(x) и g(x), для которых п = deg f (x) и m = degg(x), называется квадратная матрица размера (п + т), строки которой суть векторы, составленные из коэффициентов многочленов xm-1f (x), xm-2f (x),..., xf (x), f (x), g(x), xg(x),..., xn-2g(x), xn-1g(x)

в базисе x ^{n + m - 1} ,..., x, 1.

Определение к-го субрезультанта пары многочленов f (x) и g(x) дадим с помощью иннора [10] матрицы Sylv (f,g).

Определение 6. Пусть M _n — квадратная матрица размера п х п. Тогда матрица M _n- fe , к <  [п/2], полученная вычеркиванием по к крайних строк и столбцов с обеих сторон исходной матрицы M _n , называется ее к-м иннором .

Определение 7. к-м субрезультантом Res^(k)(f,g) многочленов f (x) и g(x) называется определитель к-го иннора матрицы Сильвестра Sylv (f, g).

Запишем матрицу Сильвестра Sylv (f _n (px), f _n (qx)) размера 2п х 2п для многочленов f n (px) и f n (qx):

SУlv (f n (Pх), f n (дх)) =
	/ р П	п1 ар       • • •	„2 а п -2р	а п -1р	а п	0     •••	0	0 ^
	0 .	р П       • • • ..	а п -зр .	ап-2р .	а п -1р .	а п • • • ..	0 .	0 .
=	. . 0 0 .	.. .. 0          • • • 0     ••• ..	. . р п д п .	. . а 1 рп - 1 а 1 д п -1 .	. . а 2 рп-2 а2д п -2 .	.. .. азр п 3 • • • а з д п 3 ••• ..	. . а п -1р а п -1д .	. . а п а п .	. (4)
	. . 0	.. .. д п        • • •	. . а п -зЧ	. . 2 а п -2д2	. . а п -1д	.. . . а п • • •	. . 0	. . 0
	\дп	П 1 ^ 1 д         •••	а п -2д2	а п -1д	а п	0     •••	0	0

Матрица (4) имеет п — 1 нетривиальный иннор. Очевидно, что в силу ее структуры каждый из определителей этих инноров, то есть соответствующий субрезультант, раскладывается на три множителя. Можно показать, что для к-го субрезультанта многочленов f _п (рх) и f _п (дх) имеет место следующее разложение:

Res <‘> (f „ (px),f „ (дх)) = (р — д ' (рд) ^к<" ^{- к )} GD*(f „ ).               (5)

Определение 8. Назовем к -м обобщенным субдискриминантом GD^(f _n ) многочлена / _п (х) для коэффициента соизмеримости р : д третий нетривиальный множитель в формуле (5) .

Пусть многочлен fn(x) имеет цепочку р : д-соизмеримых корней длины к с порождающим корнем t, то есть в силу замечания 3 он имеет вид к-1

f _n (x) = п(х) ^ ( х — р^гд ^{к- 1-}Ч) .

2=0

Здесь многочлен и(х) степени п — к не имеет р : д-соизмеримых с t корней. Тогда к-2

f n (pх) = п(рх) рх — g ^{к - 1} t ) р ^{к - 1} ^ ( х — р^гд^{к 2} ' t ) ,

2 = 0

к - 2

f n (gх) = п(дх) ( дх — р ^{к - 1} 1 ) д ^{к - 1} ^ ( х — р^г д ^{к 2} ' t ) .

2=0

Следовательно, многочлен f _{p ; q} из формулы (3) имеет цепочку р : д-соизмеримых корней длины к — 1 с порождающим корнем g ^{k - 2} t.

В силу приведенных выше рассуждений, а также теоремы 3.3 из [12], имеет место следующая теорема.

Теорема 1. Для того чтобы deg f _p-_q (х) = d , необходимо и достаточно, чтобы в последовательности г -х обобщенных субдискриминантов GD^(f _n ) первым отличным от нуля обобщенным субдискриминантом был субдискриминант GD^(f _n ) с номером d .

Введем полиномиальные идеалы 2^(/ _n ), состоящие из первых / обобщенных субдискриминантов GD« (/ „ ):

I® (/ n ) = { go® (/,.),* = 0,...,/- 1 } .

Тогда согласно теореме 1 нули идеала Z ’¹, (/ _n ) образуют множество, на котором многочлен / _п (х) имеет в точности к <  п различных цепочек р : q-соизмеримых корней.

2.    Параметризация резонансного множества ^.p:q(/„)

Множество ^._p;q (/ _n ) состоит из алгебраических многообразий V ; размерностей /, 1 6 / 6 п — 1. Общее число этих многообразий, а также число различных многообразий V _l , имеющих фиксированную размерность /, зависит от числа разбиений р(п) степени п многочлена / _п (ж).

2.1.    Число компонент резонансного множества ^p:q(fn)

Напомним здесь основные определения, связанные с разбиением натуральных чисел; подробнее см. [4; 13; 16; 20].

Определение 9. Разбиением Л натурального числа п называется всякая конечная неубывающая последовательность натуральных чисел Л 1 6 Л ₂ 6 • • • 6 Л _к , для которой к

£ лг = п.

i =1

Каждое из разбиений запишем в виде Л = [1 ⁿ 1 2 ⁿ 2 3 ⁿ 3 ... ], где п _г — число повторений слагаемого г в разбиении, то есть f^ гп _г = п.

Основные числовые функции, связанные с множеством разбиений числа п, следующие:

• •    Функция р(п) задается числом всех разбиений числа п (последовательность A000041 в [20]).

• •    Функция р_к(п) задается числом всех разбиений п на к слагаемых.

• •    Функция q(п) задается числом всех разбиений п на различные слагаемыe (последовательность A000009 в [20]).

• •    Функция q_k(п) задается числом всех разбиений п на к различных слагаемых.

2.2.    Иерархическая структура компонент множества ^р:(?(./',,)

Очевидно, что р(п) = ^f р к (п) и q(п) = ^f q k (п).

к =1                  к =1

Рассмотрим разбиение Л = [1n1 2n2 .. .гп... ] натурального числа п. Величина г в разбиении Л задает длину цепочки р : q-соизмеримых корней для соответствующего порождающего корня ti, а пг — число различных порождающих корней, задающих цепочку корней длины г. Тогда / = i^i пг есть число различных порождающих корней многочлена /п(х) для коэффициента соизмеримости р/q и ^г гпг = п. Любое разбиение Л числа п определяет некоторую структуру р : q-соизмеримых корней многочлена, и этой структуре соответствует в пространстве коэффициентов П некоторое алгебраическое многообразие V/, г = 1,... ,р1(п), размерности / по числу различных порождающих корней ti. Число таких многообразий размерности I равно pi(п), а общее число многообразий всех возможных размерностей равно р(п) — 1, поскольку разбиению [1п] соответствует ситуация, когда все порождающие корни многочлена (1) задают цепочки корней длины 1, то есть среди всех корней многочлена /п(х) нет ни одной пары р : q-соизмеримых корней.

Замечание 4. В силу того что исходный многочлен (1) вещественный, комплексные корни его образуют пары — сам комплексный корень t ^ и ему комплексно сопряженный 1 _г . Если порождающий комплексный корень t ^ задает цепочку корней длины к, то и сопряженный ему корень 1 _г задает цепочку корней такой же длины, в которой каждый корень является комплексно сопряженным соответствующему корню из цепочки корней, задаваемых корнем t ^ . Значит, в разбиении Л , которое соответствует такой структуре корней, будет два равных слагаемых. Следовательно, на алгебраическом многообразии V _i С П размерности I многочлен / _п (х) имеет только вещественные корни, если соответствующее ему разбиение числа п есть разбиение, состоящее из I различных слагаемых. Число таких разбиений для фиксированного I есть значение функции q _i (п), а общее число компонент резонансного множества ^ _{р : ц} (/ _п ), на которых все корни вещественны, задается функцией q(п).

Рассмотрим разбиение [п1], которое соответствует случаю, когда имеется единственная цепочка корней длины п, задаваемая порождающим (очевидно вещественным) корнем qn—1t1. Тогда многочлен /п(х) имеет вид п— 1

/ п (х; ti) = ^ [ х — р ⁵ q^{n -1—l} t i ] .                             (6)

3 =0

Здесь запись / _п (х; t1) означает, что все корни многочлена (1) зависят от параметра t1. В этом случае его коэффициенты а _г выражаются через элементарные симметрические многочлены [13; 15] о _г (х ₁ ,х ₂ ,...,х _п ), вычисленные на корнях вида р ⁵ q ^{n— 1—: i} t1, i = 0,..., п — 1, соответствующей цепочки корней.

а ^ = (—1) ^г ^ ( q ^{n —} 1 t 1 ,pq ^{n — 2} t 1 ,... ,p ^{n —} 1 t 1 ) , г = 1,...,п.                 (7)

В силу однородности симметрических многочленов о _г , коэффициенты а _г являются степенными функциями степени г параметра t1 .

Согласно теореме 1 в этом случае deg f _{p : q} (х) = п — 1, то есть в последовательности обобщенных субдискриминантов GD^(/ _п ), г = 0,..., п — 1, первый отличный от нуля обобщенный субдискриминант есть GD (n - ¹⁾ (/ _п )• Следовательно, формулы (7) задают параметрическое представление нулей идеала 2^"" 1) . Эти нули представляют собой одномерное многообразие (кривую) V i¹) в пространстве коэффициентов П. Эта кривая не имеет особых точек, поскольку в силу ее параметрического представления (7) а _г ~ t[ и, следовательно, производные da ^ /dt1 одновременно в ноль не обращаются.

Рассмотрим следующую конструкцию. Выберем на кривой V^1) пару точек, соответствующих значениям параметра t1 = 0 и (p/q)—1t1, и проведем через них прямую. Покажем, что на этой прямой многочлен /п(х) имеет одну цепочку р : q-соизмеримых корней длины п — 1 и одну цепочку корней длины 1, то есть простой корень. Действительно, рассмотрим вспомогательный многочлен

g(x; 4 1 ,«) = / „ (x; 4 1 ) + «^iM- A(^x; (^p/q> ^- М .             (8)

Тогда с учетом формулы (6) получим, что g(x; 41,«) =

x

—

(+ «£

—

q

■

p

n — 2

П1 Х

3=G

— p ³ q^{n 2 3} q4 1] .

Выбирая

Р (4 2 — p ^{n —} 1 4 1 )

« = --------------, pn — qn n—2

получим, что g(x; 41,42) = (x — 42) П [x — p3qn—2—3q41], то есть многочлен g(x; 41,42) 3=g имеет один простой корень 42 и цепочку корней Ch^ 1)(q41). Очевидно, что структура корней в этом случае соответствует разбиению [11(п — 1)1].

Таким образом, коэффициенты вспомогательного многочлена (8) задают в пространстве П многообразие V ₂ , представляющее собой линейчатую поверхность. Оно образовано секущими, которые пересекают кривую V 1 в точках, соответствующих таким значениям 4 11) и 4® параметра 4 1 , что 4 12) /4 11) = p/q. При p/q ^ 1 эта линейчатая поверхность превращается в касательную развертывающую поверхность, параметризация которой задается формулой (3.6) из [4].

Описанную выше процедуру теперь можно повторить для многообразия V ₂ и получить параметрическое представление части многообразия V ₃ , на котором имеется цепочка корней длины п — 2 и пара простых корней, то есть ему соответствует разбиение [1 ² (п — 2) ¹ ]. Продолжая последовательно эту процедуру, в итоге придем к параметрическому представлению многообразия V _{n— 1} наибольшей размерности. На нем имеется одна цепочка p : q-соизмеримых корней длины 2, а остальные корни простые, то есть ему соответствует разбиение [1 ^{n —} 2 2 ¹ ]. Очевидно, что в силу замечания 4 полученная параметризация описывает только ту часть многообразия V i , 3 6 I <  п, на котором все корни многочлена (1) вещественные.

2.3.    Алгоритм построения параметризации многообразий Vi

Рассмотрим конструктивную процедуру вычисления параметрического представления многообразий V для всех значений I = 1,... ,п — 1 и г = 1,... ,p _i (n).

Теорема 2. Пусть в пространстве П имеется многообразие V , dim V = I , на котором многочлен (1) имеет I различных цепочек p : q -соизмеримых корней, причем цепочка корней Ch ^^m) (4 ₁ ) имеет длину т >  1 . Другие корни I — 1 цепочки не являются p : q -соизмеримыми со всеми корнями цепочки Ch ^™) (4 ₁ ) .

Пусть ri (41,..., 4i) — параметризация многообразия V, тогда формула ri (41,..., 4i, 4i+1) = ri (41,..., 4i) +

^{+         — p} m ^) ^[ r i ⁽⁴ 1 , ..., ⁴ i ) ^— r i ⁽⁽q/p⁾⁴ 1 , ..., ⁴ i ^{)] (9)}

⁴ 1 ^{(p — q} )

задает параметризацию части многообразия V _{i +i} , на котором имеется цепочка корней Ch^ ^{- i} ) (qt _i ) , простой корень t _{i +i} , а остальные цепочки корней такие же, как на исходном многообразии И .

Доказательство. В силу условия теоремы многочлен / _п (х) на многообразии И факторизуется следующим образом:

ш, ti,...,t i )=u(x) П [ 1 - Р q^ ^— t i ] ,                (10)

1=0

где многочлен и(х) не имеет корней р : q-соизмеримых c корнями цепочки, порожденной t _i . Рассмотрим вспомогательный многочлен д(х; ti,... ,t _i ,v), коэффициенты которого непрерывно зависят от параметров t _i , . . . ,t _i ,v следующим образом

/ ,        , х , , . .х . / п ^(х; ^t i ^,...^,t i ) - ^fn ^(x;(p/qV^ti^,...^,ti)

д(х; ti,...,t i ,х) = / п (х; ti,...,t i ) + v--------------------------------------------------.

^t i

Подставляя выражение для / _п (х) из формулы (10), получим

д(х;t i ,... ,t i ,v) = и(х)

- ( р- i t i + vP"!^ у

X

X П ( х - Р q ^m- -³qti ) . 1=0

Полагая теперь

v =

Р (t i+i - P ^{m i}ti)

P

m

- q ^m

получаем m—2

• д(х; t i ,... ,t i+i ) = и(х; t₂, ... ,t l )(x - t i+i ) П ( 1 - P ¹ ч " '2 -qti) •          (ⁿ)

1=0

Таким образом, многочлен д(х; t _i ,...,t _{i +i} ) имеет цепочку корней длины т - 1 с порождающим qt _i , один простой корень t _{i +i} и остальные п - т корней такие же, как у многочлена / _п (х). Следовательно, формула (9) параметризует ту часть многообразия V _{i +i} , на которой многочлен / _п (х) имеет описанную выше структуру корней.

Замечание 5. Если в формуле (11) заменить параметр t _i на t _i /q, то получим параметризацию части многообразия V _{i +i} в виде, задаваемом формулой (10).

Замечание 6. Пусть один из корней, например u _i , многочлена и(х) в условии теоремы 2 простой, то есть и(х) = (х - ы₁ ) й ( х ) . Тогда на части многообразия V _{i +i} исходный многочлен имеет пару комплексно-сопряженных корней. Чтобы получить параметрическое представление этой части многообразия V _{i +i} , следует сделать такую замену параметров:

t i +i ^ V i + %V2, U i ^ V i - %V2.

Эта замена параметров приведет к тому, что многочлен / _п (х) на части многообразия V z+₁ , где есть пара комплексно-сопряженных корней, можно представить в виде

/ „ (х) = й(х) ( (х - « 1 ) 2 + « ₂ ² ) П [ 1 - Р^-Х ] .             (12)

3 =0

Если поменять знак перед слагаемым « 2 в правой части формулы (12), то получим факторизацию многочлена / _п (х) на той части многообразия V _{z +1} , где имеется пара простых вещественных корней « ₁ ± « ₂ . Таким образом, для получения параметризации всего многообразия V _{z +1} следует использовать подстановку

• ^t z+1 ^ « 1 + V« 2 , М 1 ^ « 1 ^- V« 2 ,                      ⁽¹³⁾

которая в итоге позволит записать многочлен /п(х) на всем многообразии Vz+1 в виде т—2

f n (x) = ( (х - « 1 ) ² + « 2 ) й(х) П [ 1 - Рq ^{m —2—3} 1 1 ] .      □

• 3 =0

Так же, как это было сделано в [4], введем три основные операции, которые позволят последовательно перейти от параметрического представления одномерного многообразия V ₁ к параметризации всех других компонентов резонансного множества ^ _{р ; ц} (/ „ ):

• 1)    Назовем операцию перехода от многообразия V _z к многообразию V _{z +1} в теореме 2 «ПОДЪЕМ» . Эта операция позволяет перейти к многообразию, размерность которого на единицу больше размерности исходного. Если на нем многочлен (1) имеет только вещественные корни, то получим полную параметризацию этого многообразия, если имеются комплексные корни, то применим следующую операцию.

• 2)    Операцию, основанную на замене (13) в замечании 6, назовем «ПРОДОЛЖЕНИЕ» . Эта операция позволяет получить параметризацию всего многообразия V _{z +1} , полученного в результате операции «ПОДЪЕМ», в случае, когда на последнем имеются комплексно-сопряженные корни.

• 3)    Если на многообразии V _{z +1} многочлен / _п (х) имеет пару различных цепочек корней одинаковой длины к, то можно перейти к многообразию V z , на котором имеется цепочка корней удвоенной длины 2к. Такую операцию назовем «СПУСК» . Если после этого перехода на многообразии V _z имеется пара корней одинаковой кратности, то для них следует выполнить процедуру «ПРОДОЛЖЕНИЕ».

Опишем алгоритм получения параметрического представления алгебраических многообразий V/, I = 1,... ,п - 1, г = 1,..., p _z (п), составляющих резонансное множество ^■p : q ^(/ п ^):

• 1)    Вначале строим параметрическое представление одномерного многообразия V₁по формулам (7).

• 2)    Применяем операцию «ПОДЪЕМ», получаем параметризацию многообразия V1, соответствующего разбиению [1¹(п - 1)¹].

• 3)    Вновь применяем операцию «ПОДЪЕМ» и получаем параметризацию многообразия V1, которое соответствует разбиению [1²(п - 2)¹]. Поскольку на этом многообразии имеется пара простых корней, то следует применить операцию «ПРОДОЛЖЕНИЕ». В итоге получаем полную параметризацию многообразия Vj.

• 4)    Применяя к последней параметризации операцию «СПУСК», получаем параметрическое представление многообразия V2, на котором корни многочлена /_п(х) соответствуют разбиению [21(n — 2)¹].

• 5)    Последовательно комбинируя операции «ПОДЪЕМ», «ПРОДОЛЖЕНИЕ» и «СПУСК», получим параметрическое представление всех компонент резонансного множества R_p:p(/„).

2.4. Программная реализация

Утверждение 1. Резонансное множество R_{p : q} (/ „ ) вещественного многочлена / _п (х) для фиксированного коэффициента соизмеримости p : q допускает полиномиальную параметризацию каждого из алгебраических многообразий Vi, составляющих резонансное множество.

Для организации вычисления резонансного множества R _{p : p} (/ _п ) в системе компьютерной алгебры Maple был реализован набор процедур, из которых скомпонована программная библиотека ResonanceSet . Библиотека расширяет возможности другой библиотеки SubDiscrim , ориентированной на работу с дискриминантным множеством многочлена Т> (/ _п ) и описанной в [4; 5].

В состав библиотеки вошли следующие процедуры:

• •    GDiscrim — для вычисления k-го обобщенного субдискриминанта GDP^/n) многочлена /_п(х) для фиксированного коэффициента соизмеримости p : q.

• •    MkFaml — для вычисления параметрического представления многообразия V₁.

• •    ProcUp — для реализации процедуры «ПОДЪЕМ» (см. п. 1 на с. 15).

• •    ProcCont — для реализации процедуры «ПРОДОЛЖЕНИЕ» (см. п. 2 на с. 15).

• •    ProcDown — для реализации процедуры «СПУСК» (см. п. 3 на с. 15).

3.    Резонансное множество кубики

Каждая из процедур реализована в двух вариантах. Первый вариант предназначен для вычислений при целом коэффициенте соизмеримости, второй — при рациональном.

В качестве примера работы алгоритма рассмотрим структуру резонансного множества кубического многочлена

• / ₃ = х³ + ° ₁ х² + ° ₂ х + ° ₃ .                           (14)

Кубика (14) имеет два обобщенных субдискриминанта

GD P ¹^) =pq° 1 ° 2 + (p ² + pq + q ² )° i ° 3 — (p + q) ² ° 2 ,

^GD P ?< ⁾ (^/ 3 ⁾ = ^{— [pq (p} + ^{q)] 2} ( ° 3 ° 3 + ° 3 ) + ^{(pq) 3} ° 1 ° 2 ^— ( ^{p 2} + ^pq + ^{q 2} ) ° ² +

+ pq (p ² + pq + q ²) (p ² + 4pq + q ²) ° i ° 2 0 3 .

Поскольку p(3) — 1 = 2 (см. с. 12), то резонансное множество ^р:р(/3) состоит из двух компонент

V 1 (/ з ) : {0 1 = — (p ² + pq + q²) t 1 , 0 2 = pq (p² + pq + q²) t1,

^o 3 = ^—(pqti)^3},

ТЛШ : {«1 = —(p + q)ti - t2, 02 = pqtl + (p + q)tit2, 03 = —pqt2t2 }, соответствующих разбиениям [31] и [1121]. Очевидно, что на многообразии V1(/3) нет комплексных корней, следовательно, V1(/3) С V2(/3).

Геометрически множество ^ _{р : р} (/ 3 ) представляет собой линейчатую поверхность (16) со скрученной кубикой (15) в качестве направляющей. Эта поверхность самопересе-кается по своей направляющей, которая, в свою очередь, является множеством особых точек поверхности Р ₂ . Множество ^ _{р : р} (/ 3 ) показано на рисунке 1. Заметим, что при p = q получим дискриминантную поверхность У(/ ₃ ) (см. раздел 4 в [4]), а при p = — q имеем св ро> (/ з ) = p ⁶ (o ₃ — о ₁ о ₂ ) ² , то есть поверхность V ₂ (/ ₃ ) есть гиперболический параболоид.

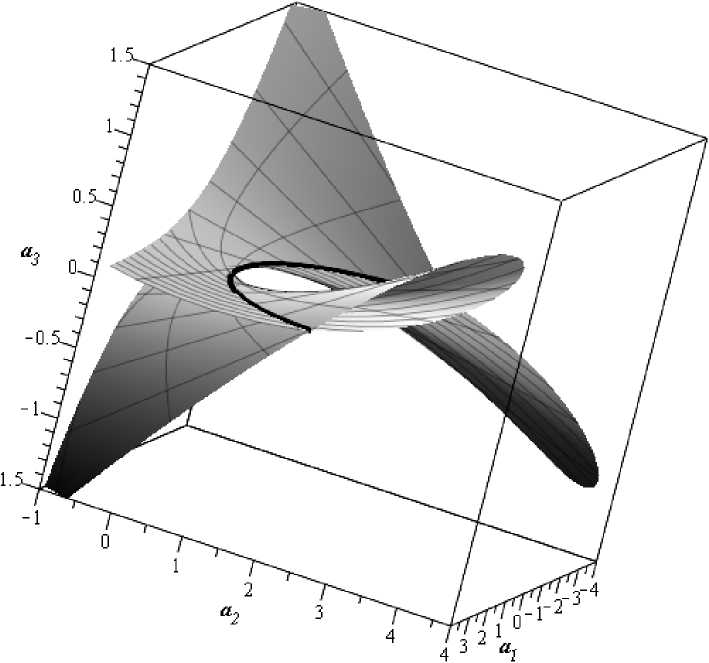
Рис. 1. Резонансное множество ^._р:д ( J ₃ ) для коэффициента соизмеримости р : q = 7. Выделена кривая (15), по которой поверхность (16) самопересекается

Дискриминантная поверхность У(/3) делит пространство коэффициентов П на две области с разным числом вещественных корней: в области П1 многочлен /3(ж) имеет три вещественных корня, в области П2 — один вещественный и пару комплексно-сопряженных корней. Поскольку на многообразии V2(/3) кубика (14) имеет только вещественные корни, то множество ^р:ц(/3) для любого значения коэффициента p : q = — 1 целиком содержится в области П1 и только может касаться дискриминантного множества £>(/3). Нетрудно видеть, что поверхности V2(/3) и У(/3) касаются друг друга вдоль пары кривых, на которых третий корень, не соизмеримый ни с одним из двух других корней, совпадает с одним из корней этой пары. В силу вышеизложенного, параметрическое представление кривых 01,2, по которым дискриминантная поверхность Р(/3) касается резонансной поверхности V2(/3), получается из (16) подстановками t2 = qt1 и t2 = pt1 соответственно:

0 1 : { a i = — (p + 2q)t i , 0 2 = q(2p + q)t1, a ₃ = — q^pt^ , (17) О : { a i = — (2p + q)ti, 0 2 = p(p + 2q)t 1 , a ₃ = — qp²!^ . (18)

3.1.    Приложение к проблеме формальной устойчивости положения равновесия

Рассмотрим подробнее ситуацию, возникающую при исследовании устойчивости положения равновесия некоторой многопараметрической системы Гамильтона с тремя степенями свободы.

Пусть в окрестности этого положения равновесия функция Гамильтона Н ( z ) может быть представлена в виде ∞

Н (z) = ^Hi(z), i=2

где z = (q, p), q и p — канонически сопряженные векторы координат и импульсов соответственно, а Hi (z) — однородная функция степени г от них. Как известно, в гамильтоновом случае характеристический многочлен /(Л) линеаризованной системы канонических уравнений z = JAz, где Лdef HessH2, (19)

является многочленом только от четных степеней Л . Здесь матрица J — симплектиче-ская единица. Тогда многочлен /( ц ) def /( ^ ), ц = Л ² , названный в [2] полухарактери-стическим , является приведенным кубическим многочленом (14).

В терминах полухарактеристического многочлена /( ц ) критерий устойчивости положения равновесия линеаризованной гамильтоновой системы (19) формулируется следующей теоремой.

Теорема 3 ([2]). Положение равновесия z = 0 линеаризованной гамильтоновой системы (19) устойчиво по Ляпунову тогда и только тогда, когда:

• 1)    все корни р _к полухарактеристического многочлена / ( ц ) вещественны и неположительны;

• 2)    все элементарные делители матрицы JA просты.

Для кубического многочлена / ₃ (ж) условие 1 проверяется с помощью следующего утверждения.

Утверждение 2 ([2, теорема 2.2]). У многочлена / _п (х) для п = 2,3 все корни вещественные и отрицательные тогда и только тогда, когда выполнены следующие неравенства:

ai > 0, г = 1,..., п, и D(/n) > 0, где D(/n) — дискриминант многочлена /п(х).

Условие 2 эффективно проверяется с помощью утверждения.

Утверждение 3. Пусть Л * — корень кратности к характеристического многочлена /( Л ) матрицы J А . Все соответствующие элементарные делители матрицы JA просты тогда и только тогда, когда rang(JA — Л* Е ) = т — к , где т = dim JA .

Как известно, устойчивость положения равновесия системы (19) может быть нарушена возмущениями порядка 3 и выше. Если квадратичная форма H ₂ ( z ) является знакоопределенной, то по теореме Лагранжа — Дирихле возмущения высоких порядков не влияют на устойчивость. Далее полагаем, что форма H ₂ ( z ) знакопеременная.

С практической точки зрения вполне достаточной является более слабая, чем устойчивость по Ляпунову, формальная устойчивость , предложенная Ю. Мозером в [19].

Определение 10. Положение равновесия z = 0 гамильтоновой системы является формально устойчивым , если существует возможно расходящийся степенной ряд, который является формальным положительно определенным первым интегралом.

Наличие формальной устойчивости гарантирует, что на конечном, но большом интервале времени возмущенная траектория остается близкой к невозмущенной.

В работе автора [1] предложена некоторая схема исследования формальной устойчивости положения равновесия, основанная на теореме Брюно (см. [9] или [14, гл. 5, § 2]). Для реализации этой схемы требуется разбить область П ₁ на подобласти W резонансными множествами ^ _{р :1} (/( ц )), P = 4,9,16. При этом следует ограничиться только той частью П ₁ , в точках которой полухарактеристический многочлен /( ц ) имеет только отрицательные вещественные корни. В силу утверждения 2 достаточно описать взаимное расположение дискриминантного множества Т>(/ ( ц )) и резонансных множеств ^ _{р :1} (/( ц )), р = 4, 9,16 в октанте о « > 0, г = 1, 2, 3.

Согласно формулам (17) и (18) каждая из резонансных поверхностей ^ _{р :1} (/( ц )) касается дискриминантной поверхности Р(/( ц )) вдоль кривых L _i , 2. Сечение указанных выше поверхностей плоскостью a _i = const > 0 показано на рисунке 2 для а ₁ = 2, р = 4.

Две резонансные поверхности Р _р 1 _:1 (/( ц )) и Р _р 2 _:1 (/( ц )), р1 , 2 G {4, 9,16}, пересекаются вдоль кривых C j . Параметризацию кривых C j нетрудно найти, используя следующие рассуждения. Пусть на поверхности Р _р 1 _:1 (/( ц )) многочлен /( ц ) имеет два порождающих корня t _i и t ₂ , а на поверхности Р _р 2 _:1 (/( ц )) — м ₁ и м ₂ . Тогда на этих поверхностях /( ц ) представляется в виде

/( ц ) = ( ц - t 1 )( ц — P 1 t 1 )( ц — t 2 ) = ( ц — М 1 )( ц — P 2 M 1 )( ц — М 2 ).

В точках пересечения поверхностей тройки корней должны совпадать. Нетрудно видеть, что имеются четыре различных набора значений параметров t _i , t ₂ ,M _i ,M ₂ , для которых две тройки ненулевых корней совпадают:

• 1)    t 2 = P 2 t i , M i = t i , М 2 = Р 1 t i ;

• 2)    t 2 = Р 1 Р 2 t i , М 1 = Piti , М 2 = t i ;

• 3)    t 2 = —, M i = —, М 2 = P i t i ; P 2         P i

Piti           Piti .

• ^{4)    t} 2 = ----, ^M i = ----, ^M 2 = ^t i .

P 2          P 2

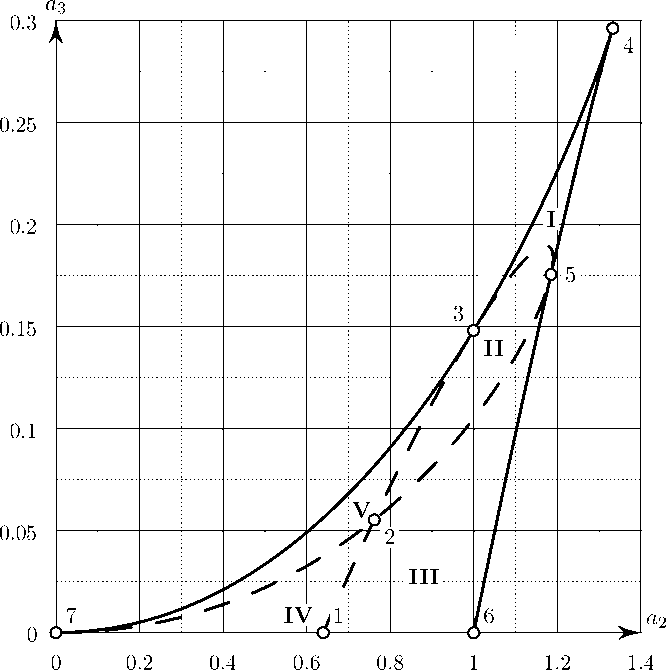
Рис. 2. Сечение дискриминантной 7? ( / ( ц )) (сплошная линия) и резонансной ^ 4:1 ( У ( ц )) (штриховая линия) поверхностей плоскостью а 1 = 2. Кружками показаны особые точки, граничные точки и точки касания

Подставляя указанные выше значения параметра £ 2 , получим параметризацию кривых C j , 3 = 1,2,3,4. Сечение резонансных поверхностей плоскостью а 1 = const > 0 показано на рисунке 3 для а1 = 2, р1^ = 4, 9,16.

В области П 1 вне резонансных поверхностей ^ _{р :1} (/( ц )), р = 4, 9,16, неподвижная точка z = 0 формально устойчива [9]. Для точек на этих резонансных поверхностях требуется дополнительное исследование формальной устойчивости, которое можно сделать, вычислив нормальную форму функции Гамильтона Н ( z ) [8; 11; 14] до 4-го порядка включительно.

Укажем несколько задач, где исследование формальной устойчивости может быть проведено с помощью описанного выше метода:

• •    устойчивость положения равновесия некоторой гироскопически стабилизированной системы [1; 2];

• •    устойчивость пространственных точек либрации в задаче Хилла с учетом солнечного ветра и несферичности потенциала Земли [18].

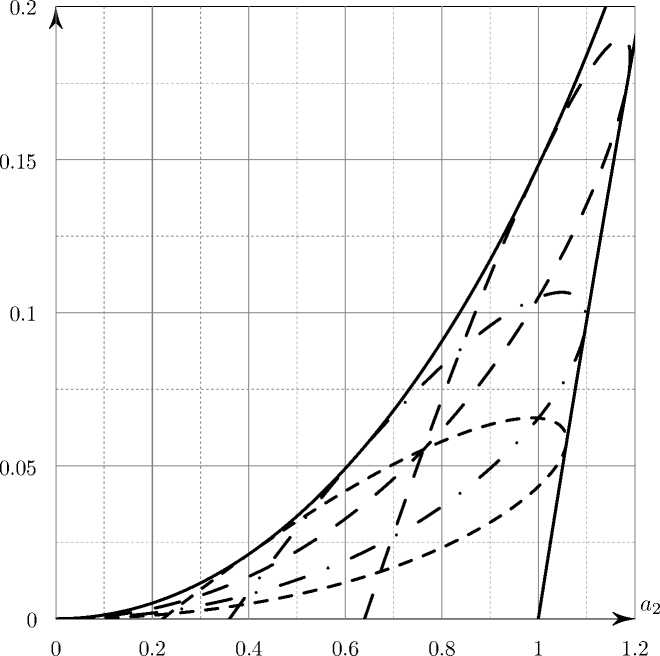
Рис. 3. Сечение резонансных поверхностей ^ _р:1 ( / ( ц )) плоскостью Q 1 = 2 для значений р = 4 (длинный штрих), р = 9 (штрих-пунктир), р =16 (короткий штрих). Сплошной линией показана граница области П 1

Заключение

Резонансное множество ^(/ _п ) многочлена / _п (ж) может рассматриваться как некоторое обобщение дискриминантного множества P(/ n ) для случая, когда отношение пары корней равно некоторому числу. Резонансное множество состоит из конечного набора алгебраических многообразий размерностей от 1 до п — 1, число которых определяется числом р(п) разбиений степени п многочлена / _п (ж). Каждое из этих многообразий выделяется соответствующим идеалом, состоящим из обобщенных субдискриминантов, и допускает полиномиальную параметризацию.