Резонансные особенности волноводных брэгговских структур сверхвысокочастотного диапазона

В настоящее время брэгговские структуры СВч-диапазона, называемые также фотонными кристаллами или периодическими структурами с фотонной запрещенной зоной, находят широкое применение при создании различных типов СВч-устройств, среди которых перестраиваемые резонаторы, направленные ответвители, миниатюрные антенны, согласованные нагрузки, различные типы СВч-фильтров, в том числе с управляемыми характеристиками [1–8].

Одним из направлений исследований в области периодических структур с фотонной запрещенной зоной, в основе которого лежит существование аналогии между поведением электромагнитной волны, распространяющейся в периодической структуре, и взаимодействием электронов с периодическим потенциалом кристаллической решетки реальных кристаллов, является теоретическое обоснование и экспериментальное подтверждение интерфейсных резонансных эффектов, связанных с изменением или нарушением периодичности брэгговских структур и имеющих аналоги из области физики твердого тела, также непосредственно связанных с модифика- цией кристаллической решетки. Одним из таких эффектов является возникновения в сверхвысокочастотных брэгговских гетероструктурах аналога уровней Тамма.

Поверхностные электронные состояния Тамма появляются на границе полубесконечного кристалла и характеризуются дискретным энергетическим спектром и волновыми функциями, экспоненциально затухающими по мере удаления от поверхности в глубину кристалла и в пространство вне его [9]. В [10] было предложено расширенное определение таммовских состояний, как состояний, являющихся внутренними состояниями границы гетероперехода при наличии переходного (интерфейсного) слоя.

На границе брэгговской структуры возможна локализация электрического поля при контакте брэгговской структуры с однородным слоем, характеризующимся отрицательной диэлектрической проницаемостью (проводящая среда на частотах ниже плазменной) или отрицательной магнитной проницаемостью (магнитная среда на частоте в окрестности ферромагнитного резонанса). Такая локализация электрического поля

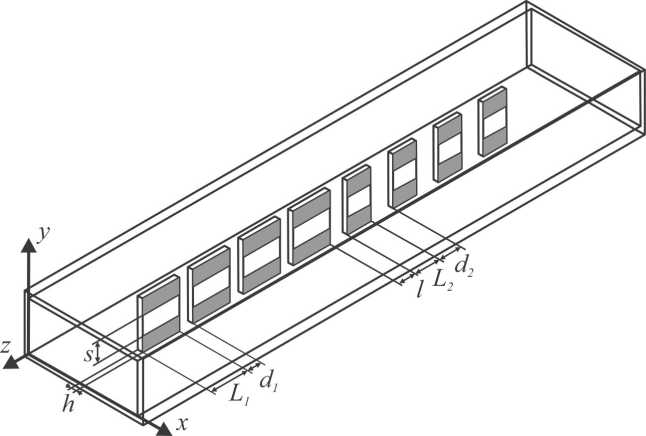
Рис. 1. Модель гетероструктуры, состоящей из двух брэгговских структур на основе волноводно-щелевых линий передачи, имеющих различные размеры элементарных ячеек трактуется как поверхностное таммовское состояние в брэгговской структуре. При этом на амплитудно-частотной характеристике брэгговской структуры, контактирующей с однородным слоем, наблюдается узкий пик коэффициента прохождения электромагнитной волны, связанный с возникновением таммовского состояния [11–13].

В брэгговской структуре аналог состояния Тамма также может встречаться на границе двух соединенных брэгговских структур с различными размерами элементарных ячеек при перекрытии запрещенных зон этих двух кристаллов [11; 14]. Такую систему из двух брэгговских структур с идеальной стыковкой можно считать идеальной брэгговской гетероструктурой по аналогии с идеальным гетеропереходом, который образуется между полупроводниками с абсолютно одинаковыми постоянными решетки. Изменение электрофизических параметров или полное отсутствие одного из слоев элементарной ячейки, находящейся в месте контакта брэгговских структур следует трактовать как нарушение идеальности брэгговской гетероструктуры, которое и выполняет роль интерфейса между двумя брэгговскими структурами и обеспечивает возникновение таммовского состояния на границе между ними, характеризующегося локализацией в области интерфейса пучности распределения электрического поля электромагнитной волны с максимальной напряженностью.

Важной особенностью брэгговских структур СВч-диапазона является тот факт, что в качестве периодически повторяющихся элементов могут быть использованы отрезки различных типов широко применяемых в СВч-технике линий передачи. Общий вид исследуемой брэгговской СВч-структуры на основе волновод- но-щелевых линий [15; 16], составленной из двух подсистем, имеющих различные размеры элементарных ячеек, представлен на рис. 1. В центре поперечного сечения прямоугольного волновода X-диапазона (22.86 мм х 10.16 мм) в E-плоскости размещались две группы периодически расположенных отрезков щелевой линии передачи, образующих в совокупности брэгговскую гетероструктуру. Щелевая линия первой подсистемы брэгговской гетероструктуры выполнена на поликоровой (А^Оз, £ = 9,6) пластине длиной L1 = 15 мм, шириной 10.16 мм и толщиной 1 мм. На одну сторону пластины было нанесено золотое покрытие толщиной 0.01 мм, ширина щели в покрытии составляла s = 4.0 мм. Отрезки первой подсистемы волноводно-щелевой линии передачи разделялись отрезками регулярного волновода длиной d1 = 10 мм. Длина отрезков волноводно-щелевой линии второй подсистемы брэгговской гетероструктуры составляла L2 = 13 мм, а длина отрезков регулярного волновода d2 = 15 мм. Каждая из подсистем структуры состояла из четырех отрезков щелевой линии. Длины отрезков волноводно-щелевой линии передачи и регулярных отрезков волновода каждой из двух брэгговских структур были выбраны таким образом, чтобы частоты, соответствующие серединам запрещенных зон одной и другой брэгговских структур, максимально совпадали. При этом вследствие различной ширины запрещенных зон этих структур наблюдалось лишь их частичное перекрытие в частотной области.

численный расчет коэффициентов отражения и прохождения выполнялся с использованием программного обеспечения для трехмерного моделирования электромагнитных полей методом конечных элементов ANSYS HFSS. частотные зависимости коэффициентов отражения и прохождения брэгговской гетероструктуры исследовались с помощью векторного анализатора цепей Agilent PNA-L Network Analyzer N5230A в диапазоне частот 8–12 ГГц.

Как следует из результатов эксперимента и расчета, при длине l регулярного отрезка волновода, соединяющего две брэгговские структуры и играющего роль интерфейсного слоя, равной длине регулярных отрезков первой или второй брэгговской структур, АчХ «идеальной» брэгговской гетероструктуры характеризуется наличием запрещенной зоны с коэффициентом пропускания, достигающим –45 дБ (см. кри-

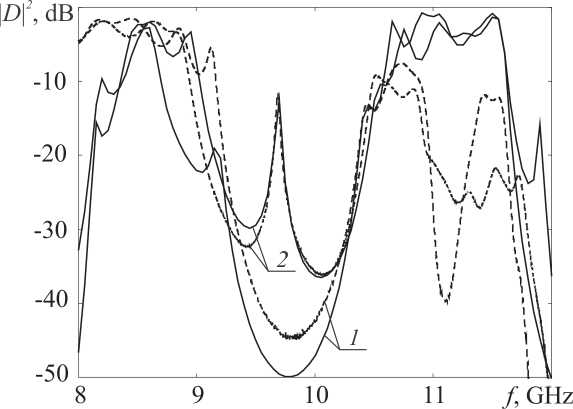
Рис. 2. Экспериментальные (штриховые кривые) и расчетные (сплошные кривые) частотные зависимости коэффициентов прохождения | D |² для брэгговской гетероструктуры, при различной длине интерфейсного слоя l , mm: 1 – 10 мм, 2 – 1 мм

вые 1 на рис. 2). При этом в запрещенной зоне не наблюдался пик коэффициента прохождения электромагнитной волны, связанный с возникновением локализованного состояния. При длине интерфейсного слоя l , равной 1 мм, пик прохождения электромагнитной волны возникал в середине запрещенной зоны (кривые 2 на рис. 2) фотонной гетероструктуры.

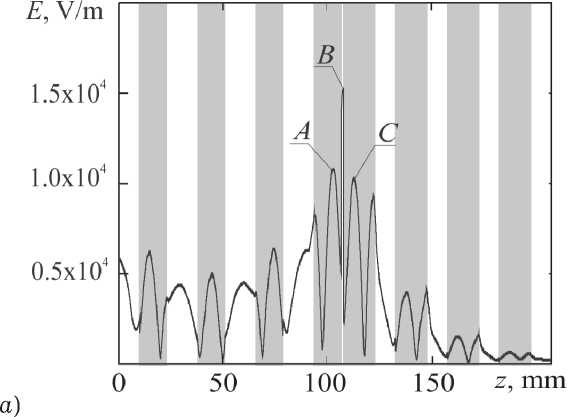
Результаты расчета напряженности электрического поля электромагнитной волны на частоте f _Tamm, соответствующей пику коэффициента прохождения электромагнитной волны в запрещенной зоне, демонстрируют локализованную на интерфейсной границе двух последовательно соединенных брэгговских структур пучность распределения электрического поля электромагнитной волны с максимальной напряженностью (рис. 3). Анализ распределения поля в плоскостях поперечного сечения волновода, проходящих через пучности стоячей волны на отрезках волноводно-щелевой линии первой и второй брэгговских структур и через пучность на интерфейсной границе, свидетельствует о существенной локализации поля в середине широкой стенки волновода.

Таким образом, установлено, что локализованные состояния на границе двух брэгговских структур возникают лишь при наличии на этой границе интерфейсного элемента с характеристиками, отличными от характеристик как одной, так и другой брэгговской структуры. В «идеальной» брэгговской гетероструктуре там-мовские поверхностные состояния не возникают.

Амплитудно-частотные характеристики брэгговских структур СВч-диапазона демонстрируют наличие чередующихся разрешенных и

б )

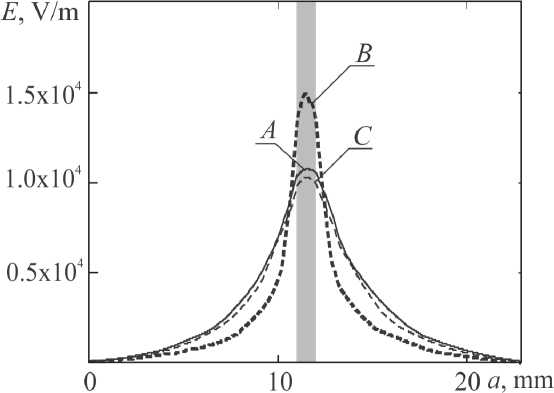
Рис. 3. Распределение напряженности электрического поля электромагнитной волны внутри брэгговской гетероструктуры на частоте пика коэффициента прохождения в запрещенной зоне: а ) вдоль направления распространения волны; б ) в плоскостях поперечного сечения волновода ( A , B , C ) на рисунке a f _Tamm = 9.686 ГГц. Темным цветом на рисунке a отмечены области, которые заняты отрезками волноводнощелевой линии передачи, светлым обозначены области, занятые регулярными отрезками волновода

запрещенных диапазонов частот для распространения электромагнитного излучения. Данная особенность применяется для создания различных типов СВч-устройств, в частности, СВч-фильтров, являющихся одними их самых распространенных компонентов современных радиоэлектронных систем [1–8]. Наряду с полосовыми фильтрами [6; 17–22], предназначенными для распространения сигналов на выбранных частотах, фильтры заграждения необходимы для подавления нежелательных сигналов. Современные СВч-фильтры заграждения, выполняемые как с использованием различных типов планарных линий передачи, так и в волноводном исполнении [23–30], наряду с высоким коэффициентом ослабления в выбранной полосе частот, должны характеризоваться коэффициентом прохождения электромагнитного излучения близким к единице вне полосы заграждения.

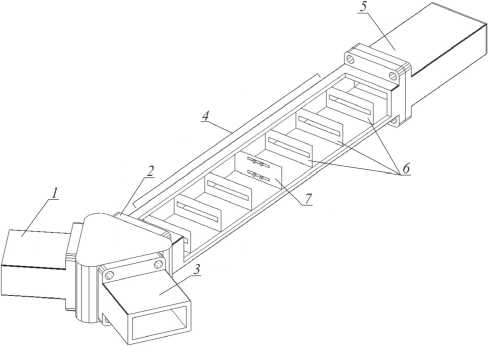
Рис. 4. Брэгговская структура на резонансных диафрагмах в схеме на отражение с Y -циркулятором. 1 – вход Y -циркулятора; 2 , 3 – выходы Y -циркулятора; 4 – брэгговская структура; 5 – согласованная нагрузка; 6 –диафрагмы; 7 – центральная диафрагма с n–i–p–i–n -диодными структурами

Наличие явно выраженных запрещенных зон на характеристиках брэгговских структур СВч-диапазона позволяет использовать их в качестве полосовых фильтров заграждения, однако вне полосы заграждения, то есть в области разрешенных зон, коэффициент прохождения имеет «изрезанную», то есть частотно зависимую характеристику. Использование Y -циркулятора, в одно из плеч которого включена брэгговская структура, позволяет уменьшить «изрезанность» частотной характеристика коэффициента прохождения СВч-волны в разрешенной зоне брэгговской структуры (рис. 4). При подаче входного СВч-сигнала на вход 1 идеального Y -циркулятора сигнал на выход 3 Y -циркулятора поступает только при наличии отраженной волны на его выходе 2 , следовательно, при подключении брэгговской структуры с согласованной нагрузкой на выходе 2 Y -циркулятора, коэффициент прохождения D сигнала с входа 1 Y -циркулятора на выход 2 Y -циркулятора определяется коэффициентом отражения брэгговской структуры R . В области частот, определяющих запрещенную зону брэгговской структуры, коэффициент прохождения D сигнала с входа 1 Y -циркулятора на выход 3 Y -циркулятора близок к единице, что обеспечивает формирование частотнонезависимой характеристики разрешенной зоны.

Для создания устройств с электрически управляемым коэффициентом прохождения была использована брэгговская структура, состоящая из семи периодически расположенных в прямоугольном волноводе трехсантиметрового диапа-

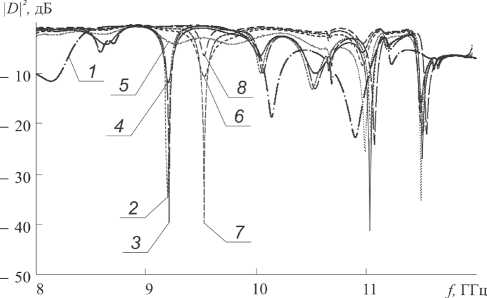
Рис. 5. Экспериментальные частотные зависимости D ² сигнала из плеча 1 в плечо 3 Y -циркулятора с брэгговской структурой в схеме на отражение. 1 – без нарушений; 2 – 8 – с n–i–p–i–n --матрицей в качестве нарушения периодичности при различных значениях тока I, мА: 2 – 0.0; 3 – 0.0005; 4 – 0.092; 5 – 0.660; 6 – 3.36; 7 – 8.15; 8 – 193.5

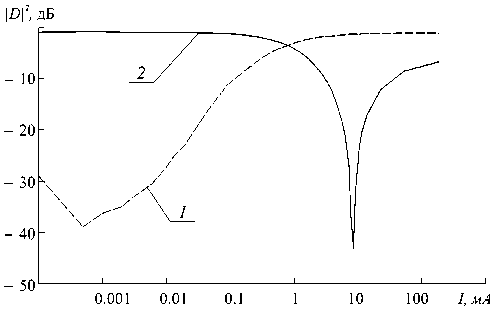
Рис. 6. Зависимости коэффициента прохождения от величины протекающего через n–i–p–i–n -структуру тока на частотах примесных мод колебаний ^_эксп = 9.22 ГГц (кривая 1 ) и f _{2 э} к _сп = 9.56 ГГц (кривая 2 )

зона металлических резонансных диафрагм на расстоянии L = 20 мм друг от друга. Ширина и высота щелей диафрагм выбирались равными 20 мм и 2 мм, В центральной диафрагме располагалась n–i–p–i–n -диодная матрица, состоящая из четырех диодных элементов, расположенных в двух прямоугольных щелях, размеры каждой из которых составляли 10.5 х 1.0 мм².

Измерение передаточной характеристики D исследуемой брэгговской структуры проводились в схеме с Y -циркулятором с помощью векторного анализатора цепей Agilent Microwave Network Analyzer N5242A PNA-X в диапазоне частот 8–12 ГГц.

Как следует из результатов эксперимента, частотная зависимость коэффициента прохождения сигнала из плеча 1 в плечо 3 Y -циркулятора с брэгговской структуры в схеме на отражение характеризуется наличием плоской разрешенной зоны в диапазоне частот 8.5–9.85 ГГц (кривая 1 на рис. 5). Введение в брэгговскую струк-

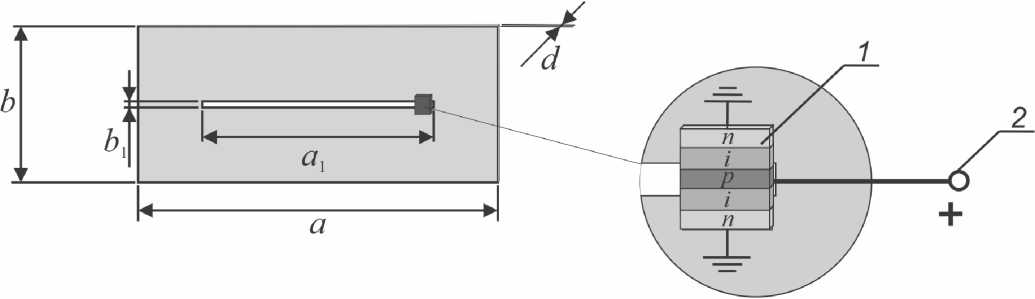
Рис. 7. Конструкция центральной диафрагмы брэгговской структуры с электрически управляемым размером щели. 1 – n–i–p– i–n -диодная структура; 2 – источник постоянного напряжения. A = 23 мм, b = 10 мм, d = 10 мкм, a ₁ = 15.3 мм, b ₁ = 0.33 мм

туру n–i–p–i–n -матрицы в качестве нарушения приводит к появлению примесной моды затухания колебаний в разрешенной зоне на частоте f = 9.22 ГГц. Изменение величины управляющего тока n–i–p–i–n -структуры от 0 до 0.5 мкА приводит к уменьшению коэффициента прохождения на частоте примесной моды затухания колебаний f _{1 эксп} от –29.7 дБ до –39.7 дБ. Дальнейшее увеличение управляющего тока от 0.5 мкА до 193.5 мА приводит к монотонному увеличению коэффициента прохождения на частоте f _{1 эксп} от –39.7 дБ до –0.8 дБ.

Такое поведение передаточной характеристики на частоте примесной моды связано с тем, что при малых токах инжекции 0–0.5 мкА n–i–p–i– n -структура поглощает электромагнитное излучение, что приводит существенному уменьшению его отражения от брэгговской структуры, и сигнал на выход 3 Y- циркулятора практически не поступает. При увеличении тока инжекции до 193.5 мА n–i–p–i–n -структура практически полностью отражает электромагнитное излучение, что приводит к передаче сигнала на выход 3 Y -циркулятора с минимальным ослаблением. Увеличение тока, протекающего через n–i– p–i–n -структуру, до значений больших 0.66 мА приводит к возникновению примесной моды затухания колебаний на частоте f _{2 эксп} = 9.56 ГГц, отличной от f _{1 эксп} . При этом на частоте f _{2 эксп} с увеличением протекающего через n–i–p–i–n -структуру тока в диапазоне от 0.0 мА до 8.15 мА D уменьшается от –0.82 дБ до –43.27 дБ. Дальнейшее увеличение управляющего тока приводит к монотонному росту D на частоте f _{2 эксп} (кривая 8 на рис. 5).

На рис. 6 представлены зависимости коэффициента прохождения D сигнала из плеча 1 в плечо 3 Y -циркулятора с брэгговской структурой в схеме на отражение на частотах примесных мод затухания колебаний брэгговской структуры f _{1 эксп} . и f _{2 эксп} от величины протекающего через n–i–p–i–n -структуру тока.

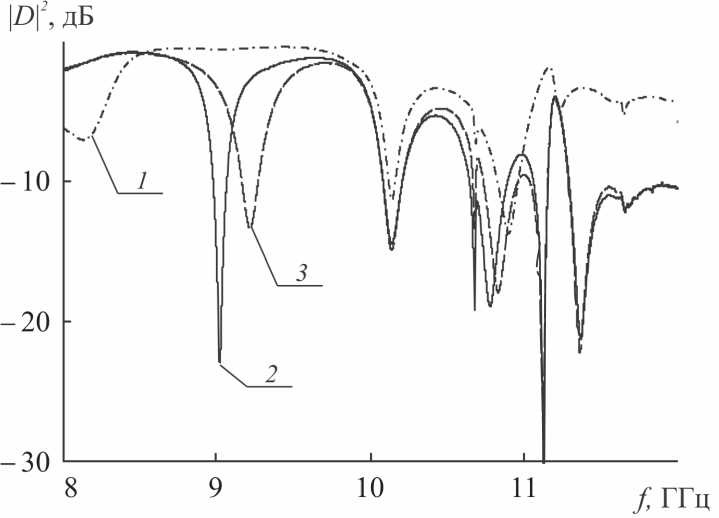
Рис. 8. Экспериментальные частотные зависимости D ² сигнала из плеча 1 в плечо 3 циркулятора с брэгговской структурой 1 – без нарушения и с электрически управляемым размером щели диафрагмы при наличии и отсутствии протекающего через n–i–p–i–n- структуру прямого тока I , мА: 2 – 0.0, 3 – 550 мА

Таким образом, предложенная схема электрически управляемого фильтра заграждения, выполняющего роль модулятора и переключателя СВч-сигнала, на основе брэгговской структуры на резонансных диафрагмах, реализованная с использованием Y -циркулятора, позволяет обеспечить на частотах примесных мод затухания в прямом режиме потери запирания –43.27 дБ и прямые потери на прохождение равные –0.82 дБ. В инверсном режиме прямые потери составляют –0.82 дБ и потери запирания –39.7 дБ.

Для реализации в схеме с Y -циркулятором электрически управляемого фильтра заграждения с использованием брэгговской структуры на резонансных диафрагмах с электрически управляемым размером щели диафрагмы, выполняющей роль нарушения, может быть использована конструкция, в которой вблизи одного из краев центральной диафрагмы со щелью уменьшенной ширины расположена n–i–p–i–n -структура (рис. 7) [31].

При больших прямых токах n–i–p–i–n-диодная структура выполняет роль проводящего включения, уменьшающего ширину щели диафрагмы и смещающего положение примесной моды затухания колебаний в сторону высокочастотного края запрещенной зоны.

На рис. 8 представлены АчХ коэффициентов прохождения D сигнала из плеча 1 в плечо 3 Y -циркулятора с брэгговской структурой с электрически управляемым размером щели диафрагмы, выполняющей роль нарушения.

Как следует из результатов эксперимента, в схеме с Y -циркулятором при включении в брэгговскую структуру на резонансных диафрагмах центральной диафрагмы с электрически управляемым размером, выполняющей роль нарушения, в разрешенной зоне передаточной характеристики СВч брэгговской структуры возникает примесная мода затухания колебаний на частоте f _{1 эксп} = 9.03 ГГц, которая смещается по частоте на величину, равную 160 МГц, в сторону высокочастотного края запрещенной зоны при пропускании через n–i–p–i–n -диодную структуру прямого тока, равного 550 мА. При этом на частоте примесной моды колебаний 9.03 ГГц наблюдается увеличение коэффициента прохождения от –20.35 дБ при I = 0 мА до –1.65 дБ при I = 550 мА.

Следует отметить, что компьютерное моделирование передаточной характеристики СВч фотонного кристалла с электрически управляемым размером щели центральной диафрагмы показывает возможность значительного уменьшения прямых потерь при достижении удельной электропроводности i -слоя n–i–p–i–n -структуры величины, равной 10⁵ См/м. Такое увеличение удельной электропроводности i -слоя может быть достигнуто при использовании n–i–p–i–n -структур с гетеропереходами, обеспечивающими более высокий уровень инжекции по сравнению с традиционными гомопереходами.

Таким образом, экспериментально исследовано возникновение резонансных особенностей, соответствующих таммовским поверхностным состояниям в брэгговской структуре СВч-диапазона, составленной из двух последовательно соединенных брэгговских структур, имеющих разные размеры элементарных ячеек и выполненных в виде волноводно-щелевых линий передачи.

Показана возможность использования отражательных свойств брэгговской структуры с резонансными диафрагмами в схеме с Y-циркулятором для создания фильтров заграждения с управляемыми n–i–p–i–n-диодами частотными характеристиками, обладающих уровнем запирания в полосе заграждения более 43 дБ и потерями вне полосы менее 0.8 дБ.

Работа выполнена при финансовой поддержке Министерства образования и науки РФ (государственное задание № 8.7628.2017/БЧ) и стипендии Президента РФ (СП-3301.2018.3).