Результаты экспериментов по смешиванию сыпучих материалов в вибрационном смесителе

Вибрационные смесители сыпучих материалов по сравнению с механическим смешиванием имеют ряд преимуществ: пониженный расход электроэнергии, высокая технологическая эффективность (надежность), высокая производительность, сохранение целостности частиц смешиваемых ингредиентов.

Смешивание сыпучих материалов происходит практически в любом вибрационном смесителе, но для получения качественного смешивания необходимо создание смесителей более совершенных конструкций с целенаправленной вибрацией.

Недостаточно изучена энергия, затрачиваемая на вибрационное смешивание сыпучих материалов, и зависимость ее от параметров вибрации. Имеет смысл экспериментально изучить расход энергии, передаваемой от рабочих поверхностей смесителя к смешиваемым ингредиентам, для получения необходимой однородности готовой смеси.

Результаты экспериментального исследования. Процесс смешивания исследовали в вибрационном смесителе, состоящем из торообразной камеры, жестко закрепленной на платформе, которая соединена с рамой тремя плоскими пружинами. Торообразная камера снабжена штуцером для ввода смешиваемых ингредиентов и вывода готового продукта. Платформа с камерой приводилась в колебательное движение электродвигателем посредством кривошипно-шатунного механизма.

Отличительная особенность рассматриваемого смесителя – простота конструкции смесительной камеры, возможность ее смены на камеру другой вместимости или формы, а также создание пространственных винтовых колебаний камеры.

Процесс вибрационного смешивания побуждался ударными воздействиями плоскости дна смесителя на сыпучий материал. Более интенсивно процесс смешивания проходил в режиме непрерывного полета, условие которого определены уравнением [1]:

A ω ^{2 g}

cos ω t ₀ sin β ≥ π ,

где A – амплитуда колебаний; ω – частота колебаний; t 0 – момент времени отрыва слоя от плоскости дна; β – угол направления колебаний.

Для определения энергии, необходимой для смешивания, воспользуемся второй теоремой Карно для не вполне упругого удара [2]:

_{E =} 1 - e    m ν w ν ² _,

1 + e ν 2

где e – коэффициент восстановления, который показывает, на сколько восстанавливается нормальная составляющая скорости материальной точки после удара; mν – масса; wν – началь- ная скорость.

Скорость частиц определяем из следующих соображений. В момент начала полета (отрыва от плоскости дна) слой сыпучего материала имеет скорость, равную скорости дна, определяемую уравнением колебательного движения плоскости дна [1]:

w = - Л ю sin to 1 0 .

Сделано допущение, что при падении слоя на поверхность дна, скорость его равна скорости начала полета.

Потерю энергии при ударе слоя о поверхность дна смесителя за один цикл (отрыв слоя – полет слоя – падение слоя на плоскость) представим в виде:

E =

1 - e ) m _v ( - F ro sin ю 1 ₀ ) 2

1 + e J        2        .

Коэффициент восстановления e определяли экспериментально. С высоты h =0,2 м поштучно подавали очищенное пшено, которое падало на стекло. Принято допущение, что стекло – абсолютно твердая поверхность и поэтому его упругие свойства не будут влиять на измерение коэффициента восстановления растительного материала – пшена. Процесс падения и отскока зерен пшена снимали видеокамерой. Затем расшифровывали видеокадры, по которым определяли высоту отскока. На рис.1 показан видеокадр процесса определения высоты отскока.

Рис.1. Видеокадр процесса определения коэффициента восстановления: светлые черточки – зерна, движущиеся вниз; белые точки – максимальная высота отскока, при которой скорость зерна равна нулю

Коэффициент восстановления определяли по формуле:

e = V omp/ V пад ,                                               (*)

где Vотр = ^2ghотр - скорость конца удара; Vпад = 72gh - скорость начала удара; hотр - высота от- скока.

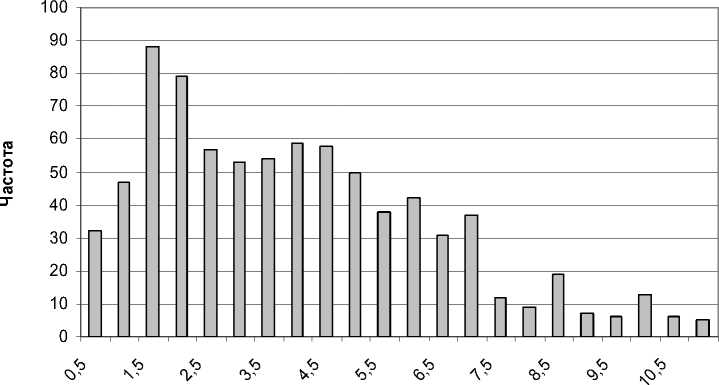
На рис.2 показана гистограмма распределения высоты отскока зерен пшена при падении с высоты h =0,2 м на абсолютно твердую поверхность.

Характеристики распределения высоты отскока следующие: среднее значение высоты отскока h cp =0,0399 м, среднеквадратичное отклонение σ =0,0243 м.

Высота отскока, см

Рис.2. Гистограмма распределения высоты отскока

Для проверки гипотезы нормального распределения по критерию Колмогорова – Смирнова составлена таблица.

Проверка принадлежности нормальному распределению вариации коэффициента восстановления e по Колмогорову – Смирнову

Класс, м	LO О о о	о о	LO о о	rsl О о	LO Г\1 О о	СП о о	СП о о	о о	LO о о	LO о о	LO О о	о о	LO о о	6 о	LO о о	00 о о	LO 00 о о	<т> о о	LO <т> о о	о о	LO о о	о
Эмпирическое распределение	32	47	88	79	57	53	54	59	58	50	38	42	31	37	12	9	19	7	6	13	6	5
Теоретическое распределение	27	25	23	20	16	13	10	7	5	3	2	1	1	0	0	0	0	0	0	0	0	0
d	5	22	65	59	41	40	44	52	53	47	36	41	30	37	12	9	19	7	6	13	6	5

Проверка гипотезы нормального распределения по критерию Колмогорова – Смирнова показала, что

X = d max- = -52= = 2,29 >  1,95 , n 802

где n – количество наблюдений; d _max – максимальная разность между частотой эмпирического и теоретического распределения по классам.

Полученное значение λ превышает порог доверительной вероятности α =0,99, и поэтому нулевая гипотеза отвергается, иначе – эмпирическое распределение высоты отскока нельзя отнести к нормальному закону распределения. Это может быть объяснено тем, что очищенные зерна пшена имеют форму не идеальной сферы, а эллипсоида, и высота отскока определена при допущении, что вектор скорости отражения был вертикальный, что действительно не для всех вариантов.

Используем функцию MS Excel НОРМСТОБР(z) для вычисления доверительного интервала для высоты отскока по следующему выражению:

h _отр ±-^ НОРМСТОБР(0,95) ,

n где z=0,95 – двухсторонняя доверительная вероятность.

Согласно расчетам 95%-й доверительный интервал для h отр находится в диапазоне h отр = 0,0399 ± 0,0015 м.

В результате расчета по формуле (*) получено значение коэффициента восстановления e =

, 0,0399 = 0,447 .

0,2

С учетом доверительного интервала для высоты отскока определен коэффициент восстановления: e = 0,447 ± 0,08 .

Количество циклов смешивания за 1 с при угловой частоте колебаний ω :

to

.

c =---

2 n

Мощность на смешивание массы сыпучего продукта в смесителе непрерывного действия производительностью q имеет вид:

sin to t оср )²

• ¹    - e to q ^{( A to (} 1 + e ) 2 n

  .

  
  

Максимальное значение мощности на вибрационное смешивание сыпучих материалов получено при значении sin( to 1 0 ) = 1 . Поэтому для оценки необходимой мощности можно применить упрощенную формулу:

N = (т- e!A 2 to ! q , \ 1 + e / 4п

ППоб где to =   °б - круговая частота колебаний; nоб - частота вращения побудителя колебаний.

Заключение. В результате исследования получена зависимость, связывающая мощность на смешивание с параметрами вибрации. Полная мощность на привод может быть получена с учетом затрат энергии на холостой ход и на перемещение материала внутри смесителя в зависимости от его конструкции.