Результаты оценки интенсивности пыления хвостохранилищ

Данная работа является естественным продолжением исследований специалистов КНЦ РАН по проблеме пыления хвостохранилища АНОФ-2 (г. Апатиты, Мурманская обл.) на базе методов численного моделирования [1–5]. На предыдущем этапе авторами выполнен анализ существующих подходов по оценке интенсивности пыления (пустыни, хвостохранилища и др.). Некоторые результаты выполненного исследования представлены в докладах на российских и международных конференциях [6–8]. В наиболее полной форме обобщающий итог анализа направлен авторами в авторитетное горное издание "Физико-технические проблемы разработки полезных ископаемых" (ФТПРПИ).

Коротко напомним основные результаты исследования. Рассмотрен круг подходов по оценке интенсивности пыления (зависимости Семенова О. Е. [9] и Westphal D. L. et al. [10], схемы DEAD [11], GOCART [12], обобщение по работам советских ученых [1–3]), наиболее приемлемых и общепризнанных для решения практических задач по исследованию влияния скорости ветрового потока и высоты пылящей поверхности на загрязнение атмосферы для района г. Апатиты от воздействия близлежащего хвостохранилища АНОФ-2.

Авторами выполнен сравнительный анализ расчетных кривых вертикального потока массы на примере двухмерной аэродинамической модели района "хвостохранилище АНОФ-2 – г. Апатиты" при вариации скорости ветрового потока в диапазоне от 5 м/с до 23 м/с. Высота пылящей поверхности относительно основания модели составляет 74 м, что отвечает максимальной проектной высоте объекта (200 м). По результатам анализа сделан предварительный вывод, что наиболее приемлемыми для последующих исследований загрязнения приземного слоя атмосферы вниз по ветровому потоку могут быть признаны зависимость Westphal D. L. et al. [10] и схема DEAD [11]. Именно эти зависимости дают минимальное расхождение результатов на всем рассмотренном диапазоне скорости ветрового потока. Отметим, что оба подхода базируются на функциональной зависимости потока массы от динамической скорости на высоте пыления в 4-й и 3-й степенях соответственно.

Схема DEAD (Dust Entrainment And Deposition) [11] описывает мобилизацию пыли через скорость трения (ветровое напряжение на границе раздела) на высоте пылящей поверхности, которая является функцией скорости ветра, размера шероховатости и устойчивости атмосферы. Поток массы сальтирующих частиц (горизонтальный поток массы) зависит от превышения ветровой скорости трения над пороговой скоростью трения ветра (критическая скорость начала переноса). Горизонтальный поток массы G может быть вычислен по формуле

G p = c P a u * p g

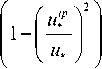
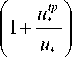
где c – константа; ρ _a – плотность воздуха; u _* – скорость трения ветра (динамическая скорость); g –ускорение свободного падения. В работе [11] значение константы c рекомендовано выбрать равной 2,61. Указывается, что это значение получено по результатам ветровых туннельных экспериментов. В выражении (1) динамическая скорость имеет размерность м/с.

Значение динамической скорости предлагается вычислять с помощью известного соотношения

К U = M₁₀-----------,

10 ln( H101Z0)’ где нижний индекс 10 отнесем к высоте +10 м (H10) над поверхностью пыления, т. е. u10; z0 – параметр шероховатости, м; κ – постоянная Кармана.

Напомним, что согласно терминологии в вопросах измерения процессов пыления различают горизонтальный ( G ) и вертикальный ( F ) потоки массы (ГПМ и ВПМ). Они имеют разные размерности: горизонтальный – [кг/(м ^. с)] и вертикальный – [кг/(м ^2. с)]. Для решаемой задачи интересен именно вертикальный поток массы, который в уравнениях конвективно-диффузионного переноса примеси на границе моделируемой области называют интенсивностью пыления. Обычно ВПМ и ГПМ связывают линейным соотношением F = α · G ¹ , где коэффициент пропорциональности имеет размерность [см ^–1 ], а его значение зависит от содержания глины в пылящей почве (при нулевом содержании глины α = 10 ^–6 [см ^–1 ]). В диссертационной работе ² коэффициент α определяют как массовую эффективность обдуваемости потоком. Обсуждаемый коэффициент является мерой того, насколько эффективно сальтирующие частицы способны бомбардировать поверхность с высвобождением большого количества мелкодисперсного материала.

Авторами статьи [10] предложена модель для исследования мобилизации и переноса пыли в пустыне Сахара. Указанная модель при условии выполнения двух критериев эмиссии (влажность не более 0,3, динамическая скорость не менее 0,6 м/с) для частиц песка размером от 0,2 до 160 мкм предлагает для вычисления ВПМ (это следует из приведенной размерности) использовать выражение

F = 2,9 - 10 - 14 u * [г/(см ²- с)].

В выражении (3) используется динамическая скорость с размерностью см/с.

Следуя авторам работ ³ , представляется возможным при рассмотрении турбулентного переноса пыли с хвостохранилища АНОФ-2 ограничиться частицами, размер которых не превышает 70 мкм.

Авторский подход и обсуждение результатов расчетов

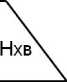
Для практической реализации оценок использована следующая последовательность действий. На рис. 1 представлена схема модели, которая принимается для обоснования величины скорости, необходимой для оценки вертикального потока массы частиц (интенсивности пыления): динамическая скорость на высоте пылящей поверхности u* определяется через осредненную горизонтальную компоненту скорости ветра на высоте +10 м над пылящей поверхностью u10.

Высота Нхв+10м

Поверхность хвостов

Основание модели

Поток воздуха

Референтная t высота 10 м /

Рис. 1. Схема модели под обоснование методики определения интенсивности пыления

Таким образом, для определения интенсивности пыления используем функциональные зависимости (1) и (3). На входной границе модели рассмотрим диапазон значений референтной скорости ветра u ref на высоте 10 м над основанием модели (от 5 до 23 м/с, например, с шагом 3 м/с). Задавая логарифмический профиль скорости на входной границе области (шероховатость принимается на уровне 0,05 м), выполняем расчет аэродинамики на базе стационарной стандартной ( k – ε)-модели [3–5]. Далее выполняем обработку расчетных аэродинамических параметров вдоль пунктирной линии (+10 м над поверхностью пыления): операцию осреднения горизонтальной компоненты скорости (рис. 2), т. е. получаем необходимые скорости ветра на высоте +10 м над пылящей поверхностью u ₁₀ .

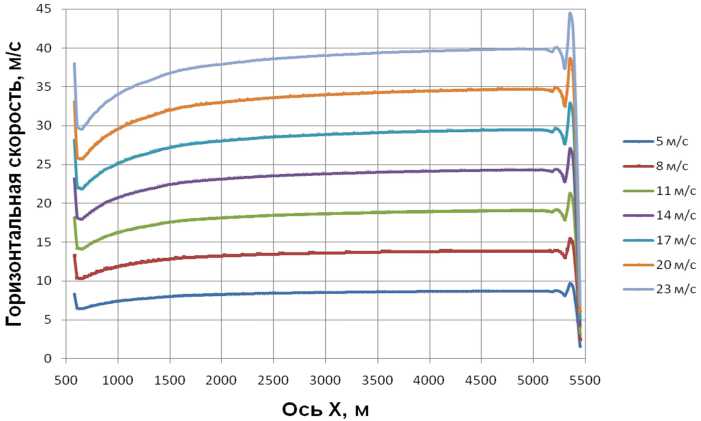
Рис. 2. Расчетные распределения горизонтальной скорости на высоте +10 м над поверхностью хвостохранилища u 10

Результаты обработки численных экспериментов для горизонтальной скорости на высоте +10 м над пылящей поверхностью, а также переход к динамической скорости u _* по формуле (2) обобщены в табл. 1.

Таблица 1

Осредненные значения горизонтальной скорости на высоте +10 м u 10 , соответствующие им значения динамической скорости u _*

Скорость ветра, м/с	u *	u 10
5	0,623	8,246
8	0,996	13,19
11	1,370	18,14
14	1,743	23,09
17	2,117	28,04
20	2,490	32,98
23	2,863	37,93

Гранулометрический состав (в графической форме) отвальных хвостов с поверхности устоявшегося пляжа хвостохранилища АНОФ-2 приведен в диссертационной работе А. В. Стриженок. "Управление экологической безопасностью намывных техногенных массивов ОАО "Апатит" в процессе их формирования" [13, с. 97, рис. 2.8]. Анализ гранулометрического состава отобранных проб пульпы и отвальных хвостов АНОФ-2 проводился на лазерном анализаторе распределения размеров частиц Horiba LA-950. Обработка графической информации позволила авторам получить количественные показатели по долям ("вес" интервала) каждого моделируемого класса размера частиц пыли (см. табл. 2), что необходимо для выполнения численных экспериментов по турбулентному переносу мультидисперсной примеси. Отметим, что "весовое" распределение интервалов, рассчитанное по данным работы [13], заметно отличается от того распределения, которое авторы использовали в своих прежних работах [1–3] и которое соответствует экспериментальным данным 70–80-х гг. прошлого столетия. В табл. 2 также приведены значения пороговой скорости u*tp для пыли класса крупности p до 70 мкм в диаметре с шагом 10 мкм, вычисленные по методике авторов работы [11], а также скорости оседания пыли, вычисленные в Стоксовом приближении [1–3] и необходимые для последующих вычислений конвективно-диффузионного переноса.

Значения "веса" интервала, пороговой скорости и скорости оседания в зависимости от срединного диаметра частиц пыли

Таблица 2

Срединный диаметр, мкм	"Вес" интервала, –	Пороговая скорость, м/с	Скорость оседания, м/с
5	0,022	0,951	0,00195
15	0,083	0,420	0,0175
25	0,142	0,295	0,0487
35	0,194	0,243	0,0955
45	0,209	0,218	0,1580
55	0,189	0,206	0,2360
65	0,161	0,201	0,3290

Результаты вычислений по формулам (1) (схема DEAD) и (3) (зависимость Westphal D. L. et al.) поинтервальных вертикальных потоков массы при вариации скорости ветрового потока с использованием необходимых параметров, приведенных в табл. 1 и 2, представлены в табл. 3 и 4 соответственно.

Таблица 3

Поинтервальные интенсивности пыления, вычисленные по схеме DEAD, при вариации скорости ветрового потока, кг/(м ²⋅ с)

Скорость ветра, м/с	Срединный диаметр, мкм
	5	15	25	35	45	55	65
5	***	0,628 ⋅ 10 –6	0,135 ⋅ 10 –5	0,190 ⋅ 10 –5	0,205 ⋅ 10 –5	0,186 ⋅ 10 –5	0,158 ⋅ 10 –5
8	0,130 ⋅ 10 –6	0,329 ⋅ 10 –5	0,570 ⋅ 10 –5	0,771 ⋅ 10 –5	0,823 ⋅ 10 –5	0,741 ⋅ 10 –5	0,630 ⋅ 10 –5
11	0,170 ⋅ 10 –5	0,867 ⋅ 10 –5	0,145 ⋅ 10 –5	0,195 ⋅ 10 –4	0,208 ⋅ 10 –4	0,188 ⋅ 10 –4	0,159 ⋅ 10 –4
14	0,435 ⋅ 10 –5	0,177 ⋅ 10 –4	0,293 ⋅ 10 –5	0,394 ⋅ 10 –4	0,421 ⋅ 10 –4	0,379 ⋅ 10 –4	0,322 ⋅ 10 –4
17	0,829 ⋅ 10 –5	0,311 ⋅ 10 –4	0,517 ⋅ 10 –5	0,695 ⋅ 10 –4	0,743 ⋅ 10 –4	0,669 ⋅ 10 –4	0,569 ⋅ 10 –4
20	0,138 ⋅ 10 –4	0,500 ⋅ 10 –4	0,831 ⋅ 10 –4	0,112 ⋅ 10 –3	0,120 ⋅ 10 –3	0,108 ⋅ 10 –3	0,917 ⋅ 10 –4
23	0,210 ⋅ 10 –4	0,751 ⋅ 10 –4	0,125 ⋅ 10 –3	0,169 ⋅ 10 –3	0,180 ⋅ 10 –3	0,163 ⋅ 10 –3	0,138 ⋅ 10 –3

Таблица 4

Поинтервальные интенсивности пыления, вычисленные по зависимости Westphal D. L. et al., при вариации скорости ветрового потока, кг/(м ²⋅ с)

Скорость ветра, м/с	Срединный диаметр, мкм
	5	15	25	35	45	55	65
5	0,958 ⋅ 10 –7	0,362 ⋅ 10 –6	0,619 ⋅ 10 –6	0,845 ⋅ 10 –6	0,910 ⋅ 10 –6	0,823 ⋅ 10 –6	0,701 ⋅ 10 –6
8	0,628 ⋅ 10 –6	0,237 ⋅ 10 –5	0,405 ⋅ 10 –5	0,554 ⋅ 10 –5	0,597 ⋅ 10 –5	0,540 ⋅ 10 –5	0,460 ⋅ 10 –5
11	0,225 ⋅ 10 –5	0,847 ⋅ 10 –5	0,145 ⋅ 10 –4	0,198 ⋅ 10 –4	0,213 ⋅ 10 –4	0,193 ⋅ 10 –4	0,164 ⋅ 10 –4
14	0,589 ⋅ 10 –5	0,222 ⋅ 10 –4	0,380 ⋅ 10 –4	0,519 ⋅ 10 –4	0,560 ⋅ 10 –4	0,506 ⋅ 10 –4	0,431 ⋅ 10 –4
17	0,128 ⋅ 10 –4	0,483 ⋅ 10 –4	0,826 ⋅ 10 –4	0,113 ⋅ 10 –3	0,122 ⋅ 10 –3	0,110 ⋅ 10 –3	0,937 ⋅ 10 –4
20	0,245 ⋅ 10 –4	0,925 ⋅ 10 –4	0,158 ⋅ 10 –3	0,216 ⋅ 10 –3	0,233 ⋅ 10 –3	0,211 ⋅ 10 –3	0,180 ⋅ 10 –3
23	0,429 ⋅ 10 –4	0,162 ⋅ 10 –3	0,277 ⋅ 10 –3	0,378 ⋅ 10 –3	0,407 ⋅ 10 –3	0,368 ⋅ 10 –3	0,314 ⋅ 10 –3

Безусловно, основной особенностью расчетных интенсивностей пыления, выполненных по формуле (1), является отсутствие числового значения при скорости ветра 5 м/с для самой мелкой пыли (срединный диаметр 5 мкм). Данный факт имеет очевидное объяснение: величина пороговой скорости (табл. 2, 3-й столбец, 2-я строка) выше значения динамической скорости (табл. 1, 2-й столбец, 2-я строка), т. е. в рамках данной модели

(схема DEAD) эмиссии пыли такой крупности не происходит. Кроме того, хорошо видно, что при малых скоростях ветрового потока (не более 8 м/с) практически для пыли любой крупности значения интенсивности пыления, рассчитанные по схеме DEAD, несколько выше аналогичных расчетных данных по зависимости Westphal D. L. et al. При величине скорости ветрового потока 11 м/с результаты расчетов интенсивности пыления по обоим используемым подходам наиболее близки. Дальнейшее увеличение скорости ветра (встречается существенно реже) приводит к тому факту, что расчетные (по зависимости Westphal D. L. et al.) интенсивности пыления заметно превышают аналогичные величины, вычисленные с использованием схемы DEAD.

Обобщением расчетных данных табл. 3 и 4 являются кривые рис. 3, а и 3, б , на которых представлены суммарные интенсивности пыления при вариации либо скорости ветрового потока (строго по решаемой задаче), либо расчетной величине динамической скорости на высоте пыления соответственно. Поведение кривых рис. 3, а и 3, б подтверждают указанный выше факт: до величины скорости ветрового потока 11 м/с превалирует кривая интенсивности пыления по схеме DEAD, а при более высокой скорости – кривая по зависимости Westphal D. L. et al. Пересечение кривых происходит вблизи отметки 11 м/с.

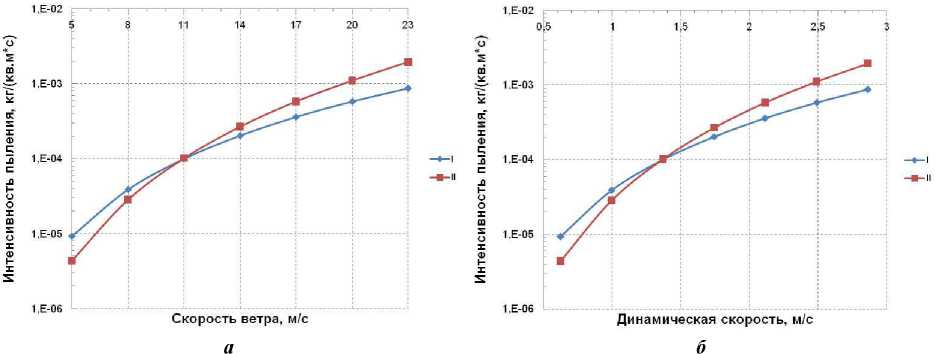
Рис. 3. Расчетные интенсивности пыления в зависимости от: а – скорости ветрового потока на референтной высоте и б – динамической скорости на высоте пыления;

I – схема DEAD (ромб); II – зависимость Westphal D. L. et al. (квадрат)

Естественно, что построенные кривые описываются степенными функциями AV ⁿ в 4-й (зависимость Westphal D. L. et al.) и 3-й (схема DEAD) степенях либо скорости ветрового потока (в рамках решаемой задачи), либо расчетной величине динамической скорости на высоте пыления. Коэффициенты пропорциональности A в степенных зависимостях следующие: для рис. 3, а : I – 8,031 и II – 6,987; для рис. 3, б : I – 3,877 и II – 2,896. Размерность скорости V в обоих случаях м/с.

Расчетные данные интенсивности пыления, представленные в табл. 3 и 4, необходимы при решении конвективно-диффузионного уравнения распространения пыли при описании граничных условий на поверхности пыления. В силу того, что указанное уравнение является линейным, достаточно будет выполнить численные эксперименты по пространственно-временному распределению концентрации пыли в исследуемой области, например, для данных табл. 4 (зависимость Westphal D. L. et al.). Зная соответствующие отношения интенсивностей пыления табл. 3 и 4, получаем значения концентрации пыли, отвечающие эмиссии пылевых частиц по схеме DEAD. В результате прогноз пространственно-временного распределения концентрации пыли будет определяться в некотором диапазоне значений.

Естественно, авторы понимают, что для верификации численной модели необходимо проведение трудоемких экспериментальных исследований на объекте пыления, что, к сожалению, пока не может быть реализовано по целому ряду причин. Тем не менее предпринята попытка проверить на объективность полученные значения интенсивности пыления. Для этого проанализированы данные отчета «Реконструкция хвостохранилища до отметки 200 м: проектная документация. Раздел 8 "Перечень мероприятий по охране окружающей среды"», посвященного реконструкции хвостохранилища АНОФ-2 до высотной отметки 200 м. Специалисты ЗАО "Механобр Инжиниринг" используют показатель – "максимальная удельная сдуваемость пыли". В своих оценках авторы указанного отчета используют значение 5,29 ⋅ 10 ^–6 кг/(м ²⋅ с), что в представленных на рис. 3, б графических зависимостях отвечает значению динамической скорости не выше 0,6 м/с. Представляется возможным сделать два вывода: 1) предлагаемый методический подход достаточно объективен и работоспособен; 2) при высоких скоростях ветрового потока прогнозируемые значения интенсивности пыления будут существенно выше тех величин, которые принимаются проектировщиками в оценках воздействия объектов пыления на окружающую среду.

Выводы

Представлен короткий экскурс существующих подходов по оценке горизонтального и вертикального потоков массы с пылящих поверхностей (пустыни, хвостохранилища и др.), которые необходимы для прогнозирования загрязнения приземного слоя атмосферы на базе численного моделирования.

Более подробно описаны два подхода по оценке интенсивности пыления (зависимость Westphal D. L. et al. и схема DEAD), которые, по мнению авторов, наиболее приемлемы для решения практической задачи о влиянии скорости ветрового потока и высоты пылящей поверхности на загрязнение атмосферы для района г. Апатиты от воздействия близлежащего хвостохранилища АНОФ-2. Оба подхода базируются на функциональной зависимости потока массы от динамической скорости на высоте пыления в 4-й и 3-й степенях соответственно.

Продемонстрирован достаточно простой и нетрудоемкий переход к определению динамической скорости и* и скорости на высоте +10 м над пылящей поверхностью u ₁₀ по данным скорости ветра набегающего потока и высоты дамбы. Указанные величины необходимы для выполнения прогнозных расчетов вертикального потока массы на базе созданной двухмерной численной модели аэродинамики атмосферы исследуемой области.

Выполнен сравнительный анализ расчетных значений поинтервальной интенсивности пыления на базе выбранных подходов при вариации скорости ветрового потока в широком диапазоне. Указан экономичный путь дальнейших численных экспериментов по прогнозу пространственно-временного распределения поинтервальной концентрации пыли, основанный на линейной природе конвективно-диффузионного уравнения и выполненном анализе расчетных вертикальных потоков массы пыли с использованием зависимости Westphal D. L. et al. и схемы DEAD.