Robust Sliding Mode Fuzzy Control of a Car Suspension System

Published Online July 2013 in MECS

The purpose of a car suspension is to adequately support the chassis, to maintain tire contact with the ground, and to manage the compromise between passenger comfort and vehicle road handling, which is important for the safety of the ride. Generally, there are three types of suspension systems, namely, passive, semi-active and active suspensions.

Passive suspensions can only achieve good ride comfort or good road holding since these two criteria conflict each other and necessitate different spring and damper characteristics. While semi-active suspense with their variable damping characteristics and low power consumption, on systems offer a considerable improvement [1-2].

A significant improvement can be achieved by using of an active suspension system, which supplies a higher power from an external source to generate suspension forces to achieve the desired performance. The force may be a function of several variables which can be measured or remotely sensed by various sensors, so the flexibility can be greatly increased.

With rapid advances in electronic technologies [3], the development of design techniques for the synthesis of active vehicle suspension systems has been an active area of research over the last two decades to achieve a better compromise during various driving conditions, [4-9].

Studies have been done based on Linear Gauss Quadratic regulator, such as references [10-12]. Linear Gauss Quadratic method has mature theory base and control algorithm, thus it is widely used in suspension control. It should be pointed out that the design and synthesis of active suspensions can be approached from many ways: Modal analysis, as in [13]; bond graph modeling methodologies, as in reference [14]; fuzzy logic, such as in [15], while each of these approaches can bring some useful perspectives, the present paper will focus on the applications of robust control techniques, and the following work will constitute the trends of the robust system structure and performance potentials.

The aim of this paper is to develop the control algorithms, which can achieve comfort and good handling quality without excessively degrading the body and axle working space.

This paper is organized as follows. In section II, the dynamics of a quarter-car suspension system is explained. Optimal control is designed in section III. Simulations are presented in section IV. At the end, the paper is concluded in section V.

• II.    A Quarter-Car Suspension System

A car suspension system is the mechanism that physically connects the body of the car to their wheels, in other word suspension system isolates the car body from road disturbances and inertial disturbances associated with cornering and braking or acceleration.

Figs. (1, 2) illustrates the quarter–car model of a passenger car that most commonly used for controller design studies of active suspensions [16]. The equations of motion for the car model in the state equation are represented by:

mbzb = fa - ^k1^(z_b - ^zw) - cs^(z_b - ^zw)        (1)

^mw^zw = - fa + ^k1^(z_b - ^zw) - ^k2^(zw - ^zr)

with the following specifications of the suspension system are given in Table 1:

Table 1: quarter car parameters

Parameters	Symbols	Quantities
Body mass	m b	250 kg
Wheel mass	m w	50 kg
Stiffness of the body	K 1	16 kN/m
Stiffness of the wheel	K 2	160 kN/m
Stiffness of the damper	C s	1.5 kN.s/m

To transform the motion equations of the quarter car model into a space state model, the following state variables are considered:

Then the motion equations of the quarter car model for the active suspension can be written in state space form as follows:

• x =	A .x +B. f +F. z ar							(3)
with	"  0	0	1		— 1		■  0  "
A =	0 k 1 — mb k 1 L m w	0 0 k mw	0 cs — mb cs ---- - mw		c 1 s mb c s m w J	■ ,	10 - 1 L - w J
and				" 0 "
			F =

X = [ X„ X2, X3, X4]r                  (2)

where x 1 is body displacement= z b -z w , x 2 is wheel displacement =z_w-z_r, x₃absolute velocity of the body =

• 7                                                 Z ^

• ^zb    , and x 4 absolute velocity of the wheel = ^w .

  

where f a : control force, z r : road input displacement.

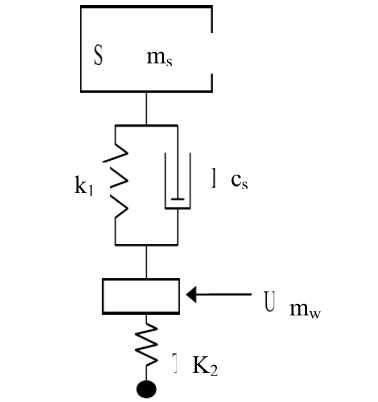
Fig. 2: 2 DOF model

• III.    Suspension Control Development

Fuzzy control systems are rule-based or knowledgebased systems, which have a set of fuzzy IF-THEN rules representing a control decision mechanism to adjust the certain effect coming from the system. Fuzzy controller have succeeded in many practical control problem that the conventional theories have difficulties to deal with. Therefore, the fuzzy control theory was used in this paper. Fig. 3 shows the rule table membership functions of the fuzzy controller.

Fig. 1: quarter car model

NB NS 2E PS PB

Input

NB NM NS 2E PS PM PB

Output

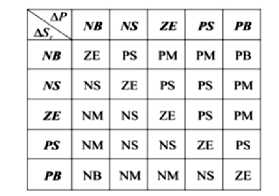
Fig. 3: Membership functions and rule table of fuzzy control

Fuzzy control has been proposed to tackle the problem of car suspension for the unknown environmental parameters. However, the large amount of the fuzzy rules makes the analysis complex. Some researchers have proposed fuzzy control design methods based on the sliding-mode control (SMC) scheme. Since only one variable is defined as the fuzzy input variable, the main advantage of the FSMC is that it requires fewer fuzzy rules than FC does. Moreover, the FSMC system has more robustness against parameter variation. Although FC and FSMC are both effective methods, their major drawback is that the fuzzy rules should be previously tuned by timeconsuming trial-and-error procedures.

Traditional SMC is representing the simpler form of the robust control. Since the system is of the first order, the switching function is selected as:

=  -  ,

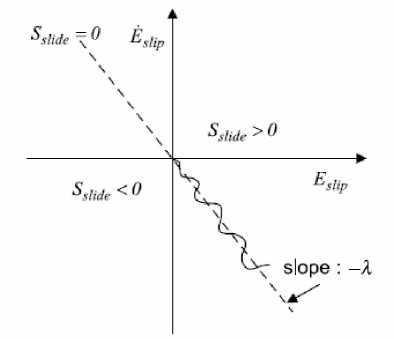
Fig. 4: Phase plane of sliding mode control

Where λ_r is the reference input wheel slip. The sliding motion occurs when state ( , ^̇ ) reaches subspace (a point in this case) defined by s=0 . (see Fig.4 )

The control that keeps the state on the switching subspace is called the equivalent control. Thedynamics in sliding mode can be written as

̇=0

It can be shown that,

S (x,, x2) = x2 + Ax, X > 0

For the convergence conditions:

Ueq = -L '[alX1 + (a2 + X)x2]

where:

a1: –ks/ Ms a2: –bs/ Ms

L: a gain of the control related to Ms

L=√    , bmin: empty vehicle bmax: loaded vehicle

Ug guarantee convergence towards the sliding surface and is defined by following form:

Ug =- L- K .sgn( S )

K is satisfying the sliding condition. When the system state is on the switching subspace, the hitting control is zero. The hitting control is determined by the following reaching condition, where is a strictly positive design parameter:

̇≤-  | |

Assume there are n rules in a fuzzy knowledge base and each of them has the following form:

Rule i: if s is S i the u is α i +β i s

Where u is the output variable of the fuzzy system; S are the membership functions and ( α i ,β i ) are singleton control actions. By the method of center of gravity:

∑     (  +   )

=            ⧸∑

where w_i is the firing weight of the i^th rule, α=[α₁, …., α n ]^T, and β =[β 1 , …., β n ]^T

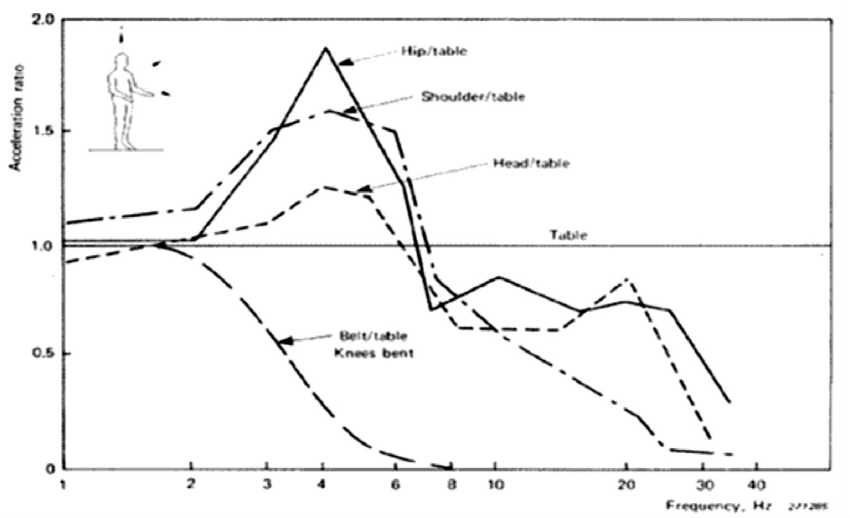
Fig. 5.a: Transmissibility of vertical vibration from table to human body, [17]

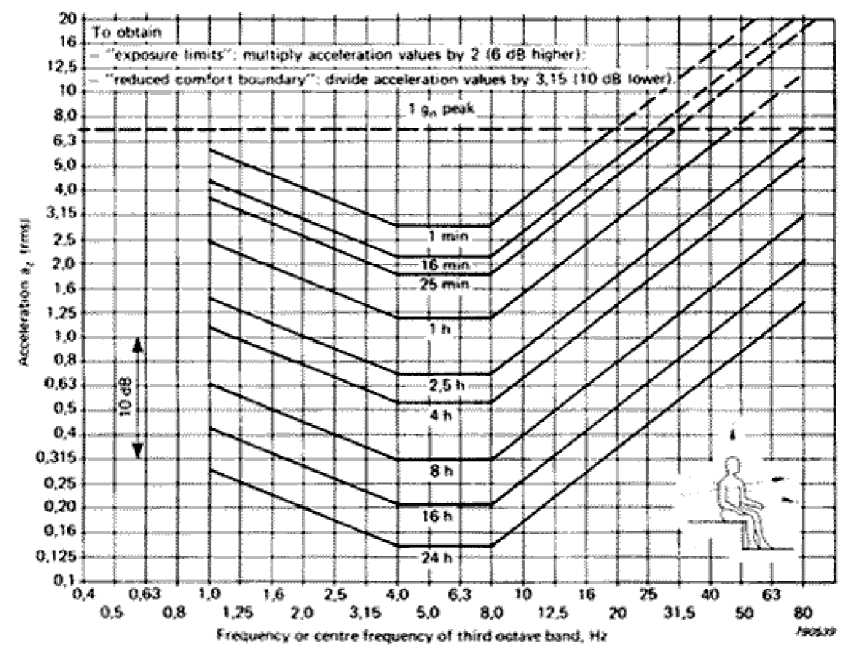
Fig. 5.b: Vertical vibration exposure criteria curves, [17]

• IV.    Simulation Results

The mathematical model of the system and the proposed sliding mode controller as defined in previous equation were simulated on computer by using the MATLAB and SIMULINK software package.

Fig. 3a shows the suspension travel of both the active and passive suspension systems due to a step dump for comparison purposes. Fig. 6 illustrates clearly how the active suspension can effectively absorb early the vehicle vibration at 1.6 sec. while the passive system absorb at 2.25 sec. Moreover the wheel deflection is also smaller in the active suspension system.The body acceleration in the active suspension system is reduced significantly, which guarantee better ride comfort. The corresponding controller effort is illustrated at Fig.7.

Another common road inputs model assumed that the vehicle is to travel at a constant forward speed over

• i)    A random road profile, which is approximated by an integrated white noise input.

• ii)    the road profile w (t) representing a single bump that acts as disturbance, given by cosine function:

w_(t     ∝ (1+соѕ8 nt )×0․5   ti ≤ t ≤ t₂

()={0                   otℎerwise

Where α is the height of the bump, t₁ and t₂ are the lower and the upper time limit of the bump. Figure 8 shows the bump height for 10 cm.

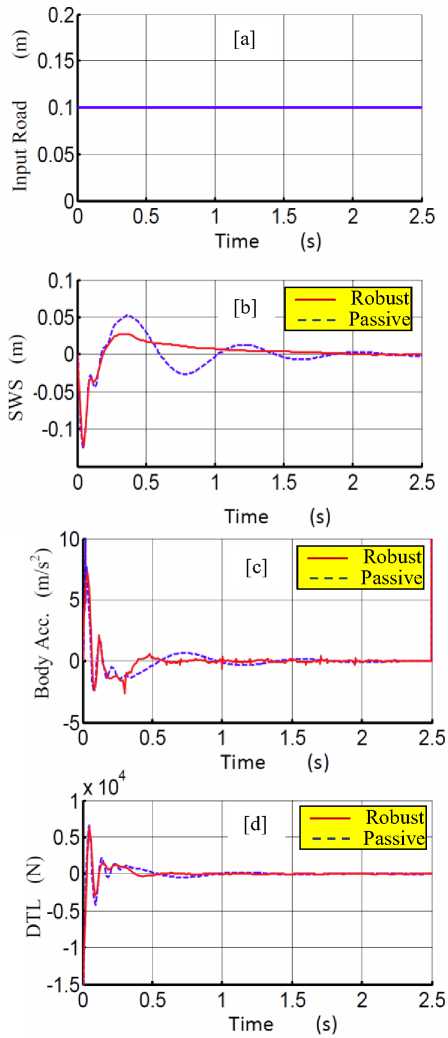
Fig. 6: The response of the suspension system with passive and robust Fuzzy control systems on smooth road

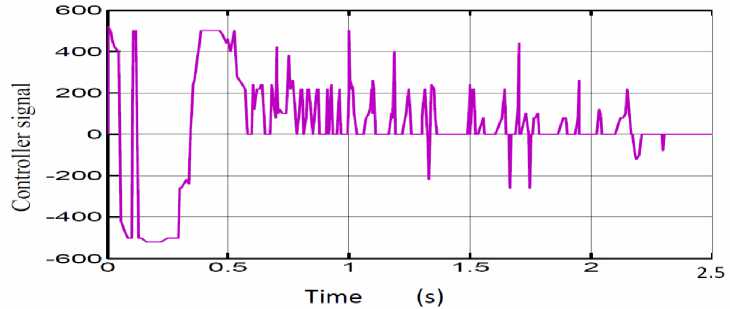
Fig. 7: Fuzzy control signal for smooth road

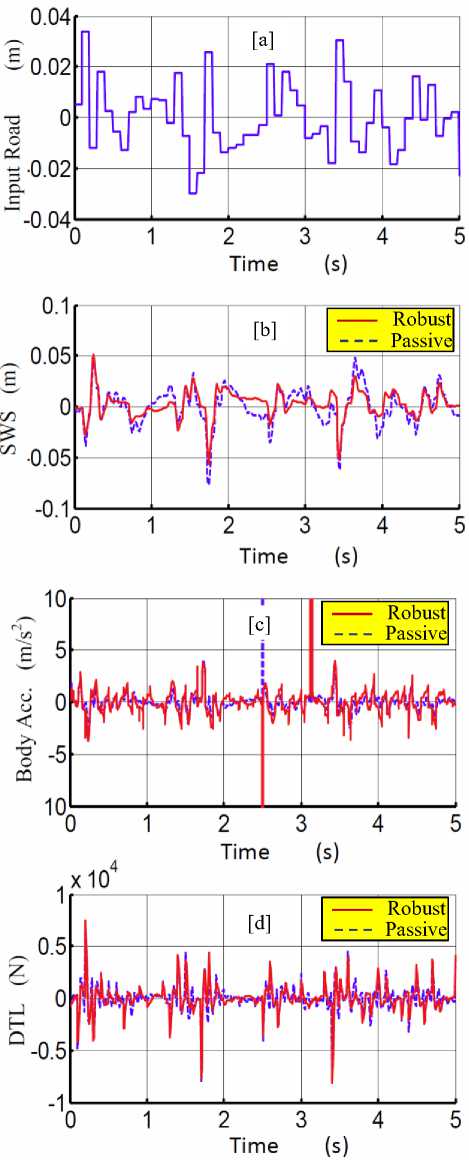
Fig. 8: The response of the suspension system with passive and robust Fuzzy control systems on real road roughness

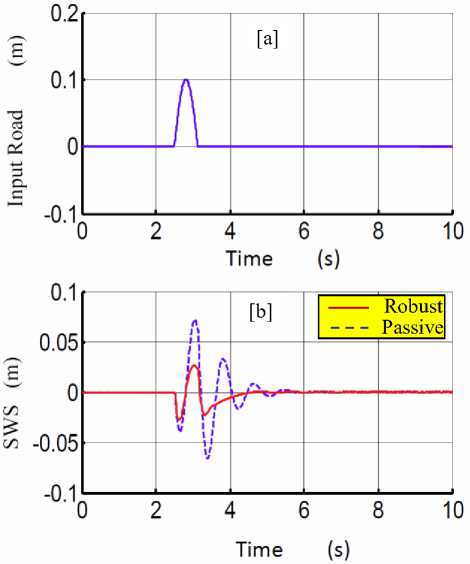
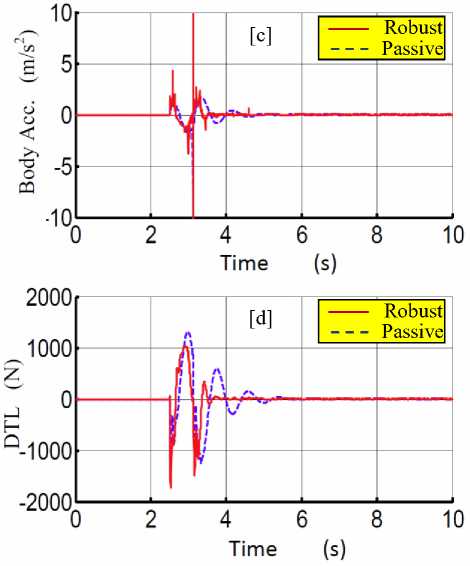
Fig. 9: The response of the suspension system with passive and robust Fuzzy control systems on cosine road profile

In Figs. (8,9) the results confirm the robustness of the proposed designed controller with the different road conditions. Therefore it is clear that the active suspension system improves the ride comfort while retaining the road handling characteristics, compared to the passive suspension system.

• V.    Conclusion

Many different control methods for suspension have been developed and research on improved control methods is continuing. Most of these approaches require system models, and some of them cannot achieve satisfactory performance under the changes of various road conditions, while soft computing methods like fuzzy control don’t need a precise model.

Computer simulations are performed to verify the feasibility of the proposed sliding mode fuzzy controller for the active suspension design by comparing with the passive suspension system. Based on simulation, it can be concluded that the sliding mode fuzzy control of active suspension system performs well as it is preferred to passive suspension system. This designed control is simple and easy to implement.