Robustness Analysis of Layered Public Transport Networks Due to Edge Overload Breakdown

Published Online February 2014 in MECS

Many transport networks have already been investigated with concepts of statistical physical of complex networks [11]. These networks are called public transport networks, in which the nodes are the stations of public transport networks and the edges are the links connecting nodes along the route. These public transport networks can be defined as railway networks [12][13], airport networks [14][15], subway transport networks [16-18] and bus-transport networks [19][20]. Urban bus transport system can be abstract as complex network composed of bus stations and bus lines [21], so we can analysis it with the methods of complex networks. The robustness of the public bus-transport network is an important measurement of the urban transportation performance; it has a great deal of theoretical significance and practical significance to research on it. Von Ferber etc. [22] used different attack strategies to the bus-transport networks of 14 cities; these networks may exhibit scale-free behavior. They focused on the influence on the characteristics of public transport networks after removal of the nodes. Through simulating different attack strategies they elaborated vulnerability criteria allow to find the minimum removal strategy to achieve maximum damage effect on these systems. Mirko Scha¨fer etc. [23] proposed a proactive measure to enhance the robustness of heterogeneously loaded networks against cascades of overload failures. It is based on load dependent weights and uses each shortest flow path to assign more homogeneous load on nodes and edges to enhance the networks robustness and at the same time reduce the investment costs.

All the research mentioned above achieved important results on robustness of complex networks. But in terms of most of the research on robustness of complex networks, on one hand, they considered the networks as distinct object, but in fact most of them are only a part of large systems with layered structure, and these coexisting topologies interact and depend on each other. For instance, in a layered transport network, the nodes in the lower layer are the stations in the transport networks while the edges are the existing lines connecting neighboring stations. In the upper layer, the nodes also represent the stations in the transport networks, but the definition of the edges is different. The edges in the upper layer connect the first and the last station in a particular route. The lower layer describes the physical infrastructure in the transport networks, it is also called physical layer. At the same time, the upper layer describes the traffic flows in the physical layer, it is also called logical layer. A logical network composed by traffic demands maps into the physical network composed by physical infrastructures [24][25]. In a layered network, the topological structure of every layer maybe different, so its robustness changes along with the network structure due to different attack strategies. On the other hand, the traditional researches on the cascading failures focus mostly on the static failures of nodes (edges) without consideration of the load on the nodes (edges). In fact, most of networks have load, and the load on the networks is dynamical. When the structure of the network changes, such as adding new nodes (edges) or removing nodes (edges), the load of the network will be redistributed [10][26][27][28]. The redistribution of the load may lead to cascading failures even the collapse of the whole network.

Cascading failures refer to the subsequent failure of other parts of a network induced by the failures of or attack on only a few nodes (or edges). It can occur in many physical systems. Evidence has shown that locally emerging cascading failures in networks can influence the entire network, often resulting in large-scale collapse in the network. For example, the largest blackout in US history took place on 14 August 2003 due to failure in the power grid and breakdowns of the internet. A number of aspects of cascading failures in complex networks have been discussed in literature. However, in the research of the cascading failures, most works paid close attention on the breakdown triggered by nodes in single network, the failures triggered by edges in layered networks are also significant for the network security, it is worthwhile to investigate it.

This paper proposes a model of cascading failures with the removal of the edge with the highest load and researches the robustness of layered bus-transport network composed of space P layer and space L layer in three major cities of China. In space P, the nodes represent the bus stations, and an edge connects two bus stations when at least one bus route provides service. In space L, the nodes also represent the bus stations, but an edge exists between two bus stations only if they are the consecutive stations on at least one bus route. We take the space P as logical layer and the space L as the physical layer, and then we obtain a layered bustransport network. We find that in the layered bustransport networks, the traffic flow of logical layer can be mapped on the physical layer and affects the load distribution of physical layer, as the result the edges of physical layer have different load.

In this letter, we remove the physical edge which has the highest load, and because of the load of the removal edge will be redistributed to its neighbor edges. After one neighbor edge receives additional load, its total load may beyond its capacity and trigger the failure of this edge. This process is repeated until there are no overloaded edges. It will even lead to collapse of the entire network. Through research of the avalanche size caused by removal of the edge with the highest load we can analysis the robustness of the layered bus-transport network. Our research will apply basis for further management and optimization of urban public traffic networks.

The organization of this paper is as follows. In the next section, we will describe the layered bus-transport network model in details and propose the method of redistribution of load. In the section 3, the results of the simulation of cascading failures are provided and discussed by measuring the public bus-transport networks in three major cities. Finally, section 4 presents our conclusions.

• II.    The Layered Model and Method of Redistribution

• 2.1    The Model of Layered Bus-Transport Network

The multilayer structure is well researched in the computer networks. In the two-layer model, the lower layer is called physical layer while the upper layer is called logical layer. The upper layer can mapped onto the lower layer. For example, in the computer communication network, the network is composed of two layers: the IP layer and the optical layer (such as cables and optical fibers) [29]. The IP layer is mapped onto the optical layer. Though the topology of each layer is different, the lower layer provides service for the upper layer while the traffic flow in the upper layer is undertaken by the lower layer.

Similarly, it is convenient to view a public transport network as a two-layer network like computer communication network. In a layered public transport network, the physical layer represents the physical infrastructures while the logical layer represents the traffic flow on the infrastructures. For instance, in a layered railway network, the nodes in the physical layer represent the stations and the edges are the existing rail tracks connecting neighboring stations. The nodes in the logical layer also represent the stations while the edges represent the connection between the first and the last station of a particular train route. This layered framework allows us to study the relation of traffic infrastructures and traffic flow and the robustness due to cascading failures [24][25].

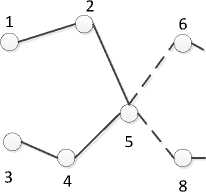
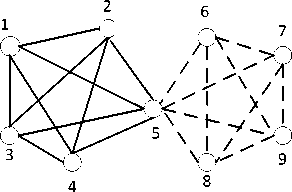
We focus our research on the bus-transport network, so we can use the theory mentioned above to establish a layered model for the urban public bus-transport networks. To our knowledge, an urban bus-transport network can be mapped into two spaces: space P and space L [30-32]. In both spaces, nodes have the same meaning, they represent the bus stations. But the definition of edges is different. In the space P, an edge connects two nodes when at least one bus line or one bus provides service between these two bus stations. In the space L, an edge between two nodes exits only if they are consecutive stations on at least one bus line. Fig.1 is a simple description of space P and space L. s1~s9 represent the stations, the dashed line and solid line represent two different bus lines.

a

b

Fig. 1: The description of the bus-transport network

In the Fig.1, The subgraph (a) describes space L while the subgraph (b) describes space P. We can see that in a network with two bus lines, there are more edges in the space P than in the space L.

With the idea mentioned above, we may think that space P describes a kind of traffic flow while space L represents the information of the bus lines, which is the physical infrastructure of the flow [33][34]. In fact, because of space L does not contain the case that two buses may run the same road but not share all their stations, it can’t describe the road network exactly. But due to it can draw most of the roads, so here we can use it to represent the road network. To construct a two-layer network for the bus-network, we take space P as the logical layer and space L as the physical layer, and then we establish a layered urban public bus-transport network which will help us to analysis the robustness of public transport network due to cascading failures.

• 2.2    The Method of Load Redistribution

In the two-layer model, the edges of both layers can have weights assigned to them and denoted by

w (.) with w = 1 for unweighted network. Every logical edge e ^λ = ( µ ^λ , ν ^λ ) is mapped on physical layer as a path M ( e ^λ ) connecting the node µ ^φ and ν ^φ in the physical layer, corresponding to the node µ ^λ and υ ^λ in the logical layer. We set the load of an edge e ^φ in the physical layer as the sum of weights of all logical edges whose paths traverse this edge ^[35].

l ( e ^φ ) = ∑ w ( e ^λ ) (1) e ^λ : e ^φ ∈ M ( e ^λ )

The load on an edge can be seen as the traffic flow traverse over it. Here we consider space P and space L as unweighted networks, so the load of edge e ^φ in the physical layer is actually the total number of edges in the logical layer which are mapped over the edge e ^φ , and we assume this load to be the initial load of edge in physical layer.

In the physical layer, when an edge e connecting the node i and j is attacked or random failure, the load on it will be redistributed to the neighboring edges connecting to the ends of the edge eij . In the actual public bus-transport networks, an edge broken will trigger the broken of the edges which are belong to the same bus line with the broken edge. Here we just consider the case that all the neighbor edges of the broken edge can receive additional load which is redistributed by the broken edge.

The additional load received by any a neighbor edge e is proportional to its initial load ^[36-38].

ЛL. = L L /(У L +У L Л (2)

im      ij im ^ < v а сГ i ^ia / 4 b cr j ^jb

Where e is the attacked edge, L represents the load on the edge e_y , Г. represents the set of neighbor nodes of the node i while г . represents the set of neighbor nodes of the node j . Л L_t is the initial load received by edge e .

Once an edge in one network is broken after it is attacked or random failure, if the load on this edge is relatively low, when the load is redistributed the neighbor edges will also receive low additional load. After receive the additional load, the total load on one of the neighbor edge may not exceed its capacity, and this case will not trigger cascading failures. But if the load on the edge which is attacked or random failure is relatively high, after the neighbor edges receive the additional load redistributed from the broken edge, its total load may exceed its capacity. This case will result in the further distribution of the load and may trigger cascading failures of the whole network. Fig.2 illustrates load redistribution of an edge e after it is attacked or random failure.

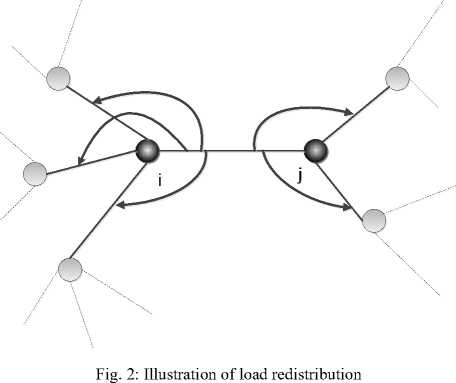
edges connecting to both ends of the edge e as showed in the figure. Among these neighboring edges, edges with high initial load will receive more additional load. If the total load on a neighboring edge after it receives the additional load exceeds its capacity, it will be broken.

If we don’t take into account the cost, the cascading failure can be avoided by assigning extremely high capacity to edges. However, we must consider the cost in the actual situation, because the cost is too high we can’t assign enough capacity to the edges, so the capacity is limited by cost. In the Motter-Lai ^[26][39] model, for the case of cascading failure caused by the broken of the nodes, the capacity of a node is proportional to its initial load. In the case of cascading failure caused by the broken of the edges, we use C to represent the capacity of the edge e . For simplicity, we assume the capacity is proportional to the initial load of the edge, and then we can rewrite the equation for the edges in the following form.

Cij = (1 + а) Lij, i, j = 1,2......N              (3)

Where а >  0 is a control parameter which represents the additional cost that is needed to deal the additional load and to protect the edges. Due to the limitation of capacity of every edge, for one of the neighbor edge, if the expression L_im + Л L_im >  (1 + а ) L_im is true, then the edge can’t undertake the additional load and it will be broken. This case will lead the load on the broken edge redistribute to the neighboring edges and may trigger the broken of other edges. Only if all the loads on the edges are lower than its capacity, the cascading process ends.

We focus on the effect on the whole network caused by attacking only one edge of the network. At first we remove an edge in the physical layer, and here we choose to remove the edge with the highest load. To measure the robustness of the network and the avalanche size caused by attacking the edge e , we use S to represent the number of the invalid edges in the physical layer. It is obviously that 0 < S.. < N -1 , where N represents the total number of nodes. To quantify the effect on the whole network, we adopt the normalized avalanche size.

S

^     Z-^ ij c A i^j

" (Na (N -1))

In the Fig.2, when an edge e is attacked or random failure, the load on it is redistributed to the neighboring

Where, A and N respectively represent the set and the number of the attacked edges.

Obviously, the smaller the value of the avalanche size S , the stronger robustness of the whole network due to cascading failures. If the control parameter α is large enough which means that each edge has enough power to deal with the additional load, then the removal of any edge will not lead to cascading failures. So there is a critical value α , as α ≥ α , the cascading failure will not appear, the network keep its function. When α < α , the broken of some edges will trigger the whole network collapse. Here α is an important parameter to measure the robustness of the network; it represents the minimum value of the capacity of an edge to avoid cascading failures. Obviously, the smaller is the value of α , the stronger robust is the network.

• III.    Simulation and Analysis

In the process of the actual transportation of people's daily life, the congestion of some sections of the bus line will diffuse to their neighbor sections. As mentioned above, in the Load-Capacity model of edges, every edge has a load capacity, when the load on it exceeds its capacity, cascading failures may appear in the network which will result in the collapse of the whole network. In the research of public bus-transport network, we introduce a model which considers the congestion on the bus line and the Load-Capacity of edges.

To verify our model, we choose the public transport network of three major cities in China. The cities are Beijing, Shanghai and Hangzhou. The data of these three networks are showed in Table.1.

Table 1: The data of public bus-transport networks of three major cities in China

City SN RN AS AL Beijing 7864 1308 27.51 4.55 Shanghai 5931 842 22.52 3.38 Hangzhou 2750 509 20.34 4.19 normalized avalanche size S to measure the robustness of the networks.

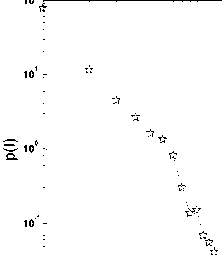
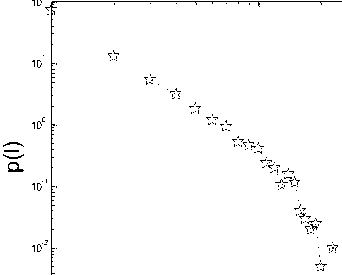
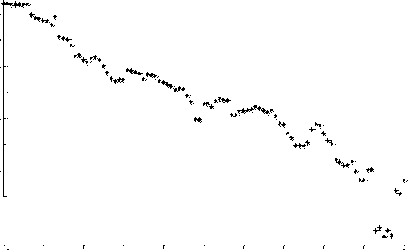
Before we simulate the effect of removal the edge with the highest load on the whole network, we try to predict what will happen by studying the load distribution in the physical layer. The load in the physical layer is an important parameter to research the cascading failures in the network. Obviously, the higher the load on an edge in the physical layer, the more it destroyes the network when it is removed. If the load is distributed evenly, the removal of the edges may not trigger cascading failures. But if the load is distributed very unevenly, the removal of the highly loaded edges will cause the whole network to be damaged. In Fig.3 we present the load distribution in three layered public bus-transport networks we studied. In each case, the load distribution is right-skewed. This means that there are some edges in the physical layer which carry higher load than others, so removal of these edges will affect the whole network.

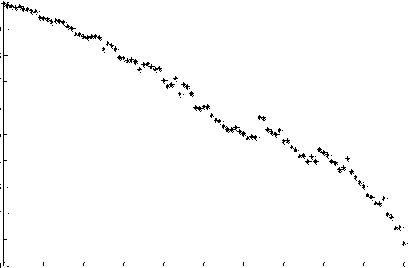
Next, we simulate cascading failures after removal of the edge with the highest load. Fig.4 shows the avalanche size of physical layer of three transport network with different control parameter. From this, we can indicate that a bigger control parameter corresponds to a stronger bus-transport network.

Load l

10-2 100

data1]

(a)

In the Table 1, SN represents the total account of stations; RN represents the total account of bus lines. AS represents the average number of stations belongs to one bus line. AL represents the average number of bus lines which traverse the same bus station.

We map these three public bus-transport networks on space P and space L respectively, and then we can obtain layered networks in which the logical layer is space P while the physical layer is space L. As mentioned above, the load on an edge in the physical layer is represented by the total weights of the edges in the logical layer which are mapped onto it. We focus on the cascading failures caused by removal of the edge with the highest load in the physical layer and adopt the

(b)

₁₀-3 10⁰

Load l

(c)

Fig. 3: The load distribution in three cities. (a) The load distribution of city Hangzhou. (b) The load distribution of city Shanghai.

(c) The load distribution of city Beijing

( и    data1 J

0.99

0.98

0.97

0.94

0.93

0.92

0.91

0.96

(Л

0.95

0      0.1      0.2     0.3     0.4     0.5     0.6     0.7     0.8     0.9      1

α

(c)

Fig. 4: The simulation result of three cities.

(a) The normalized avalanche size in city Hangzhou.

(b) The normalized avalanche size in city Shanghai.

(c) The normalized size in city Beijing

0.9

From these figures, we indicate that with the increase of the control parameter, the avalanche size decrease after removal the edge with the highest load. But because edge with more load than others exists in these networks, so removal of it bounds to cause the cascading failure of the network.

0.99

0.98

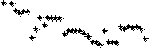
0.97

0.96

0.95

0.94

0.93

0.92

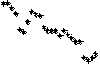
0.2     0.3     0.4     0.5     0.6     0.7     0.8     0.9       1

(a)

0.995

0.99

0.985

0.98

0.97

0.965

0.96

0.955

(Л

0.975

0.6     0.7     0.8     0.9      1

0      0.1      0.2     0.3     0.4     0.5

α

(b)

0.95

• IV.    Conclusion

In urban public bus-transport network under the condition of high load and easy to appear emergencies, how to effectively improve the robustness of urban public transport network is a problem need to be urgently solved. The failure of some sections of the line causes the increase of the load of other sections, potentially make other sections to be overload and influence their functions.

With the redistribution, the failure diffuses to the whole network and leads to more damages. This will reduce the capacity and efficiency of the urban public bus-transport network.

In the layered public bus-transport network, the physical layer undertakes the traffic flow of the logical layer as the load of its edges. In the physical layer, the sections with high load may exceed their capacity, this will lead them to be broken and lead to the redistribution of their load to the neighbor sections. After the neighbor sections receive the additional load, if the total loads beyond their capacity, it will trigger more edges to be broken. The traffic flow in the logical layer affect the load distribution of the physical layer, if we can properly increase the capacity of the road, it will reduce the probability of cascading failure of the transport network. So it has a realistic significance to study the robustness of the layered public transport network.

Acknowledgement

The work is supported by the National Natural Science Foundation of China under Grant No. 61374152, the commonweal application technique research project of Zhejiang Province under Grant No. 2012C23126.