Роль делокализации атомов в процессе размягчения стеклообразных твердых тел

Ранее было развито представление о наличии взаимосвязи между условием стеклования жидкостей и критерием плавления кристаллов [1, 2]. В данном сообщении приводятся результаты, полученные в последние годы по этому вопросу.

Предполагалось [2], что как при температуре плавления кристалла, так и при температуре размягчения стекла под действием теплового давления происходит критическая деформация межатомной связи (ее возбуждение). Недавно экспериментально установлено [3], что при температуре плавления полиэтилена межмолекулярные связи растянуты до предельной величины, что подтверждает нашу гипотезу. Элементарным актом размягчения стекла – процесса, обратного стеклованию жидкости, – служит предельная упругая деформация межатомной связи, соответствующая максимуму квазиупру-гой силы [2]. Критерием перехода стекло-жидкость может служить отношение энтальпии предельной деформации межатомной связи ∆H e к средней энергии теплового движения частиц при температуре стеклования T g

д =ДНе, где k – постоянная Больцмана.

В модели возбужденного состояния [1, 4] предельная упругая деформация межатомной связи ∆r_m интерпретируется по другому как смещение частицы на критическое расстояние ∆r m , соответствующее максимуму силы притяжения между атомами (рис. 1). Кинетическая единица (атом, группа атомов), способная к критическому смещению, называется возбужденным атомом, а сам подход – моделью возбужденного состояния. Рождение возбужденного атома обусловлено флуктуационной перегруппировкой соседних частиц и носит энтропийный характер. В данной модели величина ∆H e рассматривается как энтальпия возбуждения атома. В качестве возбужденного атома в силикатных стеклах и их расплавах выступает мостиковый атом кислорода в мостике Si-O-Si. Его флуктуационное критическое смещение перед переключением валентной связи [5] представляет собой «процесс возбуждения атома», с которым тесно связана предельная упругая деформация участка кремнекислородной сетки (рис. 2).

Доля флуктуационного объема f = ∆V e /V, образованного за счет критических смещений кинетических единиц из равновесных положений (∆V e = N e ∆ν e ), является функцией давления и температуры

[1, 4],

1 —Si-O	1 -Si-	1 — Si —	о	1 — Si— —	1                                                              1 Si О Si
			p		о	о
-Si-O	-Si-	—Si —	о	— Si —	-Si —C	Si—
а	1	1	6	1	e	1

Рис. 2. Схема переключения мостиковых связей Si-O-Si в силикатных стеклах [5]. ∆rm – критическое смещение возбужденного мостикового атома кислорода перед переключением мостиковой связи

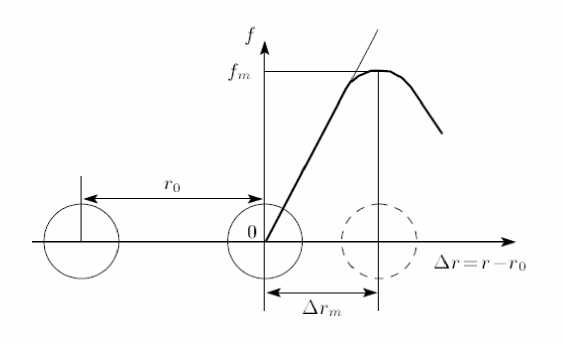
Рис. 1. Схема возбуждения атома (межатомной связи). r0 – равновесное межатомное расстояние, fm – максимум силы притяжения между атомами, соответствующий критическому смещению возбужденного атома ∆rm

f = ( ^Д1^ > СЭСр f — ^J-^¹^ tf \,                    (2)

V u /     V     kT J где ∆νe ≈ c∆rm – элементарный флуктуационный объем, необходимый для реализации предельной деформации межатомной связи (для возбуждения атома), ∆εe – энергия возбуждения атома, ν = V/N – атомный объем, Ne – число возбужденных атомов, с – постоянная. Способы расчета fg = f(Tg), ∆νe и ∆He приводятся в работе [4].

Полагая независимость параметров ∆ ε e , ∆ ν e и f g от температуры T g и давления p стеклования, из уравнения состояния (2) для зависимости T g от давления p получаем выражение

dp = ^J211£1>_PjlK2 .                      (3)

Энтальпия процесса возбуждения атома ∆ H e равна работе, совершаемой против максимального внутреннего p i и внешнего p давлений (∆ ε e = p i ∆ ν e )

∆ H e = ( p i + p )∆ ν e = ∆ ε e + p ∆ ν e .                                       (4)

Эта формула по внешнему виду совпадает с известным уравнением Клапейрона–Клаузиуса для фазовых переходов dp zz At?

dT Tte в котором отношение скрытой теплоты фазового перехода ∆q к температуре перехода Т равно энтропии фазового перехода ∆S = ∆q/T. По аналогии отношение

в равенстве (5) мы назвали энтропией квазифазового перехода стекло-жидкость. Из сравнения соотношений (1) и (7) критерий размягчения стекла (1) приобретает смысл относительной энтропии ква-зифазового перехода g = ∆Se/k                                             (8)

Величину g можно выразить соотношением

^S. — кТ_а In (Дк_г/ fy v) _ In

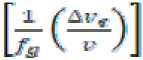
kTs кгв

Отношение объемов ∆ ν e / ν связано с параметрами потенциала Mu ( И = - A r^-m + B r^-n) [6]: ∆ ν e / ν

9/mn, где произведение mn оказывается однозначной функцией коэффициента Пуассона μ [7]. С уче- том этих соображений для оценки q приходим окончательно к формуле

S — In

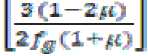
где полагаем, что μ < 0,5.

У стеклообразных систем различной химической природы значения q колеблются в узких пределах около q ≈ 3

У = ^^ * const * 2.5-t- 3.5                  (10)

У стекол определенной группы величина q оказывается постоянной. В качестве примеров в табл. 1 и 2 приводятся результаты расчета q по формуле (9) для сульфатно-фосфатных (q ≈ 3.4) и калиевобо-ратных (q ≈ 2.8) стекол. Для щелочносиликатных стекол величина q равна q ≈ 3, для халькогенидных стекол As-S при разных содержаниях As и S имеем q ≈ 2.8–3.3, а у металлических стекол – q ≈ 3.0 – 3/2. У органических аморфных полимеров значение q заметно ниже среднего значения: q ≈ 2.5. Если выше температуры Дебая среднюю энергию тепловых колебаний решетки, отнесенную на атом, принять равной 3 k T, приведенный выше результат можно сформулировать следующим образом: стекло размягчается, когда средняя энергия теплового движения решетки 3 k T_g становится равной или больше работы предельной упругой деформации межатомной связи 3 k T g ∆ H e .

Таблица 1

Доля флуктуационного объема f g , коэффициент Пуассона μ и параметр q для сульфатно-фосфатных стекол NaPO 3 -RSO 4 (R = Zn, Li, Na, K)

RSO4, мол.%	T g , K	f g	µ	∆ ν e , Å3	ΔHe , кДж/моль	q
NaPO 3	523	0.016	0.294	16	15	3.4
ZnSO 4 10	493	0.018	0.288	12	13	3.3
20	505	0.019	0.284	12	14	3.3
30	510	0.020	0.273	11	14	3.3
40	515	0.020	0.259	10	14	3.3
LiSO 4 10	451	0.014	0.300	13	13	3.5
20	447	0.013	0.303	14	13	3.5
30	429	0.014	0.304	12	12	3.5
Na 2 SO 4 10	496	0.016	0.299	14	14	3.4
20	493	0.016	0.292	15	14	3.4
30	490	0.015	0.288	17	14	3.5
K 2 SO 4 10	444	0.013	0.316	16	13	3.5
20	453	0.014	0.316	15	13	3.4

Таблица 2

Параметры модели возбужденного состояния для калиевоборатных стекол К 2 О-В 2 О 3

К 2 О , мол.%	T g , К	µ	f g	Δv e , Å3	ΔHe, кДж/моль	q
0	578	0.262	0.034	20	13	2.8
1.1	582	0.292	0.034	16	13	2.6
2.5	588	0.293	0.0333	15	13	2.7

3.9	597	0.293	0.032	14	13	2.7
8.5	623	0.293	0.030	13	14	2.8
13.0	658	0.295	0.030	13	15	2.8
18.0	685	0.301	0.029	13	16	2.8
22.8	711	0.295	0.028	13	16	2.8
28.2	723	0.288	0.027	12	17	2.9
33.5	706	0.303	0.026	11	17	2.9

Недавно Магомедов [8] предложил подход, согласно которому элементарным актом процесса плавления кристаллов является делокализация атома, а причиной плавления – резкая делокализация определенной доли атомов решетки. Оказывается, что при плавлении изменение энтропии практически постоянно для определенных групп веществ [8, 9]. Для «рыхлых структур», у которых коэффициент упаковки атомов не превышает Kp ≈ 0.6, изменение энтропии при плавлении составляет [8]

—-— == const =ь 3.S к что совпадает с изменением энтропии при квазифазовом переходе стекло-жидкость (10).

Доля делокализованных атомов при температуре плавления T m также постоянна и составляет око-

ло [8]

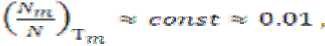
что по порядку величины совпадает с долей возбужденных атомов, размороженных при температуре размягчения стекол [10],

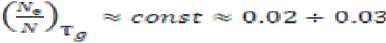
По физическому смыслу процесс делокализации атома [8], на наш взгляд, фактически совпадает с указанным выше процессом критического смещения атома из равновесного положения [1-4], которое трактуется как его возбуждение. В свою очередь возбуждение атома означает возбуждение межатомной связи – ее предельную упругую деформацию, соответствующую максимуму силы притяжения между атомами.

Таким образом, приведенные выше данные можно рассматривать как дополнительные аргументы в пользу развиваемой идеи о том, что размягчение стекла обусловлено плавлением локальных микрообластей структуры – ближнего порядка; элементарные акты переходов кристалл-жидкость и стекло-жидкость в первом приближении имеют общую природу [1, 2, 11]. Они обусловлены делокализацией (возбуждением) определенной доли кинетических единиц решетки – в кристаллах, квазирешетки – в стеклах (рис. 2).