Роль континуального поглощения паров воды в окне прозрачности атмосферы Земли

(1 - A ) S ₀/4 = eo T ⁴,

где          A = 0,3 ± 0,01 – альбедо Земли, которое определяется как отношение восходящего и нисходящего потоков излучения и характеризует долю излучения, отраженного поверхностью Земли и рассеянного атмосферой и облаками;

S ₀ = 1 376 Вт/м² – солнечная постоянная (поток излучения от Солнца на верхней границе атмосферы);

e = 0,62 - коэффициент излучения атмосферы (определяет парниковый эффект);

Т = 288 К – средняя температура Земли;

о = 5,67 10-8Вт/(м2К4) - постоянная Стефана - Больцмана.

Из приведенной выше формулы следует, что при изменении солнечной постоянной, либо альбедо Земли, либо коэффициента излучения произойдет изменение температуры поверхности Земли. Расчеты показывают, что возрастание концентрации углекислого газа вдвое приводит к изменению восходящих потоков излучения примерно на 3 Вт/м2 и к возрастанию средней температуры Земли примерно на 1 oC. Однако более точные оценки чувствительности климата к возрастанию концентрации парниковых газов, полученные на основе моделей общей циркуляции, составляют величину 2,0–4,5 °С [4]. Неопределенность этих оценок обусловлена проблемами учета обратных связей. Так, например, без учета обратных связей удвоение концентрации СО2 приведет к возрастанию температуры Земли примерно на 1,2 оС, а с учетом положительной обратной связи (при возрастании температуры увеличивается концентрация паров воды) прирост температуры удвоится.

Водяной пар является основным поглощающим газом в атмосфере Земли, но зачастую его не относят к парниковым газам, так как возрастание его концентрации происходит опосредованно, через обратные связи. Причем, наряду с положительными обратными связями, имеются и отрицательные обратные связи, которые уменьшают эффект нагрева земной поверхности. Наибольшую сложность в настоящее время вызывает описание облачно-радиационных связей, тогда как обратные связи между потеплением климата и содержанием паров воды и изменениями вертикального градиента атмосферы описываются неплохо.

Несмотря на вышесказанное, современные модели переноса радиации в безоблачной атмосфере еще далеки от совершенства, в первую очередь это касается поглощения парами воды. Так, например, согласно оценкам, приведенным в нашей работе [5], погрешности в нисходящих потоках теплового излучения, обусловленные неопределенностями в коэффициентах континуального поглощения, составляют величину ~2–3 Вт/м2, которая сопоставима с эффектом удвоения СО2 в атмосфере Земли.

В настоящее время сложилась парадоксальная ситуация, когда модели, полученные на основе данных натурных наблюдений, противоречат данным лабораторных измерений. Во-первых, разброс экспериментально измеренных коэффициентов континуального поглощения составляет 10–20 %, что может приводить к большим погрешностям в потоках длинноволновой радиации [2]. Во-вторых, согласно [13] модель континуального поглощения MTCD2.4 достаточно неплохо описывает данные натурных измерений. С другой стороны, наши оценки показывают, что уточнение этой модели на основе современных высокоточных лабораторных экспериментов [6] приведет к тому, что данные натурных измерений будут описываться хуже.

Целью работы является сопоставление моделей континуума, используемых в задачах переноса излучения в окне прозрачности атмосферы 8–12 мкм, а также разработка методики возможного эксперимента в натурных условиях для уточнения этих моделей.

Окно прозрачности атмосферы 8–12 мкм играет важную роль в радиационном балансе атмосферы. Поглощение атмосферными газами в этом спектральном диапазоне определяется не только тонкой структурой спектров поглощения, но и континуальным поглощением паров воды. В настоящее время существует два подхода к определению континуального поглощения, которые основываются на мономерной [3; 20] и кластерной гипотезах [19; 23], хотя в последнее время преобладает точка зрения о том, что наряду с поглощением мономерами следует учитывать и поглощение димерами, например [16]. Достаточно продолжительное время отрицательная температурная зависимость для окна 8–12 мкм являлась важным аргументом в пользу димерной гипотезы, однако такую же зависимость дает и мономерная гипотеза, причем оценки температурной зависимости совпадают не только качественно, но и количественно. Особенностью континуального поглощения является то, что оно достаточно мало и для его экспериментального исследования необходимы самые чувствительные методы исследования. Наиболее детальные лабораторные исследования проведены для комнатных температур, тогда как в стратосфере такие температуры реализуются лишь для летних условий и для приземных высот. Измерения при низких температурах затруднены вследствие того, что концентрация паров воды экспоненциально падает с понижением температуры.

Для моделирования потоков радиации широко используются эмпирические модели, которые получили название RSB [18], CKD [8], позднее MTCKD по фамилиям авторов, принимавших участие в их создании. Следует отметить, что модель RSB определена только для окна 8–12 мкм. В настоящее время наиболее широко используется модель MTCKD, согласно которой континуум принято определять как разность экспериментально измеренного коэффициента поглощения и расчетного с использованием фойгтовского контура, причем каждая спектральная линия учитывается лишь в интервале ±25 см–1. Таким образом, континуум определяется как сумма вкладов в коэффициент поглощения от далеких спектральных линий, отстоящих от заданного волнового числа на расстояние большее 25 см–1 и как сумма вкладов от ближних линий, обусловленных разностью между реальным коэффициентом поглощения и расчетным с использованием лоренцевского контура. Модель MTCKD – эмпирическая модель, параметры которой определяются путем подгонки к экспериментальным данным. Ее широкое использование обусловлено тем, что она верифицирована к атмосферным измерениям нисходящих потоков излучения в контролируемых условиях [13; 22].

Коэффициент континуального поглощения представляют в виде:

k = k_S + k_f = ( C_S exp(– T_S / T ) n _H2O + C_f n ) p_H2O ,                        (2)

где        n – число молекул воздуха в единице объема;

n_{H O} – число молекул Н₂О в единице объема;

p_{H O} – парциальное давление паров воды;

T_s – параметр, определяющий температурную зависимость коэффициента континуального поглощения в случае самоуширения;

C_s , C_f , T_s – параметры, определяемые из эксперимента.

В настоящее время результаты ряда лабораторных измерений [6; 14; 16] демонстрируют, что современные модели континуального поглощения в микроокнах полос поглощения занижают коэффициенты континуального поглощения, обусловленные уширением воздуха (foreign continuum, C_f ), а в окне прозрачности атмосферы 8–12 мкм завышают обратную температурную зависимость коэффициентов континуального поглощения, обусловленных самоуширением (self continuum, C _s ). В частности, в работах [6; 12] отмечалось, что в модели MTCKD используется слишком сильная температурная зависимость, которая при повышенных температурах приводит к расхождениям, достигающим 50 %.

На основе экспериментальных данных [6] нами были оценены параметры C_s при температуре Т = 296 К и T_s (см. рис. 1).

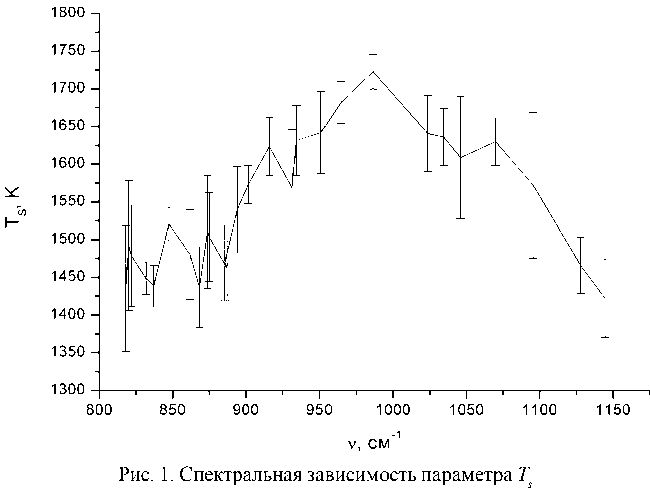
Из рисунка 1 видно, что параметр Т_s меняется в диапазоне 1 500–1 700 К и имеет ярко выраженную спектральную зависимость. Следует отметить, что практически для всех современных моделей этот параметр больше 1 800 К.

О коэффициенте C_f , входящем в формулу (2), имеются противоречивые данные. Как следует из таблицы 1, данные лабораторных измерений [7] коэффициентов у = C f / C s значительно отличаются от модельных. Причем, в современных моделях MTCKD этот коэффициент был уменьшен в сравнении с первоначальными морах [13].

Таблица 1

Отношение коэффициентов C_f / C_s на частоте 950 см^–1

	Burch [7]	RSB [18]	CKD1 [8]	MTCKD1.0
Y = C f / C s	0,005	0,001	0,0014	0,00038

Поскольку параметр C_f определяется с большой неопределенностью, то из экспериментальных данных его температурную зависимость определить не представляется возможным. Поэтому для этих целей мы использовали приближение лоренцевских крыльев линий. В этом случае коэффициент поглощения, обусловленный уширением воздуха, описывается формулой:

k f = Cf- exp

-

V

-

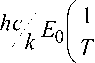
T 0

\I            \//2

\Qrr (T ) [^0 I

л) V T л

np H 2 O ,

где Q_VR ( T ) – колебательно-вращательная статистическая сумма, которую для нелинейных молекул можно аппроксимировать с хорошей точностью простой зависимостью ~( T / T ₀)^3/2.

Поскольку вклад в окно прозрачности дают две соседние полосы паров воды: 6,3 мкм колебательно-вращательная полоса и вращательная полоса, то для каждой полосы мы оценили средние значения энергии нижнего состояния E ₀, которые имели значения 315,04 см^–1 и 433,35 см^–1 соответственно. Для того чтобы температурная зависимость коэффициента поглощения k_f была подобной k_s , мы получили аппроксимацию в виде:

k f

с   ^Tf V T T )

= ^Cf e  ^{V    0 л} nP H ₂ O ,

где T_f = 1 100 K.

Наши оценки показали, что температурная зависимость для коэффициента k_f отрицательная, как и для k_s . На рисунке 2 приведены температурные зависимости коэффициентов k_s и k_f ..

В условиях атмосферы Земли меняются все термодинамические параметры, от которых зависит коэффициент континуального поглощения: температура, давление воздуха и влажность. Для того чтобы проанализировать поведение коэффициента континуального поглощения при различных температурах, расчет проводился при фиксированных значениях давления (1 атм) и относительной влажности (50 %).

На рисунке 3 приведен расчет коэффициента континуального поглощения по нашей модели согласно данным [6] без учета уширения воздухом (кривая В ).

Для того чтобы учесть уширение воздухом, мы ввели коэффициент у = C f- / C s , равный 0,00/ при температуре 296 К, который был выбран таким образом, чтобы при низких температурах коэффициент континуального поглощения совпадал с моделью RSB (кривая В 1), а при повышенных температурах совпадал в пределах погрешности с данными эксперимента [6]. Результаты моделирования показали, что значение коэффициента у = 0,0011 обеспечивало совпадение расчетов по нашей модели с моделью MTCKD в температурном диапазоне 250–290 К. Аналогичная картина наблюдалась и для других частот. Таким образом, две модели с различными параметрами хорошо описывают температурную зависимость коэффициента поглощения для условий, реализующихся в атмосфере Земли. Это, по нашему мнению, и объясняет противоречие между данными натурных и лабораторных измерений.

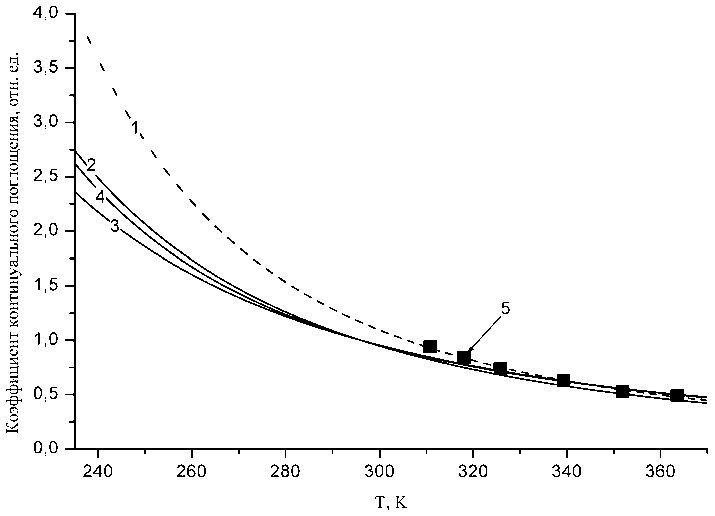
Рис. 2. Температурная зависимость коэффициентов континуального поглощения на длине волны 1 144,5 см–1:

1 – k_s ; 2 – k_f для вращательной полосы воды; 3 – k_f для 6,3 мкм полосы воды;

4 – усредненная температурная зависимость k_f ; 5 – экспериментальные данные [6]

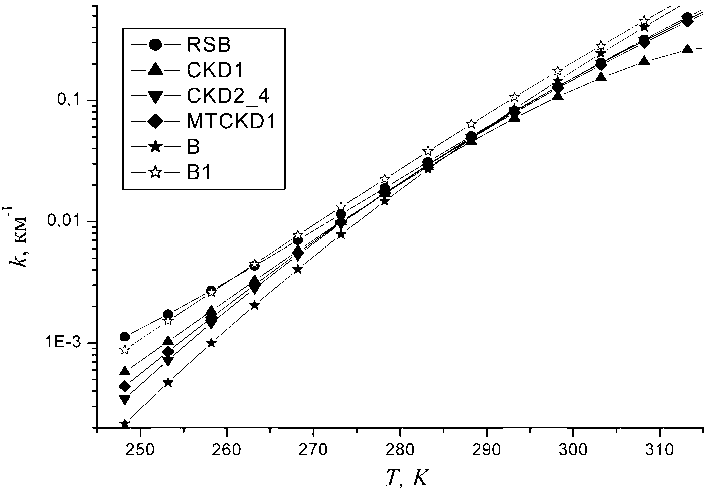
Рис. 3. Зависимость коэффициента континуального поглощения паров воды для частоты 950 см^–1 от температуры при относительной влажности 50 %. B , B 1 – расчет на основе данных работы [6] без учета и с учетом уширения воздухом

Из рисунка 3 видно, что вклад «foreign» континуума наиболее существенен при низкой температуре. Однако при температуре ниже 0 оС величина коэффициента континуального поглощения менее 0,1 км–1. Это означает, что в лабораторных условиях для уверенной регистрации необходимы трассы длиной 5–10 км и более, что на сегодняшний день проблематично реализовать. Следовательно, необходим атмосферный эксперимент в строго контролируемых атмосферных условиях. Периодически такие эксперименты проводятся (см., например: [9; 15; 17; 21]). Следу- ет заметить, что эти эксперименты в основном проводятся в полосах поглощения, а не в окне прозрачности вследствие малости коэффициентов поглощения.

Тем не менее мы провели численный эксперимент по расчету нисходящих потоков излучения с умеренным спектральным разрешением (20 см–1) для зимних условий Западной Сибири. Результаты моделирования представлены на рисунке 4.

Из рисунка 4 видно, что регрессионные зависимости для двух моделей заметно различаются (~20 %). Основная причина этого расхождения обусловлена различиями в значениях параметра γ (см. табл. 1).

F Rt/m²             940-960 см ¹          • RSB

V                                      о MTCKD1

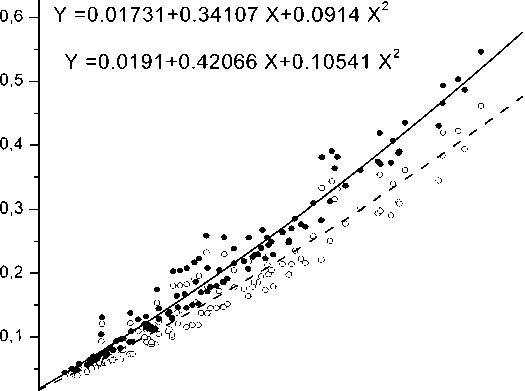
0,0

0,0         0,2         0,4         0,6         0,8         1,0         1,2

Рис. 4. Регрессионная зависимость нисходящего потока излучения на уровне Земли от общего влагосодержания в вертикальном столбе атмосферы

Следовательно, можно ставить вопрос о проведении атмосферного эксперимента по упрощенной схеме: одновременно с измерениями нисходящих потоков излучения определять общее содержание паров воды в вертикальном столбе атмосферы. А если помимо этого учесть вертикальные профили температуры, то из анализа полученной статистической информации можно будет уточнить коэффициенты континуального поглощения, обусловленные уширением воздуха k_f и уменьшить существующие неопределенности.