Самодействие электромагнитного заряда в кротовой норе с бесконечно короткой горловиной

Покоящаяся заряженная частица, в искривленном пространстве-времени порождает поле, которое из-за. кривизны пространства-времени и нелокальной структуры безмассового поля воздействует па. саму частицу. Такая сила, называется силой самодействия [1]. Аналогичная ситуация имеет место и в случае гравитационного заряда. [2-4]. Электромагнитные и гравитационные силы самодействия важны при описании движения двух тел с экстремальным соотношением масс этих тел и при исследовании излучаемых ими гравитационных воли [5,6]. В искривленных пространствах интенсивные исследования эффекта, самодействия покоящегося заряда, проводились па. фоне черных дыр, пространств топологических дефектов и кротовых пор.

В случаях статического заряда, в пространстве Шварцшильда, электростатический потенциал и электромагнитная сила, самодействия известны в явном виде [7-10]. В черной дыре Рейснера-Нордстрёма. электростатический потенциал был получен в [ИД2], а. в пространстве-времени Керра. в работах [13,14]. Сила, самодействия покоящегося скалярного заряда, в черной дыре Керра-Ньюмапа была, расмотрепа в [15].

• * Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-02-00496.

Для понимания эффекта, самодействия интересны работы в пространствах топологических дефектов (например, бесконечно длинная прямая космическая струпа, глобальный монополь), поскольку этот эффект чувствителен не только к искривлённости пространства-времени, по и к его топологической структуре [16-19].

Пространства, кротовых пор также интересны при изучении эффекта, самодействия, поскольку имеют и нетривиальную топологическую структуру и кривизну. Для статического скалярного и электромагнитного заряда, эффект самодействия в пространстве-времени кротовых нор с различными формами горловины был рассмотрен в работах [20-22]. Интересно отметить, что в длинной горловине эффект самодействия является локальным даже для безмассового скалярного поля неминимально связанного с кривизной пространства-времени [23].

Целью настоящей статьи является анализ эффекта, самодействия заряда, в пространстве-времени кротовой поры с бесконечно короткой горловиной. Предполагается, что заряд является источником электромагнитного поля, неминимально связанного с кривизной пространства-времени. Статья организована, следующим образом. В разделе II мы получаем пеперепормироваппое выражение для потенциала, самодействия статического электромагнитного заряда, на. рассматриваемом гравитационном фоне. В разделе III описывается процедура, перенормировки потенциала, самодей-ствия и результат.

В этой работе мы используем следующие определения тензора кривизны К двс = д е Г дв — д в Г де +Г ус Г^дд — Г^д_в Г де ^и тензор а Римана R mn = R mfn- Система единиц выбрана так, что с = G = 1.

1. Сила самодействия

Рассмотрим статическую сферически симметричную кротовую пору ds2 = — dt2 + dr2 + L(r)2 (d62 + sin2 6dp2) ,

где —то < r <  то, 6 G [0, тг], p G [0, 2тг).

Простейшей моделью кротовой поры является модель с бесконечно короткой горловиной

L(r) = (|r| + а), й > 0, которую мы и будем рассматривать в дальнейшем. Такая модель представляет собой два. пространства-времени Минковского, в каждом из которых вырезай шар радиуса а, и склеенных по поверхности этих шаров. Как известно, такая модель хорошо работает при описании эффектов на. больших (по сравнению с длиной и радиусом горловины) расстояниях от горловины кротовой поры.

Уравнения поля, создаваемого электромагнитным зарядом, может быть получено варьированием по потенциалу электромагнитного поля соответствующего действия. Мы рассмотрим теорию гравитации Эйнштейна, с линейной по кривизне связью между электромагнитным и гравитационным полями, для которой действие имеет вид [24]

s = у d⁴xV—g £ = 16г / d⁴$V—g (R — FmnF^mn + х^гктп^ тп ) ,          (з)

где g - детерминант метрического тензора g^, R-скалярная кривизна пространства-времени, величина.

гктп — Q1R im кп in кт 42/ nim кп от кт кп гт nhn in     гктп x = 2z g —g g )+t(R g —R g +R g —R g )+q3R называется тензором восприимчивости,

F iк = ^ г А к — ^ к А г = к — дх^г

дА г дх^к’

есть тензор электромагнитного поля, Я^гп - тензор Риччи, Д^гктп - тензор кривизны и q1, q₂, q 3 произвольные параметры теории.

Вариация по потенциалу А ^ действия (3) приводит к уравнениям электромагнитного поля

V ; Н^гк = 0 ,

где Н^гк - тензор индукции, определяемый выражением

Нгк

= р^гк

^ кти. р

Если поле А_г(ж^к ) создаётся зарядом е, то уравнения (6) преобразуются к виду

VkНгk =

-4^у'г =

—4^е

У Мг(т)5⁽4) (х^к ,Х^к(т ))

dT

, V-д

где и^г - 4-скорость заряда и т - его собственное время. Мировая линия заряда задается функциями х^к(т ). Для заряда в состоянии покоя 4-скорость заряда имеет координаты и^г(1, 0, 0, 0), а векторный потенциал A_г не зависит от времени, что позволяет использовать следующий анзац: A_г = (A_t, 0, 0, 0). Калибровка Лоренца в этом случае тождественно выполняется и система уравнений (8) сводится к одному уравнению на A_t:

8 5(т)         4 5(т)      d?At        2sgn(т)    / 8 5'(т) _    + (|т| + а) q1 1 (|т| + а) q \ dr2 1 [ (|т| + а) 1 \(|т| + а) 16sgn(T)5(r)\       / 45'(т)     4sgn(T)5(r)\     dAt            1 + (|т| + а)2 ) q1 1 \(|т| + а) 1    (|т| + а)2 / q2] dr 1 [ (|т| + а)2 85(т)           25(т)       d2At cos(6)          1           85(т) + (|т| + а)3 q1  ' (|т| + а)3 q2\  d62   ' sin(6)  [ (|т| + а)2  ' (|т| + а)3 q1 25 (т)     1 dAt       1 Г       1           85 (т) + (|т| + а)3 q2J d6 ' sin2(6) [ (|т| + а)2 ' (|т| + а)3 q1 25(т)     1 d2At      4^е53(т, 6,ф; т, 0, ф?) (|т| + а)3 q2\ d^2           (|т| + а)2 sin(6) ’                                                   ^' * где штрихом обозначена производная по т. Поскольку рассматриваемая задача сферически симметрична, потенциал удобно разложить по угловым гармоникам

∞

^AtO, Ж) = 1^^ ^тХФф^т^'лЫ^? = ' ^ ^{(21 + 1)}^i^(cos7Хдф^г),      (10)

1,т                                      1 =0

где Y_im(6, ф) сферические функции. P i - миогочлс!i Лежандра, cos 7 = cos 6 cos 6 + sin 6 sin 6 cos(^ — ф). В силу свойств сферических функций, радиальная часть, g i (т; т), удовлетворяет уравнению

Г . ₊ 8 5(т)    ₊ 4 5(т)    1 d? g i (т, Т) + Г- 2sgn(т) + / 8 5’(т)

(|т| + a) ^q 1    (|т| + a) ^q2       dr²             (|т| + а)       (|т| + а)

16 в§Л1(т)5(т)             4 5'(т)     4sgn(т)5(т)        dgi (т, т)

⁺ (|т| + а)²   у ^q 1 ⁺ \(|т| +а)⁺ (|т| + а)²  / ^q2 dт

¹         ,     85^(т)        _     25^(т)

^{—l(l + 1) —} (Яж           ^q1            ^q 2 ^gi(T,T)

5(т; Т)

(П)

(|т| + а)2

Решение этого уравнения представим в следующем виде gi (т; Т) = 6(т — T)p„i(т^щ(Т) + 6(Т — т)рп1(гфщ(т), где моды рп1(г) и ’п1 (г) удовлетворяют соответствующим однородным уравнениям

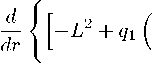
-² + ^2L' ² + 4^LL") +2q₂LL-’ ] {

[ 1 , ^4L’’    , ^L" if Р п1 ^(г) 1 _n

^{1(1 + 1)} [^{-1 +       +} Т’²] | ,„,(,) J’⁰-

рп1(г) выбирается как решение, стремящееся к нулю при г ^ +то и расходящееся при г ^ —то, а ’п1(г) выбирается как решение, стремящееся к нулю при г ^ —то и расходящееся при г ^ +то, то есть lim р„1(г) = 0, lim qni(г) = то,

Г/ + М            Г/ + М lim рп(г) = то, lim ’п(г) = 0.

г / — м              г / — м

Нормализации д [ (т; г) достигается путём интегрирования (11) по г от г — е до г + е при е ^ 0. Это приводит к условию па. Вронскиан

Г    А’ п1 -     Арп i ~l =      1

[Р”¹ Аг     ’^п1 Аг \     (|г| + о)²

Обозначим область г >  0 как Р₊, а область г <  0 как Р_—. В плоских областях Р₊ и Р_—, где L(г) = ±г + о, L‘(г) = ±1, Я(г) = 0, уравнение(13) принимает вид

( _А2

( Аг2

2 А г ± о Аг

1(1 +1)

(г ± о)2

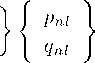
= 0.

Независимые решения этих уравнений легко получить ф±(г) = (о ± г)1, ф±(г) = (о ± г) 1 1, для/ > 0.(17)

Асимптотики этих решений при / > 0 обладают следующими свойствами ф1 |г--/ ' М ( то, ф1 Ь--/ М ( то, ф2 Ь /+м   ^ 0,   Ф2 |г / — м^

Общие решения уравнений (16) являются линейными комбинациями независимых решений (17)

Рп1(г) = а+ф+ офф— + ^+ф+, + ФХФ2, г > 0 г < 0 , ’п1(г) = ( а+ф+ 02 ф— + ф2+ф+, + З2 ф2 , г > 0 г < 0 , (19) где а±2 и ^±2 константы. Подставляя выражения (19) в (14) и учитывая (17), получим а+ = 0, о2 = 0.(20)

Тогда, решения (19) сводятся к следующему виду

Рп1(г)	=	ф+ф+, о^ф— + з—ф 2 ,	г > 0 г < 0 ,
’п1(г)	(	о+ф+ +ф2+ф+, З 2 ф2 ,	г > 0 г < 0 ,	(21)

Подставляя эти выражения в (15), получим

(|т| + а)2

“2⁺3+ ф+t ^ - Ф+ ^ , т> 0; /                                    /

-В-  - N-__r йФ-^

“1 ³² ^1 йт    ^Ф2 dr ) ’ ^т < ^0.

С учётом (17) эти выражения можно переписать в виде

(|т| + а)2

“+3+

“- ³-

( 2Z + 1 \ (т + а)²

( 2Z + 1 \ (а — т)²

т >  0;

т <  0.

Таким образом, мы получили следующие ограничения на “±₂ и 3±₂

“⁺³⁺ = “1³2 = _2Z + ,

Чтобы найти решение во всем пространстве-времени, мы должны сшить решения p_H i и q_H i и их производные по т на горловине кротовой поры т = 0. Первое условие даёт

Ртг1( — 0) = Рп.1 (+0), Qnl( — 0) = Чп1 (+0).(25)

Это означает

(“^-0^- + 3-Ф-З   _п = 3 + Ф + \ _п,

2 р 0       12 р 0

(“+Ф+ + 3+Ф+) |р—0 = 3—Ф— |р—-0 ,(26)

или

“-а¹ + 3- _ai+_T =  3i⁺_ai+_T ,

“+а1 + 3+ ^ = 3- а1+Т.(27)

Наличие 5-образного источника на горловине приводит к разрыву первых производных p„i и q_H i на величину, которую можно определить, интегрируя уравнение (13) в интервале (—е, е), а затем, переходя к переделу е ^ 0. Это даёт

dpTt i йт dq ^i йт	г—-0 г—-0	=   dp„i йт = dq ^i йт	+—3Z(Z + 1)(4q1 + q2)pni(+0), р—+0   а3 +—3Z(Z + 1)(4q1+ q2)qni(+0). р—+0   а3	(28)
Используя (21) получим	dp „i йт	р—-0	—“-Zаl-1 + 3-(Z + 1)а-l-2,
	dp ni йт dq ^i йт	р—+0 р—-0	—3+(Z + 1)а-l-2, 3-(Z + 1)а-l-2,
	dq ^i йт	р—+0	“+Zаl-1 — 3+(Z + 1)а-l-2.	(29)
и, наконец, вставляя эти соотношения в (28), получим

Находя а- , а 2, 3- , 3- from (27, 30) и подставляя их в первое из выражений (24), получаем й21+1 (й2 - 2Z(Z + 1)(4qx + 92)) 3+3+ =--------z------------4                      (31)

2(2Z + 1)(Z + 1) ^й² — Z(4qx + 92) J

Если г > г > 0, тогда из (12, 21, 17, 24, 31) получаем бДг, г) в следующем виде

9 1 (г,г) = а + 3 1 + ^+(г>+(г)+ 3+3+ ^⁺(г>⁺(г) = ^у^й + г)^-1-1 (й + Г)¹

й^{2 1 +1} / й² — 2Z(Z + 1)(4qi + 92))

-- ---------₇----------------(й + г) ^{- 1 - 1}(й + г)^-1-1                  (32) 2(2Z + 1)(Z + 1) ( й² — Z(491 + 92))

Тогда, потенциал (10) можно записать в виде

∞∞ й + г\'   ,

) Pl (cosy) \ й + г

A_t(x,X) = —е Е (2Z + 1) P i (cosy )_9l (г,г) = — ^^т Е l=0                                        ^г l =0

е ~           й^{2 1 +1} ( й^{2 — 2Z(Z + 1)(4}91 ⁺ 92))

⁺ уЕ^{р (cosy} -----—7-------------\ ^У|" ^{+ г)     (й + г)        (33)}

• ² 1=0              (Z + 1) (й² — Z(491 + 92))

Первый член правой части этого выражения можно легко вычислить, используя

∞

V1 — 2xt + t² ,

Е ^(х) = l=0

что даёт

A “ (x,X)

е й + г

^     ~

Е (~I-) pl(cosy) =

\ й + г l=0

е

(й + г)² — 2(й + г)(й + г) cos(y) + (й + г)²

Это выражение расходится при г ^ г и должно быть, как известно, перенормировано.

• 2.    Перенормировка и результат

Процедура, определения силы самодействия требует перенормировки векторного потенциала. A ^ (х; X), который расходится в переделе х ^ Т (см., например, работы [25,26]). Перенормировка векторного потенциала A_t(x;X), регуляризованного раздвижкой точек, достигается вычитанием из A_t(x;X) контрчлена Девитта-Швингера A_Ds(x;X), а затем вычислением предела х ^ х

Аге„(х) = lim (At(x;X) — ADs(x; X)). 5^^

Для покоящегося скалярного заряда, в статическом искривленном пространстве-времени кои-трчлен Девитта-Швингера ADs(x;X) имеет следующий вид [27]

А (х^г-е(— + ^d9tt(X) ____^^(37)

Ad ДХ   ) е V2^ + ^ 4gtt(X)V2^ ’                      *  ’ где (см. [28,29])

ст^г = — (х^г — X⁴) — |rj_fe (x^J' — X^j ) (x^fe — X^fe)

• — 6 (^г)_т^гы + ^Ц^) (x^J — ^XJ) (X^fc — ^X ) (x^l — ^Xl) + О ((X — ^X)⁴) ,

a = " ./■ ,                                                                           (38)

Г^_к -символы Кристоффеля, вычисленные в точке ж. Контрчлен Девитта-Швингера A_{D s}(t; 5) в пределе t = t, 6 = 6, ф = ф можно легко вычислить в пространстве-времени с метрикой (1)

е

AД; г) =  ---- (39)

| г — г |

Таким образом, мы получаем выражение для перенормированного потенциала в области г > 0

АД (г)

lim (A_t(г, г ) — A_{d 5}(г, г))

Т ^ Т

∞ е у

1=0

Д+ЧЛ ^— 2l⁽l + 1⁾⁽4qx + Д) ------------7 --------------------^{(й + г) 1} .

^(l + 1) ( й^{2 — l(} 4 q i + 9 2))

Aren в области г < 0 совпадает с этим выражением в силу симметрии задачи. Потенциал самодей- ствия и тетрадная компонента, силы самодействия имеют вид р (т)

dU self дг

U self = - ^еА^геп

2 t

~ й²¹⁺¹ (й^{2 — 2l(l + 1})⁽⁴q i + q₂))

Е-----ЛX-----"(й + г) ^{- 2 1 - 3}. i =о        62 — l(4qi + 92))

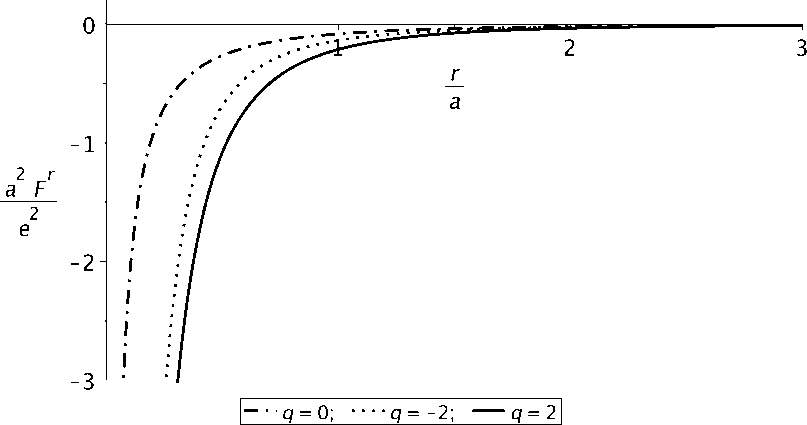
Рис. 1. График F (’’) для различиых значений q = 4 ^ 1 ++ ^ ² vs ^.

Заключение

Расходимость F ^{( т )} в окрестиости г = 0 связана с недостатком рассмотренной модели кротовой норы (модель с бесконечно короткой горловиной). В этой области её использование некорректно. Многочисленные описания эффекта, самодействия в кротовых норах с гладкой горловиной показывают, что подобной расходимости в таких кротовых порах не возникает.

В частном случае 4q 1 + q₂ = 0 результат (42) совпадает с рассмотренным ранее в работе [30].

Исследование выполнено при финансовой поддержке РФФИ в рамках научного проекта № 19-02-004 96. Работа выполнена также за счёт средств субсидии, выделенной в рамках государ- ственной поддержки Казанского (Приволжского) федерального университета в целят повышения его конкурентоспособности среди ведущих мировых научно-образовательных центров.