Самостоятельная работа - фактор качества образования

К проблеме самостоятельной работы мы уже обращались ранее. В частности, нами был представлен материал о влиянии самостоятельной работы на качество образования, сопровождающийся математической моделью этого влияния. Необходимые данные были получены в ходе первого этапа эксперимента, проведенного со студентами I курса экономического факультета Чувашской государственной сельскохозяйственной академии по дисциплине «Информатика» [3].

В помощь студентам при выполнении ими самостоятельной работы были разработаны методические пособия [2; 5], составленные с учетом требований полноты учебного материала, его целостности, логической последовательности, степени сложности в процессе изучения, а также рекомендаций ведущих ученых [1; 2; 4; 6—8]. При этом предполагалось, что каждое задание должно быть выполнено с применением компьютерной техники.

Полученные на первом этапе эксперимента результаты позволили увидеть существенную разницу в изменении уровня успеваемости студентов экспериментальной и контрольной групп, а также обнаружить «эффект адаптации», являющийся следствием различий процессов обучения в средней и высшей школе и резкого увеличения объема информации в вузе.

На основе экспериментальных данных завершающего этапа нами были построены математические модели успеваемости студентов экспериментальной и контрольной групп. Опустив сложные расчеты, ниже мы приводим геометрическую интерпретацию данных моделей.

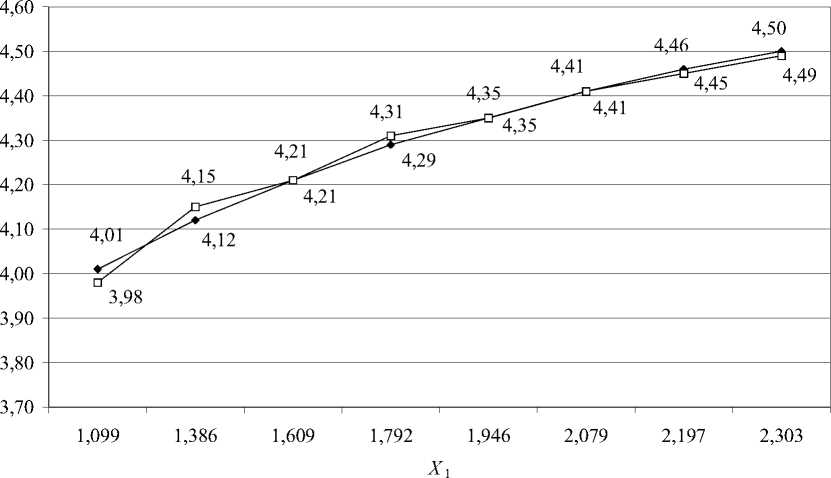
В математической модели развития результатов самостоятельной работы студентов был использован тренд Y = = 0,41 ln x + 3,55. Как свидетельствует графическая иллюстрация математической модели экспериментальной группы (рис. 1), данная модель объективна.

Качество модели подтверждается коэффициентом линейной корреляции r = 0,995 и коэффициентом детерминации R² = 0,9906, означающим, что выбранная структура тренда учитывает 99,06 % факторов, влияющих на результаты самостоятельной работы, а неучтенные факторы составляют лишь 0,94 %.

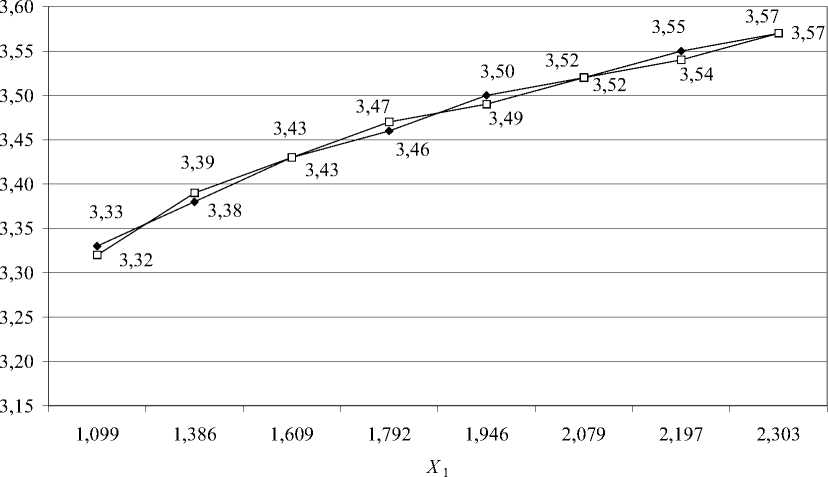
Ниже представлены аналогичная математическая модель для контрольной группы (структура тренда Y = = 0,19 ln x + 3,10) и ее графическая иллюстрация (рис. 2).

Как показывают параметры качества данной модели (r xy = 0,998 и R² = 0,965), в этом случае доля неучтенных факторов составляет 3,5 %.

^ 3^^ ^ЙЙЙЙЙЙЙЙ^^ ИНТЕГРАЦИЯ ОБРАЗОВАНИЯ jWWWSSS^®

Средний балл                                                    Средний балл

Yx Y1

Р и с. 1. Математическая модель успеваемости экспериментальной группы:

Y1 — исходные данные по самостоятельной работе; Yx — построенная математическая модель

Yx Y1

Р и с. 2. Математическая модель успеваемости контрольной группы:

Y1 — исходные данные по промежуточной аттестации; Yx — построенная математическая модель

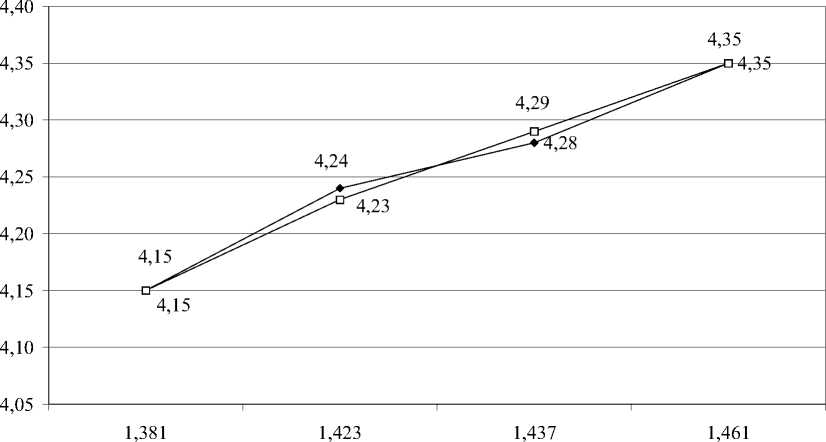
Построенная на первом этапе математическая модель зависимости качества образования от самостоятельной работы со структурой тренда Y = 2,36 ln x + 0,88 (рис. 3) была подвергнута сравнению с фактическими результатами успеваемости студентов.

Процедура сравнения выявила отличие результата прогнозируемого показателя математической модели от фактического на 0,02 балла, что является подтверждением параметров качества предлагаемой модели (г = 0,981, R² = = 0,963). xy

X 1

Yx Y1

Р и с. 3. Математическая модель влияния самостоятельной работы на успеваемость студентов на начальном этапе:

Y1 — исходные данные промежуточной аттестации;

Yx — построенная математическая модель

На завершающем этапе была проверена математическая модель зависимости успеваемости студентов от результатов самостоятельной работы путем следующего алгоритма.

• 1.    На основании результатов некоторого количества самостоятельных работ строится математическая модель и определяется прогноз результата успеваемости на следующем этапе.

• 2.    Сделанный прогноз сопоставляется с фактическим результатом успеваемости, полученным после проведения очередной самостоятельной работы. Эта процедура повторяется до завершения эксперимента.

Проведенный сравнительный анализ фактических результатов успеваемости и прогноза по построенной математической модели влияния самостоятельной работы на показатель успеваемости позволяет сделать следующие выводы:

• 1)    бесспорно, самостоятельная работа влияет на показатель успеваемости студентов (в экспериментальной группе показатель успеваемости на 25,77 % выше, чем в контрольной);

• 2)    построенные математические модели объективно отражают результаты эксперимента и представляют интерес при получении прогнозов в подобных исследованиях.

^ 3^^ iSSSSSSSSSSSS ИНТЕГРАЦИЯ ОБРАЗОВАНИЯ jWWWSSS^® 4,60 4,50 4,40 S 4,30 5 4,20 4,10 4,00 3,90

Yx Y1

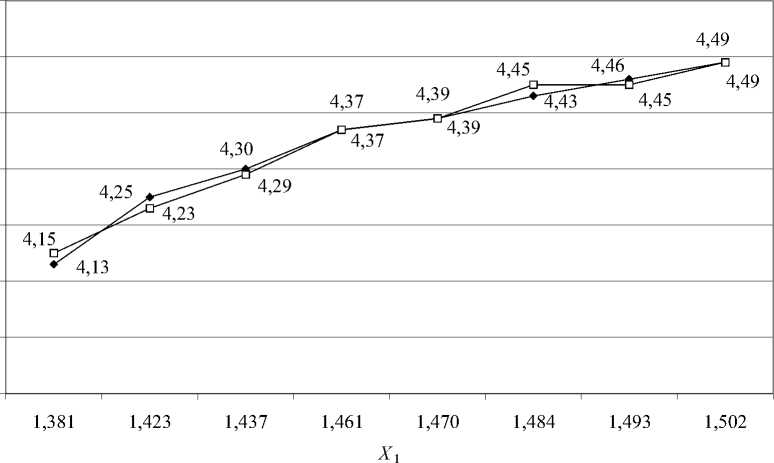
Р и с. 4. Математическая модель влияния самостоятельной работы на успеваемость студентов на завершающем этапе:

Y1 — исходные данные промежуточной аттестации;

Yx — построенная математическая модель

На рис. 4 дана графическая интерпретация модели и фактических результатов (структура тренда Y = 2,92 ln x + + 0,09). Качество модели подтверждается коэффициентом линейной корреляции r xy = 0,992 и коэффициентом детерминации R² = 0,9859, означающим, что выбранная структура тренда учитывает 98,59 % факторов, влияющих на результаты самостоятельной работы студентов, а неучтенные факторы составляют лишь 1,41 %.

Судя по результатам проведенного эксперимента и расчетам по построенным математическим моделям, наблюдается повышение успеваемости студентов с 24,02 % на первом этапе до 25,77 % на завершающем этапе эксперимента.

Таким образом, из представленных расчетов следуют актуальность и значимость проблемы самостоятельной работы студентов. Такая работа способствует достижению цели учебного процесса и повышению качества знаний студентов.