Сценарии осцилляций и гибели в новой непрерывной модели эруптивной фазы инвазии чужеродного вида
Автор: Переварюха Андрей Юрьевич
Журнал: Математическая физика и компьютерное моделирование @mpcm-jvolsu
Рубрика: Моделирование, информатика и управление
Статья в выпуске: 1 т.22, 2019 года.
Бесплатный доступ
Рассматривается проблема моделирования развития особых популяционных процессов, которые включают прохождение эруптивной фазы динамики. Подобные непродолжительные, но ураганные режимы часто связаны с последствиями инвазий нежелательных биологических видов. Процессы при вселении вида часто могут развиваться через отложенную во времени фазу стремительного увеличения его численности. Завершение фазы зависит от многих факторов. Вспышки отдельных биологических видов оказывают столь сильное давление на среду, что достижение ненулевого балансового равновесия проблематично. Подобные явления трактуются нами как переходный процесс с эруптивной фазой к неопределенному заранее состоянию биотической среды. В зависимости от противодействия, что ярко видно на примерах динамики насекомых-вредителей, сценарии подобных явлений могут развиваться различным образом, в том числе с разрушением среды обитания. Разработана новая модель на основе уравнения с отклоняющимся аргументом, где описан вариант развития повторной вспышки катастрофического характера. Сценарий реализуется при возникновении негармонического цикла 𝑁*(𝑟, 𝑡), который при специфических условиях не может быть орбитально устойчивым, но становится переходным. Цикл завершается тривиальным значением. Моделируемый сценарий наиболее резкой формы эруптивной фазы заканчивается в вычислительном эксперименте полной гибелью инвазионной популяции, но без образования неограниченной сверху траектории из колебаний. Гибель происходит при разрушении релаксационного цикла экстремальной амплитуды в рассмотренном нами уравнении популяционной вспышки в предыдущей нашей работе [2].
Уравнения с запаздыванием, чужеродные виды, колебания популяций, переходные режимы, моделирование биологических инвазионных явлений, эруптивная фаза вспышки
Короткий адрес: https://sciup.org/149129854
IDR: 149129854 | УДК: 57.02.001.57, | DOI: 10.15688/mpcm.jvolsu.2019.1.5
Текст научной статьи Сценарии осцилляций и гибели в новой непрерывной модели эруптивной фазы инвазии чужеродного вида
DOI:
В предыдущей работе [2] мы рассмотрели модель специфического сценария развития популяционного процесса при существенном влиянии запаздывающей регуляции и наличии некоторого уровня 2 опасного насыщения: 2 < К . Мы предложили иную трактовку значения порога численности вместо традиционной К — предельной, плавно достигаемой «емкости ниши». В нашей модели сценарий приближения N (t) ^ 2 означает не уравновешивание системы в ситуации новый вид — среда, но достаточно жесткий уровень угрозы среде.
Переход через значимый уровень численности имеет последствия для скрытых от наблюдателя механизмов контроля эффективности воспроизводства. Фиксированная величина репродуктивного потенциала г — понятие абстрактное и математическое, его изменения — сложный вопрос. Для популяции насекомых есть величина средней плодовитости и коэффициенты дожития по стадиям развития. На размножение насекомых (как и многих других животных) оказывают влияние случайные факторы — стохастичность колебаний среды. Чем меньше группа особей, тем сильнее влияние возмущений. Если существует значение численности 2, при котором случайные негативные факторы уже не значимы, то на динамику системы оказывает влияние отклонение 5 = (2 — N(t — т)). Величина отклонения δ может быть как положительной, так и отрицательной. Запаздывание τ в модель мы включили в оба сомножителя, получив следующее уравнение на базе модели Хатчинсона:
N = rN (1 — ) (2 — N (t — т)). (1) at у К /
Можно считать, что при смене знака δ члены правой части (воспроизводства и регуляции) меняются своими функциональными ролями в модели, то есть успех воспроизводства станет пропорционален AN 2 , 5 < 0. Модель позволила описать специфическую деградацию вида в нестабильной среде обитания. При увеличении значения U = гт в (1) возникнет устойчивый цикл N * (г т , t) — общее свойство таких уравнений с запаздыванием t — т. При чуть большем увеличении U = гт + 5 Г произойдет резкое изменение поведения уравнения. Траектория перестанет притягиваться к замкнутому подмножеству фазового пространства, обозначаемому обычно N * ( U ,t) — c указанием управляющего параметра.
После бифуркации траектория (1) вместо установления из переходного режима цикла с все увеличивающейся (приемлемой только для одноклеточных организмов) амплитудой может быть резко выброшена за пределы допустимых для существования вида значений при N(t — т) > К . Такая потеря установившегося режима считается катастрофической. Реализуется сценарий разрушения возникшего при бифуркации цикла с образованием недиссипативной траектории — maxN * ( U ,t) в релаксационных колебаниях преодолевает значение емкости К , и далее N (t) ^ то , но с псевдопериодической компонентой (подобной функции e f sin(y(t))) как в вычислительном эксперименте (рис. 1).
Очевидный пример описанной ситуации — кризис островной биосистемы. Размножившиеся олени, завезенные на остров Врангеля в XIX в., вытоптали лишайниковые пастбища. Ситуация повторилась в точности с быстрым крахом интродуцированной популяции оленей Rangifer tarandus на острове святого Матфея [11] в 1963 году Охота на оленей прекратилась, а факторы внутренней регуляции проявили запаздывание [14].
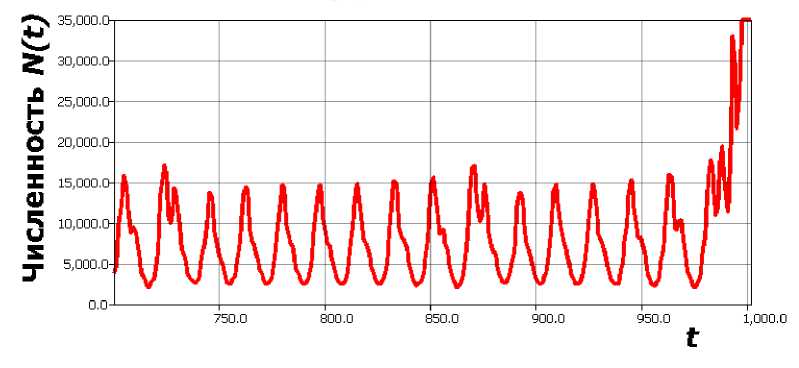
Рис. 1. Разрушение цикла в катастрофическом сценарии модели (1) S = 5 000 , К = 15 000
Для некоторых популяций леммингов после серии флуктуаций с выраженным пиком численности в конце периода цикла свойственно наступление периода депрессии — без выраженных колебаний. Мелкие грызуны оказывают значительное воздействие на хрупкую арктическую экосистему при пиках своей активности [8]. В реальности циклы их популяции со значительной амплитудой оказываются неустойчивыми. Действие возмущений, обычно климатических аспектов, переводят популяционные колебания в состояние критически низкой численности (см. рис. 2).
Мы рассматриваем случаи серьезного давления вновь образующейся популяции после вторжения (или инфекции в частном случае инвазий) на среду. Критический недостаток ресурсной базы в реальности наступает при некоторой конечной численности М ,К > М (в нашей трактовке параметра К ) еще до полного разрушения среды. Типичный пример — течение ВИЧ-инфекции с пороговым переходом в терминальную стадию. В проблеме распространения вредных насекомых в настоящее время наблюдается подобный сценарий на побережье Краснодарского края: после проникновения в 2012 г. самшитовой огневки Cydalima perspectalis происходит гибель самшитовых рощ — островков медленно растущего реликтового растения. Только начались исследования по поиску в родном ареале бабочки подходящих для биологического подавления вселенца естественных врагов [27].
Полученный сценарий в модели реалистичен, но достаточно специфичен, кризис цикла не может претендовать на обобщение взрывообразных случаев поведения вторгшихся организмов. Если первые фазы подобных процессов обладают значимыми признаками сходства у многих активно размножающихся видов, то завершение экстремальной динамики весьма разнообразно по формам графиков.
1. Актуальность экстремальных модификаций моделей математической биологии
С древнейших времен известно, что скопления насекомых-вредителей отличаются разнообразной динамикой. Отдельно выделяются сценарии разрушительных популяционных вспышек. Явление вспышек разделяется по фазам развития, но фиксируется наблюдателями в момент третьей фазы, так называемой «эруптивной» фазы — неудержимого размножения. Термин «эруптивный» используется в вулканологии, физике звезд и лесной энтомологии. Инвазии чужеродных видов могут происходить различным образом,
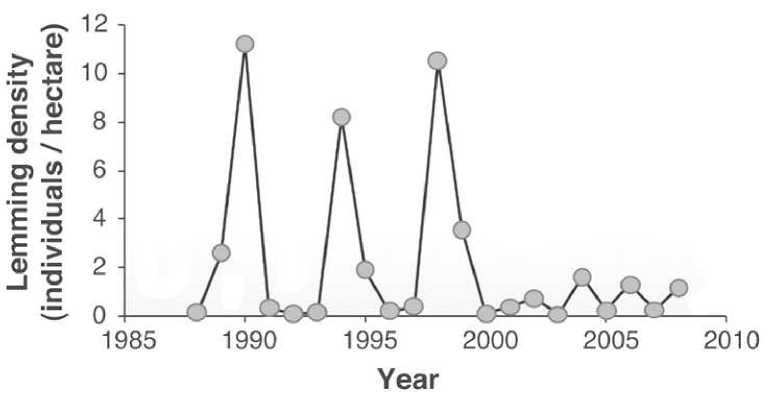
Рис. 2. Завершение популяционных циклов леммингов [8]
в том числе по негативному для вселенца сценарию с его дальнейшим исчезновением.
При моделировании мы полагаем вспышки — затухающие переходные процессы и события, которые относим к «экстремальной динамике» — явления значительные, но не повседневные. Вспышку вредителей обычно представляют в виде краткого Λ-образного пика, как описано в популярной книге Одума [16]. Из этой книги черпают представление о фундаментальных принципах экологии. Пороговый вариант запуска эруптивной фазы из стохастических колебаний описан там по данным из особых условий, а именно на примере размножения псиллид — листоблошки монофага, вредителей эвкалипта, семейство Psyllidae, вид Cardiaspina albitextura в вечнозеленом эвкалиптовом лесу. Регулятор активности псиллид — осы-паразиты 2-го порядка, что является специфическим трехзвенным взаимодействием видов разных семейств.
2. Существующие методы описания нестационарных популяционных режимов
В биологии известно много моделей межвидового взаимодействия, генерирующих колебания гармонические, релаксационные или даже апериодические. Известен «Шиль-никовский хаос» в модификациях системы уравнений Розенцвейга — МакАртура, как в работе [6]. Промежуточные состояния в экологии популяции не походят на цикли-ческие/хаотические асимптотические режимы, скорее похожи на импульсные эффекты. Помимо внутренних механизмов биотических сообществ модели популяционной динамики могут учитывать важнейшие факторы, такие как глобальные климатические изменения, но так можно рассматривать долгосрочные сценарии постепенных изменений [22]. Активно обсуждается построение наиболее общей модели динамики популяции в экосистеме, как, например, феноменологическое в работе [29]. Менее развито направление моделирования специфических, экстраординарных ситуаций в популяционных процессах, к которым можно отнести моделирование протекания очаговых инфекций в популяциях [28]. Подобные задачи анализа метаморфозов рассматривались с позиций теории катастроф [13] применительно к вспышкам численности насекомых [17]. Существуют интересные примеры применения вероятностных методов. Оригинальные современные компьютерные методы моделирования пространственного распространения вспышки плодовых мушек на основе стохастических клеточных автоматов применены в работе [26] по массивам реальных данных. В [20] разработан метод точечного стохастического возмущения поведения дискретной составляющей траектории непрерывно-дискретной модели, и возмущение наблюдается только в ограниченной области численности нерестового запаса атлантической трески.
Современным компьютерным подходом моделирования популяционных изменений называется применение мультиагентных (agent-based) алгоритмов коллективного поведения агентов как вычислительных сущностей во взаимодействии со средой, в работе [21] агентную модель удалось адаптировать для Dendroctonus ponderosae жука-вредителя в Британской Колумбии. В других современных работах уделяют внимание ландшафтным особенностям ситуаций, рассмотренных в статье [15], где применен формализм клеточных автоматов. Несмотря на развитие имитационных алгоритмов, традиционные методы вычислительного моделирования на основе уравнений с непрерывным временем, по нашему мнению, далеко не исчерпали возможностей целенаправленной модификации.
По решаемым задачам математические методы популяционной биологии можно разделить на прикладные модели (оценки эксплуатации биоресурсов или роста организмов) и уравнения системных процессов в теоретической экологии (переноса энергии по уровням, развития сукцессии). Наиболее актуальная ранее задача моделирования оптимизации эксплуатации, максимизации прибыли от объекта промысла, теряет значимость после ряда коллапсов, как, например, ситуации с треской Лабрадора [19] и осетровыми рыбами Каспийского моря [18]. В современных работах концепция Maximum sustained yield, которая предполагает полное изъятие «излишков» рыбного запаса, подвергается критике из-за повышения рисков кризиса. В реальности достижение оптимального изъятия и состояние перелова связаны с возможностью резкого истощения рыбных ресурсов [7], которое не удается прогнозировать статистическими методами.
Наши работы относятся к малоизученной проблеме математического описания закономерностей резких изменений в биосистемах. В серии работ предполагается провести построение и анализ набора вычислительных сценариев для пороговых и экстремальных эффектов в некоторых фазах специфических биологических процессов. Варианты развития кратких явлений нет смысла изучать в рамках рассмотрения асимптотической динамики. Полученные в моделях результаты значимы для теории переходных популяционных процессов, однако могут помочь в качественном объяснении неожиданных случаев деградации — коллапсов промысловых биоресурсов.
В настоящей статье автор предлагает модифицированные методы моделирования критического проявления биологического запаздывания в аспекте вариативности ответа среды на агрессию. Факторы модели включают свойство медленной эволюции параметров среды.
3. Базовые формы популяционной саморегуляции
Описание действия регуляции численности и поиск методов формализации механизмов баланса — краеугольная задача в математической экологии. В современных быстро меняющихся условиях адаптации видов не менее интересны рассматриваемые нами модели явлений, связанных со стремительным сдвигом индекса выравненности биологического разнообразия или подобными резкими нарушениями равновесия.
Уравнение с запаздыванием (1) является расширением модели Хатчинсона, которая в свою очередь представляет собой осцилляционную вариацию на тему известного уравнения модели N = rF(N2) ограниченного роста sup N(t) = К популяции Ферхюль- ста [10]. Будет ли популяция на всем возможном диапазоне численности подчиняться уравнению асимптотического роста — оставалось для демографии вопросом.
Скорее из социально-экономических соображений полагалось у уравнения N = = г/ (N 2 ) наличие точки обращения в ноль производной правой части по переменной N , так что / / (N) = 0 : / / (N) < 0, N > N и снижения скорости прироста до его остановки. Это выполняется в логистической модели на уровне «насыщения среды» /(N * ) = 0, N * = К . Что представляет емкость экологической ниши в условиях стремительной инвазии — вторжения чужеродного вида, отвоевывающего свою нишу?
Мы полагаем, базовое понятие емкость среды К имеет ограниченную область применения в контексте квадратичной (степенной) зависимости регулирования, что необходимо учитывать при построении усовершенствованных моделей.
Современная запись обобщенной логистической модели (к = 1) имеет следующий вид:
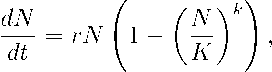
где, в модификации Ричардса, к > 1 [5]. В записи варианта Базыкина для минимально допустимой численности группы особей N = rF (N 2 ) х (N — L) и L оказывается неустойчивым равновесием [4]. Для такой критической группы нам представляется интересным из соображений о причинах возникновения экологического эффекта Allee (необходимости создавать группы особей для лучшей выживаемости потомства) объединить идеи в варианте более гибко настраиваемой модели. Ведь если виду необходимо создавать крупные скопления, значит это эволюционно целесообразно (допустимо к < 1) и компенсирует действие внутривидовой конкуренции:
1? = -(■-(К У)
(N — L),k е [1/2, 3/2],
но мы не будем рассматривать вариант (2) как принципиально новую модель вспышки активного вселенца. Далее предложим альтернативный вариант для формирующейся популяции при сопротивлении окружения.
3.1. Базовые модификации популяционной динамики с запаздыванием
Для возникающих резких режимов флуктуаций используются уравнения с запаздыванием, так как подобные колебательные режимы наблюдаются у популяций при постоянных условиях и без участия хищников, а значит нет возможности перевести ситуацию к системе уравнений с классической потерей устойчивости и бифуркацией Андронова — Хопфа. В экспериментах конкуренция за ресурсы может существовать между различными стадиями онтогенеза лабораторной популяции.
В варианте Хатчинсона, на который все опираются для построения новой модели, впервые учтена ситуация появления обобщенной запаздывающей регуляции:
£ = rN(t) (1 — ) . (3)
at у К /
При малых значениях запаздывания τ динамика модели (3) опишет затухающие колебания N (t) ^ К [10]. В (3) установлена возможность возникновения бифуркации
Андронова — Хопфа с появлением устойчивого предельного цикла N * (t,T) Нарушение критерия устойчивости состояния равновесия зависит от величины т т [1]. Дальнейшее увеличение тт > п/2 вызывает переход в режим релаксационных колебаний. Модель биологически адекватна для варианта колебаний вокруг равновесия при малой амплитуде. Быстрое увеличение амплитуды колебаний выраженной негармонической формы при малом временном промежутке между максимумами и стремящимися к нулю минимумами выводит такой релаксационный цикл за рамки допустимого экологического обоснования.
Для лучшей настройки характеристик негармонических колебаний в работе [9] предложена следующая модификация модели:
dN Л К - N(t - т) \
If = Т ( t ) ( (К + cN (t - т))) ' ()
В работе [12] она рассматривалась с приведенными коэффициентами:
dN = XN(t)J (N(t - 1)), где / — бесконечно дифференцируемая функция, разложимая в асимптотический ряд (этому условию удовлетворяет, например, /(ж) = (1 - ж)/(1 + сж)). Для (4) установлено существование единственного устойчивого релаксационного цикла неклассической формы. В такой модели коэффициент с > 0 становится еще одним параметром, определяющим характеристики цикла. При увеличении с сжимается амплитуда, хоть расстояние между минимумом и максимумом сокращается, но предельное соотношение min0 В рассмотренной автором модификации на основе (4) для узкой задачи улучшения характеристик цикла в частной проблеме моделирования пилообразной вспышки численности у бабочки-листовертки в Квебеке предложена следующая форма регуляции dN dt = TN<0 ((KK+-N2^))) - »N(t). В нашем варианте (5) очередной пик должен начинаться от некоторого значимого порога численности, это необходимо из соображений, изложенных в следующем разделе.
3.2. Противоречия дополнений /(N(t - т)) в модели инвазий В уравнениях с запаздыванием, как известно, не составляет сложности получить и анализировать вычислительными методами после бифуркации колебательные режимы сложной формы (даже апериодические). Имеется вопрос об адекватности характеристик полученных режимов при увеличении параметров для описания резких изменений. Усложнение колебаний и рост амплитуды могут сопровождаться понижением минимума цикла до е-окрестности нуля и вряд ли могут соотноситься с наблюдением за общей численностью популяции. В уравнениях Хатчинсона или модели «blowflies equation» (см. [24]) при росте амплитуды релаксационного цикла ограничением для практики являются очень малые, сколь угодно близкие к нулю минимумы колебаний, но сменяющиеся мгновенными пиками численности [12]. Предложенным нами в (5) способом удается отчасти сгладить недостаток у минимумов: min0 Вопрос о сущностной (экологическо-физиологической) природе запаздывания в регуляции дискуссионный, мы не считаем его связанным с каким-то одним интервалом времени в онтогенезе вида. Популяционные характеристики по мере прохождения фаз вспышки у насекомых могут изменяться, но данный аспект не учитывался в известных моделях вспышек.
3.3. Новая модификация уравнения состояния критического минимума При низкой плотности популяции происходят особые процессы, связанные с эффектом состояния при предельно низкой численности. Существует представление о минимально возможной низкой численности, которая допустима для существования популяции. Оговоримся, что гипотеза модели Базыкина может не выполняться для некоторых видов. Расселение сорной рыбы Perccottus glenii происходит с проникновением в водоемы единичных особей ротана. Формализовать данное представление на первый взгляд просто — добавив сомножитель N = г/(N)(N — L), но интересно это сделать другим математическим способом, чем предложил Базыкин c /(N) = (N — N2/К) [4]. Для модификации уравнения, которое станет базовым для моделирования экстремальных задач, выберем альтернативную функцию. Такая x(N) должна сохранять свойство lim/ ,^ N(t) = К, но с другим положением точки v‘(N) = 0. Запишем базовое уравнение следующим образом: ^ =г In(К)NУ<^, (6) где г — репродуктивный потенциал. В правую часть (6), где x(N) = 0, ln(N/K) = 1, добавлен сомножитель, который увеличивает число ее нулей. Подобным образом можно описать минимальную численность, связанную с эффектом Олли. Данное явление правильно представлять как триггерное (проявляющееся вдруг и резко). Снижение репродуктивного потенциала начинает наблюдаться, когда состояние популяции далеко не оптимальное. В оптимальном состоянии большой группы особей эффект никак не проявляется на регуляции численности. Выбор нами x(N) = ln(K/N) и показатель степени меньше единицы более логичен, чем для функции квадратичной регуляции /(N) = rN(1 — N/K). Установим степень 1/3 для ослаблено действующего порогового эффекта, который можно вычислительно описывать предикативно меняющей знак кусочно-постоянной функцией, но это выходит за рамки традиционной методологии. Вымирание N(t) ^ 0 в модели вида (2) будет выглядеть стремительным и безвозвратным явлением. Введение явного порога L математически наглядный, но не самый элегантный метод описания эффекта Олли. Альтернативный способ — воспользоваться стохастическим возмущением. Многие популяции могут восстанавливать численность от единичных сохранившихся особей (как бабочка-вредитель непарный шелкопряд, прочие случайные вселенцы) и через некоторое время снова демонстрировать нестационарные режимы. Наступление длительного периода депрессии или даже полное исчезновение популяций (характерно для ряда островных сообществ, где нет разреженной границы ареала) может происходить как раз не из состояния, близкого к L, но при запрещенном для (2) режиме 3t : N(t) > K,N(0) < К.
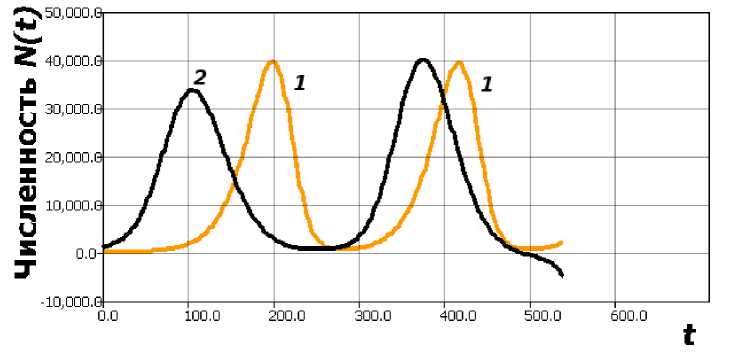
4. Модификация модели затухания предкатастрофической вспышки Практически актуальным является задача модели сценария подавления флуктуаций и перевод популяции нежелательного чужеродного вида через диапазон минимальной численности к некоторому новому незначительному стационарному уровню, не воздействующему активно на среду. Модификацию можно предложить c использованием функции v(N) = ln(K/N), но с запаздыванием: £ = гдN(t)ln () . (7) Уравнение (7) опишет актуальный для развития инвазии чужеродного вида сценарий развития единичной (почти катастрофической) вспышки численности. Взрывообразный рост при исчерпании ресурсов приходит к малочисленному состоянию. Далее траектория медленно асимптотически приходит к не воздействующему на среду балансу К. На рисунке 3 показано сравнение динамки (3) и (7) при одинаковых значениях К, т, N(0) и значении г = гд + 10. Для модели Хатчинсона тут видна отмеченная выше проблема интерпретации результатов — два резких пика при стремящихся к нулю минимумах. При полном соответствии параметров в сценарии траектория уравнения Хатчинсона N(0) < К монотонно стремится к балансу N(t) ^ К, качественно повторяя поведение модели Ферхюльста. Рис. 3. 1 — Релаксационный цикл в уравнении (3), 2 — однократная вспышка в (7), К = 15 000, т = 48, тд = 0, 017 Подобная ситуация развивалась на примере фитофага американского жука Zigo-gramma suturalis [23]. Популяция листоеда, вселенного для борьбы с сорняком амброзией, распространилась фронтом большой плотности, но далее прошла «бутылочное горло». Теперь жуки трудно обнаруживаются в естественных биотопах, иногда фиксируются единичные экземпляры. Аналогично может описываться длительное сохранение очага хронической инфекции в организме после окончания активного распространения заражения.
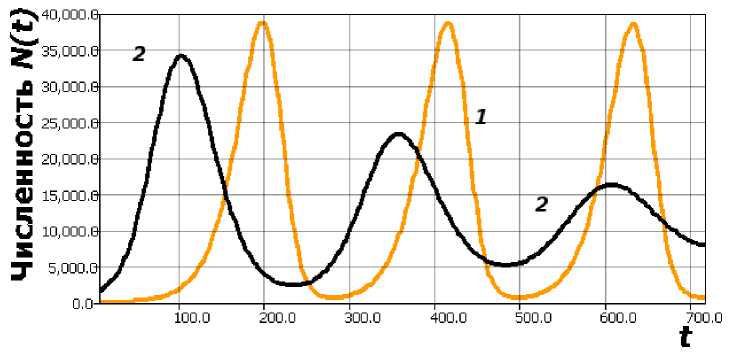
5. Модель сценария элиминации чужеродного вида При дополнении (7) сомножителем N3/(N — L): 1? =г- to (м^)N ^ N L • получим, что в (8) успешного прохождения траекторией критического минимума после максимума не наблюдается — популяция чужеродного вида после катастрофической вспышки N(t) = 0. В таких случаях говорят о неизбирательной элиминации инвазионной популяции. Подобных примеров достаточно много. В 1930–1950 гг. в Каспийское море целенаправленно акклиматизировали и вселяли многие виды рыб, но активно размножилась только черноморская кефаль в Южном Каспии. Черноморская камбала не выдержала конкуренции с тогда многочисленными популяциями осетровых. Случайный вселенец, попавший по ошибке в Нижнюю Волгу — амурский подвид карася, активно размножился, и известен рыболовам-любителям на Нижней Волге под народным названием «буфало». Результат элиминации после эруптивной фазы активного размножения можно получить и более естественным математическим средством, добавив в правую часть параметр независимой убыли —qN(t), который может отражать целенаправленное изъятие в целях борьбы с вселенцем: dN К \ . 1Г =^ln (N(t-T)) N(t) — qN(t), и эта небольшая модификация изменит качественный характер решения. В (9) после первой вспышки при инвазии идет следующая, но действительно катастрофическая, но второй глубокий минимум становится последним — вычислительный эксперимент завершается. Так как N(t) < 0 недопустимо, происходит иной вариант разрушения колебаний, чем описан в [2]. Сравнение на рисунке 4 при q = q = 0,007 тех же параметров и (II)-модификации (3) c аналогичным дополнением: dN= rN (t)A — ) — qN (t). dt \ К / Остановка расчетов, так как значения не могут быть N(t) < 0. При значении меньших порогового q < q мы получим второй пик меньше первого и увидим классические затухающие колебания. Сценарий (рис. 5) показывает эффективность включения борьбы с чужеродным видом именно в период минимумов после первой вспышки. Рис. 4. 1 — Релаксационный цикл (10), 2 — повторная катастрофическая вспышка и гибель популяции по (9), К = 15 000, т = 48, тд = 0, 017, q = 0, 007 Рис. 5. 1 — Релаксационный цикл в (10), 2 — затухающие колебания варианта (9) при К = 15 000, т = 48, Тд = 0, 017, q = 0, 006 Из новых модификаций уравнений следует экологический вывод, что после фазы эруптивной динамики инвазионный вид оказывается на некоторое время в уязвимом состоянии. Данный сценарий гораздо более благоприятен для среды, чем мы видим на прошлом нашем варианте модели (см. рис. 1). В (3) можно получить сценарий EtM, N(0) < К, т > т : N(тт,Ъм) > К, lim/ ,^ N(тт, t) = К, но подобный режим модели Хатчинсона не будет катастрофической вспышкой, но незначительным переполнением экологической ниши, и мы не увидим прохождения минимально возможных значений численности. Добавление независимой убыли в (3) улучшает свойства цикла в части смещения min N*(тт, t). Сомножитель ( \/(N — L)) действует аналогично во всех уравнениях. Формы колебаний для автохтонных и инвазионных, формирующихся в новой среде популяций, могут быть различными. Помимо затухающих и гармонических колебаний может возникать и противоположное явление — возникновение флуктуации с затяжными пиками численности. Для отдельных насекомых-вредителей, как Ostrinia nubilalis мотылек (динамика кукурузного мотылька анализировалась при участии автора в проекте РФФИ 5-04-01226 в сотрудничестве с Институтом защиты растений РАН), харак- терна ситуация с переходом к пилообразной вспышке численности в виде серии коротких пиков между длительной депрессией. В данном проекте было интересно выявление причин не экстремальной вспышки численности вредителя, но перехода к депрессии популяции. Предложенная модель (9) с запаздыванием может являться базовой для дальнейших модификаций с усложнением зависимости ln(F(N(t — т))) формы противодействия со стороны биотического окружения. Дополнения правой «репродуктивной» части запаздыванием r N(t — т) /[N(t), N(t — т)] не несут экологического смысла. Для вычислительного исследования рассматриваемых нами уравнений существуют современные производительные и проверенные библиотеки численных алгоритмов. Алгоритмы строятся на основе применения явной схемы Рунге — Кутты с плотным выводом, таким как метод Owren — Zennaro 5-го порядка [25]. Особенности применения схем Рунге — Кутты и модификация алгоритма стабилизации границ для уравнений с запаздыванием обсуждались в [3]. В настоящее время для локальных однородных уравнений вычислительные средства достаточно надежны. Заключение В развитии ранее предложенного метода мы рассмотрели две актуальные модификации модели динамики популяции для описания инвазионных процессов, способных переходить в эруптивную фазу — ограниченную во времени взрывообразную форму изменений. Сценарии учитывали, что традиционно фиксируемая в моделях емкость среды может не являться балансовым равновесием. Ситуации актуальны из обоснования, что в течение вспышки массового размножения изменяются важнейшие популяционные показатели насекомых — масса яиц и, следовательно, их жизнеспособность. Разные показатели опосредованно входят в параметрический репродуктивный потенциал. Модели феноменологически описывают варианты инвазии при разных уровнях регуляции воспроизводства чужеродного вида. Иногда адаптировавшийся инвазионный вид, как упомянутая самшитовая огневка, не встречает активного давления со стороны автохтонных видов и продолжает активно размножаться, разрушая тем среду своего обитания. Причину влияния запаздывания в регуляции мы предполагаем как обусловленную комплексом эколого-физиологических факторов. Отражаемое в F(N(t — т)) явление в такой трактовке не связано с некоторым единственным параметром, относящимся к экологии вида (как возраст созревания имаго насекомых или время миграции молоди осетровых рыб из Волги в Каспийское море). Данный аспект опаздывающей реакции служит характеристикой комплексного взаимодействия вида в конкретной среде, включая противоборствующее биотическое окружение и истощение ресурсов. Наиболее очевидна трактовка запаздывания в популяционном процессе на примере инфекции. Другая модификация предложенной модели при выраженном сопротивлении среды позволила описать именно кризис инвазионной популяции после повторной вспышки численности. В иммунологической трактовке сценария при повторной вспышке активности инвазионный объект сталкивается с популяцией прошедших отбор специфических иммунных клеток. Такие клетки уверенно связываются с антигенами. Остается актуальным дальнейшее расширение методов вычислительного моделирования замедленно активирующегося противоборства. Например, при использовании непрерывно-дискретной структуры модели для задачи математического описания частно- го, но весьма показательного сценария популяционной динамики возникновения затухающих флуктуаций. Отличие от рассмотренного нами сценария в том, что после вспышки колебания наблюдаются не вокруг равновесия lim/ ,^ N*(t) = К, но Л-образные и с фиксированным минимумом: lim/ ,^ N*(t) = minN*(t) = L интервала промежуточной депрессии численности. Взрывообразные изменения численности, разделенные на фазы, — это переходные режимы существования биосистем, поэтому вспышки не имеет смысла рассматривать в терминах аттракторов, ш-предельных множеств и асимптотической динамики траекторий. Один и тот же вид-вселенец в разных новых экосистемах показывает различную динамику. Противоположно, бесконечно далекие на эволюционном древе виды (как гребневик Mnemiopsis leidyi, проникший в Каспийское море у берегов Ирана и каспийская тюлька, вселившаяся в Рыбинском водохранилище), демонстрируют поразительное для биологов сходство развития процесса. После вселения наблюдается переходный режим в форме сценария затухающих отдельных пиков численности, которые мы обсудим в следующей работе.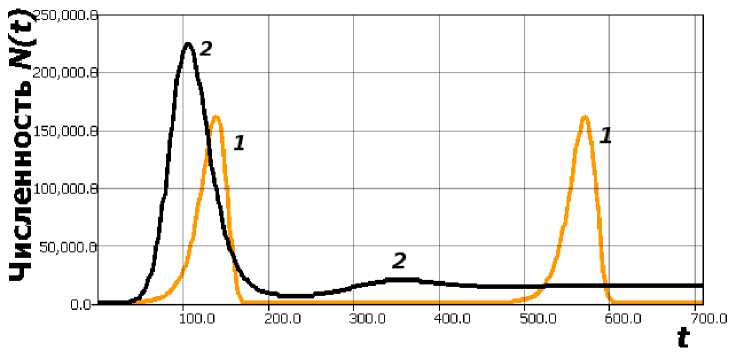
Список литературы Сценарии осцилляций и гибели в новой непрерывной модели эруптивной фазы инвазии чужеродного вида
- Кащенко, C. А. Динамика логистического уравнения, содержащего запаздывание/C. А. Кащенко//Математические заметки. -2015. -Т. 98. -C. 85-100.
- Переварюха, А. Ю. Разрушение релаксационных колебаний в новой модели экстремальной динамики численности популяции/А. Ю. Переварюха//Вестник Волгоградского государственного университета. Серия 1, Математика. Физика. -2017. -№ 1 (38). -C. 55-65. - DOI: 10.15688/jvolsu1.2017.1.6
- Perevaryukha, A. Yu. A model of development of a spontaneous outbreak of an insect with aperiodic dynamics // Entomological Review. — 2015. — Vol. 95,
- № 3. — P. 397–405. DOI: 10.1134/S0013873815030124
- Perevaryukha, A. Yu. Modeling the phenomenon of collapse of the exploited fish
- population with stochastic uncertainty / A. Yu. Perevaryukha // Theory of Probability and Its Applications. — 2018. — Vol. 62, № 4. — P. 659–660. DOI: 10.1137/S0040585X97T988861
- Reznik, S. Ya. Influence of target plant density on herbivorous insect oviposition choice: Ambrosia artemisiifolia L. (Asteraceae) and Zygogramma suturalis F. (Coleoptera, Chrysomelidae) / S. Ya. Reznik // Biocontrol Science and Technology. — 1993. — Vol. 3,
- № 6. — P. 105–113.
- Baker, T. Computing stability regions Runge - Kutta methods for delay differential equations / T. Baker, H. Paul // IMA Journal of Numerical Analysis. - 1994. - Vol. 14, № 4. - P. 347-362
- Bazykin, A. D. Nonlinear Dynamics of Interacting Populations / A. D. Bazykin. - L.: WSP, 1998. - 198 p.
- Birch, D. A New Generalized Logistic Sigmoid Growth Equation Compared with the Richards Growth Equation / D. Birch, T. Colin // Annals of Botany. - 1999. - Vol. 83, № 6. - P. 713-723.
- Deng, B. Food chain Chaos due to Shilnikov's orbit / B. Deng, G. Hines // Chaos. - 2002. - Vol. 12, № 3. - P. 533-538.
- Finley, C. Maximum sustained yield: a policy disguised as science / C. Finley, N. Oreskes // ICES Journal of Marine Science. - 2013. - Vol. 70, № 2. - P. 245-250. -
- DOI: 10.1093/icesjms/fss192
- Gilg, O. Climate change and cyclic predator - prey population dynamics in the high Arctic / O. Gilg, T. Sittler // Global Change Biology. - 2009. - Vol. 15, № 11. - P. 2634-2652. -
- DOI: 10.1111/j.1365-2486.2009.01927.x
- Gopalsamy, K. Time lags in a "food-limited" population model / K. Gopalsamy, M. Kulenovic, G. Ladas // Applicable Analysis. - 1988. - Vol. 31, № 3. - P. 225-237
- Hutchinson, G. An Introduction to Population Ecology / G. Hutchinson. - New Haven: Yale University Press, 1978. - 234 p.
- Klein, D. The Introduction, Increase, and Crash of Reindeer on St. Matthew Island / D. Klein // Journal of Wildlife Management. - 1968. - № 2. - P. 250-265.
- Kolesov, A. A modification of Hutchinson's equation / A. Kolesov, E. Mishchenko, Yu. Kolesov // Computational Mathematics and Mathematical Physics. - 2010. - № 12. - P. 1990-2002.
- Loehle, C. Catastrophe theory in ecology: a critical review and an example of the butterfly catastrophe / C. Loehle // Ecological Modelling. - 1989. - № 2. - P. 125-152.
- Miller, D. Matthew Island reindeer crash revisited: Their demise was not nigh - but then, why did they die? / D. Miller // Rangifer. - 2005. - № 4. - P. 185-197.
- Nenzen, H. Epidemiological landscape models reproduce cyclic insect outbreaks / H. Nenzen // Ecological Complexity. - 2017. - Vol. 31. - P. 78-87. -
- DOI: 10.1016/j.ecocom.2017.04.004
- Odum, H. T. Systems Ecology / H. T. Odum. - N. Y.: Wiley, 1983. - 644 p.
- Piyaratne, M. Catastrophic behavior of aphid population dynamics: An analysis of swallowtail model / M. Piyaratne // Computational Ecology and Software. - 2014. - Vol. 4, № 3. - P. 135-146. -
- DOI: 10.0000/issn-2220-721x-compuecol-2014-v4-0012
- Pikitch, E. Status, trends and management of sturgeon and paddlefish fisheries / E. Pikitch // Fish and fisheries. - 2005. - Vol. 6, № 3. - P. 233-265. -
- DOI: 10.1111/j.1467-2979.2005.00190.x
- Perez, L. ForestSimMPB: A swarming intelligence and agent-based modeling approach for mountain pine beetle outbreaks / L. Perez // Ecological Informatics. - 2011. - Vol. 6, № 1. - P. 62-72. -
- DOI: 10.1016/j.ecoinf.2010.09.003
- Post, E. Global Population Dynamics and Hot Spots of Response to Climate Change / E. Post // BioScience. - 2009. - Vol. 59, № 6. - P. 489-497. -
- DOI: 10.1525/bio.2009.59.6.7
- Sakanoue, S. Extended logistic model for growth of single-species populations / S. Sakanoue // Ecological Modelling. - 2007. - Vol. 205, № 1. - P. 159-168. -
- DOI: 10.1016/j.ecolmodel.2007.02.013
- Verner, J. Continuous explicit Runge - Kutta methods of order 5 / J. Verner, M. Zennaro // Mathematics of computation. - 1995. - Vol. 64, № 11. - P. 1123-1146. -
- DOI: 10.1090/S0025-5718-1995-1284672-4
- Voulgaris, S. Stochastic modeling and simulation of olive fruit fly outbreaks / S. Voulgaris // Procedia Technology. - 2013. - Vol. 8, № 4. - P. 580-586. -
- DOI: 10.1016/j.protcy.2013.11.083
- Wan, H. Biology and natural enemies of Cydalima perspectalis in Asia: Is there biological control potential in Europe? / H. Wan // Journal of Applied Entomology. - 2014. - Vol. 138, № 10. - P. 715-722. -
- DOI: 10.1111/jen.12132
- Wang, W. An Epidemic Model with Population Dispersal and Infection Period / W. Wang // SIAM Journal on Applied Mathematics. - 2006. - Vol. 66, № 4. - P. 1454-1472. -
- DOI: 10.1137/050622948
- Yeakel, D. Generalized modeling of ecological population dynamics / D. Yeakel // Theoretical Ecology. - 2011. - Vol. 4, № 2. - P. 179-194. -
- DOI: 10.1007/s12080-011-0112-6


