Сценарий невынужденной деструкции популяции в модификации уравнения Хатчинсона

Варианты моделей асимптотической динамики популяций для стационарного или периодически возмущенного репродуктивного потенциала, развиты достаточно подробно, но существует проблема, анализа, ряда, экстремальных плохо прогнозируемых явлений в экологических процессах, которые входят в противоречие с базовыми принципами регулирования численности.

Ограниченность пределов роста, численности популяции - один из таких ключевых принципов для системной экологии [1]. Первой популяционной моделью ограниченного роста, стала, модель Ферхюльста. 1838 г. Асимптотика, решения уравнения подразумевала, плавный выход численности к стационарному состоянию K, соответствующему балансу со средой:

dN = rN 6 - dt          K

N (t) =

N (0ДГ

1 + N (0)(e^rt - 1)/K ‘

r фическим данным европейских стран и уже тогда, предлагал модификации. Считающаяся хрестоматийной квадратичная саморегуляция численности в (1) не рассматривалась Ферхтольстом как единственно возможная для модели ограниченного роста. В 1845 г. он выписал такое обобщенное уравнение:

M-p = mp — np^. dt rK K r появились значительно позднее. Позднее он предположил [2], что динамика, народонаселения Европы развивается согласно (1) только до некоторого порога, так как не наблюдалось замедления темпов прироста, населения, которое для (1) должно происходить после N > K от плотности

— cN — 5N ²,

( N — или раздельно учесть смертность, зависящую иую cN много увеличив число параметров:

dN     γN ²

—— = Г---- dt y + ^N и получить дополнительно репеллерную точку равновесия

L) увеличив число ее путей скопления 5N ² и естоствеп-

L. что предложил Базыкии для видов с минимально допустимой численностью группы [3]. Отметим, что для формы правой части (1) f (N)(N — L) в вычислительных моделях еще необходима компенсирующая сверхбыстрый прирост перенормировка репродуктивного параметра: r1 « г, но вымирание N(t) ^ 0 выглядит слишком стремительным и безвозвратным явлением.

Многие популяции могут брать начало от нескольких сохранивших репродуктивную активность особей и через некоторое время демонстрировать режимы сложных флуктуаций. С вселения единичных особей начались регулярные нашествия европейского кукурузного мотылька. Ostrinia nubilalis в Северной Америке и затянувшаяся с 2012 г. вспышка. дальневосточной самшитовой огневки CydaUma perspectaUs в Краснодарском крае. Исчезновение ряда, популяций (характерно для островных сообществ, где нет разреженной границы ареала) может происходить как раз не из состояния близкого к неустойчивой L. но из благополучной окрестности балансовой емкости K. Мы ставим задачу получения в модели режима, соответствующего частному, но значимому сценарию популяционной динамики. Например, из-за. истощения пригодной растительности следующее крайне многочисленное поколение вредителей вдруг оказывается последним, и так часто заканчивается многолетняя вспышка, численности.

• 2.    Проблема популяционных автоколебаний

  Решения (1) и (2) плохо согласовывались с наблюдавшимися разнообразного вида, флуктуациями популяций самых разных животных. Флуктуации регистрируются даже для слонов в Национальном парке Крюгера, потому приходится проводить отстрелы с целью удержать популяцию в оптимальном по расчетам для сохранения растительной среды состоянии [4]. Слоны способны стремительно достигать пиковых значений N > 9000. тогда, как для них рассчитано K = 7000. Хотя согласно экологической тео- K

• 3.    Развитие уравнения (1) с запаздыванием

стремящейся к асимптотическому равновесию N ^ K ±е. Признаков уравновешивания у расчетного предела K не наблюдается и после изъятия особей. Через некоторое время после отстрела слоны начинают вновь оказывать чрезмерное давление на растительность. Лемминги считаются примером r-стратегии с нерегулярностью своих больших пиков, но вспышки грызунов для арктических экосистем с редкой растительностью из полярных кустарничков тундры эквиваленты воздействию слонов на. леса. Колебательная динамика. популяции может оказываться неустойчивой. Для гренландского лемминга, давно были известны популяционные циклы значительной амплитуды, которые внезапно завершились после серии пиков в конце XX века, и в настоящее время популяция леммингов мало изменяется на. низком уровне численности [5].

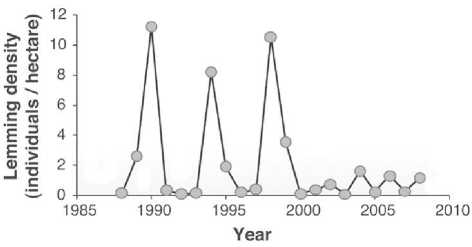
Рис. 1. Неустойчивость популяционного цикла лемминга.

Модель взаимодействия двух видов Вольтерра, как хорошо известно, позволяет получить циклическое решение системы двух дифференциальных уравнений. Казалось бы, уравнения позволяют формализовать колебания с отставанием по фазе, наблюдаемые в сообществе «зайцы - рыси». Как было установлено позднее, цикличность численности канадских зайцев обнаружена, и в регионах, где их враги не обитают. Более того, аналогичные квазигармонические колебания свойственны многим другим северным популяциям грызунов, в том числе обособленным островным группам, и которые по экологическим причинам не могут быть описаны исходя из модели взаимодействия двух видов типа, «хищник - жертва». Не подтвердились выводы об устойчивых колебаниях из модели Вольтерра. в лабораторных экспериментах Г. Гаузе с простейшими организмами. Колебания в лабораторных экспериментах с насекомыми получил С. Утида, но для взаимоотношений вида, «паразит -хозяин». Паразитизм имеет отличия от трофического взаимодействия «хищник — жертва», так как текущая динамика, численности паразитической осы зависит от количества, доступных яиц (но не взрослых жуков) в предшествующем поколении.

Из лабораторных экспериментов энтомолога. Никольсона. [6] стало понятно, что колебания численности могут появляться у изолированных популяций, обитающих при постоянных условиях и получающих фиксированное количество корма.

Хатчинсоном [7] была, предложена, модификация (1), исходя из запаздывающего действия регуляции в размножении дафний, что привело к уравнению с отклоняющимся по времени аргументом «logistic DDE»:

dN dt

= rN ( t ) 1 —

N (t — т ) \ k ) ■

τ зования и восстановления ресурсов или накопления/распада отравляющих продуктов метаболизма.

Возникающие в уравнении режимы поведения траектории были подробно исследованы во многих работах, в том числе отечественных [8]. При малых значениях запаздывания т динамика, модели опишет затухающие колебания N (t) ^ K. В (3) установлена, возможность возникновение бифуркации Андронова. - Хопфа. с появлением устойчивого предельного цикла N (t,r) Нарушение устойчивости состояния равновесия зависит от величины гт. Дальнейшее увеличение гт >  ^п вызывает переход в режим релаксационных колебаний. Быстрое возрастание амплитуды колебаний выраженной негармонической формы при увеличении временного промежутка, между максимумами и минимумами, стремящимся к неотличимым от нуля значениям, приводят такой релаксационный цикл (рис. 2) к затруднениям при экологическом обосновании.

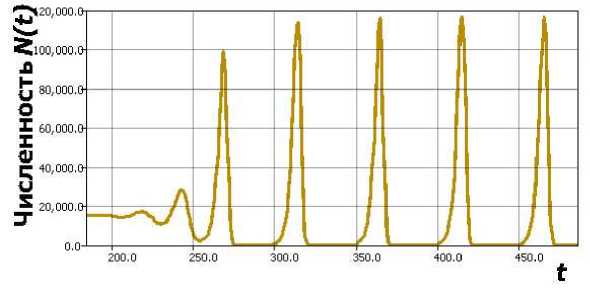
Рис. 2. Релаксационный цикл в уравнении (3), K = 15000.

Многим насекомым свойственны продолжительные вспышки численности, но они начинаются после преодоления некоторого порогового значения, когда, паразиты не могут эффективно подавлять размножение. Формы колебаний для автохтонных и инвазионных популяций могут быть различными. Помимо затухающих и гармонических колебаний может возникать и противоположное явление - возникновение флуктуации с затяжными пиками численности. Такая ситуация возможна, например, при переходе некоторых популяций к каннибализму и/или может быть обусловлена, изменением направления естественного отбора, в особых условиях существования. Дополнение «репродуктивного» сомножителя запаздыванием rN(t - т)f [N(t),N (t - т )] не несут экологического смысла.

В [9] рассматривалась модификация модели Хатчинсона, (с приведенными коэффициентами):

d- = AN(t)f (N(t - 1)) ,(4)

dt где f (•) - дифференцируемая функция, разложимая в асимптотический ряд, для которой выполняются условия f (0) = 1, f (x) = -ao + XX ak, x '   ■. > 0.(40)

k=1 xk

Условиям (40) соответствует, например, предложенная ранее в [10] для тех же целей функция f '_.<Г)

(1 + cx)

В подобной модификации (известной как «food-limited DDE») расширяется число параметров, определяющих характеристики релаксационного цикла, неклассической формы, так как при увеличении c в (4⁰⁰) сжимается амплитуда.

Из дополнительных ограничений при преобразовании исходного уравнения (4) к сингулярно возмущенному x = F(x(t — 1),е) и далее к предельному релейному уравнению с запаздыванием x = R(x(t—1)) предполагается А » 1. Для (4) с (40) утверждается существование единственного орбитально экспоненциально устойчивого цикла. По-прежнему непонятно какой именно нелинейный популяционный процесс может помочь предсказать свойство (4), так как из утверждения о свойствах цикла, в [9] получено min N*(t, А) ~ C1 exp (—Аао), C1, ao = const > 0, и, как отмечено ранее, А изначально указывается достаточно большим значением. При использовании функции (400) наши вычислительные эксперименты показывают влияние демпфирующего колебания параметра c на все характеристики цикла, что напрямую не обсуждается в [9]. и требуется условие c » 1. так как при малых c свойства, цикла (4) будут значительно менее интерпретируемы, чем в (3).

Для (3) и (4) установлено свойство диссипативности траектории:

N (t) 6 ехр(гт).

∗

• 4.    Модель динамики вспышек листовертки

  Некоторым популяциям вредителей свойственно специфическое нерегулярное явление пилообразной вспышки численности «sawtooth oscillations» [И], которую мы можем описать при дополнении модели (4), (4". После равновесного состояния при численности бабочек, не вызывающей дефолиации, вдруг появляется серия непоследовательных очень многочисленных поколений, на порядок превышающих среднемноголетнюю численность за. предшествующую декаду в очаге вспышки. Так внезапно проявляет себя еловая листовертка. Choristoneura fumiferana в лесах Северной Америки (на. рис. 3 - изменение площади погибшего леса, с тремя выраженными пиками по данным [12]), где более 30 лет постоянно наблюдалась полная потеря хвои (дефолиация) на. значительных площадях вплоть до прекращения вспышки в конце 1980-х гг. Завершение атипичной вспышки может происходить так же внезапно, как и ее развитие.

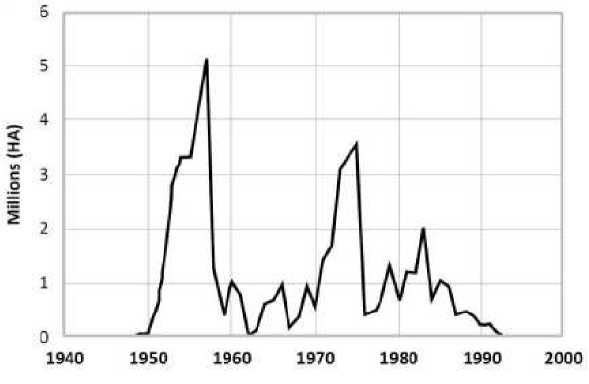
Рис. 3. Пилообразная вспышка листовертки в масштабах гибели леса.

Мы можем предложить математическое описание такого частного, но весьма неблагоприятного для лесного хозяйства, сценария популяционной динамики, увеличив степень 00

dN =      ( ^K - ^N2^(t - т )

dt       (t) (K + cN ³(t - т )) ■

Так удается сгладить недостаток у минимумов minot N* (t, г) ^ е, е ^ 1, слишком низких для возможностей повторного быстрого роста, численности при свойственных вредителям больших г. но отойдя (>т условий (40): f(x) ^ 0. x ^ +то. В вычислительных исследованиях для (5) мы после бифуркации можем получить реализацию сценария пилообразной вспышки (рис. 4). Основной значимый аспект (5) — очередной стремительный неконтролируемый рост численности начинается от значения близкого к существовавшему перед бифуркацией равновесию, оптимального баланса, со средой. Не хватает у всех аналогичных модификаций уравнений с запаздыванием некоторых триггерных свойств, чтобы рассматривать аспекты быстрого сценария самозавершения вспышек.

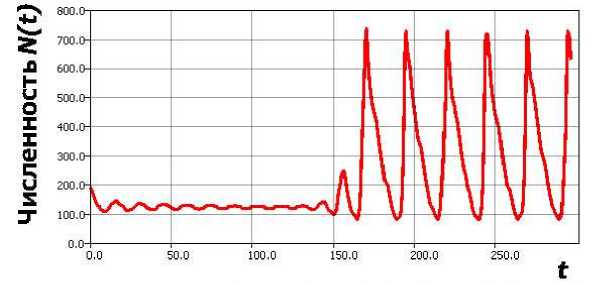
Рис. 4. Переход к релаксационному циклу в повой модели (5).

Замечание. Известно, что в итерациях нелинейных функций Rj+i = ^(Rj ), имеющих максимум ^(Rm) = 0, <(Rm) = 0, поведение траектории даже более разнообразно. В ихтиологии применяется:

Rj+1 = aRj e-bRj, a > 1, 0  e2 возникают циклы разнообразных периодов, и дискретизация задачи поможет найти оптимальное решение. Однако, помимо периода, циклы итераций отличаются взаимным расположением точек. При бифуркациях удвоения периода, вокруг теряющей устойчивость циклической точки возникнут две новые, сохраняя симметрию ветвей на. бифуркационной диаграмме сценария Фейгенбаума. Короткие циклы грызунов в таких терминах — это монотонные перестановки с пиком в конце, которые можно найти в «окнах периодичности» с циклами p = 2i очень узких диапазонах значений управляющего параметра. [13]. Существует ряд причин, по которым возникновение хаотического аттрактора. в точке накопления каскада, бифуркаций удвоения не является хорошим свойством для описания популяционных процессов.

• 5.    Модификация с предкритическим порогом

• 6.    Вычислительный анализ новой модели

  При малом значении запаздывания в (6) получаем затухающие осцилляции с N ^ H. При увеличении т пли r1 в таком уравнешш (с r1 = 10^-3г) возникнет притягивающий никл (рис. 5. K = 15000. H = 5000).

Из развития уравнения (3) можно получить описание еще одного специфического экологического явления, которое не было рассмотрено в известных работах. В случае вспышек насекомых-фитофагов понятие емкости экологической ниши из (1) утрачивает смысл, а. равновесие при малой их численности имеет другую природу. Из анализа, дилеммы парка. Крюгера, предположим существование некоторого предкритического порогового уровня H <К. Для генерирующих вспышки популяций нижний критический порог полагается весьма малым L « H. Положим, что достижение значения численности K означает не уравновешивание, но деградацию необходимой составляющей среды обитания. Переход через мягкий порог имеет значение для механизмов контроля внутри-популяционной структуры. Тогда, на. динамику системы оказывает влияние отклонение [H - N (t - т )], притом величина отклонения может быть как положительной, так и отрицательной. Модифицируем (3) следующим образом:

dN = ri N ^¹ — N ⁽ t - ^T ) ) (H — N(t — т )) • dt K

Можно считать, что при смене знака, отклонения члены правой части (воспроизводства, и регуляции) меняются своими функциональными ролями в модели. Для правой части (6) нс выполняются условия (40). указанныс для f (x) при обосновании утверждения о единственном орбитально устойчивом цикле, потому не обязательно теорема. (2.1) из [9] будет полностью справедлива, в нашем случае.

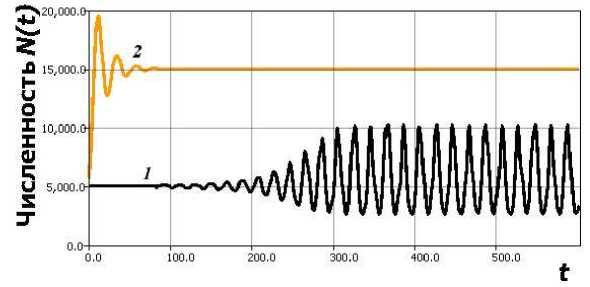
Рис. 5. 1 — цикл после бифуркации в (6), 2 — динамика (3) при аналогичных параметрах.

На рис. 5 динамика, после плавного прохождения бифуркационного изменения по сценарию Андронова - Хопфа при переходе r1 через критическое значение (в вычислительном эксперименте рис. 5 все параметры модели сохраняются), показывающая уста-новленпе никла при N (0) = H + б. H = 5000. K = 15000.

Цикл быстро становится релаксационным с возрастанием r1, из имеющейся, например, в [14] теории о модификациях logistic DDE мы не можем подтвердить его глобальную устойчивость. Амплитуда, колебаний в отличие аналогичного случая модели (3) не возрастает до нереалистичных величин, но остается в разумных для биологии границах. Скошенная форма, пиков даже более похожа, на. реальные данные популяционной динамики. В (6) при N(0) < H переход к установившимся флуктуациям происходит не плавно, но через скачкообразный переходный режим.

При дальнейшем увеличении значения г1т произойдет другое резкое изменение поведения траектории, которая перестанет притягиваться к замкнутому подмножеству фазового пространства. Изменение репродуктивного параметра, можно трактовать как следствие ослабления давления паразитов на. выживаемость личинок. Если давление ослабнет совсем, то при такой бифуркации траектория системы до установления цикла, со своей увеличивающейся огромной амплитудой может быть резко выброшена, за. пределы допустимых для ее существования значений при N(t - т ) > K. Такая потеря установившегося режима, считается жесткой (катастрофической). На рис. 6 ситуация после бифуркации, когда в результате изменения параметра r1 (в сравнении с аналогичным изменением r в (3) в момент t = 150) траектория в релаксационных колебаниях преодолевает значение K, и далее N(t) ^ то реализует сценарий кризиса перенасыщения, появления последнего сверхмногочисленного поколения и деструкцию всей биосистемы.

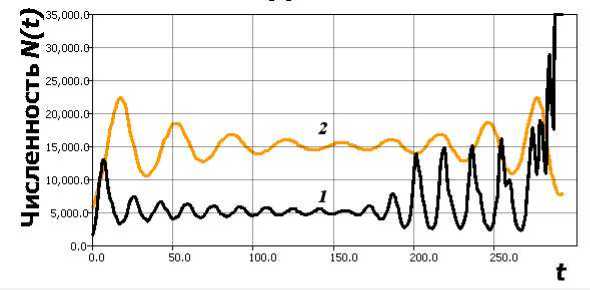
Рис. 6. 1 — выброс за границы емкости среды в (6), 2 — динамика (3) при аналогичном изменении параметра.

Цикл сжимается и выбрасывается, вычислительный эксперимент заканчивается сообщением программы о переполнении при вычислениях с плавающей точкой. ∗

• 7.    Проблема обобщения всех модификаций (3)

Выглядит перспективным объединение идей двух предложенных модификаций, но не все варианты, возникающие в уравнениях, с запаздыванием имеют прикладной экологический смысл. Можно представить обобщенное уравнение в следующем виде:

dN

ИГ = ^{XN (t)}

K - N2(t - т ) (K + cN 3(t - т ))

(H - N(t

-

^т )),

увеличивая нелинейность в правой части до кубической. Тогда, образующая для N (0) <  H релаксационный цикл траектории при уменьшении с начнет достаточно параболически плавно и неограниченно возрастать (рис. 7, с₀ = 0.11, бифуркационное с = 0.1, т = 8).

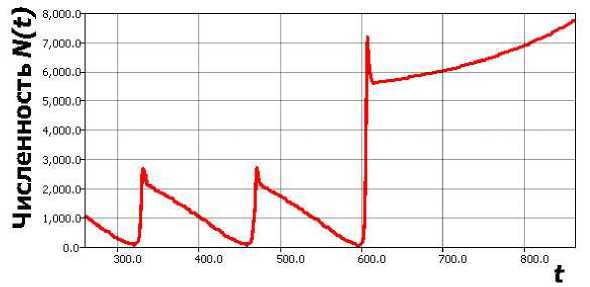
Рис. 7. Медленный сценарий ухода траектории из цикла в (7).

Подобный путь потери решением свойства диссипативности видится экологически не обоснованным и сценарий популяционной динамики вряд ли реализуется. Мы рассматривали ситуацию изолированной саморегулируемой популяции, потому должно присутствовать ограниченное сверху предельное состояние (цикл или равновесие), либо происходит деструкция биосистемы скачкообразно.

Авторы [10], пытаясь преодолеть отмеченные недостатки, в дальнейшем расширили модель (4). (4⁰⁰) до системы. где параметры A. c становятся изменяющимися с периодом ш функциями (обусловленными сезонностью характеристик среды обитания) и f (N(t - тш)). Однако в лабораторных экспериментах с насекомыми Никольсона и Утиды не вносились никакие вынуждающие воздействия. Для кукурузного мотылька. Ostrinia nubilalis на. Юге России свойственна, динамика, с серией резких пиков численности, перемежающаяся с годами длительной депрессии популяции, которую иногда связывают с цикличностью активности магнитного поля Солнца, но физического объяснения эффекту пока, не получено. Потому актуально модельное описание именно внезапного возникновения специфических популяционных автоколебаний вредителей.

• 8.    Заключение

  Предложена, модель возникновения популяционных колебаний релаксационной формы, где вместо дальнейшего увеличения амплитуды происходит выброс траектории в режим за. рамками ограниченного прироста, численности. Будем считать введенное в уравнение значение H мягким пороговым состоянием отложенного действия, в отличие от явной нижней критической точки Lb (2) и жесткого уровня остановки прироста K в (1). Емкость среды не выступает более асимптотическим предельным значением для затухающих осцилляций. В новой модели критическим, но спонтанно преодолеваемым состоянием служит K. N > K на. время 5t > т подразумевает стремительное катастрофическое разрушение популяцией своей среды обитания. Пример катастрофы успешно размножавшейся искусственно вселенной популяции - судьба, исчезнувших оленей на. острове Беринга, куда, в 1882 г. было завезено 15 голов, через 20 лет их численность колебалась 1,5-3 тыс. с учетом промысла. Без регуляции к 1917 г. на. острове не осталось оленей, обильные лишайниковые пастбища, были полностью истощены. В демографии самый известный случай кризиса, перенаселения — загадка, падения цивилизации острова. Пасхи.

Таким образом, мы получили вычислительную модель, описывающую переход численности из окрестности неявного порога, в устойчивый режим колебаний. В современном обзоре по применению уравнений с запаздыванием [15] в математической биологии сценарий с разрушением автоколебаний не рассматривался. Бифуркация, для которой требовалосв изменение условий регуляции, приводит систему не к изменению ампли-туды/периода цикла, или переходу к хаотическому движению, но к скачку за. границы экологического баланса, в виде резкой потери замкнутого колебателвного контура. Полученные при исследовании уравнения характеристики достаточно особых случаев популяционного процесса, не могут, по нашему мнению, быть распространены на. обобщенный случай динамики распространения вида-вселенца. Модификация модели (6) с медленной потерей переходного циклического режима, не получает содержательной популяционной интерпретации.