Сценарные расчеты стратегий развития региона

В официальных документах, таких как Стратегия социальноэкономического развития Сибири до 2020 года, Стратегия социальноэкономического развития Дальнего Востока и Байкальского региона на период до 2025 года, ФЦП «Охрана озера Байкал и социальноэкономическое развитие природной территории на период до 2020 года», содержатся весьма общие количественные показатели и данные, отражающие цели и стратегии развития региона либо в экономических терминах, либо в терминах сохранения уникального природного объекта, однако отсутствуют комплексные социо-эколого-экономические оценки последствий этих программ. Одна из причин – отсутствие официально признанной методологии таких оценок.

Разрабатываемый с середины 1970-х годов информационнокомпьютерный инструментарий [1-3] может служить своего рода «лабораторным прототипом» такой методологии. Одна из его последних версий, полученная в ходе естественной многолетней эволюции, наиболее адаптирована к реальной ситуации острого дефицита междисциплинарной информации о взаимодействии экономической, природной, социальной и инновационной подсистем единой сложной системы, каковой является регион, что отражено в работах [2-3].

Рассматриваются сравнительные сценарии развития региона с использованием концептуальной модели региона [2] по данным, сформированным на примере бурятской части Байкальского региона. Они реализуются в вычислительных экспериментах с несколькими модификациями модели: полностью агрегированными эколого-экономическими и так называемыми базовыми, отражающими укрупненно структуру экономики, природной и социальной компонент. Эти модификации получаются при соответствующих допущениях и наборах данных из полной концептуальной модели.

1.    Основная социо-эколого-экономическая модель и оптимизация управляющих воздействий с = (E - A)y - Bu - Az - Bzuz - Avv - Bvuv,

r = r + N(r - r) - Cy + z + imr - eX,

k = u - [ 5 ] k , k z = u z - [ 5 z ] k^z , k v = u v - [ 5 v ] k v ,

0 <  y <Г ( k ) ,0 <  z ^z ( k z ),0 <  v v ( k v ),

9 = -([v ]+ Hnv + Hdf )(9 - 6 ), 0(0) = 0,

Здесь y , z, v – векторы выпусков продукции по отраслям, активного природо-социо-восстановления, активных инноваций, c – конечное по-zv       zz vv      z v      z v требление; (k, k , k ), (Г(k), Г (k ), Г (k )), (u, u , u ), (5, о , о ) -основные фонды, мощности и инвестиции (векторы) и темпы амортизации в экономическом, природо-социо-восстановительном и инновационном секторах (диагональные матрицы); p– матрица-строка цен (ценовых поправок); r – вектор индексов состояния природной среды и социума; θ – вектор инновационных индексов (агрегированное описание изменения за счет инноваций элементов матриц A, Az , B, Bz , C и других параметров); r(t) – заданная функция (опорная), например получаемая из статистического прогноза; imr , ex r – миграционные потоки загрязнений и ресурсов; A, Az , Av – матрицы прямых затрат в экономическом, приро-до-социо-восстановительном и инновационном секторах; B, Bz , Bv – матрицы фондообразующих затрат в указанных секторах; N – матрица коэффициентов взаимовлияния компонентов природной и социальной подсистем; C – матрица коэффициентов прямого воздействия отраслей экономики на компоненты природной и социальной подсистем; Hinv , Hdif – матрицы, отражающие влияние инвестиций и диффузии иннова- ций; выражение вида [X ] – диагональные матрицы, построенные из компонент вектора X .

Цель проводимых расчетов – провести сравнительный анализ долгосрочных последствий стратегий развития подобного типа для всей социо-эколого-экономической системы региона и показать важность оптимизации управленческих решений для формирования стратегии, отвечающей принципам современной парадигмы устойчивого развития. В задаче оптимального управления y , u , z , v , u ^z , u ^v играют роль управлений, а в качестве критерия оптимальности рассматривается максимум благосостояния – накопленного регионального дохода за вычетом штрафа s ( r ) за социо-экологические нарушения на заданном временном интервале при заданных начальных условиях:

tF n=J (pc - 5 (r )e-ptdt, k (0) = k0, r (0) = Го, 0(0) = 0,               (6)

где p – прогнозируемая цена (ценовая поправка), ρ – коэффициент дисконтирования. Величина штрафа характеризует предпочтения в критерии благосостояния.

В [5] находятся магистральные решения как идеализированные при предположениях о неограниченности линейных управлений, что позволяет перейти к достаточно простым производным системам, известным из теории вырожденных задач и использовать их как основу эффективного сценарного анализа. Подобный подход успешно использовался в [6-7].

2.    Типы сценариев и основные данные для сценарных расчетов

Сценарные расчеты проводились по нескольким группам сценариев:

• 1)    инерционные, сохраняющие сложившиеся тенденции,

• 2)    оптимизационные без инноваций,

• 3)    инновационные.

В каждой группе рассматривались варианты с предпочтениями экономике или экологии, в т.ч. предпочтение экономике с учетом ущербов от экологических нарушений, варианты без учета и с учетом роста восстановительных мощностей, варианты с учетом неопределенностей в инновационном блоке и оценкой чувствительности модели к этим неопределенностям.

С использованием методики [8] были сформированы наборы данных для сценарных расчетов, представляющих две модели Бурятского региона: полностью агрегированную, где состояние каждой из взаимодействующих подсистем задается скалярным показателем, и базовую, в которой фигурируют векторные показатели небольшой размерности (табл. 1). Большинство сценариев просчитывалось на агрегированной модели, а затем избранные сценарии детализировались на базовой версии.

В агрегированном наборе данные экономического блока были получены в основном из официальной статистики. Данные для остальных компонент оценивались экспертным путем с непосредственным использованием методики компонентных абстрактных экспериментов.

Таблица 1

	Компоненты векторов (диагональных матриц) базового набора				Агрегированный набор
	1	2	3	4
k 0 (млрд р)	216,53	144	39,47	-	400
k 0 z (млрд р)	2,6	4	0,4	3	10
k 0 d (млрд р)	0,8	4,85	0,35		6
r	0,9	0,8	0,6	0,7	0,8
h г max	-	-	-	-	1
h г min	0	0	0	0	0
* r	1	1	1	1	1
θ	0	0	0	-	0
θ	1	1	1	-	1
γ ср	0,3	0,45	0,6	-	, = ВРП = 0,45 k 0
γ z	0,002	0,002	0,003	0,002	0,002
γ d	0,0001	0,00012	0,00015	-	0,00012
im r	0	0	0,0015	0	По смыслу
ex r	0	0	0,00025	0	По смыслу
p 0	1	1	1	-	Р ( 6 ) = p 0( 1 + v p 0 )
δ (diag)	0,05	0,05	0,05	-
δ z (diag)	0,05	0,05	0,06	0,05	0,05
δ d (diag)	0,05	0,05	0,05	-
Hdif (diag)	0,01	0,01	0,01	-	0,01
A 0	0,39	0,34	0,36	-	A о = 0,5 A = (1 - V a 6 )(1 - в ( r )) A o (с учетом экоущерба экономике)
	0,063	0,15	0,1	-
	0,047	0,01	0,04	-
B = Bz = Bd (по смыслу)	0	0	0	-	1
	1	1	1	-
	0	0	0	-
A 0 z	1412	1008	1080	1176	A 0 = 1500 По смыслу млрд р./1 A = (1 - vz0 ) A 0
	54	450	360	138
	34	42	72	186

A 0 v	360	480	420	-	A o = 1200 млрд р./1 A v = (1 -V v 0) A 0
	600	600	600	-
	240	120	150	-
C 0	3,5*10-6	0,7*10-6	0,7*10-6	-	C 0 = 7*10 - 6 c = (1 - v c e ) c 0
	1,5*10-6	3,5*10-6	1,4*10-6	-
	0	0	0	-
	2*10-6	2 *10-6	1,2*10-6	-
N	-0,003	0,08	-0,004	0,003	-0,006
	0	-0,007	-0,0002	0
	0	0,001	-0,008	0
		0,003	0	-0,001

Для расчета экономических данных базового набора использовались прямые расчеты показателей на основе статистических данных, например, по основным фондам, и абстрактные эксперименты в случае отсутствия статистических данных, например, при расчете матриц (массивов) воздействий отраслей на компоненты природной среды, социума и затрат на их восстановление.

Различные варианты получались за счет изменения соответствующих параметров основного набора табл. 1. Например, параметр штрафа s задавался малым или большим для сценариев с экономическими и экологическими предпочтениями соответственно. Наряду с благосостоянием подсчитывался чисто экономический показатель – накопленный региональный доход I , который по смыслу есть сумма благосостояния и накопленного штрафа I = П F + S .

3.    Результаты расчетов без роста восстановительных и инновационных мощностей

На рис. 1-4 представлены результаты расчетов при предположении, что для осуществления соответствующей текущей деятельности достаточно имеющихся восстановительных и инновационных мощностей (основных фондов).

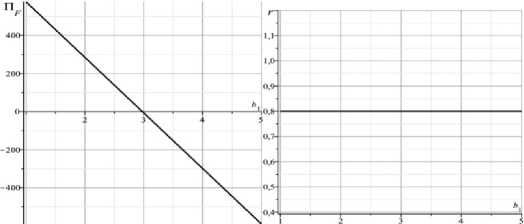
Рис. 1. Инерционный сценарий:

S =0, k F = k 0 , Y f = Y о , H =0, A v =2, a = 0,7, q = 2,2, b 2 = 1

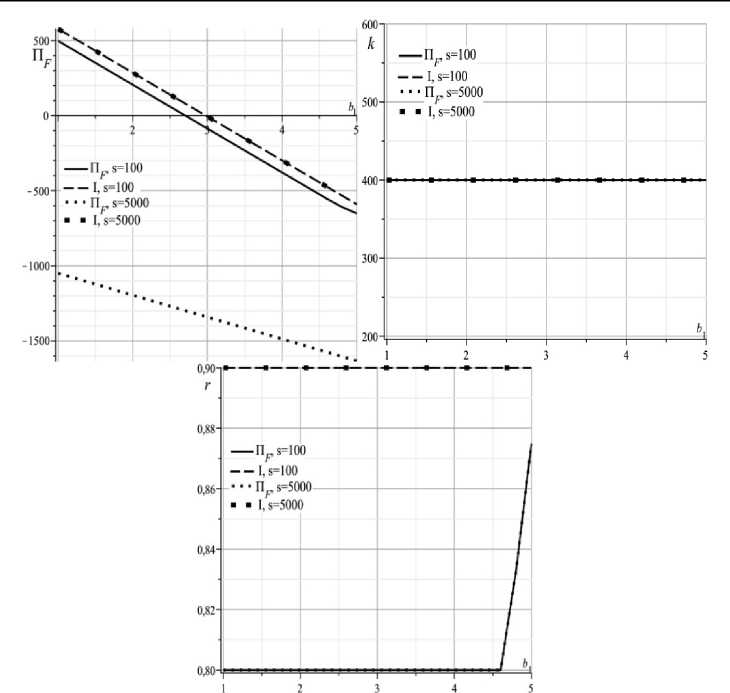
Рис. 2. Оптимизационные сценарии без инноваций: α = 0,7, q = 2,2, b ₂ = 1 с предпочтениями экономике: s =100, γ _F = γ ₀ , H =0,001, A ^v =2

и экологии s =5000, γ _F = γ ₀ , H =0, A ^v =2

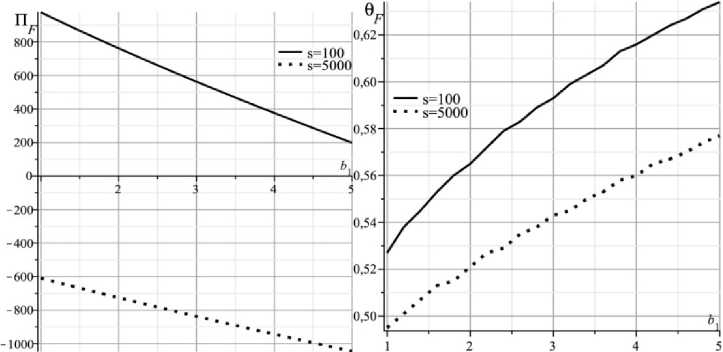
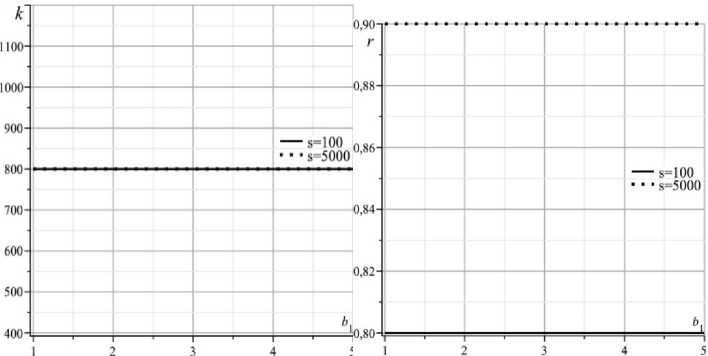
Рис. 3. Инновационные с предпочтениями, в том числе предпочтение экономике α = 0,7, q = 2,2, b ₂ = 1

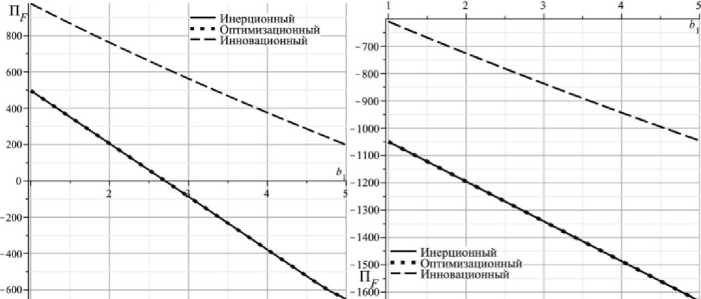
а) s = 100

б) s = 5000

Рис. 4. Сравнение трех типов сценариев при различных предпочтениях α = 0,7, q = 2,2, b ₂ = 1

Обратим внимание, что результаты для инерционного и оптимизационного сценариев совпадают, но сильно отличаются от инновационных. Это объясняется «плохими значениями» основных параметров, при которых инерционное развитие и оказывается оптимальным. Инновации открывают возможность улучшения этих параметров, что и приводит к существенному изменению выходных характеристик.

4.    Сценарии с учетом роста восстановительных и инновационных мощностей

В расчетах данного раздела штрафной коэффициент s принимался равным 0 для сценариев с предпочтениями экономике и s = 10000 – с предпочтениями экологии. Коэффициенты функции Кобба-Дугласа –

r ( k ) = вк ^а , α и β принимались равными 0,5 и 10 соответственно. Другие параметры, отличные от указанных в табл. 1, приведены ниже.

На представленных далее графиках показаны результаты для трех сценариев – оптимизационного, инновационного и инерционного.

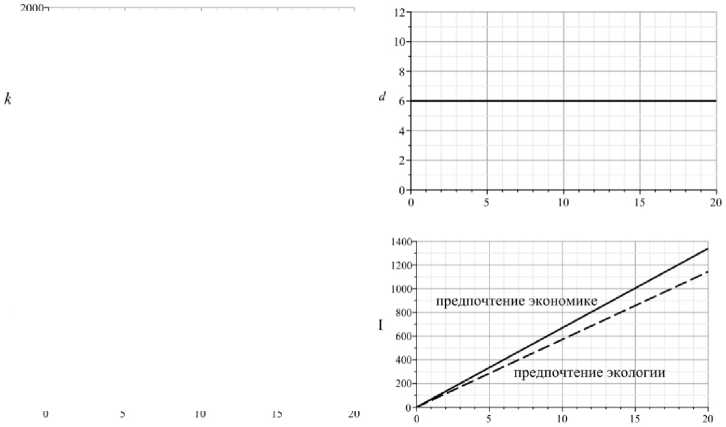
10000): 0 = O F = O ₀ = 0 , H = 0

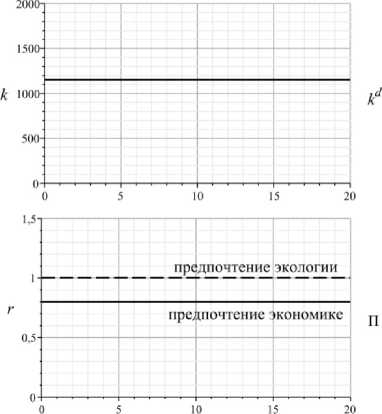
Рис. 5. Оптимизационные сценарии без инноваций с предпочтениями

экономике (s = 0)и экологии (s =

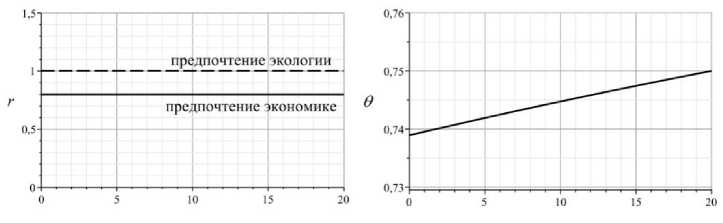
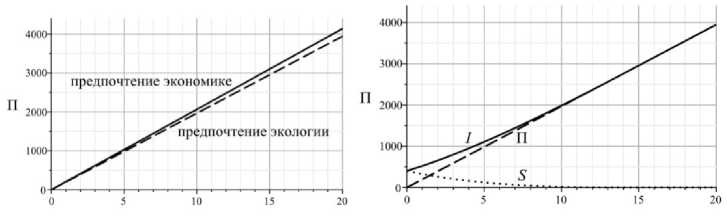
Рис. 6. Инновационные с предпочтениями экономике ( S = 0 ) и экологии(s = 10000 ): H = 0,01 , A^d = 2 k ₀

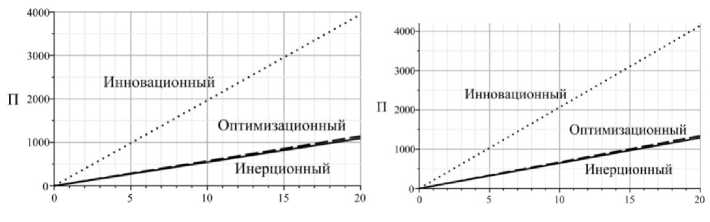
Рис. 7. Сравнение благосостояния для трех сценариев: инновационного, оптимизационного и инерционного

Полученные результаты на идеализированной версии модели далее уточнялись с учетом реальных ограничений, предусмотренных в полной версии (1) – (6), в универсальной итерационной процедуре, реализованной в C++ со специальным пользовательским интерфейсом.

На нижеследующих графиках пунктирной линией ( ) обозначены данные, полученные в результате аппроксимации идеального магистрального решения, а сплошной линией ( ) – данные, полученные в результате улучшения.

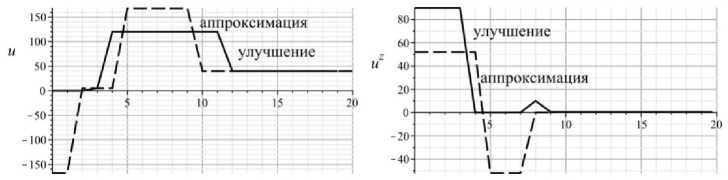
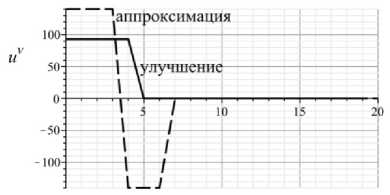
Рис. 8. Значения инвестиций u , u ^z , u ^v соответственно в экономическом, природо-социо-восстановительном и инновационном секторах

Республика Бурятия: основные данные

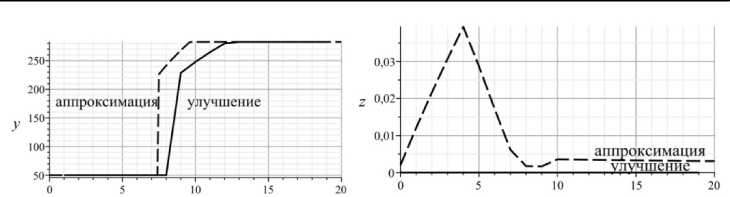
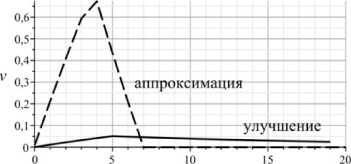
Рис. 9. Значения выпуска продукции y, активного природо-социо-восстановления z и активных инноваций v

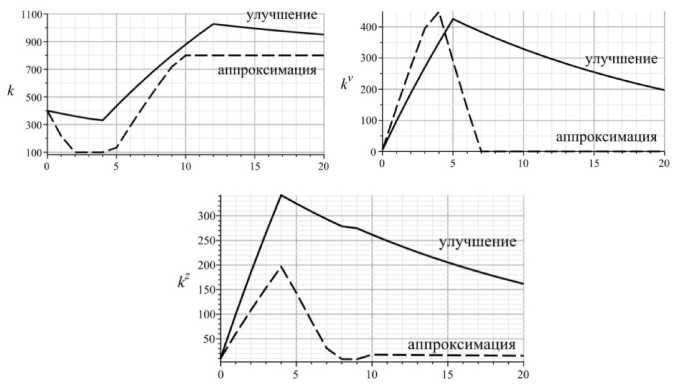
Рис. 10. Значения основных фондов в производственном k , социо-природовосстановительном kz и инновационном kv секторах

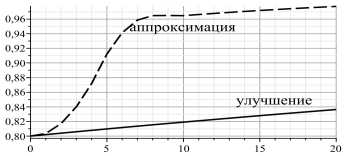
Рис. 11. Значения индекса состояния природной среды и социума r и инновационного индекса θ

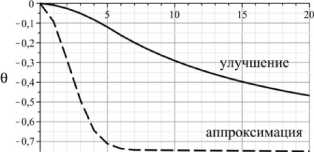
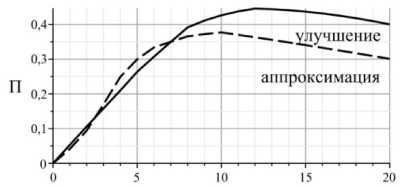
Рис. 12. Значение благосостояния

Улучшенный функционал по итерациям

Таблица 2

№ итерации	П F	№ итерации	П F
0	0,399525	5	0,400137
1	0,399899	6	0,400154
2	0,400015	7	0,400167
3	0,400076	8	0,400176
4	0,400113

5.    Учет неопределенностей и оценка чувствительности

Предполагалось, что инновации в модели носят случайный (стохастический) характер и от них зависят такие составляющие модели, как A, Av , Az , C . С учетом этого зависимости отдельных параметров от инновационных индексов определялись по формулам: хг = х0 (1 + Oai), Xai = 1, i гдеαi – весовые коэффициенты, которые менялись случайным образом при заданном инновационном индексе.

Весь временной отрезок был разбит на четыре пятилетних этапа и заданы диапазоны изменения каждого αi в пределах от 0 до 1, эти величины выбирались с помощью датчика случайных чисел и нормировки полученной выборки, так как по условиям модели их сумма должна быть равной 1. Более детально методика изложена в [7]. Расчеты проводились для инновационного сценария с предпочтениями экономике и экологии (соответственно s=10, s=5000). Результаты представлены на рис. 14–15 (при случайных наборах αi ), сплошной линией даны средние значения функционала благосостояния.

На рис. 14 среднее значение функционала для 10 вариантов расчетов равно 1027,876, тогда как при средних значениях весовых коэффициентов 1029,795.

При увеличенном штрафном коэффициенте s (рис. 15) среднее значение функционала составило 1017,455 и при средних значениях α _i –

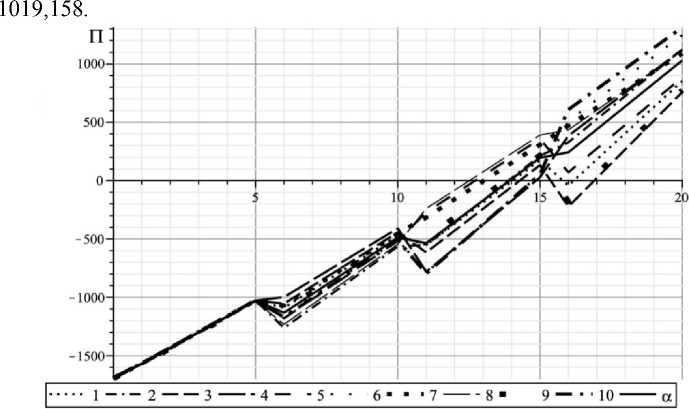
Рис. 14. Изменение благосостояния Π при случайном разбросе инновационного индекса, s=10

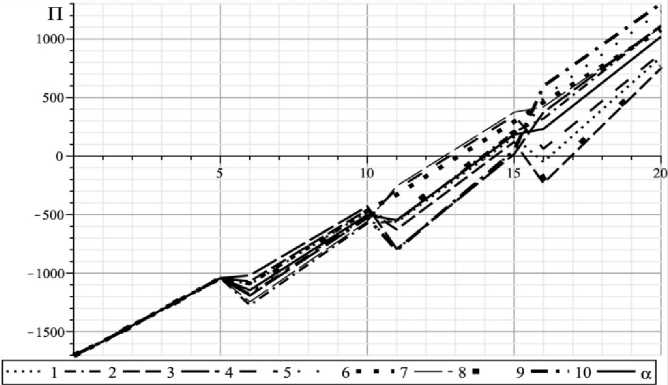
Рис. 15. Изменение благосостояния Π при случайном разбросе инновационного индекса, s=5000

Как видно из сравнения полученных результатов, несмотря на стохастический характер инноваций, среднее значение функционала благосостояния несущественно отличается от значения, полученного при средних значениях весовых коэффициентов при достаточно широком диапазоне его изменений.

Отметим, что для оценок расчеты можно вести как детерминированные по средним значениям весовых коэффициентов, что резко сокращает объем вычислений.

Заключение

В целом можно утверждать, что предложенный подход к комплексной оценке на основе сравнительного сценарного анализа себя оправдал. При этом важную роль играет именно наиболее агрегированные версии региональной модели, в которой матричные коэффициенты, содержащие большое число параметров, сводятся к числовым коэффициентам, допускающим достаточно простую содержательную интерпретацию.

Другой важный методический аспект – возможность получения простых расчетных соотношений для быстрых серийных вычислительных экспериментов исходя из специфики рассматриваемой задачи как вырожденной задачи оптимального управления. Соответствующая процедура преобразований непосредственно распространяется на многокомпонентные модели любой размерности, что дает возможность развивать далее эффективный инструментарий для более детальных оценок с использованием данного опыта.