Сдвиговые волны в круговой щелевой структуре пьезоэлектриков с вращающимся цилиндром

Было показано [1], что в структуре пьезоэлектриков со щелью могут существовать локализуемые ее границами электрозвуковые волны. В работах [2; 3] под влиянием запросов приборостроения и стремительно развивающейся робототехники эти результаты получили обобщение на случай, когда один из пьезокристаллов щелевой структуры приводится в относительное продольное перемещение. Выяснилось, что для антисимметричной моды щелевых волн достаточные для приложений изменения в спектрах вызываются сравнительно медленным относительным перемещением в несколько миллиметров за секунду. В настоящем сообщении рассматривается щелевая структура с постоянной кривизной границ, когда относительное перемещение пьезоэлектриков реализуется вращением пьезоэлектрического цилиндра в круговой полости другой пьезоэлектрической среды, покоящейся в лабораторной системе отсчета.

• 1.    Формулировка задачи

В представленной на рисунке геометрии задачи пьезоэлектрический цилиндр радиуса R и окружающая его пьезоэлектрическая среда с круговой полостью принадлежат к классу пьезоэлектриков 6mm (4mm, »m) с общей ориентаци- ей осей симметрии высшего порядка вдоль оси z цилиндрической системы координат (r, 0, z). Сдвиговые волны со смещениями u И z при избранной ориентации кристаллов сопровождаются электрическими полями в плоскости распространения и ввиду коллинеарности сдвиговых смещений вращающегося цилиндра u2 вектору его угловой скорости Q не подвержены в цилиндре влиянию инерционных сил (центробежные силы и силы Кориолиса). В итоге исходные уравнения пьезоакустики примут в лабораторной системе отсчета, привязанной к неподвижному-пьезоэлектрику (r > R), известный [4] вид р^ = XV2 u + e V^,

• d t ²

• ( д     d         „2„2

• P Hr + ^ I u2 = XV u2 + eV ф2,

^51

• „2      4 n e „2

• ^{V ф} 1,2 =---- ^{V u} 1,2 .

s

Здесь V — лапласиан в полярных координатах; р, X, e , s — плотность, модуль сдвига, пьезомодуль и диэлектрическая проницаемость пьезоэлектриков (цилиндр и окружающая его пьезоэлектрическая среда одинаковы по своим параметрам); t — время; Q — угловая скорость вращения цилиндра. Сдвиговые смещения u и электрические потенциалы ф нумеруются ниж-

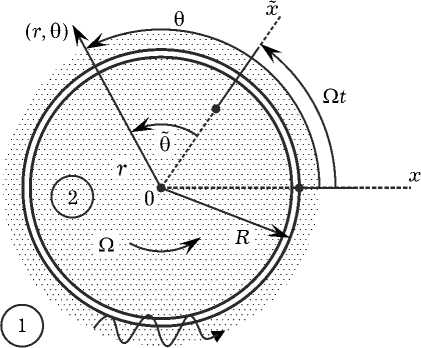
Рис. Геометрия задачи. Показаны полярные координаты, привязанные к кристаллам. Вакуумная щель между кристаллами полагается предельно тонкой

Z p [ln( J p (Z p ))]‘ =

I p\K ² ^[ln( H ^Q]'

I p|K ² + 2^[ln( H ^O]'.

Квадратными скобками со штрихами в (3) обозначены логарифмические производные цилиндрических функций по аргументам ^ = kR , Z p = ^ ( 1 - p Q / to ) .

Ввиду комплексности функций Ханкеля решения уравнения (3) – спектральные зависимости p = F (to, £), описывают циркуляционные волны с p = p ' + ip ", p " > 0, затухающие из-за излучения

ними индексами: 1 – для неподвижного пьезоэлектрика, 2 – для вращающегося цилиндра ( Г <  R ).

Без временной экспоненты exp(- i to t ), где to — частота волн, решение уравнений (1), описывающее циркуляционную – распространяющуюся

в окружающую цилиндр среду и, поэтому, не представляющие интереса. Снижения затухания можно добиться при условии p ' >  ^ » 1, что вместе с обычным требованием Q ^ to обеспечивает малость значений Z p . С использованием соответствующих асимптотических разложений цилиндрических функций [5] получаем вместо (3) равенство

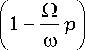
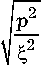
по азимуту щелевую волну, выглядит следующим образом

u1 = Aeip 6 HP1}( kr), u2 = Beip6 Jp (kr), ф. = 4ne u.+eip6r (—1) 1 P|c.

^p j         tu j i er          j , j = 1,2.

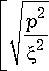
-1

| p|K 2 — 2^

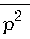
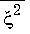
-1

В формулах (2) не целочисленный порядок p цилиндрических функций Бесселя J_p ( x ) и Ханкеля H_p ⁽¹⁾( x ) имеет смысл азимутального волнового числа, k – волновое число сдвиговых волн в материале пьезоэлектриков.

2. Дисперсионное соотношение и результаты

Особенности циркуляционного распространения электрозвуковых волн в круговой щелевой структуре пьезоэлектриков с вращающимся цилиндром можно установить из дисперсионного соотношения. Для его вывода решение (2) следует подставить в граничные условия задачи, выражающие равенство при r = R электрических потенциалов, радиальных компонент электрической индукции, а также, по отдельности, отсутствие сдвигового напряжения на границе цилиндра и на поверхности полости. Из требования разрешимости образующейся системы однородных алгебраических уравнений относительно амплитудных коэффициентов A , B , C _1,2 имеем

При физически обоснованных параметрах правая сторона (4), где K – коэффициент электромеханической связи, отрицательна и решение в форме стационарной циркуляционной волны существует, если линейная скорость вращения точек поверхности цилиндра превышает фазовую скорость циркуляционной волны (to < Q p ). В таком случае происходит эффективная перекачка энергии от вращающегося цилиндра в парциальную волну, распространяющуюся по поверхности полости во внешней среде. Это позволяет компенсировать ее потери на излучение в пьезоэлектрик, окружающий цилиндр, и в целом обеспечивает стационарное распространение циркуляционной щелевой волны. Характерно, что условие to < Q p согласуется с выявленной ранее [4] областью резких резонансных пиков спектра поперечного сечения рассеяния плоской монохроматической волны вращающимся пьезоэлектрическим цилиндром.

Правые стороны уравнений (3), (4) являются четными функциями p , тогда как левые их стороны из-за линейной зависимости Z p = ^ ( 1 - p Q / to ) от p этим качеством не обла-

С.Н. МАРЫШЕВ, Н.С. ШЕВЯХОВ

ФВПиРТС, 2016

дают. В силу данного обстоятельства циркуляционные щелевые волны обладают невзаимностью распространения: при обращении распространения ( p → - p ) или изменении направления вращения цилиндра (Ω → -Ω) теряют стационарность распространения. Дисперсионные спектры медленных ( p >ξ) стационарных циркуляционных волн имеют вид монотонно спадающих зависимостей ω = ω( p ).

Работа выполнена по гранту РФФИ в рамках проекта № 14-07-00621 .