Сечения числовой призмы, связанные с полиномами Бесселя

Основой данной работы служит множество чисел, которые структурированы в виде бесконечной числовой призмы. Рассматриваемое множество (числовая призма) - это упорядоченное объединение бесконечного количества непересекающихся числовых треугольников («пачка» треугольников), каждый последующий из которых зависит от предыдущего.

Рассматриваемое множество чисел возникло в задаче нахождения кумулянтов и моментов [1] нового трехпараметрического вероятностного распределения. Само же это авторское распределение, определяемое характеристической функцией f (t) =

о         о Л - m

В    и  в )

ch—t - i—sh—t I m   в  m )

, при ц , в , m ^ R; m >  0, в * 0, i = V- 1

введено в научную терминологию как распределение «типа гиперболического косинуса». В указанном виде оно получено при решении задачи характеризации распределений условием постоянства регрессии квадратичной статистики на линейную статистику [2, 3]. Найденное распределение исследовано [4, 5] и является обобщением двухпараметрического вероятностного распре деления, известного в литературе [6], как распределение Майкснера (m = в , = 9), которое, в свою очередь, при ц = 0 , m = 1 также обобщает классическое однопараметрическое распределение гиперболического косинуса (секанса).

В [1] установлено, что кумулянты и моменты распределения типа гиперболического косинуса выражаются через семейство полиномов, коэффициенты которых удовлетворяют рекуррентным соотношениям

U (0;0,0) = 1, U (0; k , j ) = 0 для любых k , j * 0,

U ( n + 1; k , j ) = U ( n ; k - 1, j - 1) + ( j - 1) U ( n ; k , j - 1) + ( j + 1) U ( n ; k , j + 1) (1) при n = 0,1,2,...; j , k = 1,2,....

Именно это трехмерное целочисленное множество {U(n; k, j)}, формируемое согласно (1), и классифицируется как числовая призма. При фиксировании одного из аргументов этой призмы получаем распределения соответствующих чисел в одной плоскости, т.е. сечения призмы. Следуя традиции, полученные множества будем называть числовыми треугольниками. В [7] указано, что при фиксировании аргумента k соответствующие сечения содержат упорядоченные коэффициен- ты в разложениях степеней тангенса. Ранее для них найдены дифференциальные соотношения полиномов с этими коэффициентами. При фиксировании двух аргументов множества {U(n; k, j)} приходим к одномерному случаю размещения (упорядочивания) чисел: получается числовая последовательность.

Из числовой призмы числовые последовательности можно получить различным образом. В частности, в [1, 7] представлены некоторые как ранее известные (тангенциальные числа { U (2 n ;1,0)}, обобщенные тангенциальные числа { U ( n ;1, n - 4)}, секансные числа

^ U (2 n ; к ,0)

. к = 1

> и др.), так и новые последовательности. Например, (см. [7], теорема 1) сечение числовой призмы {U(n; к, n)} является числовым треугольником Стирлинга, представляющим совокупность известных целочисленных последовательностей чисел Стирлинга первого рода

{ U ( n ; к , n )} =

n k

, где n , к = 0,1,2,.

а сечение вида { U (2 n + 1; к ,3)} в подавляющем большинстве состоит из неизвестных ранее последовательностей.

Одним из сечений числовой призмы является и числовой треугольник Бесселя. К функциям и полиномам Бесселя, давно ставших математической классикой, не иссякает интерес как к объекту изучения до настоящего времени (см., например, [8]). Изучение полиномов Бесселя, как правило, базируется на дифференциальных и интегральных соотношениях или свойствах и интерпретациях коэффициентов. Отличительной характеристикой данной работы является рассмотрение множества коэффициентов полиномов Бесселя в связи со структурой и соотношениями в числовой призме. Эта связь коэффициентов полиномов и элементов призмы позволяет по-новому, с других позиций изучать как свойства полиномов, так и свойства числовой призмы.

Основная часть

Рассмотрим группу последовательностей: коэффициенты при разложении функций вида P m ( x ) / -J (1 - 2 x )^{2 5 + 1} , где P m ( x ) - полиномы, показатели степени m , s - целые, неотрицательные. Некоторые из такого рода последовательностей приведены в электронной Энциклопедии целочисленных последовательностей ( OEIS) [9]. Представим разложения для этих функций и их место в структуре числовой призмы, см. табл. 1.

Данные разложения замечательны тем, что они представляют коэффициенты в полиномах Бесселя. Согласно заданным в числовой призме последовательностям легко построить известный числовой треугольник Бесселя. Указанные в табл. 1 последовательности располагаются в треугольнике Бесселя по столбцам и являются 1-м, 2-м, 3-м и т.д. коэффициентами в полиномах Бесселя. Коэффициенты полинома Бесселя n -го порядка размещаются в соответствующей n -й строке числового треугольника. Сам треугольник Бесселя входит в рассматриваемую числовую призму как сечение { U (2 n - j ; n , j )}, где n = 0,1,2,..., j = 0,1,2,..., n . Начальные значения треугольника коэффициентов и их место в структуре числовой призмы см. в табл. 2.

Исходя из места коэффициентов в числовой призме, можно выписать полиномы Бесселя в общем виде, опираясь на эту структуру.

Отметим, что полиномами Бесселя называют [10] полиномы yn (x), удовлетворяющие дифференциальному уравнению x2y‘ + (2x + 2)y' - n(n +1)y = 0, n = 0,1,2,..., а также родственные им полиномы [11] pn (x) = xn • yn-11 — |, определяемые при n > 1 и удовле-V x )

творяющие рекуррентному дифференциальному соотношению

P n ( x ) - 2 р П ( x ) + 2 n P n - 1 ( x ) = 0, n = 2,3,4,....

В явном виде соответствующие формулы для y n ( x ) и p n ( x ) такие:

У п ( x ) =

у ( п + k )!   x k

^2 k k !( п - к )!

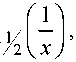
где K_n ( x ) - модифицированная функция Бесселя второго рода;

Р п ( x ) = Y ._v - n k „ „ x k = (2 п - 3)!! x 1 F 1 (1 - п ;2 - 2 п ;2 x ),             (3)

к = 1 2   ( п - к )!( к - 1)!

где 1 F 1 (a ; b ; z ) - гипергеометрическая функция первого рода, п = 2,3,4,....

Таблица 1

Разложения функций вида P m ( x ) / -7(1 - 2 x )^{2 5 + 1}

Функция, f ( x )	Коэффициенты, f ( k ) (0) № в OEIS	Последовательность в призме
1 /( 1 - 2 x )	1,1,3,15,105,945,10395, . [ OEIS : A 001147]	U (2 п ; п , 0), п = 0,1,2,.; U (2 п -1; п , 1), п = 1,2,3,.
1 + x ■\j (1 - 2 X )5	1,6,45,420,4725,62370,945945, . [ OEIS : A 001879]	U (2 п -2; п , 2), п = 2,3,4,.
1 + 3 x 7( 1 - 2 x )7	1,10,105,1260,17325,270270,4729725, . [ OEIS : A 000457]	U (2 п -3; п , 3), п = 3,4,5,.
, , 3 2 1 + 6 x + — x 2 7 (1 - 2 x )9	1,15,210,3150,51975,945945, . [ OEIS : A 001880]	U (2 п -4; п , 4), п = 4,5,6,.
1 + 10 x + — x x 2_ A (1 - 2 x )n	1,21,378,6930,135135,2837835, . [ OEIS : A 001881]	U (2 п -5; п , 5), п = 5,6,7,.
1 + 15 x + 45 x 2 + 5 x 3 2 _ 2 7 (1 - 2 x )13	1,28,630,13860,315315,7567560, . [ OEIS : A 038121]	U (2 п -6; п , 6), п = 6,7,8,.
, ,. 105 2 33 3 1 + 21 x + x + x 2 _ 2 7 (1 - 2 x )15	1,36,990,25740,675675,18378360, ^ [ OEIS : A 130563]	U (2 п -7; п , 7), п = 7,8,9,.
1 + 28 x + 105 x 2 + 70 x 3 + 35 x 4 ____________           _ 8 7 (1 - 2 x )17	1,45,1485,45045,1351350,41351310, ... [отсутствует в OEIS]	U (2 п -8; п , 8), п = 8,9,10,.
1 + 36 x + 189 x 2 + 210 x 3 + 314 x 4 __________ _ 8 7 (1 - 2 x )19	1,55,2145,75075,2552550,87297210, ... [отсутствует в OEIS]	U (2 п -9; п , 9), п = 9,10,11,.
1 + 45 x + 315 x 2 + 525 x 3 + 1575 x 4 + 63 x 5 __________________ _ 8        8 7 (1 - 2 x )21	1,66,3003,120120,4594590,174594420,. [отсутствует в OEIS]	U (2 п -10; п , 10), п = 10,11,12,.

Таблица 2

n j	0	1	2	3	4	5	6	7	8	9
	U (2 n ; n ,0)	U (2 n -1; n ,1)	U (2 n -2; n ,2)	U (2 n -3 n ,3)	U (2 n -4; n ,4)	U (2 n -5; n ,5)	U (2 n -6; n ,6)	U (2 n -7; n ,7)	U (2 n -8; n ,8)	U (2 n -9; n ,9)
0	U (0; 0,0)= 1
1	U (2; 1,0)= 1	U (1; 1,1)= 1
2	U (4; 2,0)= 3	U (3; 2,1)= 3	U (2; 2,2)= 1
3	U (6; 3,0)= 15	U (5; 3,1)= 15	U (4; 3,2)= 6	U (3; 3,3)= 1
4	U (8; 4,0)= 105	U (7; 4,1)= 105	U (6; 4,2)= 45	U (5; 4,3)= 10	U (4; 4,4)= 1
5	U (10; 5,0)= 945	U (9; 5,1)= 945	U (8; 5,2)= 420	U (7; 5,3)= 105	U (6; 5,4)= 15	U (5; 5,5)= 1
6	U (12; 6,0)= 10395	U (11; 6,1)= 10395	U (10; 6,2)= 4725	U (9; 6,3)= 1260	U (8; 6,4)= 210	U (7; 6,5)= 21	U (6; 6,6)= 1
7	U (14; 7,0)= 135135	U (13; 7,1)= 135135	U (12; 7,2)= 6237	U (11; 7,3)= 17325	U (10; 7,4)= 3150	U (9; 7,5)= 378	U (8; 7,6)= 28	U (7; 7,7)= 1
8	U (16; 8,0)= 2027025	U (15; 8,1)= 2027025	U (14; 8,2)= 945945	U (13; 8,3)= 270270	U (12; 8,4)= 51975	U (11; 8,5)= 6930	U (10; 8,6)= 630	U (9; 8,7)= 36	U (8; 8,8)= 1
9	U (18; 9,0)= 34459425	U (17; 9,1)= 34459425	U (16; 9,2)= 16216200	U (15; 9,3)= 4729725	U (14; 9,4)= 945945	U (13; 9,5)= 135135	U (12; 9,6)= 13860	U (11; 9,7)= 990	U (10; 9,8)= 45	U (9; 9,9)= 1

Сечение числовой призмы {U (2 n — j ; n , j )} (числовой треугольник Бесселя)

В частности, известную [OEIS: A001498] модифицированную сферическую функцию Бесселя второго рода kn (x), где kn (x) =

, можно представить в виде

J — K _v( x ) \ nx ^{n +}/7

e — x kn (x ) = ^I pn+1( x)• xn

При этом,

У 0 ^{( x} ) = 1, y 1 ( x ) = x + 1, y ₂( x ) = 3 x ² + 3 x + 1, y ₃ ( x ) = 15 x ³ + 15 x ² + 6 x + 1, y ₄ ( x ) = 105 x ⁴ + 105 x ³ + 45 x ² + 10 x + 1,

P1( x) = x , p 2 (x) = x + x 2, p 3 (x) = 3 x + 3 x 2 + x3, p 4 (x) = 15 x +15 x 2 + 6 x3 + x4, p 5 (x) = 105x +105x2 + 45x3 +10x4 + x5,

Оформим найденные соотношения связи полиномов Бесселя с числовой призмой в виде утверждений.

Теорема 1. Полиномы вида n—1                                                                  n pn(x) = £u(2n — 2 — j;n — 1, j)xj+1 при n > 1; yn(x) = £U(2n — j;n, j)xn—j при n > 0, J'=0                                                                 j=0

где U ( n ; k , j ) - элементы числовой призмы, определяемые (1), являются соответствующими полиномами Бесселя p_n ( x ) и y_n ( x ).

При этом, согласно (3), (2), оказывается, что n-1

P n ( x ) = E U (2 n - 2 - j ; n - 1, j ) x^{j + 1} = (2 n - 3)!! x 1 ^ 1 (1 - n ;2 - 2 n ;2 x ), n = 2,3,4,... (4) j = o

1        (1A yn(x)=EU(2n-j;n,j)x j =J —exK-n-v[_I.                    (5)

j = 0                                 -"- /2 v x )

В соотношении (4) полагая x равными конкретным значениям (в частности, x = 1, x = - 1, x = 2), приходим к равенствам для сумм элементов числовой призмы с использованием значений гипергеометрической функции первого рода 1 F 1 (a ; b ; z )

Теорема 2. Для последовательностей числовой призмы {U(n; k, j)} при n > 2 справедливы соотношения n -1

E U (2 n - 2 - j ; n - 1, j ) = (2 n - 3)!! 1 F(1 - n ;2 - 2 n ;2);

j = 0

n - 1

E ( - 1) j U (2 n - 2 - j ; n - 1, j ) = (2 n - 3)!! 1 F (1 - n ;2 - 2 n ; - 2);

j = 0

n - 1

E U (2 n - 2 - j ; n - 1, j )2 ^j = (2 n - 3)!! 1 F 1 (1 - n ;2 - 2 n ;4). j = o

При x = 1, x = 2 , x = 0,5 из соотношения (5) также следует связь элементов числовой призмы со значениями модифицированной функции Бесселя второго рода K_n ( x ).

Теорема 3. Для последовательностей числовой призмы { U ( n ; k , j )} при n >  0 справедливы соотношения

E и ⁽² n ^{- j} ; n , ^j ) =. — e K__n _ 1/⁽¹⁾;

j = 0                  \^{n   -} n - ^/2

n

EU (2 n - j; n, j )2 n - j = -K_„[-1

j = 0                      V n n /2 V 2 )

n               ( 1 An -j

E U(2n - j; n, j) [ - I   = 4ee2 K_„ jT0           V2) n n

Приравнивая полиномы Бесселя p_n ( x ) и y_n ( x ), представленные в общеизвестном виде (3), (2) и в смысле теоремы 1, приходим к равенству коэффициентов полиномов при одинаковых степенях переменной.

Теорема 4. Для элементов числовой призмы { U ( n ; k , j )} справедливы соотношения

U ⁽² n ^{- 2 - j} ; n ^{- 1, j} ) =       n ,^{2 j )!} , при n > 1, ⁰ ^ ^j ^ n ^- 1;

2 n - j - 1 j !( n - j - 1)!

( n + j )!              „ „

U ( n + j ; n , n - j ) = —:--------- при n >  0, 0 <  j <  n .

2 j j !( n - j )!

Следовательно, элементы числовой призмы в рассматриваемых последовательностях можно выразить через отношение факториалов и степеней, связанных с индексными переменными.

Заключение

Множество { U ( n ; k , j )}, структурированное как числовая призма, заданное соотношениями (1), представляет большое разнообразие упорядоченных подмножеств с различными свойствами. Кроме ряда широко известных целочисленных последовательностей, частично представленных в [1, 7], в данной работе выделены последовательности, связанные с полиномами Бесселя, указаны их свойства именно, как объектов числовой призмы, представлены некоторые соотношения.

Отметим, что множество { U ( n ; k , j )}, обладая элементарностью построения своих элементов, содержит объекты более сложной структуры, связанные с функциональными преобразованиями, дифференцированием и интегрированием функций. Изучение этого множества позволяет выявить неизвестные ранее свойства и связи как уже известных математических объектов (конкретных последовательностей, полиномов, функций и др.), так и находить новые с последующими приложениями. В частности, в [7] указываются взаимно-обратные соотношения между секанс-ными числами { E j } = {1,1,5,61,1385,50521,2702765,...} и тангенциальными числами { T j } = {1,2,16,272,7936,353792,...}, j = 1,2,...; также в последовательности чередующихся се-кансных и тангенциальных чисел (1, 1, 1, 2, 5, 16, 61, 272, 1385, 7936, …) найдены формулы связи, выражающие элементы последовательности через свои предыдущие. В [12] представлено множество нетривиальных интегралов от комбинаций некоторых функций (показательной, степенной, гиперболических косинуса или синуса и определенного вида полиномов-сомножителей), вычисляемых с помощью свойств { U ( n ; k , j )}. Указан ряд конкретных соотношений.

Безусловно, дальнейшее изучение структуры и свойств представленного числового множества { U ( n ; k , j )} является перспективным в теоретическом и прикладном аспектах.

Работа выполнена при финансовой поддержке проектной части государственного задания в сфере научной активности Министерства образования и науки Российской Федерации, проект № 1.949.2014/K.