Седиментация малоконцентрированной полидисперсной взвеси стоксовских частиц в плоском слое

Введение. Процесс осаждения малоконцентрированной полидисперсной взвеси находит широкое использование в энергетике, химической и пищевой технологиях [1, 2], а если при этом несущая среда является условно неподвижной, то этот процесс имеет фундаментальное значение в седиментометрическом анализе дисперсной фазы [3]. В частности, если скорость частиц постоянна, что означает уравновешивание силы тяжести силами гидродинамического сопротивления, то такие частицы принято называть стоксовскими [4]. Анализ процесса осаждения с позиций механики гетерогенных сред вызывает ряд трудностей, связанных с идентификацией межфазной границы [5], что, в конечном счете, делает невозможным постановку краевых условий и применение интегро-дифференциального исчисления. Альтернативой этому является применение диффузионно-кинетической модели процесса осаждения [6], что с успехом апробировано при решении ряда задач [7, 8].

Постановка задачи. Рассмотрим плоский слой дисперсионной среды высотой h со свободной поверхностью, которая содержит равномерно распределенную дисперсную фазу малоконцентрированных полидисперсных частиц. Направим ось Ox декартовой координаты с началом на поверхности осаждения перпендикулярно к свободной поверхности, тогда диффузионнокинетическая модель осаждения монодисперсной взвеси имеет вид [9]:

д n ( x , т )      д n ( x , т ) ^d ² n ( x , т )

—= w— + D --;                   (1)

д т	д x          д x 2 n ( x ,0 ) = n 0 ;                                            (2)

(w - k) n (0,т) + D д n(0,T) = 0;(3)

дx wn(h,т) + D дn(h,т) = 0,(4)

дx где т, x - время и декартова координата; n (x,т) - локальная счетная концентрация частиц размера l; w – стоксовская скорость осаждения частиц размера l; D – коэффициент конвективного перемешивания взвеси; k – кинетический коэффициент встраивания частиц в структуру осадка.

Если перемешивание отсутствует ( D = 0 ) , то из (3) следует, что k ^ w , т. е. частицы, подошедшие к поверхности осаждения, беспрепятственно оказываются в осадке. Поэтому (1)–(4)

трансформируется в систему: дn(x ,т)     дn(x ,т) = w,                                     (5) дт         дx                                         ’ n (x ,т ) = n 0,                                               (6) n (0,т)^ n 0,                                               (7) n (h ,т) = 0.                                            (8) Из (5)–(8) следует, что n (0,т) = [Н(т)-Н(т - h/w)] n 0, где Н(...) - функция Хэвисайда. В силу малоконцентрированности взвеси система (5)-(8) может быть обобщена на полидисперсный случай, используя принцип суперпозиции концентрационных полей, т. е. дf(x, l,т) = w (l )дf(x, l,т)                                        (9) дт            дx f (x,l,0) = f0(l),                                            (10) f (0, l ,т) = {н(т)-Н [т - h/w(l)]} f0(l),                            (11) где f0 (l), f (x, l,т) - исходная и локальная счетные функции плотности распределения частиц по размерам.

В безразмерном виде система (9)–(11) такова:

дF(X,L,0) _ 2 дF(X,L,0),„ „ д9             дX    ’

F(X,L,0) = Fo(L);(13)

F(0,L,0) = [Н(0)-Н(0-L2)]F0(L),(14)

где 0 = w ( l ) т/ h ;      X = x/h ;      L = l/l ;      F ( X , L , 0 ) = lf ⁽ N ) ( x , l , т ) ;      F₀ ( L ) = lf ⁽ N ) ( l ) ;

max j f 0 (l) dl;

l min

lmax

f ⁽ N ) ( l )= f 0 ( l )/ J f 0 ( l ) dl ; T = j f ⁽ N ) ( l ) dl ;

min , max

lmin минимальный и максимальный размеры частиц взвеси.

Применяя одностороннее преобразование Лапласа по 0 , получим решение (12)-(14)

F(X,L,0) = {н(0)-Н[0-(1 -X)L"2]}F0 (L).(15)

С помощью (15) определены: локальная относительная массовая концентрация частиц во взвеси

Ряжских В.И.,                  Седиментация малоконцентрированной полидисперсной взвеси

Ряжских А.В.                                            стоксовских частиц в плоском слое

Lmax

C(X,e) = c+x?’ = J LF(X,L,e)dL   J F0 (L)dL,(16)

Lmin lmax где Lmin = lmin Г , Lmax = lmax^ , c(x,T’ = kVPt J l3f(x,l,T’dl , c0 = kVPt J l3f0 (l’dl , lmin kV - коэффициент формы частиц, pT - плотность частиц; среднеобъемная относительная массо- вая концентрация частиц

C ( e ) = J C ( X, e ) dX ;

l max

3(т ) = -k^T w (l) l3 1 - £ lmin

т

J f (0, l ,£) d^

dl ; S ₀ =

kV

1 - £

lmax h J l3 f0 (l) dl lmin

; £ - порозность осадка взвеси.

относительная толщина осадка »(e )=^<1’=Lmax L’ O0 min e [JF<0'L '#)d5\ dLj Lmax / J L3 F0 (L) dL, Lmin (18) где

Пример расчета. В практике наиболее часто встречается экспоненциальный закон распределения взвеси, например, в процессах кристаллизации твердой фазы из растворов, объемной конденсации парообразных сред и т. д. В этом случае F0 (L ) = exp (-L) и приближенно можно считать Lmin = 0, Lmax ^ ~. Заметим, что условие нормировки при этом выполняется автоматически. Тогда из (15) следует

F (X, L ,e) = {H(e)-H[e-(1 - X) L-2 ]}exp(-L).

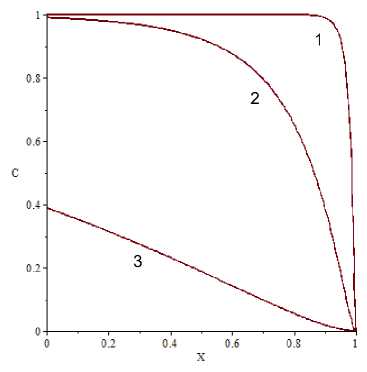
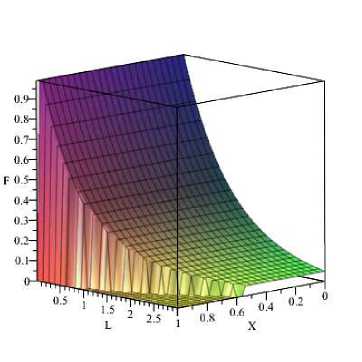
Рис. 1. Безразмерная функция плотности распределе-   Рис. 2. Относительная массовая концентрация частиц ния частиц по размеру при e = 0,05                  при: 1 — e = 0,001; 2 - e = 0,01; 3 - e = 0,1

Трансформирование F ( X , L, e ) в процессе седиментации показано на рис. 1. Выражение для локальной относительной массовой концентрации частиц во взвеси (16) принимает вид (рис. 2)

C ( X , е ) = [ б - ⁽ L *3 + 3 L *³ + 6 L * + 6 ) exp ( - L *) ] /б,

где L = ^( 1 - X )/ e . Кинетика осветления взвеси в процессе осаждения есть

с (е )=2 [б0е - з-(60e+ve+60/ Ve+27+7/ 7ё) exp (-V Тё)] .

Относительная толщина осадка представлена в квадратурах

_ e

ale ) = J[120 (< '3 + 5^-2 + 20^3/2 + 60< 1 +120^^1 +120)exp(-0,5/^)]d^ .

В частности, если известна экспериментальная относительная седиментационная кривая о э ( т ) , то решив оптимизационную задачу

11 - окат)/оэ (т)| ^ min,

а в которой а = w(l)/h, нетрудно найти

l =

18 pva у g ^{( р} т ^{- p} )

где р - плотность; v - кинематическая

вязкость несущей среды; g – ускорение свободного падения.

Заключение. Аналитический анализ позволил получить основные характеристики кинетики осаждения малоконцентрированной полидисперсной взвеси стоксовских частиц в неподвижной несущей среде инвариантно физико-химическим свойствам гетерогенной системы и на его основе предложить способ идентификации среднего размера взвеси по экспериментальной седиментационной кривой.