Сегментация 3D моделей данных с помощью мультимодального динамического графа CNN

При дешифрировании археологических памятников исследователи часто используют методы классификации и сегментации 3D данных на основе различных архитектур сверточных нейронных сетей. Методы можно поделить на непрямые, например, мультивидовые сверточный нейронные сети (MVCNN, multi-view convolutional neural network) [1] и прямые: PointNet [2], PointNet++ [3], на основе графа сверточной нейронной сети (GCNN, Graph Convolutional Neural Networks) [4]. На основе GCNN разработаны различные модификации: на основе динамического графа сверточной нейронной сети (DGCNN, dynamic graph CNN) [5], регулярного графа сверточной нейронной сети (RGСNN, regularized graph CNN) [6], ConvPoint [7]. Применение непрямых методов ограниченно, так как они обеспечивают хорошее качество семантической обработки только для простых полигональных моделей 3D данных, непрямые методы имеют низкую производительность и часто требовательны к памяти для хранения результатов. PointNet и PointNet++ основаны на локальной обработке точек, не используют геометрические отношения между точками и инвариантны к перестановкам, данные методы находят широкое применение в промышленном дизайне. Модификации прямых методов на основе GCNN при семантической обработке 3D данных используют информацию о форме и поверхности объекта, процесс классификации и сегментации в них основан на выполнении множественных операций фильтрации и свертки сигналов на пространственных динамических графах в спектральной области. Например, в методе на основе RGGNN для описания связности компонент пространственного графа используется матрица Кирхгофа, построение которой имеет большую вычислительную сложность O n3 , что ограничивает применение метода при анализе крупномасштабных 3D сцен. GCNN и DGCNN плохо работают с локальными признаками объектов и находят основное применение при семантической классификации 3D объектов. Главный недостаток DGCNN и RGCNN связан с размерностью анализируемых облаков точек: методы сегментации на основе этих сетей хорошо подходят для семантической обработки эталонных коллекций 3D объектов, но плохо применимы к обработке реальных данных в виде плотных крупномасштабных облаков точек. Точность процедуры сегментации на основе различных модификаций GCNN зависит от формы объекта и способа формирования облака точек: хорошо сегментируются только исходные или идеально выровненные облака точек.

В последнее время был предложен ряд эффективных архитектур нейронных сетей для решения задачи классификации и семантической сегментации 3D данных, таких как, ConvPoint [7], KPConv [8], ShellNet [9] и Superpoint Transformer [10]. В табл. 1 представлены количественные результаты, которые иллюстрируют современное состояние методов для решения задачи 3D семантической сегментации с использованием коллекции данных Dales (A Large-scale Aerial LiDAR Data Set for Semantic Segmentation) [11]. В исследовании [7] предложен оригинальный метод, который использует непрерывные свертки при обработке облаков точек с неструктурированной природой и оказывается более эффективным, чем классические методы для 3D семантической сегментации [4–6]. ConvPoint в отличии от других методов способен работать с крупномасштабными наборами данных, которые могут включать тысячи плотных облаков точек большой размерности. Данная особенность и хорошие показатели качества по метрикам общей точности (OA, Overall Accuracy) и среднего пересечения над объединением (mIoU, mean intersection over union) делают данный метод кандидатом для решения поставленной в работе задачи по 3D семантической сегментации археологических памятников бронзового века. В исследовании [8] представлен новый подход к свертке точек KPConv для обработки облаков точек, который отличается деформируемой операцией свертки. Предложенный метод хорошо адаптируется к локальной геометрии облака точек и эффективен для обработки облаков точек различной плотности. KPConv был апробирован на многих наборах данных, кроме Dales, и для всех коллекций показывает хорошие показатели в терминах метрик OA и mIoU.

Методы PointNet и PointNet++ были одними из первых методов для 3D семантической сегментации, тем не менее они по-прежнему занимают высокие места в рейтинге качества, а для многих коллекций данных они показывают наилучшие результаты. В методе PointNet++ используется нейронная сеть с иерархической структурой для обработки наборов точек в метрическом пространстве. Данный метод использует метрику расстояния базового пространства и эффективно фиксирует локальные объекты в нескольких масштабах. PointNet++ показывает выдающиеся результаты для наборов данных с неоднородной плотностью выборки, а также отличается высокой производительностью.

В исследовании [9] предложена эффективная сверточная нейронная сеть ShellNet, использующая статистические данные из концентрических сферических оболочек для определения репрезентативных признаков в облаке точек при вычислении свертки. Предложенный подход позволяет с одной стороны существенно увеличить скорость обучения нейронной сети, а с другой стороны позволяет достигать самых современных результатов при классификации 3D объектов, сегментации частей объектов и семантической сегментации 3D сцен. Архитектура ShellNet подчеркивает потенциал оптимизированных нейронных сетей в обработке контекстуально сложных и крупномасштабных 3D сцен.

В исследовании Superpoint Transformer [10] представлен новый подход для эффективной семантической сегментации крупномасштабных 3D сцен на основе архитектуры трансформера. В архитектуре используется быстрый алгоритм для разбиения облаков точек на иерархические структуры суперпунктов, что позволяет значительно ускорить процедуру предварительной обработки 3D данных. В Superpoint Transformer используется разреженный механизм самовнимания для понимания взаимосвязей между суперпунктами в нескольких масштабах. Superpoint Transformer показывает высокое качество 3D семантической сегментации на тестовых наборах данных, обладает высокой производительностью, позволяет в компактной форме хранить модели в памяти.

Таблица 1. Результаты 3D семантической сегментации на коллекции данных Dales

Рейтинг	Модель	mIoU	Общая точность	Размер модели	Год
1	KPConv	81.1	97.8	14.1M	2019
2	Superpoint Transformer	79.6	97.5	212K	2023
3	SuperCluster	77.3	97.2	210M	2024
4	PointNet++	68.3	95.7	3.0M	2017
5	ConvPoint	67.4	97.2	4.7M	2018
6	SPG	60.6	95.5	280K	2018
7	PointCNN	58.4	97.2	N/A	2018
8	ShellNet	57.4	96.4	N/A	2019

Данная статья посвящена решению задачи повышения точности методов 3D сегментации облаков точек, в ней предложен метод сегментации на основе мультимодального динамического взвешенного графа DGCNN*, который использует лучшие идеи DGCNN и RGCNN, но свободен от ряда их ключевых недостатков. В этой статье мы исследуем методы сегментации, основанные на построении динамического графа CNN, методы на основе архитектуры трансформера не рассматриваются в данной статье.

В разделе 1 представлена архитектура мультимодального динамического граф DGCNN*, а также рассмотрены вопросы предварительной обработки облаков точек и их регистрации при построении 3D c разных углов обзора на сцене. В разделе 2 представлен алгоритм семантической сегментации 3D данных на основе DGCNN*. В разделе 3 представлены результаты компьютерного моделирования при решении задачи исследования структуры археологических данных на примере созданного набора данных, содержащего археологические памятники бронзового века на территории Южного Зауралья. В заключении представлены результаты применения алгоритма сегментации на основе DGCNN* на примере набора данных ModelNet 40, указано направление дальнейших исследований.

• 1.    Мультимодальный динамический граф DGCNN*

  • 1.1.    Определение динамического графа сверточной нейронной сети DGCNN*

Археологические памятники включают в себя множество объектов и артефактов, поэтому метод сегментации должен извлекать как глобальные признаки памятника, так и локальные признаки, которые связаны с конкретными объектами или их частями. Входные данные для DGCNN* представляют плотное нерегулярное облако точек C = { c i ,...,c n } в R ³ , где i = 1,...,n, c = ( с Х ,с У ,c Z ,n X ,п У ,n, R i ,G i , B i ) — вектор признаков точки в виде координат точки (с Х , с У ,c Z ) ^т , нормалей (п Х ,п У ,n Z ) ^т и компонент цвета ( R i , G i , B i ) ^т . Пусть m — число семантических меток L = {l i ,...,l k } в N , где к = 1,...,n , тогда выход сети DGCNN* C = {c S ,..., c S } будет иметь размерность n х m для каждой точки в облаке C . Каналы цветовой модели тон, насыщенность, значение (HSV, hue, saturation, value) обладают различной типологической информацией, поэтому их можно рассматривать как независимые признаки в отличие от каналов цветовой модели красный, зеленый, синий (RGB, red, green, blue). Поэтому в работе признаки RGB преобразованы в HSV. DGCNN* основана на концепции построения динамического графа, формируемого путем пересчета матрицы Кирхгофа графа в каждом сверточном слое сети. DGCNN* принимает плотные облака точек с выбранным набором признаков, анализирует локальные особенности объектов с использованием множественной операции свертки на графах в специальных слоях EdgeConv, и затем с помощью метрического классификатора на базе двух многослойных сетей прямого распространения (MLP, multi-layer perceptron) и одной радиально-базисной сети (RBF, radial basis function) осуществляет сегментацию 3D объектов.

• 1.2.    Регистрация 3D данных

В археологии дешифрирование археологического памятника осуществляется на основе 3D моделей рельефа, полученных с разных точек обзора. Поэтому возникает необходимость решения задачи реконструкции 3D модели памятника. Введем следующие определения: X = {xi, ...,xn} и Y = {yi, ...,ym} — исходное и целевое облако точек в R3. Одним из известных решений задачи является итеративный алгоритм ближайших точек (ICP, iterative closest point). На основе ICP авторами работы разработан точный комбинированный алгоритм регистрации 3D данных (FICP, fusion iterative closest point) [12], в котором решение вариационной задачи представлено как mn

JRVRD W A Е IIM(RVFi) -M W)ll ■ w ,.12 №DX> + T-yj|2’ (1) \mathrm{f} i\inAf                                                                                                                                     \mathrm{d} j\inAd где Fxi , Fyi — особые точки [13]; RV — матрица аффинного преобразования для данных о цветовых признаках кадра; RD и T — матрица поворота и вектор переноса для карты глубины соответственно; M — функция преобразования координат особых точек в систему координат камеры; \alpha,W — весовые коэффициенты; Af — связи между особыми точками; Ad — связи между соответствующими точками xj и yj в облаках. Алгоритм позволяет решить проблему зависимости решения вариационной задачи от правильности выбора начальных значений, используется для точной регистрации облаков точек с произвольным пространственным разрешением и масштабом относительно друг друга.

• 1.3.    Предварительная обработка данных

Большинство 3D датчиков глубины генерируют разреженные, зашумленные и неоднородные облака точек, что оказывает негативное влияние на процесс классификации и сегментации 3D объектов. Поэтому для предобработки в DGCNN* использован алгоритм с контролируемой повышающей дискретизацией облака точек на основе метода k ближайших соседей (kNN), который позволяет получить плотное, полное и однородное облако точек. Функция потерь алгоритма

N 2

L up = E E ^ (ii c j - id 7 (ii c j - c i H ),                          (2)

i =0 j E K(i)

где N 2 — количество точек в облаке, K (i ) — число к соседей для точки C i , ^ ( r ) = r — потеря отталкивания, 7(r) = exp ( -6r ² ) , S — гиперпараметр функции быстрого снижения веса 7 .

• 1.4.    Построение мультимодального динамического графа

Пусть задан неориентированный граф вида G = {P, E, A } , где P — множество вершин, E — множество ребер, A — взвешенная симметричная матрица смежности с элементом ( a i,j ) nxn — вес ребра ( i,j ) , при этом a i,j ^ 0 . Тогда из матрицы A можно получить матрицу Кирхгофа с помощью формулы L _c := D — A , где D — матрица степеней с элементом ( d ij ) n x n = n=j = i ^a ij • Для удаления вершины графа с большим весов в матрице Кирхгофа необходимо выполнить нормализацию компонентов матрицы L C um = I — (D + ) ¹/² A (D + ) ¹/² , где D + — обратная матрица Мура—Пенроуза, I — единичная матрица, при этом изолированные вершины исключаются из процесса нормализации. Для каждой вершины графа G выполняется установка связи с вектором ее признаков C i с характеристиками i -ой точки в облаке, данному вектору с помощью функции s i (сигнал графа) ставится соответствие вида s \rightarrow \BbbR. Для создания мультимодального динамического графа G используется алгоритм: Шаг 1 . Определение связей для каждой точки облака точек c i с другими точками c j в облаке.

Шаг 2. Определение значений веса ребра aij = exp —a ^wi cxyzz — cxyz || + W2 ||nxyz — ny* ||2 + W3 || cig — cjgbH2) , где a — гиперпараметр, управляющий балансом между точностью решения и гладкостью графа, wi, W2, W3 — веса групп признаков.

Шаг 3 . Стоп.

• 1.5.    Фильтрация и свертка графа

Облако точек представляет собой нерегулярный набор данных с неупорядоченными вершинами ci , поэтому возникают проблемы с подбором ядра свертки в области вершин. В работе произведена фильтрация векторов признаков ci в спектральной области с помощью преобразования Фурье графа, а затем применена аппроксимация с помощью многочлена Чебышёва для повышения производительности процедуры фильтрации и свертки графа. Матрица Кирхгофа имеет собственные значения Xi, такие что 0 = Л1 С Л 2 С ••• С Xn, которым соответствуют собственные векторы ^(l) = ^il), ^2l), • • •, ^N)) J- .Собственные векторы образуют ортонормированный базис U = (^^i), ^^2),...,^^N)). Тогда матрица Кирхгофа L = U diag(X)Uт, где diag(X) — диагональная матрица. Прямое преоб- разование Фурье графа определяется по формуле GF[s] (Xi) = s (Xi) = ^Nx

^{s ( i )} (^J ^{l )}) ^T ,

а обратное — по формуле IGF[s](i) = s(i) = ^Ng1 s (Xi) p(i). Пусть спектральный фильтр задан вектором \psi \in \BbbRN , тогда компонента вектора \psii может быть определена как зна-

чение функции g^ : К+ ^ R в i-ом собственном числе ^i = g^ (Xi). Пусть на графе заданы G два сигнала si и S2, тогда, используя свойства преобразования Фурье, получим si * S2 = IGF [GF ([si] • GF ([S2])], где ’ — операция покомпонентного умножения, * — операция свертки. На основе теоремы о свертке функций получим формулы для вычисления свертки двух сигналов на графе

(si * «2>(i) = £ si (Xi) Й (Al) p<’ l=0                                                          (3)

S 2 = g ^ ( L C m ) s i = g ^ ( U diag(X)U ^T ) s i .

Для аппроксимации спектральной фильтрации были использованы многочлены Чебышёва, которые позволяют повысить производительность метода сегментации. Пусть N — число коэффициентов Чебышёва в многочлене, тогда запишем функцию g^ в виде g^ (x) = |xg + ^^=i xmTm(x), Vx G [0, Xjv]. Тогда результат действия n-го многочлена Чебышёва на сигнал si может быть определен по формуле м-i

S 2 = g , ( L ^ss^um ) s i ^ £ ^ m T m ( L SU^m ) s i. m =0

При N = 1 фильтрация с помощью многочлена Чебышёва аналогична работе однослойного персептрона. Известно, что информация о локальных особенностях не теряется при свертке графа с многочленами Чебышёва высокого порядка N >  3 . Нормализованная матрица Кирхгофа L _c ^sum разрежена и операция ее умножения на вектор имеет линейную сложность O( | E | ) . Тогда для первых N степеней многочлена вычислительная сложность операции свертки сигналов s i и s 2 с использованием многочлена Чебышёва равна O ( N | E | ) .

• 1.6.    Функция потерь

• 2.    Алгоритм сегментации 3D данных

Функция потерь Llos имеет два слагаемых и основана на вычислении мультиклассовой кросс-энтропии LCE , также в нее добавлен параметр регуляризации Ls , связанный с гладкостью сигнала графа s, который вычисляется по трем слоям свертки DGCNN*. Данный параметр позволяет делать объекты смежных вершин более похожими, что облегчает задачу семантической сегментации. Пусть Xi — входной вектор сигнала, Yi — целевой вектор сигнала, тогда м             3

L ios ( X i , Y i ) = L ce + L _s = - £ y ij log p ij + a £ fm^L s^{u m} fm k ,

j=i k=i

где M — количество возможных меток класса; y i_,j — бинарный признак (маска класса), P ij — прогнозируемая вероятность модели, которая определяет вероятность того, что (i, j) маска принадлежит классу j ; fm k — карта признаков для k слоя в графе свертки; \alpha — гиперпараметр, в работе используем значение равное 10 ^{- 9} . Предложенная функция потерь L l_os обеспечивает сглаживание Лапласа в пространственной и спектральной областях.

Входными данными алгоритма сегментации на основе DGCNN* является набор данных из 9 элементов для каждой точки: координаты, координаты вектора нормалей и данные о цвете, в процессе работы алгоритма данный набор дополняется нормализованными координатами. Координаты точки позволяют осуществлять глобальное позиционирование точек во всем облаке точек, в то время как нормализованные координаты представляют расположение внутри локального блока данных в облаке точек.

В работе произведена модификация первого сверточного слоя GCNN таким образом, чтобы kNN мог динамически использовать информацию о нормализованных координатах и нормалях векторов при поиске соседей для каждой точки. Далее информация в сети последовательно обрабатывается тремя слоями EdgeConv с коэффициентами Чебышёва, равными 6, 5 и 3 соответственно, двумя слоями MLP и одним слоем c радиально-базисными функциями с максимальным объединением объектов из разных слоев, что позволяет извлекать признаки глобальных и локальных объектов в облаке точек. Каждый слой EdgeConv включает в себя построение мультимодального динамического взвешенного графа, фильтрацию объектов и свертку графа. Эксперименты показали, что для повышения точности сегментации нужно осуществлять пересчет матрицы Кирхгофа графа G для каждого слоя EdgeConv. С помощью слоев EdgeConv и слоя пулинга на выходе нейронной сети получаем исходный набор данных с оценками сегментации для каждого класса. На вход модуля построения графов подаются только нормализованные координаты, а на вход сверточного слоя подаются как исходные, так и нормализованные координаты точек.

Далее представим алгоритм сегментации 3D моделей данных на основе DGCNN*.

procedure DGCNN*

Входные данные: C = { c i , ...,c n }

Выходные данные: C = {c S ,..., c S }

• 1:    Инициализация: Чебышёв {6,5,3}, k =1 (Счетчик Чебышёва);

• 2:    Дискретизация облака точек (UpSampling);

• 3:    Преобразование RGB ^ HSV; Формирование вектора признаков {C i };

• 4:    for k in 1,. . . , 3 do

• 5:    Расчет матрицы Кирхгофа L k ;

• 6:    Нормализация компонентов матрицы L ^sum ;

• 7:    Апроксимация сигнала графа многочленом Чебышёва g \psi со степенью k ;

• 8:    Свертка графа GCNN: s ₂ = g ^ ( L sum' j s i

• 9:    Формирование признаков динамического графа G ;

• 10:    end ;

• 11:    MLP 1 (1024);

• 12:    MLP 2 (512);

• 13:    concatenation (EdgeConv 2, MLP2);

• 14:    Формирование результата сегментации на основе RBF;

• 15:    Вычисление функции потерь L io_s ( X i ,Y i ) (см. (5) ).

• 3.    Компьютерное моделирование

  В работе проведено компьютерное моделирование с использованием эталонного набора ModelNet 40 (табл. 2 и табл. 3) и набора данных, содержащего археологические памятники бронзового века на территории Южного Зауралья [14] , а именно облаков точек, полученных в результате тахеометрической съемки археологического комплекса Синташта (табл. 4 и табл. 5) с использованием тахеометра Trimble 3300. Для компьютерного моделирования на коллекции данных, содержащей археологические памятники бронзового века, для регистрации облаков точек были использованы алгоритмы итеративного алгоритма ближайших точек на основе нормалей (NICP, Normal Iterative Closest Point) и комбинированного итеративного алгоритма ближайших точек (FICP).

На рис. 1 представлена архитектура сверточной нейронной сети на основе регулярного динамического взвешенного графа DGCNN*.

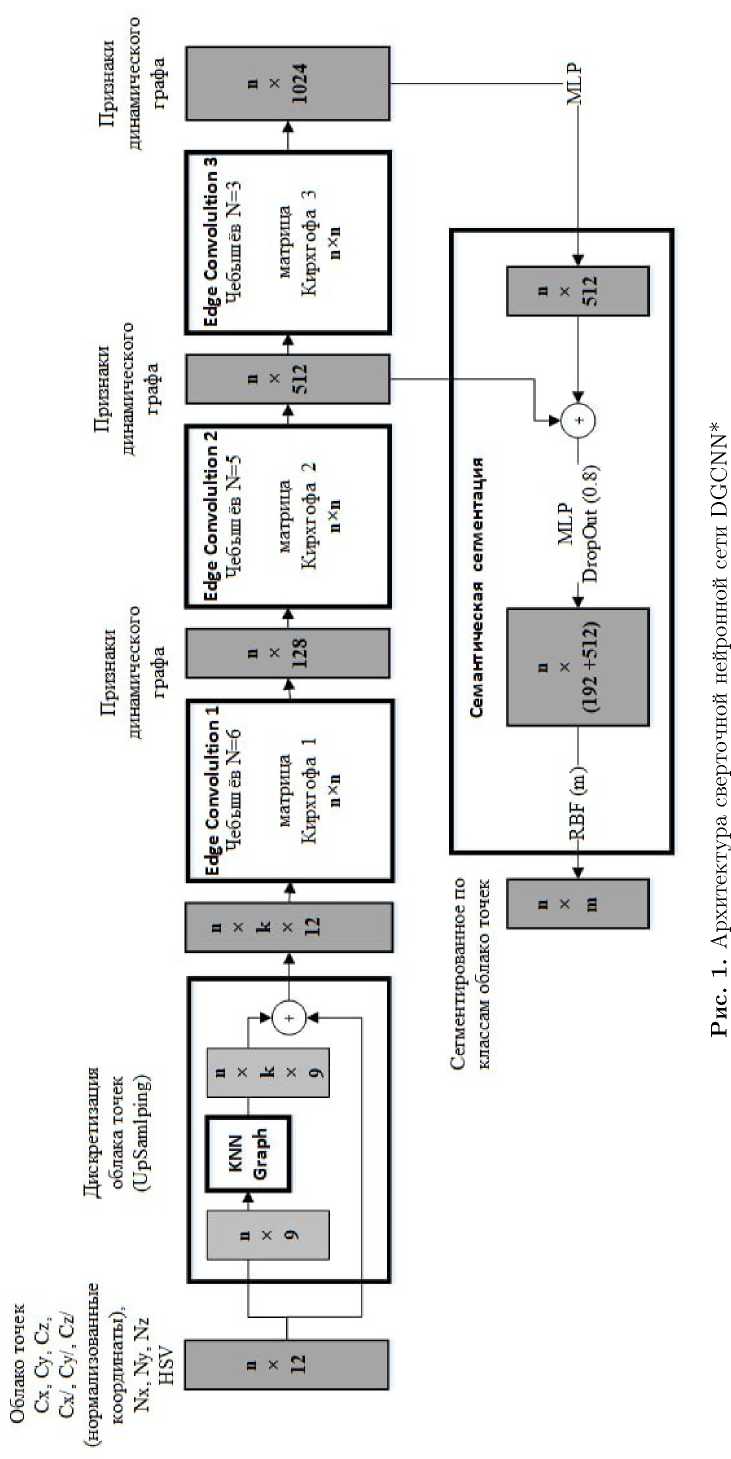
Таблица 2. Точность 3D сегментации для эталонного набора данных ModelNet 40 для исходного облака точек

Наименование метода	Mean Асс Обучающая выборка	Mean Acc Валид. выборка	Mean Асс
			Тестовая выборка	F1- мера
Point Net	0.683	0.533	0.520	0.247
Point Net++	0.734	0.648	0.611	0.412
DGCNN	0.891	0.796	0.744	0.747
DGCNN+RGB	0.902	0.841	0.817	0.821
RGCNN	0.896	0.855	0.819	0.789
ConvPoint	0.916	0.903	0.894	0.833
KPConv	0.941	0.886	0.861	0.866
DGCNN*	0.934	0.923	0.907	0.854

Таблица 3. Точность 3D сегментации для эталонного набора данных

ModelNet 40 для выровненного облака точек

Наименование метода	Mean Асс Обучающая выборка	Mean Acc Валид. выборка	Mean Асс Тестовая выборка	F1-мера
DGCNN* + NICP	0.712	0.686	0.674	0.444
DGCNN* + FICP	0.825	0.798	0.776	0.631

Во втором случае облако точек не содержало данных о цвете, поэтому была проведена его раскраска с использованием системы картографирования Trimble MX9 и соответствующих RGB кадров. Из ModelNet 40 было отобрано четыре набора данных с общим количеством объектов 456. Облака точек, полученные с помощью тахеометрической съемки, содержат от 400 до 1200 точек для каждого археологического бронзового памятника, поэтому требуется увеличение плотности облака точек.

Таблица 4. Точность 3D сегментации по данным тахеометрической съемки для исходного облака точек

Наименование метода	Mean Асс Обучающая выборка	Mean Acс Валид. выборка	Mean Асс
			Тестовая выборка	F1- мера
Point Net	0.623	0.476	0.471	0.256
Point Net++	0.655	0.644	0.602	0.398
DGCNN	0.792	0.713	0.688	0.646
DGCNN+RGB	0.776	0.708	0.653	0.629
ConvPoint	0.833	0.8	0.711	0.625
KPConv	0.796	0.746	0.735	0.634
RGCNN	0.814	0.776	0.72	0.725
DGCNN*	0.862	0.791	0.773	0.622

Таблица 5. Точность 3D сегментации по данным тахеометрической съемки для выровненного облака точек

Наименование метода	Mean Асс Обучающая выборка	Mean Асс Валид. выборка	Mean Acc Тестовая выборка	F1- мера
DGCNN* + NICP	0.69	0.543	0.511	0.475
DGCNN* + FICP	0.786	0.742	0.753	0.685

Далее представим псевдокод модифицированного иерархического алгоритма агломе-ративной кластеризации.

procedure GLA*

Входные данные: max distance = 0.3, P IN = {p IN , -.pp InN }

Выходные данные: P OUT = {p OUT , ...,p mU^T }

• 1:    points norm = Нормализация точек P IN в интервале [0...1] ;

• 2:    model cluster = new Agglomerative Clustering (max distance);

• 3:    model ciu_ster = Обучение нейронной сети (points _norm );

• 4:    Clusters = { ci, ■■■,c _n } = model ci_uster . Получить кластеры (points norm ) ;

• 5:    for Кластер j in model _cl_ust_er .Кластеры() do

• 6:      points ci_uster = Фильтрация (points norm , Кластер j );

• 7:      if points ciuster .Счетчик точек() <  p aug then // p aug = 4 , параметр кластеризации

• 8:          P ^OUT .Добавление точек( points _cl_uster );

• 9:          continue;

  10:

  11:

  12:

  13:

  
  

  end ;

  
  

Grid points = Создать сетку точек (Крайние точки. points ciuster );

points interpolation — Интерполяция (points ciuster , Grid points );

POU . ( points interpolation)' ,

• 14:    end ;

• 15:    Формирование результата агломеративной кластеризации.

Для увеличения плотности облака точек и повышения степени равномерности точек в облаке в работе были использованы модифицированный иерархический алгоритм аг-ломеративной кластеризации Agglomerative Clustering, а точнее вариант на основе GLA* (Generic_linkage algorithm) [15] и алгоритм повышающей дискретизации облаков точек на основе графовой сверточной нейронной сети (PU-GCN, point cloud upsampling using graph convolutional networks) [16] .

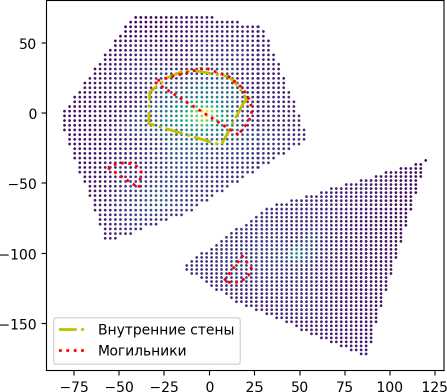
На рис. 2 представлены результаты работы алгоритма GLA* для могильника вблизи п. Осиповка.

h 259.5

- 259.0

- 258.5

- 260.0

Рис. 2. Результаты повышения размерности облака точек с использованием алгоритма GLA* на примере могильника вблизи п. Осиповка: а) облако точек до применения алгоритма агломеративной кластеризации b) облако точек после применения алгоритма агломеративной кластеризации

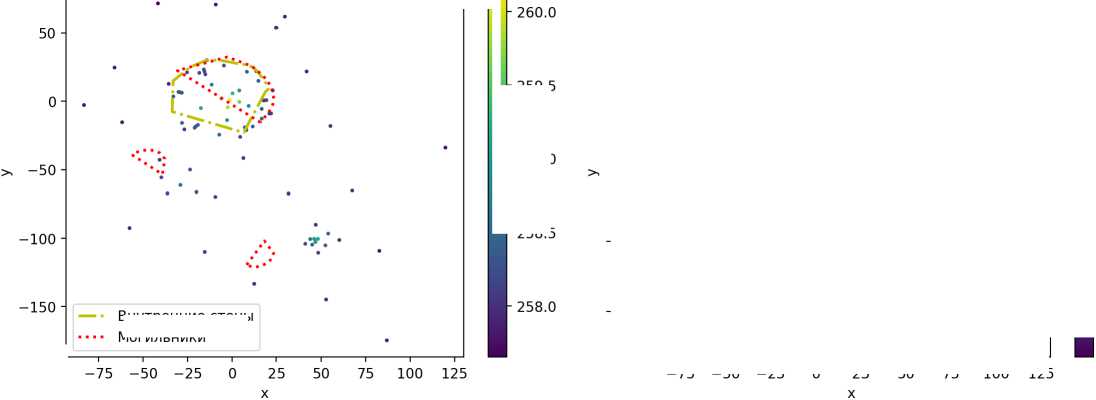
Внутренние стены Могильники

- 259.5

- 259.0

- 258.5

- 258.0

(b)

(a)

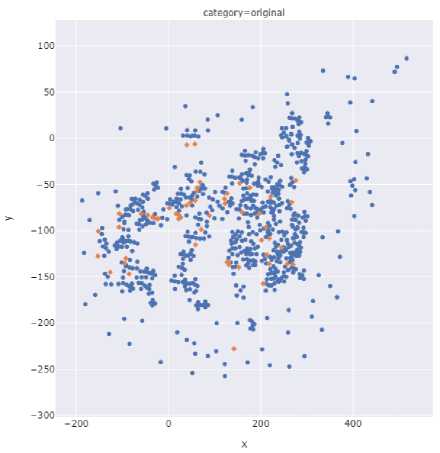
На рис. 3 представлены результаты работы алгоритма повышающей дискретизации облаков точек PU-GCN на примере археологического памятника бронзового века вблизи п. Каменка Челябинской области.

Построенные модели обучены на ПК на базе Intel Core i7 с картой Nvidia GeForce GTX 1080Тi в течение 150 эпох. Мы провели дискретизацию облака точек на основе kNN с k = 20 . Был проведен сравнительный анализ предложенного метода сегментации с известными методами 3D сегментации и разными комбинациями входных признаков облаков точек, исследовано влияние на точность сегментации способа формирования облака точек: в первом случае исследовалось облако точек из эталонного набора данных (табл. 2 и табл. 4) , во втором случае применены варианты с использованием 3D регистрации на основе алгоритмов NICP И FICP (табл. 3 и табл. 5) .

Моделирование показало превосходство предложенного метода по всем метрикам над Point Net, Point Net++ и DGCNN, для RGCNN и DGCNN+RGB получены близкие по точности результаты по метрике F1 и лучшие результаты по метрике Mean Acс. Использование методов регистрации для формирования облака точек ожидаемо приводит к уменьшению точности процедуры его сегментации, однако метод FICP [17] имеет преимущества по сравнению с NICP.

( ^a )

Рис. 3. Результаты повышения плотности облака точек с использованием алгоритма PU-GCN на примере археологического памятника вблизи п. Каменка: a) облако точек до применения алгоритма повышающей дискретизации b) облако точек после применения алгоритма повышающей дискретизации (класс 0 — «фон», класс 1 — «жилищная впадина»)

(b)

Заключение

В работе предложен метод семантической сегментации нерегулярных облаков точек на основе мультимодального взвешенного динамического графа DGCNN*. Архитектура сети использует принцип динамического определения соседства точек в облаке на основе данных о геометрии облаков точек и данных о цвете, что позволяет устранить главный недостаток DGCNN и RGCNN, связанный с размерностью обрабатываемых облаков точек. Структура полносвязного слоя в виде метрического классификатора из двух MLP сетей и RFB сети с конкатенацией данных, получаемых с EdgeConv слоев сети, позволяет эффективно обрабатывать локальные и глобальные признаки объектов. Предложенный метод позволяет получать точное решение задачи семантической сегментации для разреженных, зашумленных и неоднородных облака точек, для 3D сцен с микрорельефом и объектами невыпуклой формы, что важно при обработке геопространственных данных. Метод независим от способа сбора данных: показывает достаточно высокую точность для облаков точек, полученных с использованием вариантов алгоритма ICP.

Исследование выполнено за счет гранта РНФ (проект 23-11-20007).