Селективные свойства неоднородного слоя полупроводниковой плазмы
Автор: Панин Дмитрий Николаевич, Адамович Людмила Владимировна
Журнал: Инфокоммуникационные технологии @ikt-psuti
Рубрика: Теоретические основы технологий передачи и обработки информации и сигналов
Статья в выпуске: 1 т.13, 2015 года.
Бесплатный доступ
Статья посвящена исследованию с помощью численных методов частотно-избирательных свойств полупроводникового слоя плазмы с неоднородной концентрацией частиц
Фильтр, ослабление, полупроводниковая плазма, неоднородный слой, метод дифференциальной прогонки, коэффициент отражения, коэффициент прохождения, полоса пропускания фильтра, полоса задерживания фильтра, переходная область
Короткий адрес: https://sciup.org/140191734
IDR: 140191734 | УДК: 533.9.01
Текст научной статьи Селективные свойства неоднородного слоя полупроводниковой плазмы
За последние годы резко возросли уровень и объем требований, предъявляемых к частотным характеристикам устройств, в которых используется диапазон сверхвысоких частот (радиорелейные линии, радиолокаторы, радиотелескопы и др.) [1-4]. Так как по длине волны излучение СВЧ-диапазона является промежуточным между световым излучением и обычными радиоволнами, оно обладает некоторыми свойствами и света, и радиоволн. Многие радиолокационные антенны и другие СВЧ-устройства представляют собой как бы увеличенные варианты оптических элементов типа зеркал и линз [5].
В то же время СВЧ-излучение сходно с радиоизлучением вещательных диапазонов в том отношении, что оно генерируется аналогичными методами. К СВЧ-излучению применима классическая теория радиоволн [6], и его можно использовать как средство связи, основываясь на тех же принципах. Но благодаря более высоким частотам оно дает более широкие возможности передачи информации, что позволяет повысить эффективность связи. В настоящее время направляющая система, помимо собственно фидера (волновода, коаксиальной линии и т.п.), включает большое число различных фидерных устройств: фильтрующих, согласующих, ответвляющих, суммирующих и других [7].
Фильтры – это основной элемент многих радиотехнических устройств. Они используются для разделения или сложения сигналов разных частот в многоканальных системах связи или в узлах радиотехнических устройств. Спектр электромагнитных колебаний ограничен, и его отдельные участки необходимо отделить один от другого; фильтры используются для того, чтобы излучения радиопередатчиков были ограничены заданными пределами спектра; и наоборот, другие фильтры используются для защиты приемников от помех, расположенных вне их рабочей полосы частот. Частотные характеристики фильтров должны удовлетворять жестким требованиям; соответствующий этим требованиям расчет систем называют синтезом.
В настоящей работе численными методами исследуются частотные зависимости ослабления электромагнитной волны, падающей на неоднородный слой полупроводниковой плазмы под произвольным углом [8]. Показано, что полупроводниковый слой плазмы ведет себя подобно фильтру верхних частот.
Взаимодействие электромагнитной волны с неоднородным слоем плазмы
Рассмотрим неоднородный слой полупроводниковой плазмы, расположенный в координатных плоскостях декартовой системы координат.
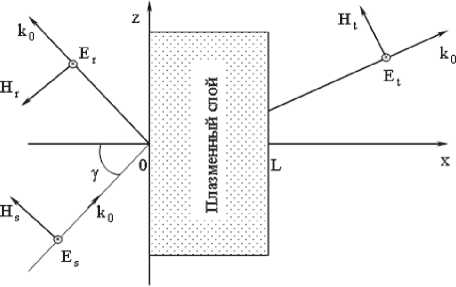
Рис. 1. Наклонное падение для волны с Е-поляризацией
В качестве примера приведем геометрию задачи падения на границу слоя под углом у плоской электромагнитной волны Е-поляризации. Пространственные зависимости напряженностей магнитного и электрического полей можно описать следующей нормированной системой уравнений Максвелла.
dU
"dl
= -jKP$;
^ = -J^k(^^)-sin2 /]t/(^),
где: К = k0L – нормированная частота; U^E^E, – нормированная напряженность электрического поля; rtSWSfE, – нормированная напряженность магнитного поля; § = x/L – нормированная координата; Zq — л] Ho / ^0 – импеданс вакуума; ^Q – комплексная амплитуда напряженности электрического поля.
Исходя из условий непрерывности тангенциальных составляющих полей, представим следующие граничные условия, записанные в нормированном виде.
yt0)-^; ut^-T; (2)
F(o)= (l-^)cos/; K(l) = Tcos/, где R – комплексный коэффициент отражения, T – комплексный коэффициент прохождения.
В уравнениях Максвелла (1) фигурирует такая величина, как комплексная диэлектрическая проницаемость плазмы.
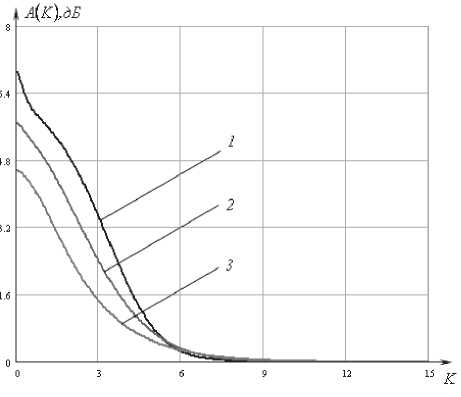
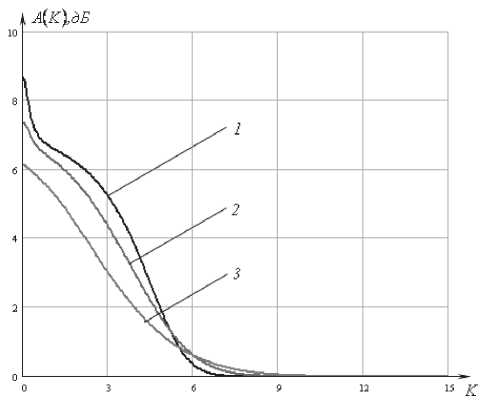
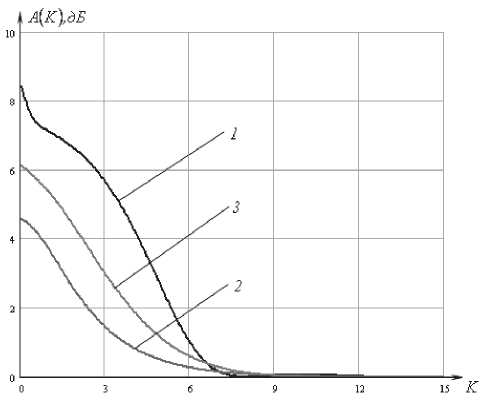
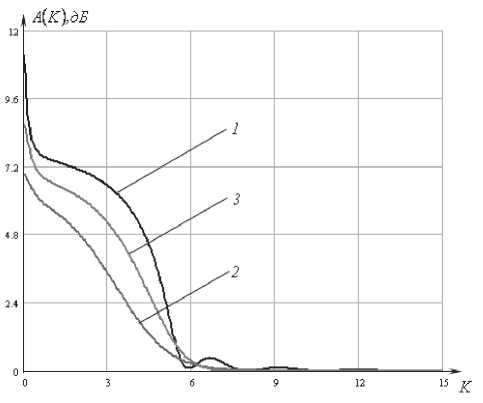
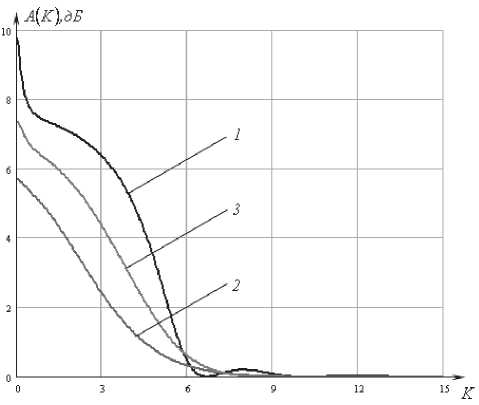
8c к2р^ K^K^ где К (^) – нормированная плазменная частота, к – эффективная частота столкновений. Приведенные уравнения Максвелла (1) и граничные условия (2) составляют так называемую двухточечную граничную задачу. Применяя метод дифференциальной прогонки, удалось свести такую задачу к задаче Коши с начальными условиями. Более того, было получено дифференциальное уравнение, позволяющее определить коэффициент отражения в произвольной плоскости слоя. Представим явный вид дифференциального уравнения, позволяющего рассчитать коэффициент отражения. dR _ (1 - RY cos2у Л|2 - (1 + Ry Л, (4) d§ 2 cos у Следует отметить, что данное дифференциальное уравнение является нелинейным с переменными коэффициентами, поэтому пригодно только для численного решения. Таким образом, рассчитав зависимость коэффициента отражения от частоты, мы можем определить частотную характеристику ослабления, которое вносится слоем полупроводниковой плазмы: параболического профилей при тех же значениях угла падения. Рис. 2. Частотные характеристики ослабления для однородного профиля электронной концентрации полупроводниковой плазмы Нормированная плазменная частота, соответствующая линейному профилю, определяется соотношением вида: ^„te)-«„,(l-|l-2^|). (6) Нормированная плазменная частота, соответствующая параболическому профилю, определяется соотношением вида: ^,(Й = 4^„(1-^. (7) ^,^)=201g Численные результаты и выводы На рис. 2 представлен график частотных характеристик ослабления для однородного профиля электронной концентрации полупроводниковой плазмы при различных углах падения волны Е-поляризации. Кривая 1 соответствует случаю нормального падения; кривая 2 – падению волны под углом 45°; кривая 3 – падению под углом 60°. При этом нормированная плазменная частота K„^=K„, =5 представляет собой максимальную плазменную частоту электронного газа. На рис. 3 и рис. 4 представлены графики частотных характеристик ослабления для линейного и Рис. 3. Частотные характеристики ослабления линейного профиля Рис. 4. Частотные характеристики ослабления параболического профиля Рис. 7. Частотные характеристики ослабления при угле падения 60° Рис. 5. Частотные характеристики ослабления при нормальном падении волны Рис. 6. Частотные характеристики ослабления при угле падения 45° Во всех расчетах нормированная эффективная частота столкновений Kv = 0,5. На рис. 5 изображены частотные характеристики ослабления однородного (кривая 1), линейного (кривая 2) и параболического (кривая 3) профилей при нормальном падении волны. На рис. 6 и рис. 7 представлены характеристики ослабления однородного (кривая 1), линейного (кривая 2) и параболического (кривая 3) профилей при углах падения 45° и 60° соответственно. Анализ полученных результатов показывает, что при изменении угла падения волны происходит смещение характеристик ослабления в частотной области, что делает возможным изменять положение полосы пропускания и задерживания фильтра. В полосе задерживания ослабление, вносимое однородным слоем плазмы, больше, чем ослабление, вносимое неоднородным слоем. Однако в полосе пропускания ослабление, вносимое однородным слоем, носит неравномерный характер и значительно превышает ослабление, вносимое неоднородным слоем. В переходной области фильтра наилучшую крутизну ослабления имеет однородный и параболический слои плазмы. Из всего можно сделать вывод, что при проектировании фильтров СВЧ-диапазона лучше всего воспользоваться частотной характеристикой ослабления, вносимого полупроводниковым слоем плазмы с параболическим профилем электронной концентрации. Именно эта характеристика имеет большую крутизну нарастания в переходной области по сравнению с линейным профилем и меньшее ослабление в полосе пропускания по сравнению с однородным профилем. Данные частотной зависимости модулей коэффициентов отражения можно использовать в экспериментах по электромагнитной диагностике плазмы, в частности, при исследовании степени ее неоднородности. Также полученные результаты будут полезны при проектировании более сложных систем связи, предназначенных для фильтрации электромагнитного излучения СВЧ-диапазона. Устройства такого типа найдут применение в системах высокоскоростной связи на близком расстоянии, в системах обеспечения безопасности, исследовании космоса.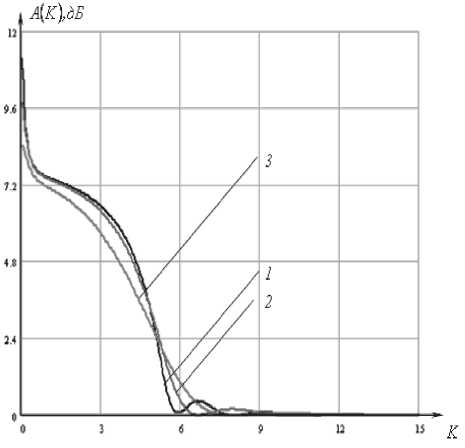
Список литературы Селективные свойства неоднородного слоя полупроводниковой плазмы
- Неганов В.А., Осипов О.В., Раевский С.Б., Яровой Г.П. Электродинамика и распространение радиоволн. М.: Радио и связь, 2005. -648 с.
- Бочкарева Т.С., Неганов В.А., Осипов О.В., Соболев В.А. Электродинамика и распространение радиоволн. М.: Радио и связь, 2003. -324 с.
- Неганов В.А., Раевский С.Б., Яровой Г.П. Линейная макроскопическая электродинамика. Т. 1. М.: Радио и связь, 2000. -509 с.
- Виноградова М.Б., Руденко О.В., Сухоруков А.П. Теория волн. М.: Наука, 1979. -383 с
- Кугушев А.М., Голубева Н.С. Основы радиоэлектроники. Линейные электромагнитные процессы. М.: Энергия, 1969. -879 с.
- Гинзбург В.Л. Распространение электромагнитных волн в плазме. М.: Наука, 1967. -684 с.
- Зайцев В.В., Панин Д.Н., Яровой Г.П. Компьютерный синтез плавных согласующих переходов//Физика волновых процессов и радиотехнические системы. Т.5, №2, 2002. -С. 59.
- Петров Б.М. Электродинамика и распространение радиоволн. М.: Радио и связь, 2000. -559 с.


