Sensitivity Analysis Using Simple Additive Weighting Method

Published Online May 2016 in MECS

Multiple criteria decision making (MCDM) is used when a decision maker wishes to find the best alternative or rank a list of alternatives in a rational and efficient manner when multiple decision criteria are involved. One of the earliest MCDM methods used is the simple additive weighting (SAW) [1],[2],[3],[4]. The SAW method is largely used in the management discipline for selection of suppliers, projects and facility locations [5], [6], [7]. However, the SAW method is less used in the research community in favour of other methods such as the Analytic Hierarchy Process (AHP) [8], [9], [10] and Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) [7],[8],[11],[12].

In a MCDM problem there are four components, namely: (1) alternatives, (2) criteria, (3) relative importance (weights) of each criterion, and (4) criterion values for each alternative. A decision table consisting of these four components is shown in Table 1. The decision table shows alternatives, Д[ (1 < i < н ), criteria, Cj (1 < j < m), weights of criteria, Wf (1 <  j < m ) and the measures of performance of alternatives, Xy.

There are four main steps in the formulation of MCDM problems:

• 1.    Determining the relevant criteria and alternatives.

• 2.    Ascertain the measures of performance of the

• 3.    Attaching numerical measures to the relative importance (criteria weights)

• 4.    Application of an algorithm on the numerical values to determine a ranking of each alternative.

alternatives in terms of the selected criteria.

Quantitative decision methods like the SAW and TOPSIS takes the decision table given in Table 1 as input and produces a ranked set of alternatives. Although this output could be useful to decision makers many times decision makers wish to analyze the impact of changes to criteria data given the fact that some of the data in the first place may be uncertain. This process is called sensitivity analysis (SA) [13],[15] and helps the decision maker compare different scenarios and their potential outcomes based on changing conditions. In management decisions involving selection of suppliers, projects and procurement of assets often involve sensitivity analysis. Since SAW is a commonly used MCDM method in the management discipline it is important to have a robust approach to sensitivity analysis as it relates to the SAW method.

Table 1. Components of a Decision Problem

Weights W'!   w:   w3w

Criteria Ct    G    C5C

Alter natr;es

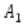
X11   x12   x13

"21  "22  x23"2тп

X31  Xg;  XggXg

^nl  ^n2  ^nl*nm

Linear Programming (LP) provides a natural framework for SA which is typically done after the optimal solution to the problem is determined. The SA is said to be a post-optimality step. The decision maker wants to see how sensitive an optimal alternative is to changes in the constraints and the objective function. However, research on SA in MCDM methods is limited with respect to post-optimality step approaches.

To capture the advantages that the LP method has as it relates to SA, we proposed an extension of the SAW method called Sensitive - Simple Additive Weights (S-SAW) method which due to its use of an objective function provides a framework for a novel approach to sensitivity analysis which does not involve weight changes or changes to alternatives criteria values. Like the LP approach, selected changes are made to the objective function and the impact of the optimal alternative is studied.

This paper is organized as follows. Section II gives an overview of existing approaches to sensitivity analysis in MCDM methods. The SAW method and the S-SAW method which can be seen as an extension to the SAW method are described in Sections III and IV respectively. The S-SAW method for sensitivity analysis is discussed in Section V and examples to show how the new approach to sensitivity analysis works are provided. Section VI introduces mathematical insights of how the S-SAW method works. Finally, the last section presents the conclusion of the proposed method.

• II.    Existing Approaches to Sensitivity Analysis

A lot of research on SA as it relates to MCDM methods is focused on the assessment and influence of criteria weights [14], [15], [16] with the goal of determining how critical each criterion is. The conclusions of [14] suggest that the most sensitive decision criterion is the one with the highest weight, if weight changes are measured in relative terms. This approach is limited because it does not address the combine impact of selected criteria on the ranked alternatives.

The authors of [14] presented a complex sensitivity analysis approach which deals with the change of the values of the alternatives against the criteria. A fixed set of criteria weights are used in the sensitivity analysis process to determine the range of values that a given criterion can have without altering the rank order of the alternatives given that all other criteria weights are kept constant. This approach is useful but is very involved and requires a lot of effort to determine the change to a given criterion for a particular alternative which would invoke a rank change in that alternative.

SA in MCDM is often not done as a post-optimality step like in the LP approach. Many approaches [14], [18] use Monte Carlo Simulations methods for the generation of data sets based on the initial data. These data sets are then used to study how slight variations of the initial criteria data values result in the changes of ranking of the optimal alternative. In this way, decision makers will know what impact each criterion has on the optimal alternative. The main drawback of this approach is that it is computational intensive.

When Monte Carlo methods are used with MCDM techniques [3],[18],[19] the result is that a definitive answer is not provided due to the fact that the inputs are stochastic in nature. As a result these approaches can lead to complex interpretations about the risks associated with solutions.

Considering the reviewed gaps in sensitivity analysis involving Monte Carlo MCDM techniques and the drawbacks of the post-optimality approaches of [14], [15], [16] this paper introduces a post-optimality approach which uses an objective function where selected changes are made to the objective function and the impact of the optimal alternative is studied.

• III.    SAW

The SAW MCDM method is very simple and popular. The method takes the decision table shown in Table 1 as input and produces a ranked set of alternatives. There are two types of evaluation criteria: benefit and cost criteria. A benefit criterion means that the higher the value of the criterion the better the value is for a given alternative. For example, if a customer has a choice between two Internet Service Providers (ISPs) A [bandwidth = 500 Mbps, price = $200] and B [bandwidth = 200 Mbps, price = $50], and the criteria are price and bandwidth, then bandwidth is a benefit criterion since a customer would want higher bandwidths. On the other hand, price is a cost criterion since a customer would want to minimize the price he pays for the service.

A key part of the SAW method is the normalization process, which takes criteria performance values and transform them to dimensionless units. The larger the normalized value becomes, the more preference it has. There are basically two approaches to normalization:

• 1.    Distance-Based Normalization Methods [20] – this invloves measuring the eucludian distance from origin for each criterion

• 2.    Proportion Based Normalization Methods - the proportion of difference between performance value of the alternative and the worst performance value to difference the between the best and the worst performance values [21]

The SAW method can be used with different normalization procedures. In this paper, we use the Linear Scale Transformation, MaxMin method [2], [22] which is a proportion based normalization method. Using this method the decision matrix given in Table 1 is normalized by equations 1 and 2:

C^ij-^) .                л

Zv “ <агЪ)У 1-1.....n'jeflb faj-Xi^ _

2ц =-------, i = l,...,n; / E 12, y t-r6/!

where ZU are normalized criterion values, ci is the max (Xy) for criterion / and, ^j is the min(xy) for criterion /, ^6 and n£ are, respectively, the sets of benefit and cost criteria. Associated with each criterion column. / in the decision matrix zij is weighting u^- such that

^=i ч = 1 . The overall assessment of each alternative is computed by Equation 3. The greater the value Ji means that the alternative is ranked higher.

Я = ^7=1 zywr ‘ = 1.....n          (3)

• IV.    S-Saw Method

The S-SAW method can be seen as an extension of the SAW method. The major difference is that the S-SAW allows the decision maker to define an objective function which governs the optimization goals of each criterion. This concept of optimization will be formally defined in Section V1. The first step in the S-SAW method is to normalized the decision matrix given in Table 1 by using equations 4 and 5:

2№j-br3

2ц =          — 1, i = 1,..., n;/ 6 П^ (4)

У (Cj-bj)                       "      °

2(Хц-ЬЛ z^ = 1 — —-—7—, i = 1,..., n;/ E Oc (5)

4        ^j-bj)               J c where Z4 are normalized criterion values, Qj is the max (Xy) for criterion / and, ^f is the min(Xy) for criterion J, Оь and n£ are, respectively, the sets of benefit and cost criteria. The zy matrix has dimensionless values in the range [-L1] . The function which transforms the matrix Xy to Zy can be any monotonic continuous increasing or decreasing function whose range exists on [-L1] .

The proposed S-SAW method has a F function which accepts a criterion j and maps it to the set {-1,0Л}. That is F*0) E (-1,0,1} where j e (1,2,..., m}. The value for / is decided by the decision maker and F*Q") is called the objective coefficient.

Key to the S-SAW method is Equation 6. After the matrix multiplication process the Ус position with the largest value represents the preferred alternative. An analysis of the S-SAW method will be given in Section

VI.
	"xn Z12	' Ztinl pVlF41) "	У1"
	Z21 z22	• z2m W2F‘(2)   _	№	(6)
	-Znl Zn2	■ znmJ LwmF*(m).

The S-SAW algorithm has a special property which the SAW algorithm does not possess. This is the ability for the decision maker to express which criteria are to be optimized, ignored or minimized. This special property is achieved via the use of an objective function which should not be confused with criteria weights. In other words, the decision maker has more power to customize the type of alternatives the decision system produces. The SAW only allows the decision maker to consider criteria weightings.

• A. S-SAW Examples

Table 2 shows a decision problem with 5 alternatives and 5 decision criteria. The decision matrix before normalization shows the ^j and ^/ values for each criterion. Using Equations 4 and 5 the data is normalized and then Equation 6 is used to produce Ус . The rank order of the alternatives is shown in the column labelled "Rank". Table 2 has a value of 1 for the optimization coefficient value of each criterion, meaning that alternatives which "optimize" values for all or most criteria will be ranked higher.

The data in Table 3 is similar to Table 2 with the only difference that each optimization coefficient value is set to -1, meaning that alternatives wth minimum values for all or most criteria will be ranked higher. Notice that the rank order in Table 2 is A_t>A₃ >A₄>A₂> Л₅and the rank order in Table 3 is Л₅ >  A_z > Л₄ > Л₃ > л_г which is a complete reversal of the order.

Table 2. Example of S-SAW operation under optimization function F^* (j)=1 for j=1,...,m

	Decision Matrix						Normalized Decision Matrix
Criteria	Ci	Cz	Ca	C4	Cs	Cl	Cz	Co	C4	C=	и
	0.41	0.013	0.30	0.06	0.22	0.41	0.013	0.30	0.06	0.22
Opt. Goal						1.00	1.00	1.00	1.00	1.00		Rank
Ai	0.36	0.25	0.29	0.30	0.32	0.98	0.63	0.95	0.83	0.73	0.91	1
4,	0.36	0.28	0.04	0.09	0.02	1.00	1.00	-1.00	-0.82	-1.00	-0.13	3
Ад	0.03	0.17	0.30	0.22	0.26	-1.00	-0.14	0.95	0.22	0.41	-0.03	4
A*	0.16	0.20	0.30	0.07	0.03	-0.19	0.13	1.00	-1.00	-0.92	-0.04	2
As	0.10	0.09	0.08	0.32	0.37	-0.58	-1.00	-0.66	1.00	1.00	-0.17	5
BJ	0.36	0.28	0.30	0.32	0.37
bi	0.03	0.09	0.04	0.07	0.02

Table 3. Example of S-SAW operation under optimization function F^* (j)=-1 for j=1,...,m

	Decision Matrix						Normalized Decision Matrix
Criteria	^1	^2	с3	С4	С5	С1	^2	Сэ	С4	С5	к
ч	0.41	0.013	0.30	0.06	0.22	0.41	0.013	0.30	0.06	0.22
Opt. Goal						-1.00	-1.00	-1.00	-1.00	-1.00		Rank
Ai	0.36	0.25	0.29	0.30	0.32	0.98	0.63	0.95	0.83	0.73	0.17	5
	0.36	0.28	0.04	0.09	0.02	1.00	1.00	-1.00	-0.82	-1.00	0.13	2
	0.03	0.17	0.30	0.22	0.26	-1.00	-0.14	0.95	0.22	0.41	0.04	4
■4 4	0.16	0.20	0.30	0.07	0.03	-0.19	0.13	1.00	-1.00	-0.92	0.03	3
^5	0.10	0.09	0.08	0.32	0.37	-0.58	-1.00	-0.66	1.00	1.00	-0.91	1
9	0.36	0.28	0.30	0.32	0.37
	0.03	0.09	0.04	0.07	0.02

Table 4. Example of SAW operation. There is no concept of an optimization

	Decision Matrix						Normalized Decision Matrix
Criteria	Cl	Сц.	с3	С»	С5	С1	Сц.	са	С»	С5	к
ч	0.41	0.013	0.30	0.06	0.22	0.41	0.013	0.30	0.06	0.22
Ai	0.36	0.25	0.29	0.30	0.32	0.99	0.81	0.98	0.91	0.87	0.95	1
Ад	0.36	0.28	0.04	0.09	0.02	1.00	1.00	0.00	0.09	0.00	0.43	3
А 2	0.03	0.17	0.30	0.22	0.26	0.00	0.43	0.97	0.61	0.71	0.48	4
^4	0.16	0.20	0.30	0.07	0.03	0.40	0.57	1.00	0.00	0.04	0.48	2
А 5	0.10	0.09	0.08	0.32	0.37	0.21	0.00	0.17	1.00	1.00	0.43	5
=1	0.36	0.28	0.30	0.32	0.37
	0.03	0.09	0.04	0.07	0.02

Table 5. Examples of how the S-SAW method is used to calculate the Sensivitiy measures: MIRR and LIRR

Ci ^2 Ci Сд C= Rank Order Change? Ratio 0.41 0.013 0.3 0.06 0.22 F4G) = 1 1 1 1 1 1 Д  4    >4 >4 F*(p)=-1 -1 1 1 1 1 4 > 4 >4 >4 >4 Yes 1|5 (MIRR) F'^ = 1 1 1 1 1 1 4 > 4 >4 >4 >4 F‘№ = -1 1 -1 1 1 1 4 >4 >4 >4 >4 No F"(p) = -1 1 -1 1 -1 1 4 >4 >4 >4 >4 No F"(p) = -1 1 -1 1 -1 -1 4 > 4 >4 >4 >4 No F*fr) = -1 1 -1 -1 -1 -1 4 >4 >4 >4 >4 Л2 / Л£ / л5 / л3 / Л4 Yes 4|5 (LIRR) the preferred optimal alternative is no longer optimal.

The SAW method is a special case of the S-SAW method where the optimization coefficient value of each criterion is set to 1. Table 4 shows the SAW method output for the same data as in Table 2. The main difference is that the SAW method normalization matrix values exists on [ОД] rather than [-Ы] . The final ranking is A_t>A₃ > А₄ > Л₂ > Л₅ . However, the SAW method does not have an optimization option for criteria where the decision maker can have an influence on the rank order of the alternatives based on his optimization preferences.

• V.    Sensitivity Analysis with S-SAW

The approach to sensitivity analysis in this paper focuses on how a collection of criteria impact on the optimal alternative. The objective coefficient for each criterion in the collection is set to either 1 or -1 until

Consider the following definitions:

Most Important Resistant (MIR) Criteria Set -Given a preferred alternative Л^ and a set of criteria С = [1,2.....ш} where F*(/) = 1 for all criteria / Е С, the MIR criteria set М С С is the smallest set of criteria where F*(p) = — 1 р е М that will invoke a change in the rank order such that Л^ is no longer preferred alternative. The criteria p are ordered from highest criterion to lowest criterion weight.

Least Important Resistant (LIR) Criteria Set -Given a preferred alternative Л^ and a set of criteria С = [1,2.....ш} where F*(/) = 1 for all criteria/ЕС, the LIR criteria set МсС is the smallest set of criteria where f*(p) = -1, р Е М that will invoke a change in the rank order such that л^ is no longer preferred alternative. The criteria p are ordered from lowest criterion to highest criterion weight.

Table 6. Modified Decision Matrix

	Decision Matrix
Criteria	Cl	Cj	Cg	C4	C5
^	0.41	0.013	0.30	0.06	0.22
Opt. Goal
Al	0.29	0.25	0.29	0.30	0.32
Az	0.03	0.28	0.04	0.09	0.02
Ao	0.30	0.17	0.30	0.22	0.26
a4	0.16	0.20	0.30	0.07	0.03
A 5	0.16	0.09	0.08	0.32	0.37
aJ	0.36	0.28	0.30	0.32	0.37
bj	0.03	0.09	0.04	0.07	0.02

Table 7. Calculate the Sensivitiy measures: MIRR and LIRR after modification of decision problem given in Table 2

	Ci	Cz	Cg	C4	C5	Rank Order	Change?	Ratio
wi	0.41	0.013	0.3	0.06	0.22
F*№ = 1	1	1	1	1	1	J  4    >4 >4
F*(p) = -1	-1	1	1	1	1	4 >4 >4 >4 >4	No
F*^ = -1	-1	1	-1	1	1	4 >4 >4 >4 >4	Yes	2|5 (MIRR)
F*(p) = -1	1	1	1	1	1	4 >4 >4 >4 >4	No
F*(p) = -1	1	-1	1	1	1	4 >4 >4 >4 >4	No
F*(p) = -1	1	-1	1	-1	1	4 >4 >4 >4 >4	Yes	2|5 (LIRR)

MIR Ratio Let х = |М| where м is the MIR criteria set. Then the MIR Ratio is given by MI RR = x|m where m is the number of criteria in the decision problem.

LIR Ratio Lety= Mwhere L is the LIR criteria set. Then the MIR Ratio is given LI RR = y|m where 772 is the number of criteria in the decision problem.

The MIRR and LIRR are defined in terms of the preferred alternative which results from the S-SAW final ranking. An example of how the MIRR and LIRR are calculated is given in Table 6. The decision data used is given in Table 2.

The MIRR measures how stable the preferred alternative is with respect to minimum values for criteria with the highest weights. The MIRR determines the minimum number of the most important criteria which can be minimized and cause a change in the preferred alternative. The MIRR is given as x|m where x is the smallest number of the most important criteria which caused the change in the preferred alternative. If x is small relative to m this means that the preferred alternative depends heavily on criteria with high weights and these criteria need to be measure with a great degree of accuracy. Table 5 shows a MIRR value of 1|5 or 0.2 for the decision problem which means that the preferred alternative is very sensitive to C i. On the other hand, if MIRR is large this means that the preferred alternative is very stable when there is uncertainty with the most important criteria.

The LIRR measures how stable the preferred alternative is with respect to minimum values for criteria with the lowest weighs. The LIRR determines the minimum number of the least important criteria which can be minimized and cause a change in the preferred alternative. The LIRR is given as y|m where y is the smallest number of least important criteria which caused the change in the preferred alternative. If LIRR is less than 0.3 this means that the preferred alternative depends heavily on criteria with low weights. This situation means that the preferred alternative cannot survive a large degree of uncertainty and that some other alternative is very close to becoming the optimal alternative. Table 5 shows a LIRR value of 0.8 for the decision problem which means that the preferred alternative is sensitive to the set [C:X3X4,C5} since these criteria have the 4 lowest weights. The worse values for C-, Са,Сд and ^5 will invoke a change in the preferred alternative and therefore the decision maker has to be aware of this so that he will not consider this situation if he wishes to maintain the position of the optimal alternative. This value for the LIRR reinforces the conclusion made from the MIRR value which suggests that the decision problem is very sensitive to C 1.

Because Ci has the the highest weighting does not necessary makes the results of the above analysis obvious. Consider, Table 6 which shows a slightly modified decision matrix from the one given in Table 2. The new MIRR value is 2|5 or 0.4 for the modified decision problem which means that the preferred alternative A^ is not as sensitive to criterion c i (which has the highest weighting) as in the previous decision problem.

This is illustrated in Table 7 and it means that the decision maker can tolerant more uncertainty in Cl values. The measurement also suggests that the criteria in the set [CiXg] collectively influence the output.

Similarly, from Table VII the LIRR values for the new decision problem is 2|5 or 0.4 which means that the preferred alternative is sensitive to the set {С:,СМ}.

• VI.    S-SAW Objective Function

The S-SAW objective function is the key for

understanding the rationale for using the MIR and LIR measures for SA. It is important at this time to define the concept of a pareto optimal alternative.

A Pareto optimal alternative is an alternative С1 from a set of alternatives Л , where there exists no other alternative х е 4 such that да^ да for all, / е {1,2, ...,тп}with at least one strict inequality.

Note that the set of alternatives Л may or may not contain a pareto optimal alternative or there may exists a subset А, С ^ of pareto optimal alternatives. Also, С1 is a weak pareto optimal alternative from a set of alternatives Л , when there exists no other alternative х е А such that да <да for all, / 6 {1,2,..., тп}. In this paper the term pareto optimal is used to represent both situations where да <да or f;(«)< ^W for all, / € {1,2,...,m}.

Lemma 1 Given a set of alternatives Л the S-SAW method will rank a pareto optimal alternative as the preferred alternative if the objective function F*G) = 1

.

Proof. Let F*to = 1 for V/ 6 {l,2,..,m} and Зк be the maximum of

У; = 5^7=1 WjZijF’Q) = Х7₌₁ WjZy Vi .

Note that h e {1,2,..,n].

If alternative ^ is not pareto optimal then there is another alternative г for which Zy > )k; V/ and the inequality is strict for at least one j then К > 3k which is a contradiction.

As discussed earlier, when F*G) = 1 for all criteria /, the SAW and S-SAW have the same alternative ranking. According to Lemma 1 the preferred alternative would be an optimal alternative. What about when^‘« =-l for all criteria /? Would the preferred alternative be ranked last in the rank order of alternatives? Consider Lemma 2.

Lemma 2 Given a set of alternatives Л the S-SAW method will rank the preferred alternative as the alternative in the rank order of alternatives if objective function .

Proof. Let F*G) = -1 for v/ e {1,2,..,тп} )k = max(X7=1 M^zyF’Q)) = -Z7=1w;ziv last the

and

From Lemma 1, УЬ has the highest value and it is the preferred optimal alternative. Therefore, -УЬ will be the lowest value and so alternative h е {1,2,..,я}will rank the preferred alternative as the last alternative in the rank order of alternatives.

From Lemma 2, the highest possible value of Jk intuitively means that all criteria have maximum values for ау values in the decision table. When ^ЧП = "I the explanation of why the least ranked alternative is ranked as the preferred alternative is interesting. When Zy < О and F4G) < 0 then the product of the two will be positive. Hence WjZyF‘(j) > 0 for all criteria and therefore .

Lemma 2 justifies why MIR and LIR measures are calculated by first setting F*G) = 1 for all criteria. In the case of the MIR the criteria with the highest weights are set to F4(P) = "I where p e M until the preferred alternative ranking is changed. Each criterion that is minimized will decrease the value of $7=1 WjZtjF*U-) relative to the preferred alternative h E {1,2,..,n} . Higher 1^1 (see Section V) means that more important criteria have to be minimized before there is a different preferred alternative. If |M| is small relative to m this means that the preferred alternative depends heavily on the members of M and therefore a great degree of accuracy must be employed for measuring these criteria.

The range of the SAW normalization is [0,1] and that of the S-SAW normalization is [-1,1]. The justification for using [-1,1] in the S-SAW is simply to make the range symmetric so that an additive inverse exists for each W;ZyF⁴Q) E К for all : and / values. This means that the operation S7₌₁ w_jZijF*^ has meaningful addition. However, in the case of the SAW method where normalization has a range of [0,1] , the ^Zy product does not have an additive inverse on [0,1] . This means that the addition operation is compromised.

• VII.    Conclusion

An extension of the SAW method called Sensitive Simple Additive Weights (S-SAW) method is proposed which allows a decision maker to do sensitivity analysis as a post-optimality step like in linear programming. The method introduces an objective function for criteria and uses this function to minimize or maximize criteria optimization goals. Two quantitative measures: MIRR and LIRR are introduced which allows the decision maker to measure different sensitivity aspects of the decision problem which informs the decision maker of the degree of risk he should allow for a given criterion or groups of criteria.

By using examples it is shown that the introduced quantitative measures helps the decision maker to determine which criterion or group of criteria influences the stability of the preferred alternative and gives a qualitative insight into which criteria can tolerant uncertainty. Therefore, using the S-SAW approach would help deciaion makers better evualtae risks associated with decision criteria.