(очевидно, что этот способ может применяться только в случае относительно легкоплавких металлов), а во-вторых, в чистом виде он не особо эффективен при разделении металлических жидких смесей, состоящих из близких по атомной массе компонентов. Помимо всего прочего, центрифугирование не подходит для тонкой очистки металлических расплавов от примесей. Тем не менее, разделение таким путем жидких металлов на компоненты довольно часто используется как на производстве, так и в научных целях. В частности, некоторое время к центрифугированию активно прибегали для управления процессами массопереноса в гетерогенных металлических расплавах, чтобы влиять на микроструктурные свойства сплавов после их солидификации.

Работа [1] посвящена изучению свойств бинарных металлических расплавов c эвтектической диаграммой состояния. Эвтектическая композиция представляет собой жидкий раствор, для сплавов данной системы кристаллизующийся при наиболее низкой температуре. По результатам анализа различных характеристик смесей, а именно, теплоты смешения в зависимости от процентного соотношения компонентов, был сделан вывод, что наиболее сильная несмешиваемость наблюдается в композициях с максимальной теплотой смешения. Показано, что процентный состав сильно отличается от эвтектического, если смесь кристаллизуется при более низкой температуре. Так как состояние равновесия фаз контролируется не только температурой, но и давлением, то в [1] сделан вывод, что расслоение расплавов c эвтектической диаграммой состояния достижимо путем центрифугирования.

Разделение на фазы может проявляться совсем незначительно на уровне микрогетерогенного строения, другими словами, в таких смесях будут наблюдаться небольшие конгломераты, состоящие преимущественно из атомов одного вида. Наличие подобной перемежаемости областей с преимущественно разным составом традиционно связывают с неполной смешиваемостью. В работе [2] предпринята попытка изучить влияние центробежных сил на микроструктуру металлического расплава Sn–Bi (олово–висмут). Его помещали в центрифугу и подвергали достаточно быстрому вращению (до 3000 об/мин, что соответствовало ускорению, в 2000 раз превышающему ускорение свободного падения). Система выдерживалась в таких условиях в течение 10–30 мин, после чего охлаждалась без остановки центрифуги. В результате определялось распределение концентрации компонентов полученного сплава, а именно, анализировалась микрогетерогенность смеси.

Умение управлять микрогетерогенностью смеси имеет серьезное прикладное значение. В работе [3] изучалось крупномасштабное перераспределение углерода в расплаве чугуна ЛК-4. В эксперименте однородная смесь помещалась в алундовые капилляры диаметром 1 мм или кварцевые трубки диаметром 5–6 мм. Высота образцов, соответственно, равнялась 15–16 см. После выдержки в вертикальном положении при температуре ~1000°С в течение 3 ч образцы быстро охлаждали. В итоге фиксировалась небольшая продольная разность концентраций углерода (~0,2%) во всех образцах. Выдержка образцов в горизонтальном положении не приводила к перераспределению концентрации вдоль капилляра. Попытка объяснения экспериментальных данных была сделана на основе теории броуновского движения в жидкостях. Асимптотическое решение на сколь угодно больших временах зависело от характерного радиуса частиц, оценка которого предполагала его совпадение с величиной микрогетерогенных областей в работах по центрифугированию.

В то же время, результаты исследования микрогетерогенности методом центрифугирования были подвергнуты справедливой критике в [4]. Исходя из анализа предшествующих экспериментальных работ по центрифугированию металлических расплавов эвтектического типа, был сделан вывод, что конечный градиент концентрации не связан напрямую со временем центрифугирования и частотой вращения. Проведя ряд теоретических оценок, авторы пришли к заключению, что кристаллизация смеси должна оказывать сильное влияние на конечное распределение концентрации. Также было предложено объяснение сильного разброса данных при сравнении разных экспериментов, заключающееся в следующем: в процессе солидификации сплава эвтектического типа происходит его разделение на кристаллики чистых компонентов (подобный распад имеет место даже при очень быстром охлаждении: ~105 град/сек); пока весь сплав не затвердеет, эти кристаллики, в зависимости от соотношения их плотности и плотности расплава, будут всплывать или оседать. Наличие такого движения в смеси может сильно исказить ее микроструктуру, что делает центрифугирование не вполне однозначным методом управления микрогетерогенностью.

Описанное выше поведение гетерогенных расплавов в центрифугах определяется исключительно объемными механизмами. При рассмотрении движения смесей по микроканалам на передний план начинает выступать взаимодействие флюида со стенками. Процессы перераспределения компонентов в жидких смесях при заполнении ими тонких слоев или каналов обладают общими чертами. Это касается не только гетерогенных расплавов металлов, но справедливо и в отношении самых разных по своей природе жидких смесей. В [5] была аналитически решена задача о влиянии термодиффузии на гравитационное оседание наночастиц в несущей жидкости, находящейся в тонком вертикальном неоднородно нагретом канале. Точное аналитическое решение в виде рядов позволило проследить за эволюцией полей температуры и концентрации наночастиц для разных значений коэффициента термодиффузии. Показано, что полученное решение может быть положено в основу методики экспериментального измерения коэффициента термодиффузии для наножидкостей, что является весьма актуальным применительно к магнитным жидкостям, физические свойства которых сильно отличаются друг от друга ввиду разных способов создания подобных сред. Установлено, что для размеров феррочастиц ~10-20 нм гравитационное оседание может привести к заметному эффекту только при длительности процесса порядка ~106–107 с. Иными словами, седиментационные эффекты для наноразмерных феррочастиц в маслах чрезвычайно слабы, а характерные времена оседания измеряются многими месяцами и даже годами.

Напротив, добавление конвективного механизма переноса в модель, как это имело место в работе [6] о самопроизвольном остывании и дальнейшем замерзании водного раствора Na 2 SO 4 в тонком вертикальном капилляре, позволило объяснить с учетом эффекта термодиффузии процесс крупномасштабного продольного перераспределения примеси сульфата натрия вдоль канала за короткое время — порядка 10 мин. Экспериментальные измерения подтверждены количественно путем прямого численного моделирования. Таким образом, в самых разнообразных ситуациях, когда действуют различные по своей природе физические механизмы, относительно быстрое крупномасштабное продольное разделение компонентов жидких смесей в тонких каналах имеет место только при наличии конвективного массопереноса.

В [7] экспериментально зафиксирован и детально описан эффект продольного перераспределения компонентов легкоплавких металлических расплавов с эвтектической диаграммой состояния в тонких капиллярах (высота варьировалась в пределах 40–220 мм, диаметр составлял 0,8–1,2 мм). Алундовый или кварцевый капилляр, заполненный однородной двухкомпонентной смесью жидких легкоплавких металлов (Sn–Pb, Cd-Bi или Al–Si) в вертикальном положении помещался в печь при температуре, когда оба компонента находились в расплавленном состоянии. Спустя ~ 1 ч его вынимали и немедленно остужали. Алундовое покрытие удалялось, после чего изучалось распределение компонентов сплава в продольном и поперечном сечениях. Эксперименты продемонстрировали, что одного-двух часов выдержки в печи вполне достаточно, чтобы продольное разделение смеси выходило на установившееся значение. Измерения показали довольно большой перепад концентрации компонентов вдоль капилляра (5–20%) с характерным экспоненциальным распределением, отвечающим уменьшению концентрации тяжелого компонента с высотой. В случае горизонтального расположения образца в печи перераспределение компонентов вдоль капилляра не наблюдалось.

Следует отметить, что указанные сплавы производили смешением чистых компонентов, содержание основного элемента в которых было не менее 99,9 вес.%. Для получения однородных по составу смесей расплавы перегревали на 300–400°C выше точки плавления и тщательно механически перемешивали в течение длительного времени. Перегрев обеспечивал полную растворимость компонентов друг в друге и предотвращал объединение родственных атомов в кластеры.

Попытка объяснить результаты опытов [7] за счет седиментации кластеров атомов предпринята в [8]. Однако этот подход не нашел подтверждения. Расчетное время седиментации оказалось на много порядков больше, чем в экспериментах даже для достаточно крупных по величине конгломератов, вообще не содержащих чужеродные атомы. В ходе последующих экспериментов состав этих частиц, а также их радиус, который в теории играл роль подгоночного параметра, так и остались неопределенными. Попытка оценить радиус этих частиц на основе данных рентгеноструктурного анализа тоже не дала положительного результата.

Качественно воспроизвести в расчетах время разделения удалось в работе [9] путем включения в модель специфического поверхностного механизма массопереноса. Исходя из полученного в экспериментах радиального распределения компонентов в различных сечениях было сделано предположение, что тяжелый компонент расплава за счет некого механизма выносится на поверхность, где «стекает» вниз как по свободной поверхности и диффундирует обратно в объем в нижней части капилляра. Подобное поведение тяжелого компонента свидетельствует об отсутствии в системе термодинамического равновесия, что должно порождать специфические по своей природе термодинамические силы и потоки, стремящиеся установить в системе состояние равновесия. В данном случае роль термодинамической силы может играть градиент температуры. Если специально не контролировать распределение температуры в рабочей камере печи, то при перепаде 10–20 см по высоте вполне допустимо образование тепловой шапки с разницей по температуре порядка 1 K. Следовательно, за счет естественных процессов теплообмена на вертикальных гранях капилляра во время выдержки в печи может устанавливаться градиент температуры, направленный вертикально вверх. В силу существенного отличия поверхностных энергий металлического расплава и материала стенок капилляра считается, что на вертикальной границе справедливо условие полного несмачивания. На появившейся таким образом вертикальной свободной поверхности имеет место температурная неоднородность поверхностного натяжения, которая приводит к генерации термокапиллярного течения. Помимо этого, учитываются механизмы адсорбции и десорбции тяжелого компонента на свободной поверхности.

Численное решение полных нелинейных уравнений термоконцентрационной конвекции в [9], основанное на данной модели, показало возникновение опускного течения на поверхности. Примесь, скапливающаяся в нижней части капилляра, вследствие десорбции проникала в объем и за счет подъемного конвективного течения в центре капилляра частично переносилась вверх. В итоге создавалось характерное нелинейное распределение примеси вдоль оси канала, которое гораздо лучше согласовывалось с экспериментом, нежели результаты работы [8]. Крупномасштабный перенос компонентов смеси приводил к появлению разности концентраций ~1-5% между торцами капилляра за относительно короткое время (~10 мин). Эффект разделения на компоненты оказался не столь сильным, как ожидалось. Помимо этого, не все использованные параметры соответствовали жидким металлам (Pr = 0,5 ). Тем не менее, в данной работе убедительно показано, что при учете крупномасштабного конвективного переноса за счет температурной неоднородности поверхностного натяжения время разделения и продольный концентрационный профиль могут качественно совпадать с опытными.

Исследования в данном направлении продолжены в [10], где подробно изучалось влияние сопутствующего концентрационно-капиллярного механизма на рассматриваемые процессы. В частности, выявлено, что учет дополнительной концентрационно-капиллярной силы сглаживает все поля, что дает возможность продвинуться в расчетах в область более реалистичных чисел Прандтля (Pr = 0,05) и позволяет получить в расчетах близкие к экспериментальным значениям (20–40%) величины перепадов концентраций на концах капилляра. Однако, в отличие от [9, 10], в экспериментах всегда используются капилляры цилиндрической формы. Поэтому для еще более убедительного согласования результатов прямое численное моделирование процессов разделения бинарного металлического расплава на компоненты в тонком неоднородно нагретом капилляре необходимо проводить для цилиндрической геометрии. В этом заключается цель настоящего исследования.

• 2.    Постановка задачи

  Рассмотрим длинный цилиндрический капилляр с внутренним радиусом R (Рис. 1), целиком заполненный жидкой бинарной смесью легкоплавких металлов. Пусть капилляр расположен в поле силы тяжести, ориентирован вертикально и нагревается сверху так, что на его боковой границе имеет место продольное линейное распределение температуры T = © z/h ( © — разность температур между торцами, h — длина канала в размерных единицах).

  С одной стороны, подогрев сверху подразумевает наличие устойчивой стратификации по плотности за счет теплового расширения    жидкости.    Однако предполагается, что

  двухкомпонентность смеси, а также наличие термокапиллярной силы на боковой поверхности должны обеспечить возникновение циркуляционного конвективного процесса в полости и при соответствующем учете явлений адсорбции-десорбции способны вызвать эффективный массоперенос тяжелого компонента в нижнюю часть капилляра.

  При описании процессов тепло- и массопереноса в объеме жидкой бинарной смеси металлов воспользуемся системой уравнений тепловой конвекции для несжимаемой жидкости в приближении Буссинеска [11]:

  
  
  

  Рис. 1. Геометрия задачи. Система координат

  
  

  | V + ( v -V ) V = -- 1 V p + vA v + g ( в t T -в c C ) Y ,

  d T ,                      „

  — + ( v -V ) T = %A T ,    div v = 0,

  ar ,

  — + ( v -V ) C = D A C .

  d t ^{v 7}

  
  
  
  
  
  
  
  

  Здесь: v , p , T , C — соответственно поля скорости, давления, температуры и объемной концентрации тяжелого компонента смеси; в _t , в C — коэффициенты

  
  

  температурного и концентрационного изменения плотности; р

  
  

  _—

  
  

  плотность

  
  

смеси; %, v, D — соответственно коэффициенты температуропроводности, кинематической вязкости и диффузии в объеме жидкости; g — ускорение свободного падения, γ — единичный вектор, направленный вертикально вверх.

Далее обсудим модель движения на твердой боковой границе, которая напрямую связана с проблемой несмачиваемости, упомянутой выше. Согласно классификации П.Ж. де Жена [12], существуют два типа твердых тел: а) кристаллы с сильной связью (ковалентной, ионной или металлической); б) молекулярные кристаллы (частицы которых связаны силами Ван-дер-Ваальса или, в некоторых частных случаях, водородными связями). Кристаллы с сильной связью обладают «высокоэнергетической поверхностью» со свободной энергией (~ 500-5000 эрг/см²), в то время как у молекулярных кристаллов (как и у молекулярных жидкостей) поверхности «низкоэнергетические» (~ 50 эрг/см²). В результате большинство молекулярных жидкостей полностью смачивают высокоэнергетические поверхности, поскольку величину свободной энергии определяют сильные связи, в то время как энергия взаимодействия твердое тело/жидкость обусловлена силами Ван-дер-Ваальса (между жидкостью и подложкой нет химической связи). В противоположность этому на низкоэнергетических поверхностях, в зависимости от выбранной жидкости и вида подложки, может наблюдаться неполное смачивание. Если роль жидкости играет расплав металла, то эффект несмачиваемости, очевидно, становится еще более вероятным.

Данные рассуждения находятся в полном согласии с тем фактом, что в рассматриваемых в задаче капиллярах, изготовленных из тугоплавких металлов, границы относятся к «высокоэнергетическим границам», эффект разделения бинарных легкоплавких расплавов металлов не наблюдается; он проявляется только в кварцевых и алундовых капиллярах. Следует отметить, что в действительности на поверхности алундовых и кварцевых капилляров имеет место более сложная картина, чем полное несмачивание. Попытки более строго описания граничных условий были сделаны в ряде теоретических исследований (см., например, обзоры О.И. Виноградовой, Е.С. Асмолова и других). Однако, отсутствие достаточной базы экспериментальных данных о структуре и физико-химических свойствах таких поверхностей приводили к появлению неизвестных свободных параметров, используемых в теоретических исследованиях в качестве подгоночных. По этой причине использовать более точные, физически обоснованные граничные условия на поверхности расплав–твердая граница не имеет смысла. Модель полной несмачиваемости вполне приемлема для описания эффекта осредненного движения поверхностного слоя. Как будет видно из результатов расчета, полученная картина явления неплохо согласуется со всеми экспериментальными данными, имеющимися на сегодняшний день.

Таким образом, считая боковую поверхность расплава свободной, можем записать известное уравнение для поверхностной концентрации поверхностно-активного компонента смеси с учетом эффектов адсорбции и десорбции [13, 14]:

|Г + v s ( v -r ) = D s A s Г + k A C - k_D г , (4)

где Г — поверхностная концентрация, k A , k_D — соответственно размерные коэффициенты адсорбции и десорбции, D_s — коэффициент поверхностной диффузии. Индекс s над операторами набла и Лапласа в уравнении (4) означает дифференцирование по координатам поверхности.

Для простоты будем считать, что горизонтальные торцы капилляра являются твердыми и непроницаемыми для вещества. Таким образом, на них выполняются условия прилипания и отсутствия потока вещества:

яг       ас z = 0, h : дГ = 0,    ОС = о,     у = о.

о z           a z

На свободной вертикальной границе учтем простейшим образом явления адсорбции и десорбции. В общем случае интенсивность этих процессов может сложным образом зависеть от меняющихся вдоль канала термодинамических условий. Закон сохранения массы на поверхности, включающий все возможные потоки вещества [15, 16], позволяет связать объемную и поверхностную концентрации следующим условием:

r = R : - D ° C = k.C - k_n Г .

a r A ^D

Далее приведем уравнения (1)–(4) и граничные условия (5), (6) к безразмерному виду, приняв за единицы измерения расстояния, времени, скорости, температуры, давления, объемной и поверхностной концентрации следующие величины: R , R ² / v , x / R , @ , p/v / R ², C 0 , RC 0 . Здесь C 0 — начальная объемная концентрация. Данная единица измерения концентрации весьма удобна при интерпретации результатов в задачах межфазной гидродинамики [16].

После процедуры обезразмеривания уравнения и граничные условия записываются в форме:

| + pr (v-V) v = -Vp + Av + (RaT - Ra С C) y ,   div v = 0,(7)

Pr%+(v-v)T=aT,    °C+Pr(v-v)C=SicaC,(8)

ar+pr v s (vr) = Sc; As r + k+C - k-r,(9)

r = 1: - iSca^ = k+C - k-r, z = 0, H: ^ = 0, If = 0,    v = 0.(11)

a z

В краевой задаче (7)–(11) имеем набор следующих безразмерных управляющих параметров:

Ra = £(Wl,   Ra = gвCC0R3 , pr = v , Sc = f, Sc= ,   k+= kAR,   k = kDR^.(12)

v/ C vx            X D s Ds      + vv

Здесь: Ra , Pr , Sc — числа Рэлея, Прандтля и Шмидта; Sc _s — поверхностное число Шмидта, H — безразмерная высота капилляра в граничном условии (11). Параметры k + , k - имеют смысл безразмерных коэффициентов адсорбции и десорбции, Ra _C — концентрационный аналог числа Рэлея.

Задача решалась в осесимметричной постановке ( д/дЭ = 0 , где 9 — угловая переменная в цилиндрических координатах). В дополнение предполагалось, что v _Э = 0, поэтому описание течения производилось в терминах функции тока у и вихря ф . Соответственно функция тока и вихрь скорости в цилиндрических координатах вводились стандартным образом:

1ду          1 ду vr =" ^, vz ="" ^, r дz            r д r дvr дvz _ 1 д2у 1 ду 1 д2у

---=--Z---Z---1---Z“ .

д z д r r д r ² r ² д r r д z ²

В терминах функции тока и вихря уравнения переноса тепла и уравнения Навье–Стокса, а также уравнения для объемной и поверхностной концентраций (7)–(9) окончательно имели вид:

дф+ И д t r Pr 1 ' ду дф ду дф ф ду ^ ч дz д r д r дz r дz у । _ Л 1 д2у _ дт D дс = Аф         Ra + Ra с , 1         r3 дz2        д r      C д r (13) Pr д Т + дудТ д t дz д r _ ду дТ _ т д r дz А T , (14) д C + X ГдудС — д t Pr ( дz дr ду дС)_ 1 дr дz J = Sc АC , (15) дГ 1 д<дуг^ = sX S+k+C—k—г, Scs дz (16) дt r Pr дz ( дr J где оператор Лапласа в цилиндрической системе координат с учетом осесимметричности решения записывается в форме:

д ² 1 д д ²

A = 7 +----1--7 .

д r ² r д r д z ²

На оси капилляра были приняты стандартные для осесимметричной задачи в цилиндрических координатах граничные условия r = 0: у = -1^ = ф = 0 . д r

При учете на свободной боковой границе термо- и концентрационно-капиллярного механизмов зависимость поверхностного натяжения от температуры и поверхностной концентрации рассматривалась в линейном приближении:

с = c _o — c t T — О р Г ,

где с _т и с_г — соответственно коэффициенты, описывающие связь поверхностного натяжения с температурой и концентрацией. Уравнение баланса касательных напряжений с учетом (18) давало на границе стандартное граничное условие:

r = R :

д v_z

П о

д r       1

д т    дг

Ог     .

д z    ^г д z

Здесь п — динамическая вязкость. После обезразмеривания это граничное условие приводилось к виду:

-            д Т      дГ

r = 1:   ф = Mar —- + Mar —, дz       дz где MaT и MaΓ — температурное и концентрационное числа Марангони:

Ma =σ ^Θ R , Ma =σ C ⁰ R ² . (20) TT ηχ ^ΓΓηχ

Таким образом, в рассматриваемой краевой задаче имелось десять безразмерных параметров (12), (20) и дополнительно безразмерная длина капилляра H .

• 3.    Методика расчета

Система дифференциальных уравнений (13)–(16) совместно с краевыми условиями (10), (11), (17) и (19) решалась методом конечных разностей. Алгоритм был разработан в соответствии с явной схемой решения уравнений в частных производных [17] и основывался на двухполевой методике [18]. При аппроксимации производных по времени и производных по координатам использовались, соответственно, односторонние и центральные разности. Шаг по времени выбирался из соображений устойчивости численной процедуры. При решении уравнения Пуассона для функции тока прибегали к методу последовательной верхней релаксации [17]. В ходе расчетов по времени применялась процедура установления. Компьютерный код был реализован на языке программирования FORTRAN-90. Задача решалась на суперкомпьютере «ПГНИУ–Кеплер» Научнообразовательного центра Пермского государственного национального исследовательского университета «Параллельные и распределенные вычисления». При проведении численного моделирования осуществлялась периодическая запись искомых полей концентрации, завихренности, функции тока и температуры на диск, что позволяло анализировать структуру полей в интересующий момент времени.

Для повышения точности и, как следствие, устойчивости счета в граничных условиях (10), (11) на поток вещества, условии на оси для производной от функции тока (17), а также в нелинейном слагаемом уравнения (16) для поверхностной концентрации производные полей находились при помощи пятиточечных аппроксимационных формул. Роль поверхностных явлений в рассматриваемой задаче является ключевой, так как между поверхностью и объемом идет массообмен поверхностно-активным компонентом. В результате от того, с какой точностью удовлетворяются граничные условия, зависит баланс массы как в объеме, так и на поверхности. Использование простейших аппроксимационных формул первого порядка приводит к генерации схемой несвойственного задаче пилообразного решения вдоль поверхности, которое постепенно устранялось с повышением точности аппроксимационных формул.

Начальными условиями служили невозмущенные поля функции тока ( ψ = 0 ), завихренности ( ϕ = 0), объемной ( C = 0,05) и поверхностной концентрации ( Γ= 4 ⋅ 10 ^{- 3} ). Возмущения в поле температуры внутри капилляра в начальный момент времени отсутствовали ( T = 0), однако на поверхности задавалось ее линейное распределение так, чтобы градиент был направлен вверх и соответствовал нагреву сверху. Для расчетов по координатам r и z применялась сетка 21:311, при этом высота канала бралась много большей толщины и варьировалась в пределах H = 60...110.

Оценим некоторые ключевые безразмерные параметры из общего набора (12), (20), значения которых могут вызвать больше всего вопросов к обсуждаемой задаче. А именно, вычислим их для параметров, соответствующих реальным расплавам металлов: g = 9,8 м/с², β _t = 3 ⋅ 10 ^{- 4} 1/K, Θ= 1K, ν= 3 ⋅ 10 ^{- 7} м²/с, χ= 2 ⋅ 10 ^- 5 м 2 /с, R = 10 ^- 3 м, η= 2 ⋅ 10 ^- 3 Па ⋅ с [19, 20]. В отношении приведенного списка отметим, что температуропроводность металлов в расплавленном состоянии достаточно велика, а радиус капилляра, наоборот, мал, поэтому при подстановке получается значение числа Рэлея Ra = 0,5 , позволяющее оценить его сверху. Коэффициент зависимости поверхностного натяжения от температуры для различных расплавов металлов можно найти в литературе [21]. В частности, для олова σ T = 2 ⋅ 10 ^- 3 Н/(мК). За счет того, что коэффициент температуропроводности у расплавов металлов имеет достаточно большое значение, а радиус капилляра мал, тепловое число Марангони, которое определяется по формуле (20), получается небольшим: Ma _T = 5 . Коэффициент зависимости поверхностного натяжения от концентрации для известных сурфактантов, обычно, на три порядка больше по величине, чем коэффициент зависимости поверхностного натяжения от температуры. В формуле (20) увеличение σ_Γ на три порядка компенсируется дополнительным множителем R = 10 ^{- 3} м, поэтому концентрационное число Марангони должно быть одного порядка с тепловым числом Марангони или чуть меньше.

Вопрос о величинах реальных параметров адсорбции–десорбции для расплавов металлов является более сложным, и авторам, к сожалению, не известны работы с достоверными данными по ним. Численное моделирование показывает, что, в первую очередь, на форму концентрационной вилки сильно влияет отношение коэффициентов адсорбции и десорбции вследствие того, что в рассматриваемой задаче должен соблюдаться определенный баланс между этими процессами. В результате значения этих коэффициентов

Таблица. К анализу сходимости метода

Номер расчета Параметры сетки Относительные погрешности N1 N2 N1⋅N2 ΔEij, % Δψimjax, % 1 7 121 847 – – 2 9 141 1269 23,18 3,764 3 11 161 1771 14,66 1,084 4 13 177 2301 10,14 0,574 5 15 199 2985 7,44 0,399 6 17 229 3893 5,70 0,398 7 19 265 5035 4,51 0,323 8 21 311 6531 3,66 0,313 9 23 369 8487 3,03 0,244 подбирались из условия соответствия формы концентрационной вилки и степени разделения, которые

что наблюдались в эксперименте. Любопытно,

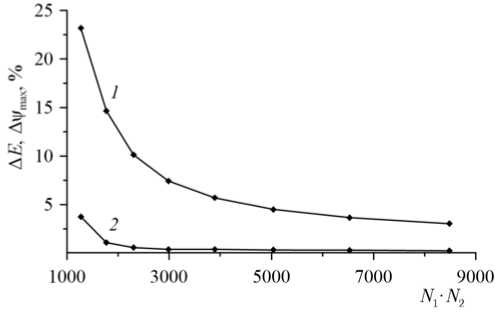
Рис. 2. Относительная ошибка в процентах для кинетической энергии (кривая 1 ) и максимума функции тока ( 2 ) в зависимости от общего числа узлов сетки

концентрационные вилки, похожие по форме на экспериментальные, дают как раз нужный эффект разделения на реальных временах.

Контроль сходимости осуществлялся путем выполнения пробных вычислений на разных сетках. Таблица содержит значения относительных погрешностей счета (в процентах) в зависимости от числа узлов N ₁ (по оси z ) и N ₂ (по оси r ) на этапе установления (приведены изменения величин при переходе с предыдущего уровня точности на текущий).

Данные таблицы визуализированы на рисунке 2 в виде относительных зависимостей суммарной кинетической энергии и максимума функции тока. Графики демонстрируют удовлетворительную сходимость как по максимуму функции тока (локальной характеристике), так и по суммарной кинетической энергии течения.

• 4.    Результаты расчетов и обсуждение

В силу цилиндрической симметрии рассматриваемой задачи всплывающий вдоль оси капилляра поток жидкости растекается в разные стороны по большей площади, нежели в случае канала с плоскими границами при двумерной постановке [9, 10]. Интуитивно понятно, что для обеспечения того же эффекта, что и в плоской задаче, нужны заметно меньшие значения теплового числа Марангони. Это подтверждается прямым численным моделированием и сравнением с результатами из [9, 10].

На рисунке 3 представлены характерные поля объемной концентрации, функции тока и температуры в безразмерный момент времени t = 10⁴ , что соответствует примерно 3 ч. В расчетах использовались модельные значения параметров без привязки к какому-то конкретному расплаву. В сравнении с работами [9, 10] максимум функции тока сдвигается от оси симметрии к внешней границе, то есть изолинии функции тока располагаются плотнее вблизи цилиндрической поверхности капилляра. Изображенные поля демонстрируют процесс разделения изначально однородного расплава на этапе установления. Вследствие подогрева сверху жидкость, опускаясь вниз по внешней границе, постепенно охлаждается. В нижней части капилляра она должна быть в устойчиво стратифицированном состоянии. Иными словами, ее дальнейшее всплытие вдоль оси симметрии обуславливается исключительно законом сохранения массы, то есть нулевым расходом жидкости через поперечное сечение. Термокапиллярная сила создает вдоль поверхности капилляра напорное движение жидкости вниз, в результате чего вдоль оси симметрии канала возникает возвратное течение вертикально вверх.

Опускной поток жидкости обогащен тяжелым компонентом, и архимедова сила препятствует всплытию жидкости, поэтому за счет медленности подъемного движения изолинии температуры практически горизонтальны в поперечном сечении капилляра. Избыток поверхностной концентрации в нижней части капилляра переносится за счет эффекта десорбции в объемную фазу (Рис. 3а). Далее, тяжелый компонент лишь частично переносится возвратным течением в верхнюю часть канала, где он за счет адсорбции снова поднимается на поверхность. Вследствие этого на поверхности формируется достаточно большой перепад концентрации, из-за чего проявляется роль концентрационно-капиллярного механизма, который стабилизирует течение. В результате происходит интенсивное крупномасштабное перераспределение компонентов, выражающееся в возникновении продольного перепада объемной концентрации, составляющего ~20%. При этом на оси капилляра формируется нелинейное распределение концентрации (Рис. 3а), близкое к экспоненциальному, которое хорошо согласуется с экспериментом, но это распределение по своей природе не является барометрическим.

При анализе радиального распределения концентрации обнаружено, что в процессе разделения появляется градиент, направленный к центру капилляра и уменьшающийся с высотой (Рис. 4 б ). Это качественно согласуется с данными эксперимента [22]. Как показали расчеты, изменение полей завихренности и функции тока заканчивается гораздо быстрее, чем разделение смеси на компоненты. Характерные профили продольной компоненты скорости в установившемся режиме приведены на рисунке 4. При использовании набора параметров, соответствующих представленным ранее рисункам, скорость на поверхности имеет практически однородный профиль. Сильные нелинейности проявляются только вблизи торцов капилляра и вызваны как условиями их непроницаемости, так и большим ростом поверхностной концентрации вблизи нижней границы. Так, из рисунка 4 а видно, что уменьшение параметра десорбции k_– влечет за собой заметное увеличение

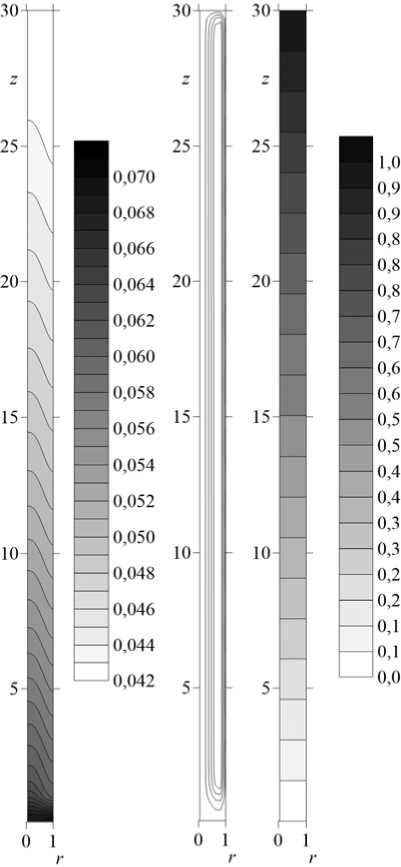
Рис. 3. Поля объемной концентрации ( а) , функции тока ( б ) и температуры ( в ) в момент времени t = 10 4 при Ra = 0,015 , Ra С = 0,05, к + = 2 - 10 ^{- 5} , к - = 6 - 10 ^{- 3}, Sc = 300, Sc , = 180, Ma T = 0,8, Ma _r = 0,4, Pr = 0,045, H = 60 (для лучшей визуализации масштаб делений по вертикали уменьшен в два раза)

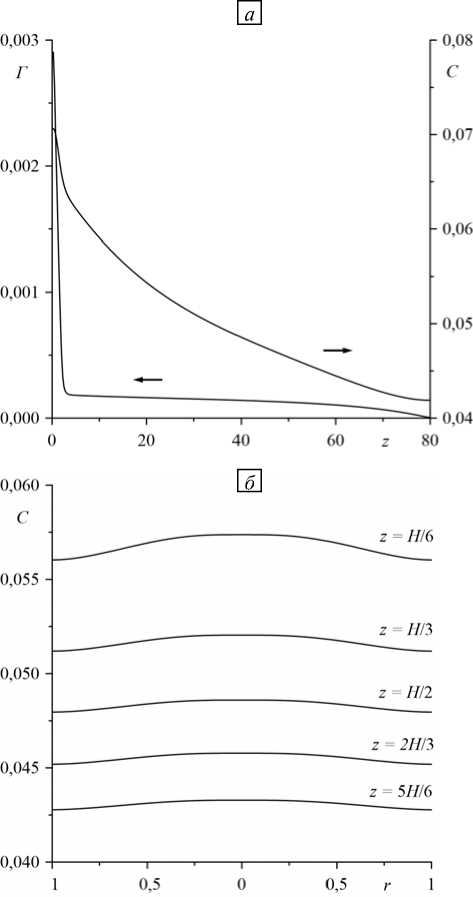
Рис. 4. Продольное распределение поверхностной и объемной концентрации в центре капилляра ( а ) и радиальное распределение объемной концентрации на разных высотах ( б ); значения управляющих параметров см. на рисунке 3

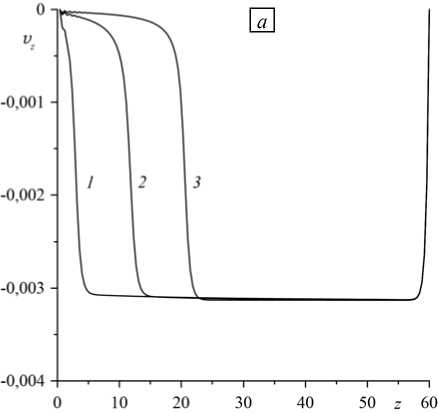
Рис. 5. Продольная компонента скорости на поверхности капилляра при различных значениях k _– ( а ): 4 ⋅ 10^-3 (кривая 1 ), 4 ⋅ 10^-4 ( 2 ), 4 ⋅ 10^-5 ( 3 ), а также теплового числа Марангони Ma _T ( б ): 0,6 (кривая 1 ), 0,8 ( 2 ), 1,0 ( 3 )

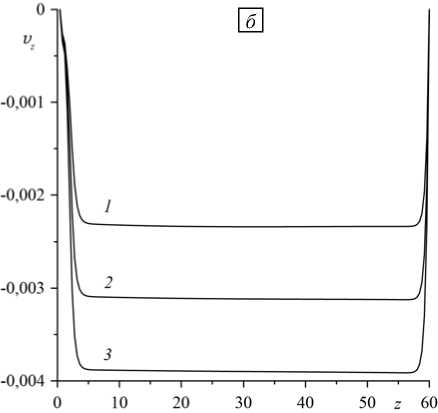
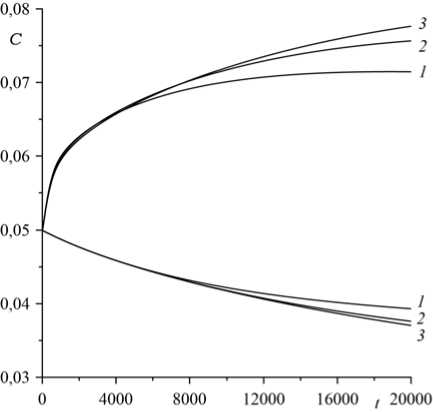
Рис. 6. Максимальное и минимальное значения поля объемной концентрации в зависимости от времени для капилляров разной высоты H = 60 (кривые 1 ), 80 ( 2 ), 110 ( 3 ); другие параметры см. на рисунке 3

размеров участка, на котором происходит сильное торможение поверхностного слоя. При ослаблении десорбционного процесса в нижней части капилляра скапливается большее количество примеси, и за счет упругих свойств поверхностного слоя эффект торможения усиливается.

На величину скорости, в первую очередь, влияет тепловое число Марангони MaT . Увеличение этого параметра приводит к росту скорости переноса компонентов на поверхности (Рис. 5б). При постоянном вертикальном градиенте температуры в рабочем пространстве печи разность температур на торцах растет с длиной капилляра. Поэтому в расчетах тепловое число Рэлея — Ra , и число Марангони — MaT , в которые входит характерная разность температур Θ, изменяются пропорционально длине капилляра (см. Рис. 6). Видно, что с ростом длины капилляра разделение на компоненты интенсифицируется. Это согласуется с экспериментальной работой [8], в которой были продемонстрированы                аналогичные

«концентрационные вилки» для разных длин капилляра. Из результатов расчета следует, что с удлинением канала эффект разделения на больших временах усиливается. При варьировании в разумных пределах значений чисел Марангони, Рэлея, Прандтля, Шмидта и концентрационного аналога числа Рэлея, а также параметров адсорбции и десорбции этот эффект сохраняется.

• 5.    Заключение

Таким образом, прямое численное моделирование показывает, что включение в математическую модель конвективного массопереноса, вызываемого поверхностными эффектами, позволяет достаточно адекватно описать неожиданно быстрый и значительный по величине процесс разделения бинарного расплава на компоненты в тонких капиллярах. Анализ этого явления применительно к каналу с цилиндрической симметрией дает возможность уточнить результаты, отвечающие плоской задаче, и приводит в расчетах к нужному эффекту при более адекватных значениях безразмерных параметров. Тем не менее, по-прежнему, углубленное понимание процессов, которые происходят в приграничных областях расплава, упирается в необходимость более точного экспериментального определения значений некоторых феноменологических параметров рассматриваемой системы.

Работа выполнена при финансовой поддержке РФФИ (проект № 16-01-00662-а).