Sequential Adaptive Fuzzy Inference System Based Intelligent Control of Robot Manipulators

Published Online October 2014 in MECS

Recent years have seen rapid growth in the use of fuzzy controllers to control complex and poorly defined processes. We note that most nonlinear systems are characterized by uncertain parameters, which complicates their control to improve their performance. Especially the model of the robot manipulator is not always available and its parameters are subject to uncertainties caused by friction. These uncertainties often lead to errors and differences of control laws. In this situation is necessary to use the techniques of artificial intelligence.

The Computed Torque Control is an effective motion control strategy for robotic manipulator systems, which can ensure globally asymptotic stability. In this paper, a new approach combining Computed torque control and neuro-Fuzzy (SAFIS) is developed for trajectory tracking problems of robotic manipulator with presence of uncertainty. One solution to this problem is to introduce Neuro-Fuzzy control to ensure the robustness of the controller where the adaptability of fuzzy logic, power learning ability and generalization of neural networks are combined [1]

The neuro-fuzzy networks by their approximation property and adaptation are a major asset to be used in the control law [2],[3]. Several researchers have tried to exploit the advantages of neuro-fuzzy network to control a dynamic system and specifically in the field of robotics [4] .In this paper we use a neuro-fuzzy network Sequential Adaptive Fuzzy Inference System (SAFIS) to develop an adaptive control law of a nonlinear dynamicsystem. It should be noted that SAFIS is a truly sequential on-line learning algorithm for the different parameters of model after we inject into a computed torque control law.

This paper is divided into five sections. Brief description of computed torque control for manipulators is presented in the second section. The Sequential Adaptive Fuzzy Inference Systems (SAFIS) is described in the third section. The proposed SAFIS based control architecture is detailed in section four .The final section is dedicated to simulations. Matlab Simulations are achieved to validate the adaptive approach SAFIS control applied to three degrees of freedom SCARA robot manipulator in a trajectory tracking control, in particular for estimating model parameters of the robot manipulators. The estimated parameters are then injected into control structures.

• II.    C OMPUTED T ORQUE C ONTROL F OR R OBOT M ANIPULATOR

• A.    Dynamic model of robot manipulator

A robot manipulator consists of a mechanical structure, usually a set of rigid bodies connected in series by joints, with an end on the ground, which is the base of the robot, and the end body or effecter’s.[5][16]

The dynamic equation of a manipulator of N degrees of freedom [1] is given by:

Г = M (q )q + C (q , q )q + G (q ) + F (q ) + Г d        (1)

Where Γ is the n×1 vector of actuator joint torque, M(q) is the n×n symmetric positive-definite inertia matrix,

C ( q , q )is the n×1 vector of Coriolis and centrifugal, G(q) is the n×1 vector of gravitational, q , q , q are the joint position, velocity, and acceleration vectors, F ( q )is the n×1 vector of actuator joint friction forces, and n corresponds to the number of degrees of freedom of the robot.

• B.    Computed torque control

The computed torque control [6] is based on compensation for nonlinearities of the robot manipulator. Among the classical control laws of robotic manipulators, the computed torque control is the best in terms of results. Adaptive procedures can be used to compensate the system characteristics not considered in the dynamics modeled, such as those caused by modeling errors and friction. The controller computed torque is shown in Fig.4, is more sophisticated and precise. It uses the technique of feedback, which is to compensate for nonlinearities so that the dynamic system has a linear behavior closed loop. The computed torque control [1] given by:

Г = M (q ) Г о + C (q , q )q + G (q ) + F (q )                (2)

where q_d , q_d and q_d are respectively the vectors of desired position, desired velocity and desired acceleration. Substituting Г in expression (1) and taking into account M ( q ) that is a regular matrix, we have n decoupled linear systems :

q =Г о                                         (3)

where Γ ₀ is an auxiliary input of the select controller. A proportional derivative control ( PD ) is a typical choice for Γ 0 given by the equation:

Г = qd+ Kv(qd - q)+Kp(qd - q)         (4)

• III.    S EQUENTIAL A DAPTIVE F UZZY I NFERENCE S YSTEMS (SAFIS)

• A.    SAFIS description

In this paper, a SAFIS is developed to realize a compact fuzzy system with lesser number of rules. SAFIS uses the idea of functional equivalence between a RBF neural network and a fuzzy inference system [7]. RADIAL BASIS function (RBF) networks offer an efficient mechanism for approximating complex nonlinear mappings from the input–output data. Selection of a learning algorithm for a particular application is dependent on its accuracy and speed [7],[8]. Sequential learning algorithms are better than batch learning algorithms as they do not require retraining whenever a new data is received.

SAFIS uses the Growing And pruning RBF (GAP– RBF) [8]. The SAFIS algorithm consists of two aspects, determination of the fuzzy rules and adjustment of the premise and consequent parameters in fuzzy rules [9].

SAFIS uses the concept of influence of a fuzzy rule to add and remove rules during learning. SAFIS starts with no fuzzy rules and based on the data builds up a compact rule base. The influence of a fuzzy rule is defined as its contribution to the system output in a statistical sense. The parameter adjustment is done using a winner rule strategy where the winner rule is defined as the one Closest to the input data and the parameter update is done using an EKF algorithm.

It should be noted that SAFIS is a truly sequential learning algorithm.

• B.    Radial Basis Function Neural Network

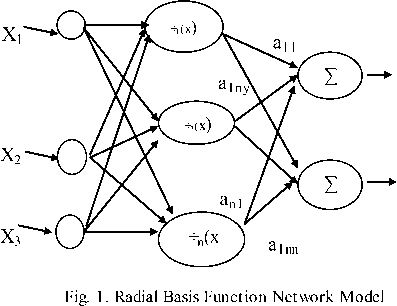
Radial basis function networks are a variety of artificial Neural networks (RBF), it has one hidden layer and a linear output Fig.1, ^y = ^{[ y} _v y 2 ,...., y ny ] which is given by (5):

y = Фт (x) A

The vector A is the weight's vector connecting the hidden layer to the output layer. Ф т ( X) is the response of the hidden layer to the input vector X=[1,x 1 ,x 2 ,…,x nx ) where Ф is the Gaussian function given by [10][15]:

ф ( x ) = exp

a ²

V        7

ц is the center's vector of the hidden neurons and q is the width of the Gaussian functions.

• C.    SAFIS architecture

• 1)    Description of SAFIS architecture

Generally, a wide class of MIMO nonlinear dynamic systems can be represented by the nonlinear discrete model with an input–output description form:

y ⁽ n ) = f ^[ y ⁽ n - ¹⁾, y ⁽ n - ²⁾,..., y ⁽ n - k + 1)

...u ( n ), u ( n - 1), u ( n - p + 1)] k = 1,2,...., N₃ ;

,,  , _h

Where y is a vector containing N_y system outputs, u is a vector for N_u system inputs; f is a nonlinear vector function, k, p are the maximum lags of the output and input, respectively.

[ y ( n - 1), y ( n - 2),..., y ( n - k + 1); u ( n ), u ( n - 1),...

u ⁽ n ^- p + 1)], y (n )                                   (7)

Selecting (5) as the fuzzy system’s input–output x n , y n at time n , the above equation can be put as:

У п = f ( X n )

y Ny yˆ2

y ˆ ₁

a NyN

Layer 1       Layer 2      Layer 3      Layer 4      Layer 5

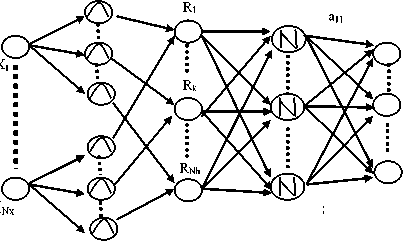
Fig. 2. SAFIS Architecture.

The aim of the SAFIS algorithm is to approximate f such that:

У n = f ⁽ x n )

Where y ˆ is the output of SAFIS. This means that the objective is to minimize the error between the system output and the output of SAFIS, y - y Before describing the details of the algorithm, the structure of SAFIS network is first described below.

The structure of SAFIS illustrated by Fig. 1 consists of five layers to realize the following fuzzy rule model:

Rule k :

if ( x ₁ is A _{1 k} )...( x_NxisA_Nxk ) then ( y ˆ₁ isa _{1 k} )...( y ˆ _Nyisa_Nyk )

Where a jk ( j =1,2…., N y , k =1,2,.., N h ) is a constant consequent parameter in rule k. A ik (i = 1, 2, . . . , Nx ) is the membership value of the i^th input variable x i in rule k. N x is the dimension of the input vector x (x=[x 1 , .. ,x Nx ]^T). N h is the number of fuzzy rules. Ny is the dimension of the output vector У = [ y ... У _Ny f

In SAFIS, the number of fuzzy rules Nh varies. Initially, there is no fuzzy rule and then during learning fuzzy rules are added and removed.[9]

• 1)    Layer 1 : In layer 1, each node represents an input variable and directly transmits the input signal to layer 2.

• 2)    Layer 2 : In this layer, each node represents the m e mbership value of each input variable. SAFIS utilizes the function equivalence between a RBF

network and a FIS and thus it’s antecedent part (if part) in fuzzy rules is achieved by Gaussian functions of the RBF network [11]. The membership value A ik (x i ) of the i^th input variable x i in the k^th Gaussian function is given by

A ik ( X i ) = exp( - ( xi  ^ ⁾² ), k = 1,2,--, N h      (10)

^k where Nh is the number of the Gaussian functions, μik is the center of the kth Gaussian function for the ith input variable, σk is the width of the kth Gaussian function. In SAFIS, the width of all the input variables in the kth Gaussian function is the same.

• 3)    Layer 3: Each node in the layer represents the if part of if–then rules obtained by the sum–product composition and the total number of such rules is N _h . The firing strength (if part) of the k^th rule is given by:

N x

R k ( X ) =П A ik ( X i )

i = 1

= exp( - N X ⁽ x i -^ ik ⁾² )

i = 1      ^ k

= exp( - X - ^ Lt )                 (11)

^ k

• 4)    Layer 4: The nodes in the layer are named as normalized nodes whose number is equal to the number of the nodes in third layer. The k^th normalized node is given by:

  R k

  
  

R k ( X )

N h

E R k ( X )

k = 1

• 5)    Layer 5: Each node in this layer corresponds to an output variable, which is given by the weighted sum of the output of each normalized rule. The system output is calculated by:

EE R k ( X )a_k

=k ^1

y      N h

E R k ( X )

^k =1                                                  (13)

where y = [ У 1 , y 2 ,..., y Ny ] T , a k = [ a 1 k , a 2 k ,..., a Nyk ^{] T}

• 2)    Influence of a fuzzy rule

As in (13), the contribution of the k^th rule to the overall output for an input observation x l is given by:

E ( k , l ) = I a k L R k ⁽ x l )

E R k ( x , )

k = 1

Then the contribution of the k ^th rule to the overall output based on all input data N received so far is obtained by:

S R ( x i )

E ( ^k ) = N N^N----- S S R k ( x i ) k = 1 1 = 1

Dividing the numerator and denominator by N in (14) and using the significance concept of GAP–RBF [4], the influence of the k ^th fuzzy rule is defined as its statistical contribution to the overall output of SAFIS.

Thus, based on [8] the influence of the k ^th rule is given by:

E inf ( k ) = | a _k\ _N ^°^k ) Nx                       (¹⁶)

S (1.8^k )Nx k =1

3) Apply the criterion for adding rules

We proceed by adding a rule if the criterion as in (17) is verified.

I Xn - M nr\ | >  S n and E _inf ( Nh + 1) >  eg     (17)

The parameters of the allocated rule are given by:

a Nh + 1    e n ; ^ Nh + 1    X n

^ Nh + 1 = ^k|| X n - М мД

And then the Fuzzy inference system will contain N h + 1 rules.

4) Parameter adjustment (EKF algorithm)

If the last criterion is not satisfied, the SAFIS will only adjust the actual parameters, SAFIS utilizes a winner rule strategy similar to the work done by [11]. The key idea of the winner rule strategy is that only the parameters related to the selected winner rule are updated by the EKF algorithm in every step [13]. The winner rule is defined as the rule that is closest (in the Euclidean distance sense) to the current input data as in ([12],[8],[14])

The parameters of the allocated rule are given by:

O n = fl O .. O Nh T

= ^{[ a} 1 , Ц 1 , ^ 1 , ....., a nr , ^ nr , ^ nr

•, ^a Nh , ^ Nh , ^G Nh ^]

Where θ nr = [ a nr , μ nr , σ nr ] is the parameter vector of the nearest fuzzy rule and its gradient is derived as follows:

₌ d y n      R n_r

9 a nr   S N = 1 R k

M nr

S y n ^dO nr

_ˆ a nr У n

ENh k=1 Rk

2 R_nr

x n   M' nr

^ nr

.   ₌ ^ y n

^nr dCTnr

a nr - У n

E Nh p k = 1 ^Rk

2 R nr

||xn    M nr II

^ nr

After obtaining the gradient vector of the nearest fuzzy rule B _nr = [ a _nr , / } _nr , СУ _nr ] T , EKF is used to update its parameters as follows:

K n = P n - 1 B n [ R n + B T P n - 1 B n ] ^{- 1}

O n = O n - 1 + K n e n                               (24)

P n = [ I z * z - K n B nT ] P n - 1 + qI z * z                  (25)

where q is a scalar that determines the allowed step in the direction of the gradient vector, Z is the dimension of parameters to be adjusted. When a new rule is added, the dimension of Pn increases to:

( P n - 1 ( 0

0 p 0 I z 1* z 1

Where Z1 is the dimension of the parameters introduced by the newly added rule, p₀ is an initial value of the uncertainty assigned to the newly allocated rule.

5) Pruning the rules

We proceed by adding a rule if the criterion as in (27) is verified

(1.8 ^ nr ) ^Nx   „

^E inf ^{( nr} )   a nr n₄ + 1             <  ^e p

S (1.8^k)Nx k =1

Reduce the dimensionality of EFK

Remove the nr rule, as in (26) [4]

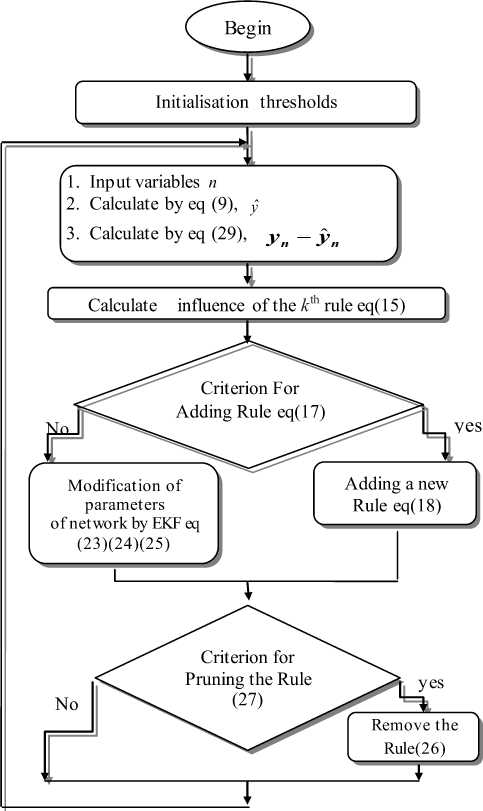
Fig. 3. SAFIS flowchart

D.SAFIS algorithm

The learning algorithm of SAFIS consists of two aspects; determination of fuzzy rules and adjustment of the premise and consequent parameters in fuzzy rules as in Fig.3, SAFIS can automatically add and remove fuzzy rules using ideas similar to GAP–RBF [4] for hidden neurons.

Given the growing and pruning thresholds eg, ep , for each observation ( x n , y n ) , where x_n e R N , y n e R N and n = 1 , 2 ,.. do:

Compute the overall system output given by (13) with

R k ( X n ) = exp( - -1- X n — H k ||²)

Where N_h is the number of fuzzy rules Calculate the parameters required in the growth criterion:

S n = max { ^ _max / ⁿ , ^ m_in } ,  ⁽0 <  / <  1)

e n = У п ^- y n

If the criterion for adding is verified as in (1 7) a new rule is added with new parameters as in (18).

Check the criterion for pruning the rule as in (27), if is verified then remove the nr rule and reduce the dimensionality of EKF. [8][16].

The global SAFIS intelligent control scheme is presented in Fig.4

• V.    S IMULATION R ESULTS

To validate the proposed intelligent control approach, we have carried out simulations for adaptive control of 3 degrees of freedom SCARA robot manipulator whose dynamic model is given by (32, 33, 34,35, 36,)

Due to the complexity of the robot manipulator and its strong non-linearity make using a single network very difficult to achieve. The model matrices (Inertia matrix, Coriolis matrix and friction vector) are estimated using three SAFIS networks.

Before proceeding with the proposed approach, the algorithm parameters needed for the accomplishment of learning are initialized in Table 1.

Table 1. SAFIS initialization parameter

E g (pruning thresholds)	0.001
e p pruning thresholds	0.001
factor of overlap	[1.0,2.0]

..                                 .         .                                                      .

u (1 ) = M (q ) q + C (q , q ) q + G (q ) + f (q ) + 1 1 ( t )    (31)

Where

M_x ! =2.1240 + 1.44cos ( q ₂)

IV. S AFIS B ASED C OMPUTED T ORQUE C ONTROL O F R OBOT M ANIPULATEUR

In this work, SAFIS based control architecture is proposed to overcome the computed torque control lack which is the difficulty to estimate online the model parameters of the robot manipulator, so to compensate uncertainties and noise.

The idea is to estimate the model matrices by a SAFIS networks.

The control law in (2) becomes:

M_x2 = - 0.4907 - 0.72cos ( q ₂)

M =0

M ( q ) = ^ M₂! = - 0.4907 - 0.72 cos ( q ₂)

M₂₂ = - 0.4907, M₂₃ = 0

M = M = M =0

G ₁ =0

G (q ) = ^

G =0

G ₃ = -4.9

Г = M ( q ) Г о + С ( q , q ) q + G ( q ) + F ( q )                (30)

Where ( M , C , F ) is SAFIS estimation of M, C, G and F respectively. The:

^M = ф ⁽q )

C = ^ ([ q , q ])

F = ^ ( q ) G = ^ ( q )

Where 0,p,5,0 are SAFIS network with the outputs q , q .

F (q ) = ^

F =12 q 1 + 0.02 sign (q 1 ) + 3 sin (3 t )

F₂ = 12 q ₂ + 0.02 sign ( q ₂) + 3 sin (3 t )

F ₃ =12 q ₃ + 0.02 sign ( q ₃) + 3 sin (3 t )

5 sin (2 t )

T ( t ) =  5 sin (2 t )

5 sin (2 t )

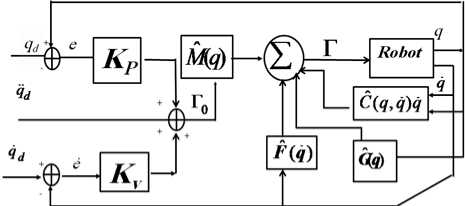
Fig. 4. Bloc diagram of computed torque control with estimation parameters by SAFIS system

Fig. 7. Tracking error position for articulation 3(m)

After having initialized the thresholds of the learning algorithm using table.1 for the three networks SAFIS, we have injected into a computed torque control law of a SCARA robot manipulator with path tracking purpose (q d1 =1.2 Rad, q d2 =1.5 Rad, q d3 =0.1m).

To evaluate the performances of the proposed approach, we will start by using it in an ideal environment (without noise and uncertainties. In the next subsection, we injected some noise in the control loop and have altered the joint masses in the Inertia matrix (∆m 1 =0.002Kg, ∆m 2 =0.001Kg, ∆m 3 =0.001Kg,),

Adaptive control based SAFIS was used to control the robot manipulator with a target of prosecution.

• A. SAFIS Control without uncertainties

In the first step, the SAFIS neuro-fuzzy networks is used to estimate the parameters of the robot manipulator (Matrices M, C and F) without uncertainties parametric.

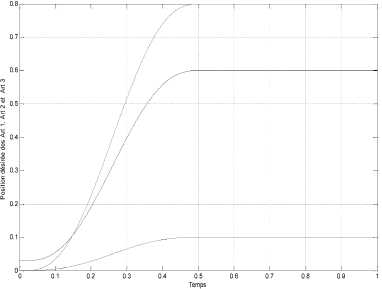
Fig. 5. desired positions

Fig.6 present the position tracking errors for articulations 1 and 2, the third in fig.7

The velocity error for articulation 1and 2 is presented in fig.8, so in fig.9 presented error velocity for the third articulation.

We see that the robot joints converge quickly to the target (0.9 seconds for joints 1 and 2 and 0.01 second for joint 3). These results are obtained thanks to the good estimation of the SAFIS networks and its online learning.

Fig. 6. Tracking error position for articulation 1,2(rad)

B. Simulation with uncertainties and noise

We note that most nonlinear systems are characterized by uncertain parameters, which complicates their control to improve their performance. Especially the model of the robot manipulator is not always available and its parameters are subject to uncertainties caused by friction for example. These uncertainties often lead to errors and differences of control laws.

In this subsection and to test the robustness of the proposed control, we have introduced uncertainties in the parameters of the robot manipulator, where we have altered the components of the inertia matrix (q d1 =1.2 Rad, q d2 =1.5 Rad, q d3 =0.1m).

Fig. 8. Velocity error for articulation 1,2(rad/s)

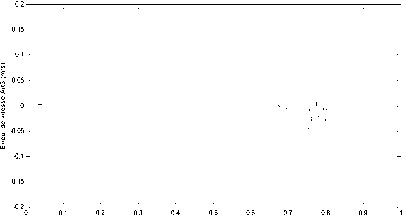
Fig. 9. Velocity error for articulation 3(m/s)

Fig. 10. Tracking error position for articulation 1,2(rad)

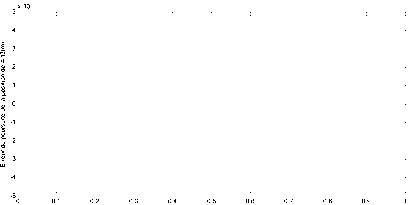
Fig. 11. Tracking error position for articulation 3(m)

In addition to the uncertainties, A white noise is introduced in the control loop.

The position errors are shown in Fig 10, and Fig 11.

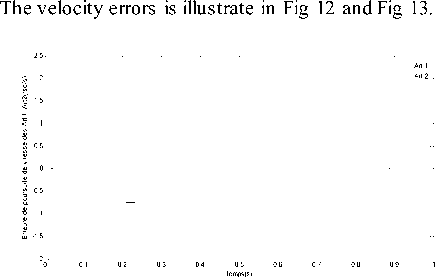
Fig. 12. Velocity error for articulation 1,2(rad/s)

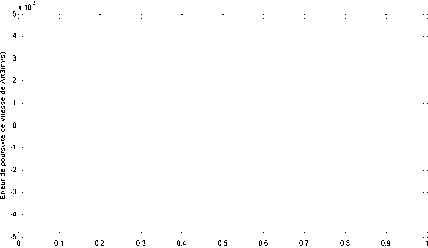
Fig. 13. Velocity error for articulation 3(m/s)

We see that errors are acceptable even a white noise is present and some uncertainties in inertia matrix.

The presence of uncertainties did not affect the control structure performances where they are compensated by the learning power of the SAFIS networks

• VI.    C ONCLUSION

The robot manipulators are often subject to terms of friction and model variation, so it is very hard to get a prior knowledge of their parameters needed by the computed torque control. We presented an online SAFIS based estimation technique of robot model in order to inject it in the correspondent control law. The proposed approach consists of a self adaptive fuzzy inference system of five layers.

In this paper, a sequential fuzzy inference system called SAFIS is developed based on the functional equivalence between a RBF (in this case, GAP–RBF network) and a FIS. In SAFIS, the fuzzy rules are added or removed based on the concept of “influence” of the rule. When there are no additions, only the parameters of the “closest” rule are updated using an EKF scheme. SAFIS is truly a sequential learning algorithm and produces a compact fuzzy inference system.

The performance of SAFIS has been proved with existing of noise and uncertainties on nonlinear systems. The simulations over three degrees of freedom SCARA robot manipulators had given good results in terms of tracking errors even in presence of noise due to the good estimation power of the SAFIS system.