Сеть с симметричной функцией преобразования нейронов для подавления искажений и восстановления изображения

При решении ряда исследовательских и прикладных задач все более широкое применение находят сети с различными видами функции преобразования нейронов. Это — сети с функцией преобразования нейронов, построенной на основе время-частотного распределения (ВЧР) Габора и некоторых других ВЧР (Вигнера—Вилле, кратковременного преобразования Фурье) [1–4].1) В последнее время появляются варианты структуры нейронных сетей с функцией преобразования нейронов, построенной на основе аффинных преобразований (Бертрана и вейвлет [5–8]) и сети с автоподстройкой функции преобразования нейронов (ФПН) [9]. Несмотря на то что для таких сетей получение самих значений ФПН сложнее, чем при традиционном ("сигмоидном")2) виде, при их использовании обычно требуется существенно меньшее количество нейронов и они оказываются более экономичными по числу параметров, подлежащих подстройке в процессе обучения сети. Это особенно важно при ограниченном объеме данных, которые требуется распределять на обучающую и тестирующую выборки.

В полной мере указанные соображения относятся к сетям с симметричной функцией преобразования нейронов (СФПН) [4, 10–12]. Особенность структуры таких нейронных сетей (НС) состоит в локализации элементов скрытого слоя в многомерном векторном пространстве (размер- ность которого идентична размерности входной информации) и в наличии СФПН, зависящей от (метрической) нормы разности векторов локализации элементов скрытого слоя и входного век-тор-сигнала. Сниженное количество параметров, определяющих функционирование сети, сравнительно с другими структурами (при равной размерности данных) обеспечивает сетям с СФПН определенное преимущество при решении задач аппроксимации функций, идентификации и классификации объектов, создании контроллеров.3) Кроме того, оказывается возможным применение сети с СФПН для адаптивного метода снижения шума в многомерном измерительном сигнале и решения задачи восстановления изображения по его измерительному образу, искаженному группой факторов, сопутствующих регистрации.

ПОСТАНОВКА ЗАДАЧИ

При обработке и анализе изображения оно (сравнительно с первичным регистрируемым видом) оказывается искаженным за счет различных причин, среди которых шум (свойственный любому сигналу), элементы интерференции и размытие, вызванное неточной фокусировкой, движением и нелинейностью пленки (при фотографической регистрации).4) В качестве общей модели (в дис- кретном времени) такого "искаженного" изображения могут быть приняты соотношения:

y ( m , n ) = g [ x ( m , n ) ] + n ( m , n ), (1) ^ ^

X ( m , n ) = Z Z- h ( m , n ; k , l ) • s ( k , l ), (2) k =—^ l =—^

n ( m , n ) = f ( X ( m , n ) ) • П '( m , n ) + П "( m , n ), (3) где использованы обозначения: s ( m , n ) — фактическое изображение; ( m , n ) — наблюдаемое (искаженное) изображение; n '( m , n ) и n "( m , n ) — сигналы (процессы) шума; h ( m , n ; k , l ) — импульсный отклик на линейно воздействующее изображение s ( k , l ); g (...) и f (...) — это функции, одна из которых ( g ) представляет характеристики детектора зарегистрированного изображения, а другая ( f ) отражает механизмы формирования шума, связанного с регистрацией изображения. Шум n ( m , n ) моделируется как сумма зависимой от изображения компоненты f ( x ( m , n ) ) x Х П '( m , n ) и независимой от изображения компоненты n "( m , n ).

Метод восстановления изображения включает максимально приближенное к реальности моделирование процессов искажения и применение приближенно обратного процесса к искаженному изображению { y ( m , n ) } , чтобы реконструировать первоначальное фактическое изображение { s ( m , n ) } .⁵⁾ Эффективность метода восстановления изображения зависит от доступности и полноты знания о процессе искажения и от структуры процедур обработки, используемых для получения первичного фактического изображения. После выбора такой структуры и критерия качества реконструкции изображения может осуществляться оптимальная оценка первоначального изображения.

Для восстановления изображения (ВИ) применялись как линейные методы обработки (использующие фильтр Винера или рекурсивный фильтр Калмана [16] и основанные на линейной модели формирования искажений), так и нелинейные методы (метод максимального правдоподобия, или максимальной апостериорной вероятности [17, 18]). Эти методы отличаются друг от друга моделью формирования искажения и набором процедур, ведущих к восстановлению изображения. Однако каждый из этих методов основывается на до- вольно детальном представлении о модели искажения изображения.

Сравнительно недавно для ВИ были использованы нелинейные фильтры, основанные на порядковых статистиках (ПС) и способные подавлять независимый аддитивный импульсный шум. Но относительно искажений, зависящих от изображения, эти фильтры также оказываются неэффективными. Таким образом, традиционное использование как линейных, так и нелинейных методов обработки изображения базируется на корректном и полном представлении о виде модели искажений. Поэтому неадекватность или неполнота представлений о модели (в частности, при зависимости искажений от самого изображения) приводит к неудовлетворительному качеству ВИ.

Утверждение справедливо для различных подходов к ВИ, в том числе для метода, основанного на обучении с использованием образцов изображений. Так, если исходное изображение { s ( k , l )} за счет неизвестного механизма искажения переходит в { y ( k , l )}, то оценка { s ( k , l )} по критерию минимума среднеквадратичной ошибки (МСКО) является оценкой условного среднего. Практически в этом случае часто используется "окно" (2 K +1)(2 L +1) отсчетов искаженного изображения { y ( k , l )}, которое имеет центром пиксель ( m , n ). Оценка s( m , n ) по критерию МСКО с ограничением выражается соотношением:

■$( m , n ) = E ( s ( m , n )| Y_K , L ( m , n ) ) , (4) где⁶⁾

^Y K , L ^{( m} , ⁿ ) = ‘ y ^{( m} - ^k , ⁿ - l )

k = — K , - K + 1,..., K ;

l = — L , — L + 1,..., L

Кроме специального случая, когда сигнал и шум гауссовы и аддитивны, эта оценка является нелинейной функцией от Y KL ( m , n ). Поэтому из-за неполноты знания процессов искажения функционал (4) обычно неизвестен.

Новые возможности решения задачи ВИ открывает использование нейронных сетей (НС). НС способны аппроксимировать нелинейные зависимости сигналов в многомерном. пространстве, обучаться на основе предъявления выборок, отражающих специфику входной информации, и таким образом адаптироваться к виду данных, поступающих на вход НС [19-21]. В частности, при достаточной статистической информации в виде примеров — аналогов изображений НС может быть обучена аппроксимировать нелинейное отображение (4). В этом направлении исследована возможность реализации задачи ВИ с нелинейными вида- ми искажения на основе использования сети с СФПН.

СЕТЬ С СИММЕТРИЧНОЙ ФУНКЦИЕЙ ПРЕОБРАЗОВАНИЯ НЕЙРОНОВ:

ЕЕ ОБУЧЕНИЕ И МОДИФИКАЦИИ

Структура сети с СФПН включает слой входных узлов (с числом, равным размерности входных векторов), скрытый слой с СФПН и выходной слой с линейной ФПН. ⁷⁾ Нейроны с СФП характеризуются (многомерным) вектором своего положения и зависимостью реакции на входное воздействие в виде функции (ФП), зависящей от расстояния (нормы разности) между входным вектором и вектором положения нейрона [11, 12, 22].

■ Сеть размера М (по числу центров с СФПН), принимающая на входе X е R ^{N ex} • и получающая на выходе Y е R ^{М вых} . , выполняет отображение y ( x ): R ^{N ex} . ^ R N^6MX . , согласно соотношению

M

y ^{( x )} = Е w j • й^{|х - c} j || ) ^{,           (5)}

j = 1

где М — число центров с СФПН; ^(...) — нелинейная функция преобразования нейронов (ФПН); ||…|| — символ L2 -нормы; вектор весов выхода сети — wj е RN6MX• (1 < j < M); параметры, называемые центрами сети с СФПН,   — c j е RNex. (1 < j < M).

Наиболее часто в качестве ФПН используется гауссиан — функция f Г ( x ): R N^ex • ^ R N⁶ “ ^x - , которая выполняет отображение

M fГ(x) = Еwj exp(-II x-cj II2 /°2) , j=1

где σ j — параметр, определяющий область определения ФПН (ее "размытие" относительно точки c j ). По сравнению с персептроном сеть с СФПН обучается быстрее, дает лучшее представление о поведении сети при обучении и управлении им, но для задач с размерностью входного пространства N_ex >  10 имеет несколько большее число центров скрытого слоя.

Обучение сети (с настройкой всех ее параметров) осуществляется методом МСКО на основе стохастического градиента (СГ): по входу x n , вы-

ходу y n и желаемому выходу d n на момент n (времени обучения) формируется ошибка e n = d n – y n , и каждая составляющая θ i вектора θ параметров сети подстраивается по алгоритму СГ в соответствии с соотношением

9                _и ^{d || e} n || ²

^в- - 1 " ^в- - ^u д.

,

где u i — скорость обучения для параметра 9 _in (величина u i уменьшается по мере обучения сети).

Параметры сети w j , c j , g j настраиваются в соответствии с соотношениями (7):

^A w j , n = w j , n - 1 ^- w j , n

Act = g — g = j, n        j, n+1        j, n

T

= U ° • e n • w j , n

^{|| x} n ^- c , n ^||2

Ac = с и — c = j , n       j , n + 1       7, n

= U c • e n • w j , n

^{|| x} n ^- c j , n ^||2

g 3

= U w • exp

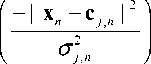
• exp

• exp

- ^{|| x} n ^- c j , n ^||2 2

^{- 11} x n ^- c j , n ^||2 ) 2

Перед обучением производится инициализация параметров:

• — весам { w j , j = 1,2,..., M } придаются малые случайные значения или нули;

― начальное положение центров СФПН определяется как среднее для групп векторов, полученных по алгоритму кластеризации { x i } (из состава обучающей выборки) на М групп;

― для всех ФПН-узлов сети принимается одинаковое значение σ i = σ , равное среднему значению расстояний, которые наиболее близки к выбранным центрам скрытого слоя сети.

• ■ Модификация сети производится путем видоизменения вида ее функций преобразования нейронов (скрытого слоя) с заменой расстояния Фробениуса (т. е. привычной нормы L 2 ) на расстояние Махалонобиса [23]. При этом j -я ФПН φ j представляется в виде

7) Сокращения ФПН, СФП и ФП используются как усеченные варианты СФПН (симметричная функция преобразования нейронов). В процедуре нелинейного представления входного вектор-сигнала ФПН можно трактовать как функцию, порождающую базис.

9 j ^{( x )} = exp *

( xzcJ TE^ j Lt x - cJ

где L j — ковариационная матрица группы { x i } из j -го кластера. Такая форма ФПН позволяет полу-

чить лучшее локальное представление коррелированных входных данных.

Другой тип модификации включает использование нормализации ФПН. Для гауссовой формы ФПН в этом случае выход сети f норм. определяется соотношением

M fнорм(х) = Z w^ орм.(х),            (9)

j = 1

где нормализованная функция преобразования нейронов имеет вид:

exp ( - 1| x - c || 2 / a. ² )

p " ^{opM .}( x ) = MT^------j -----— •     (10)

Z exp ( - II x - C j II ² / a 2 ) j = 1

Сеть с ФПН такого вида имеет несколько лучшие свойства в задачах, связанных с многомерным интерполированием

В расширенной модификации сети, кроме нормализации ФПН по (10), используется смещение векторов {wi} весовых параметров сети на линейно преобразованные расстояния входного вектора x до соответствующих центров ФПН Выход сети, модифицированной таким образом, описывается соотношением норм ;сспс вых .X1

M

= Z l W j + G j • ( x - C j ) | -^орм ^Х       (11)

j = 1 V вых - Х 1 вых -X вх • вх - Х 1     7

где ф**^орм ( x ) определено в (10), { G j } — матрицы размера N_вы х х N_вх , определяющие сплайн-смещение весовых параметров сети { w j }.⁸⁾ Линейное смещение весов, учитывающее степень удаленности входного вектора от центров ФПН, обеспечивает использование информации о градиенте желаемой функции в окрестности каждого центра. (Такая информация не используется не только в основном варианте сети с гауссовой ФПН, но и в ее модификации с нормализованными ФПН). Таким образом, модифицированная сеть с нормализацией ФПН и ССПС имеет преимущества в более совершенной форме представления функций. Для нее применима простая и эффективная форма многомерного алгоритма оптимизации по методу

Ньютона, сеть обучается точно воспроизводить линейное отображение, в то время как сеть в основном варианте позволяет лишь приближенно воспроизводить отображения такого класса.

• ■    Показатели эффективности функционирования НС (обучения, тестирования и точности реализации основной функции сети) должны обеспечиваться не только при аппроксимации детерминированных функций, но и в более сложном случае, когда вход и выход НС связаны стохастической зависимостью. При этом вход x и выход y рассматриваются как реализации случайных векторов X и Y , которые статистически зависимы. Если имеется полное статистическое описание данных, то оценка Y величины Y при заданном только входе X = x может быть получена по критерию МСКО: Y МСКО ( x ) = E( Y | X = x ). В общем случае эта оценка является нелинейной функцией от x, и хотя полное статистическое описание X и Y доступным бывает редко, в большинстве случаев оптимальная оценка может быть вычислена. Чтобы преодолеть недостаток точного знания, принимается некоторая параметрическая статистическая модель и используются данные, чтобы сделать эту модель разумно объясняющей и приводящей в адекватное соответствие совокупность входных и выходных данных (имеющихся в качестве обучающего материала). Такое моделирование затем используется для создания самой обрабатывающей НС. При этом подходе параметры НС приобретают статистическую интерпретацию, отражающую использованное описание данных.⁹⁾

• ■    Описанные выше варианты модификации сетей с СФПН использованы для сопоставления с оценкой сравнительной эффективности восстановления изображений при использовании сетей с различной структурой ФПН. Наиболее адекватной модификацией НС для этой задачи является сеть с ФПН на основе суммы гауссианов. Эта сеть может служить параметрической статистической моделью. НС достаточно проста, а форма ее ФПН ( φ _ΣГ) имеет отчетливую аналитическую трактовку.

Принимается, что вход и выход сети ( X и Y ) принадлежат смеси M групп векторов (соответственно размерности N вх . и N вых. ) с гауссовыми распределениями и при вероятностях A j (j' = 1,^, M) для каждой из групп, т. е. A j = Вер-сть {Данные ( X

TTT и Y) е Группе j}. При этом Zj =( Xj, Yj ) — га- уссов случайный вектор для данных (X и Y), поступающих из группы j; mj и Σj — среднее значение и ковариационная матрица случайного (стохастического) вектора Zj :

где c, = E (X,)’ wj = E (Y,)’

N BX ^{X 1}                 N BMX ^{x 1}

m j

( ⁿbx ^{+ N}вых . ) x ¹

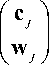
Sx , = E ( X j X T ) - c ,,

N BX. x N BX.

2 - Г £ xj

^{S j} l£^T x , y ,

£ x j y j £ y ,

^У у = ( Ey j x j f = E ( ^X Y T ) ^{- c} , w ^T , N BX. ^{x N}вых .

TT

Sy ,   = ^E ( y , y j ) ^- w j w j .

^Nвых. ^{x N}вых. ⁿb™ ^{x N}вых.

С учетом обозначений (12) у сети, построенной на использовании в структуре суммы гауссианов (1Г), функция ф преобразования нейронов для -го центра выражается соотношением

, ( x ) =

л i^ x j ।^1/2 exp {- 2⁽ x - c , ^)T -⁽ ^j^-1 • ( x - cj }

£ и л lSx k I 1/2 exp I-2 (x - c k )T • (Sx k )-1 • (x- ck)

Символ Σx имеет значение определителя матрицы Σx (см. (12)), например, | A | — определитель матрицы А .

Параметры гауссовой модели (т. е. Л’^, } ’ { cy^ , ^{x , • } , S { y • } ^{и L} { ^x , y , } — все для = 1, 2,…, M ) становятся параметрами анализируемой нелинейной НС. Оценка Y ^ˆ ( x ) по критерию МСКО неизвестного выхода Y при данном только X = x для принятой модели определяется соотношением:

M

^Y ( x ) = £

, = 1

(                                 .-,               .^

w,+ Sx,y,-(Sx,) •(x - cj)

V                  N BX ^X N BX.            7