Сетевые модели и цифровые технологии в повышении квалификации учителей математики

Введение. Особенностями современного образования являются готовность учителей постоянно повышать педагогическое мастерство, осваивать новые образовательные технологии, овладевать новыми компетенциями и др. На наш взгляд, для достижения указанных целей требуется практико-ориентированная система повышения квалификации учителей, по сути, система непрерывного всестороннего развития педагога.

В качестве средства решения этих проблем можно рассматривать индивидуальную образовательную траекторию, которая выступает механизмом самоорганизации и самореализации обучающегося в мотивационном, содержательном, когнитивном и деятельностном аспектах математического образования. Индивидуальная образовательная траектория предполагает создание условий, позволяющих обучающимся:

• -    выбрать объем математического содержания (не ниже базового) и уровень его структу-

• рирования - опорный конспект; интеллект-карта, кейс-метод и т. д.;

• -    выбрать уровни овладения математическим содержанием: адаптивный - помощь и коррекция пробелов); репродуктивный - базовый; творческий - профессионально ориентированный;

• -    использовать темп продвижения по теме, соответствующий своим личностным особенностям;

• -    выбрать формы и вид текущего контроля -тестирование, выполнение самостоятельной или контрольной работы, зачет по теоретическому материалу и т. д.;

• -    выбрать время текущего контроля - в процессе изучения темы, поэтапно, пролонгировано или отсрочено; выбор объема математического содержания определяет его структурирование и визуализацию.

С учетом нынешнего развития цифровых и сетевых технологий для формирования индивидуальной составляющей профессионального образования разумно использовать сетевое взаимодействие коллег.

Целью исследования выступает обоснование и описание использования сетевых моделей и цифровых технологий в системе повышения квалификации педагогических кадров для эффективного формирования индивидуальных траекторий повышения профессионализма учителя математики.

Обзор литературы. Проведя анализ научной и научно-методической литературы, в которой обсуждаются проблемы трансформации современного образования, заключаем, что сегодня традиционные подходы к повышению квалификации учителя требуют переформатирования. В настоящее время сформировались «новые требования к профессионализму педагогических работников» и новые формы «самой системы повышения квалификации» [1, с. 44].

Различные аспекты этой проблемы изучали многие исследователи и педагоги.

Так, Е. В. Евтух отмечает, что в современных условиях «система повышения квалификации педагогических кадров должна переориентироваться с передачи знаний и инновационного опыта в рамках лекционных семинарских занятий на формирование творческих коллективов, решающих реальные педагогические задачи и разрабатывающие реальные педагогические проекты» [1, с. 44]. Далее исследователь рассматривает модель системы повышения квалификации на основе сетевого взаимодействия, в которой, по мнению автора, в более полной мере реализуются особенности настоящей действительности.

• А. И. Рытов в своей работе [2] раскрывает процесс проектирования новой формы повышения квалификации для преподавателей – сетевой модели. Подробно описывает основные функции и этапы формирования модели. Особое внимание уделяется компонентам сетевой образовательной среды.

Л. В. Климбей [3] утверждает, что система повышения квалификации позволяет учителю формировать индивидуальную траекторию и обновлять методологические знания, необходимые для личностного и профессионального роста. Анализу теоретических компонентов становления сетевого профессионального образования как методологической основы формирования кадрового ресурса сетевой (цифровой) российской экономики, информационного общества и обеспечения качества персонализации профессиональных квалификаций разновозрастных групп обучающихся на локальном уровне – уровне крупного сетевого колледжа образовательного комплекса посвящена работа М. В. Никитина [4].

• С. В. Гайсина [5] предлагает рассматривать сетевое сообщество как образовательную технологию, направленную на развитие профессиональной компетентности в сфере реализации педагогического взаимодействия в сетевом пространстве интернета. Выделяет и обосновывает структурные компоненты технологии в процессе формирования сетевых компетенций в системе повышения квалификации. Достаточно много исследований посвящены вопросам моделирования системы повышения квалификации педагогов (ПКП) в целом или анализу отдельных аспектов формируемых моделей. Можно выделить работы T. V. Stashkova, С. В. Савиной, Г. А. Монахова [6–8].

Предпринимаются достаточно успешные попытки формирования теории сетевого образования [9], рассматриваются технологические вопросы реализации сформированных теоретических аспектов [10]. Все это подтверждает целесообразность использования сетевых моде- лей и цифровых технологий в системе повышения квалификации педагогов с целью эффективного формирования индивидуальных траекторий повышения профессионализма.

Методология (материалы и методы). Методологической основой исследования являются идеи субъектно-деятельностного подхода (С. Л. Рубинштейн, А. Н. Леонтьев и др.) и, в том числе, субъектно-средового подхода (С. К. Нартова-Бочавер [11]), которые применяются для формирования сетевой профессиональной среды, направленной на непрерывное повышение профессионального мастерства педагогов.

Также используются идеи по разработке сетевого подхода, сетевой теории организации повышения квалификации. В процессе анализа предметной области определены принципы, лежащие в основе проектируемой модели непрерывного повышения профессионализма учителей математики:

‒ непрерывность совершенствования предметных компетенций учителя математики и педагога дополнительного математического образования;

‒ деятельностно-компетентностный подход при формировании системы непрерывного повышения квалификации педагога-математика;

‒ перевод применения информационнокоммуникационных технологий на уровень формирования и применения сетевых моделей ПКП;

‒ непрерывность функционирования системы непрерывного повышения предметных компетенций.

На наш взгляд, обозначенные принципы в совокупности развивают общие и профессиональные компетенции, необходимые учителям математики.

Приобретение и развитие предметных компетенций при обучении в университете и в процессе прохождения курсов ПК является одним из шагов предлагаемой системы непрерывного повышения предметных компетенций учителя математики или педагога системы дополнительного математического образования (рис. 1). В рассматриваемой модели выполняются транзакции, включающие в себя определенные компоненты развития педагога.

В начале каждой транзакции формируется некоторая обучающая информация о педагоге

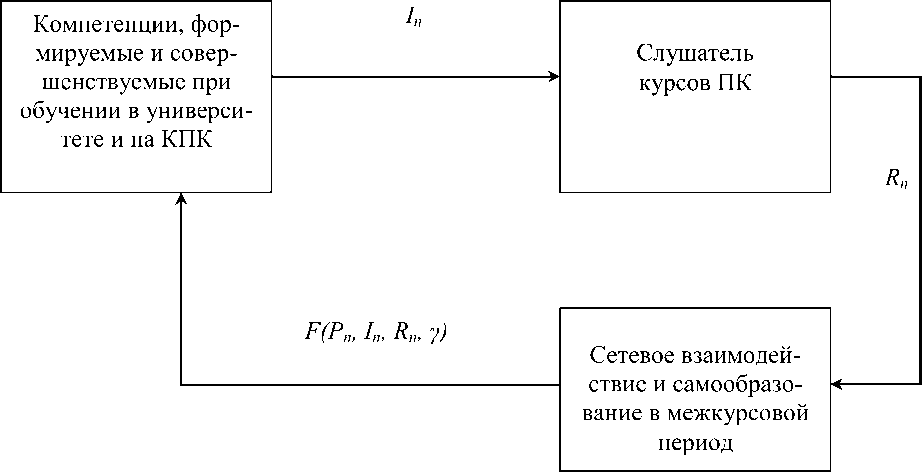
Рис. 1. Модель системы непрерывного повышения предметных компетенций учителя математики или педагога системы дополнительного математического образования

(портфолио), определяемая следующими характеристиками:

, при     , где – номер предметной компе тенции, формируемой или совершенствуемой.

Состояние памяти субъекта на n-м шаге определяется                      массивом:

, компоненты которого       – вероятность отсутствия вла дения i-ой предметной компетенцией на n-й транзакции; при этом вероятность правильного ответа .

задает правильность ответов, значения 0 в случае правильного ответа и 1 – если ответ неверный.

На основе результатов тестирования, модификации портфолио, других данных о педагоге выполняется преобразование матрицы

, где – массив параметров педагога (компетенции определенного уровня, портфолио), а правило преобразования – модель обучения.

После прохождения курсов повышения квалификации в зависимости от значения массива параметров у слушателя формируется аппроксимативная индивидуальная траектория совершенствования предметных компетенций, кото- рая во время реализации компонента «Сетевое взаимодействие и самообразование в межкурсовой период» также может преобразовываться. В процессе каждой транзакции повышается уровень владения педагогом предметными компетенциями, а, соответственно, изменяется массив .

Результаты и их описание. Первый блок предлагаемой модели – «Компетенции, формируемые и совершенствуемые при обучении в университете и на КПК», для реализации которого предлагаются региональные программы курсовой подготовки.

Дополнительная профессиональная программа (программа повышения квалификации, 72 ч.) «Методические аспекты обучения обучающихся математике в современных условиях» разработана преподавателями математики кафедры математики и физики ЛГПУ имени П. П. Семенова-Тян-Шанского.

Цели и задачи программы:

– совершенствование компетенций и повышение профессионального уровня в рамках имеющейся квалификации, необходимых для учителя учреждения общего образования, а также педагога дополнительного образования детей, осуществляющих деятельность в области математического образования;

– формирование систематизированных знаний, умений навыков в области методики обучения различным разделам школьной математики;

– изучение структуры и содержания контрольно-измерительных материалов (КИМ) единого государственного экзамена (ЕГЭ) по математике и основного государственного экзамена (ОГЭ) по математике;

– анализ особенностей основных методов решения задач школьной математики.

Структурно в программу входят модули:

• 1.    Методы решения планиметрических задач. Иллюстрация применения методов в задачах КИМов ОГЭ и ЕГЭ.

• 2.    Методические особенности решения задач теории вероятностей и математической статистики.

• 3.    Технология и методика решения уравнений и неравенств.

• 4.    Прикладные аспекты применения элементов математического анализа в школе.

• 5.    Применение уравнений и их систем к решению различных видов текстовых задач.

• 6.    Оценочный модуль.

Задания для самостоятельной работы разноуровневые и включают структурирование, систематизацию и визуализацию математических понятий и способов действий, профессионально ориентированные задания, в том числе анализ ресурсов по математике, создание методической карты системы заданий из учебников математики и т. д. Слушатели сами выбирают модули, формат (online/offline) и уровень сложности обучения, преподавателя и время занятий. В удобном для себя режиме знакомятся с содержанием модулей, изучают предложенный теоретический материал, рассматривают решения задач и упражнений и выполняют оценочные задания. Программа сфокусирована на формировании готовности слушателей к использованию в своей практике цифровых технологий и успешном освоении приемов и способов овладения инструментами взаимодействия участников образовательного пространства в цифровой среде. Сетевое взаимодействие в рамках повышения квалификации преподавателей математики региона реализуется не только на уровне взаимодействия слушателей курсов ПК, но и, в том числе, вследствие компактности региона, на уровне сетевого сотрудничества образовательных учреждений. В качестве примера кратко охарактеризуем программу совместно реализуемой ГАУДПО Липецкой области «Институт развития образования» и ЛГПУ имени П. П. Семенова-Тян-Шанского. Программа акцентирована на совершенствование предметных компетенций учителей математики в области решения задач различного уровня сложности. Особое внимание при реализации программы обращается на индивидуальную составляющую повышения квалификации. В частности, индивидуализация прохождения курсов реализуется через возможность прохождения нескольких достаточно различных траекторий реализации программы. Траектории реализации программы первоначально формируются на основе предварительного тестирования слушателей и их портфолио, учитываются и предпочтения самого педагога. Курс направлен на совершенствование предметных компетенций преподавателей математики, поэтому первоначально он делится на три раздела: алгебра и начала анализа, планиметрия, теория вероятностей и математическая статистика. В свою очередь каждый раздел достаточно условно делится на уровни: базовый и профильный.

Так как есть возможность выбора различных уровней реализации программы в каждом из разделов, то получаем 23 = 8 траекторий прохождения курса. Каждый раздел включает 4 модуля. Например, раздел «Планиметрия (базовый уровень)» содержит модули «Прикладная геометрия», «Треугольник и его элементы», «Многоугольники» и «Окружность, круг и их элементы». В этом же разделе на профильном уровне модуль «Прикладная геометрия» заменяется на модуль «Теоремы Чевы и Менелая. Барицентрический метод», модифицируется содержание и других модулей. С учетом возможности перехода на другой уровень отдельно для модуля, количество индивидуальных треков прохождения курсов увеличивается до 4 × 23 = 32. Основная часть программы реализуется средствами образовательной платформы и конструктора онлайн-курсов Stepik.org (рис. 2). На очных мероприятиях проводится анализ предметных компетенций, осваиваемых в процессе онлайн-занятий, акцент делается на применение различных методов решения задач. Применению различных методов решения задач предшествует теоретический материал с описанием этих методов и приемов их использования.

Геометрия 7-9 (профильный уровень) Прогресс по курсу: 2/25

2 Многоугольники

Метод центров масс (барицентрический метод)

2.1 Многоугольники Теор.

Будем считать, что

2.2 Параллелограмм

2.3 Трапеция

Материальная точка - это любая пара вида (т, А), где m - некоторое положительное число (масса), А - точка плоскости (пространства). При этом будем допускать запись mA

2.4 Выпуклые многоутоль...

Системой материальных точек назовём любое непустое множество материальных точек (m»A, т^А.. ., тл Ал)

3 Окружность и круг Вли

3.1 Окружность

Для любой такой системы найдётся точка Z пространства такая, что если всю систему произвольным образом в пространстве, а затем «подвесить» ее за нитку в точке Z, то вся система останется в равновесии Эту точку называют центром масс системы материальных точек.

3.2 Вписанные и описанн

Центр масс любой системы материальных точек обладает следующими свойствами

4 Теоремы Чеаы и Менял ..

1 Существование и единственность Любая система материальных точек имеет центр масс, и притом только один

4.1 Барицентрический мет_

4 2 Теоремы Чевы и Мене

2 Однородность Если массу каждой точки системы умножить на одно и то же положительное число к, т е., уменьшить (увеличить) одновременно в одинаковое количество раз, то центр масс не изменится.

О

? ДдааиДй пы^гл Уллламмгя считать что запись тД поползу метает пометённый я точки Д тма малгпй m I 1аитп масс

В частности, анализируются такие основные методы, как геометрический, алгебраический, комбинированный. Также выделяются и иллюстрируются метод опорного элемента, метод введения вспомогательного параметра, метод дополнительных построений, координатный, векторный и векторно-координатный методы.

Вместе с теоретическим и практическим материалом, видеоразбором решений задач, тестовыми заданиями, платформа Stepik.org предоставляет возможности для формирования, так называемых, заданий для рецензирования. Слушатели курсов занимаются взаимопроверкой и рецензированием работ коллег, а преподаватель корректирует эту работу.

Приведем пример задач на рецензирование одного из предлагаемых курсов.

Задача 1. Составьте условие планиметрической задачи с практическим содержанием в стиле задач № 1–5 ОГЭ.

Предусмотрите, чтобы в задаче фигурировал схематичный рисунок школьных помещений, территории Вашей школы, части карты региона, муниципалитета или населенного пункта (выберите один из вариантов).

Спланируйте получение 3–5 ответов.

Предъявите решение вашей задачи.

Задача 2. Дан треугольник ABC. Прямые BA и AC пересекают прямую l, которая параллель- на прямой BC, в точках M и N соответственно. BC = 51, NM = 17. Определите, во сколько раз площадь треугольника ABC больше площади треугольника AMN. Докажите равенство площадей треугольников BAN и CAM. Определите, во сколько раз площадь треугольника BMC больше площади треугольника NMC.

Сформируйте 3–5 подводящих вопросов, упрощающих решение задачи школьниками.

Следовательно, для управления процессом совершенствования педагогами соответствующих предметных компетенций, целесообразно планировать определенную достаточно активную деятельность и в циклах обратной связи. В предложенной модели компонент «Сетевое взаимодействие и самообразование в межкурсовой период» включает в себя следующие основные элементы:

– самообучение и самообразование;

– обсуждение актуальных вопросов на заседаниях методического объединения учителей математики города Липецка, методических объединений муниципалитетов Липецкой области, на дне учителя математики и подобных региональных мероприятиях. Рассматриваемые вопросы коррелируются с тематикой КПК, проводимых в регионе;

– тестирование с целью варьирования программы курсов повышения квалификации, со- вершенствования элементов указанной программы, формирования массива параметров слушателя (портфолио);

• –    сотрудничество педагогического вуза и школы (например, участие учителей в научно-практических конференциях (доклады могут быть связаны с материалом КПК), мастер-классах, месячнике науки, привлечение ведущих педагогов для преподавания в вузе);

• –    методические разработки педагогов обсуждаются в процессе сетевого взаимодействия;

• –    в рамках проведения олимпиады по математике «Уникум», проводится методический семинар для учителей, интересующихся подготовкой математически одаренных детей;

  – взаимодействие школьных учителей, педагогов сотрудников системы дополнительного образования, преподавателей вуза, студентов в организации проектной деятельности школьников.

Компетенции, необходимые современному учителю математики, формируются в рамках получения средне специального или различного уровня высшего образования, разнообразных курсов повышения квалификации, переподготовки, участии в вебинарах, семинарах, тренингах и подобных мероприятиях.

Примеры программ повышения квалификации, проводимых в регионе (курсы ПК как предметной направленности, так и организационной и/или психолого-педагогической направленности):

• –    методические и психолого-педагогические аспекты перехода к ФГОС общего образования при изучении математики;

• –    методика обучения решению планиметрических задач в рамках систематического курса геометрии;

• –    школа современного учителя. Развитие математической грамотности;

• –    система и организация сопровождения учащихся при подготовке к итоговой аттестации;

• – реализация требований обновленных ФГОС НОО, ФГОС ООО в работе учителя;

  – программа профессиональной переподготовки «Менеджмент образовательной организации».

Учителя математики принимают участие и во многих образовательных программах, про- водимых в других регионах. Например, стажировка в рамках июньской математической образовательной программы Образовательного центра «Сириус», «Логика и методы рассуждений в 4–6 классах: методика преподавания и межпредметные связи» Образовательного центра «Сириус».

Внекурсовая деятельность по повышению квалификации включает разнообразные вебинары, семинары, тренинги. Несколько примеров региональных мероприятий указанной направленности: вебинар «Критерии проверки профильного ЕГЭ по математике», семинар «Проектирование внутренней системы методической работы образовательной организации», тренинг по решению заданий для оценки функциональной грамотности обучающихся для учителей математики, образовательный квест для молодых педагогов «Совершенствование педагогического мастерства: приемы и методы развития и формирования функциональной грамотности».

В перечисленных мероприятиях, в частности, рассматривались вопросы применения комбинаторных, вероятностных и геометрических задач, а также их роль в развитии функциональной грамотности в области математики, уделялось внимание актуальным вопросам, связанным с решением ряда заданий Единого государственного экзамена по профильной математике.

Деятельность в рамках курсов ПК и внекур-совое сотрудничество на современном этапе предусматривает активное сетевое взаимодействие всех субъектов системы непрерывного повышения педагогического мастерства, в том числе средствами ИКТ.

Опыт проведенной работы позволяет выделить основные компоненты сетевого взаимодействия субъектов системы непрерывного повышения педагогического мастерства (СНППМ), как в рамках разнообразных курсов повышения квалификации, так и во внекурсо-вой деятельности:

– обсуждение текущих вопросов курсов повышения квалификации;

– объявление о проведении вебинаров, курсов ПК и переподготовки, стажировок, онлайн-лекториев;

– предъявление текстовых, аудио-, видеоматериалов вебинаров, курсов ПК, стажировок, онлайн-лекториев;

– демонстрация методических материалов полезных слушателям курсов ПК (методические разработки уроков, сценарии внеурочных мероприятий, материалы олимпиад, например, муниципального этапа Всероссийской олимпиады школьников по математике, региональных соревнований: олимпиада «Уникум» и «Математические бои» и т. д.;

– обсуждение решений отдельных математических задач;

– анализ подходов к изложению материалов отдельных школьных тем и разделов дополнительной подготовки по математике;

– обсуждение и редактирование методических материалов в рамках работы с Google-документами в облачном пространстве;

– проведение анкетирования по вопросам, связанным с профессиональной деятельностью педагогов;

– формирование статистических данных на основе тестирования субъектов СНППМ;

– обратная связь для определения тематики проводимых мероприятий.

Для организации обратной связи, в частности, применяются разного рода онлайн опросы. Например, на рисунке 4 приведен опрос для выбора темы выступления на дне учителя математики. Предлагаемые варианты: степень точки и радикальная ось в олимпиадных зада- чах, ищем вписанный четырехугольник, применение сервиса geogebra.org для построения планиметрических рисунков, инварианты в задачах с параметрами, также педагоги могут предложить свою тему.

Обсуждение. Основная часть исследования заключалась в анализе некоторых проблем использования сетевых моделей и цифровых технологий в повышении квалификации педагогов. В рамках исследования были выявлены факторы, которые оказывают влияние на выбор педагогами программы повышения квалификации, с помощью анкетирования. В опросе приняли участие 87 учителей математики и педагогов дополнительного образования образовательных учреждений Липецкой области. Участие было анонимным и добровольным. Результаты опроса исследовались с использованием программы STATISTICA. Респондентам предлагалось оценить степень влияния факторов на выбор программы посредством числа от 0 до 10.

В таблице 1 представлены описательные статистики исследуемых переменных.

Корреляционный анализ позволил отметить наличие статистически значимых связей между пунктами анкеты. Направление полученных корреляций согласуется с теорией и практикой образовательного процесса.

Описательные статистики исследуемых переменных

Таблица 1

Фактор	Среднее	Медиана	Стандартное отклонение
Формы обучения (традиционная, дистанционная, смешанная, сетевая)	7,5	8	1,9
Временные затраты	7,7	8	1,8
Привлекательность темы	7,1	7	1,9
Важность для профессиональной деятельности	6,7	7	3
Наличие    творческого элемента	3,5	3,7	2
Возможность формирования персональных треков	7,8	8	1,9
Достижение уровня квалификационных требований	7,4	8	1,7

Анализируя полученные решения, авторы пришли к заключению о необходимости уделять внимание курсам в условиях сетевой модели. Также, на наш взгляд, является полезным некоторый акцент на предметные области, связанные с особенностями региона, вуза.

Заключение. На основе проведенного исследования заключаем, что для формирования индивидуальной составляющей непрерывного повышения уровня педагогического мастерства, в рамках предметной составляющей, целесообразна реализация следующих действий:

– предъявление слушателям КПК возможностей формирования персональных треков прохождения курсовой подготовки;

– предоставление учителям выбора вебинаров, курсов ПК и переподготовки, стажировок, онлайн-лекториев и т. д. благодаря своевременной информации в рамках сетевого взаимодействия;

– обеспечение методическими материалами по интересующей педагогов тематике;

– обмен информацией для своевременной корректировки основных направлений и содержания курсов ПК в процессе реализации предлагаемой сетевой модели.

В дальнейшем планируется развитие приемов формирования и развития вектора параметров слушателя (портфолио) для более полного отражения потребностей субъекта образовательного процесса в совершенствовании предметной подготовки.