Сферически-симметричные решения киральной самогравитирущей модели F(R, (R)2) гравитации в квазиглобальных координатах

В связи с открытием гравитационных волн [1] вызывает интерес процесс их генерации массивными движущимися объектами, в частности - вращающимися двойными системами. К таким

• ¹    E-mail: alexandr308@mail.ru

системам можно отнести двойную чёрную дыру. Динамика такой двойной системы приводит к излучению гравитационных волн, имеющих определённый спектр, который можно регистрировать экспериментально. В этой связи можно поставить вопрос о проявлении каких-либо эффектов и гармоник определённых частот в спектре излучения гравитационных волн, если процесс описывается в рамках модифицированной теории гравитации. Но прежде чем переходить к описанию процесса генерации, следовало бы рассмотреть некоторые модели модифицированной гравитации, получить уравнения этих моделей. В частности, данная работа является подобным шагом, заключающим в себе попытку получения точных решений для модели / (R, (VI?)²) гравитации с целью их дальнейшего анализа.

• 1.    Киральная самогравитирующая модель f (R, (▽R)2) гравитации в сферически-симметричной метрике

В работе [2] рассматривается наиболее общая модель /(R, (VR)2, DR) гравитациии. Частным случаем этой общей модели является модель /(R, (VR)2). Метод преобразования этой модели в гравитацию Эйнштейна со скалярными полями расмотрен подробно в работе [3]. Действие рассматриваемой модели имеет вид:

S ccm = / d%V—/ J ； ^R — 2 严 X,“X," + 4/1(° ) 6^-2 遥 * — 4 фе-^2 " + jX( ( Яе^-^³"g""0,“°,J ,

(1.1)

Здесь /і (ф) ii X(ф) - (1)уііктпш. опреде,「ятоЕ,ііе конкретный вид модели. Рассматривается сферически-симметричная метрика общего вида ds2 = —62"(")必2 + e2M")du2 + е2。® (函2 +sin2(e)dg2).

Метрика пространства целей в соответствии с (1.1) имеет вид ds2 = d%2 — е-^3 "X (ф) dф2.(1.3)

Потенциал модели представлен в следующей форме

爪=W(х, ф) = 4е-^3" (ф — е-，3"/1(ф)) .(1.4)

Поиск решений указанной модели осуществляется в рамках квазиглобальных координат, что со-ответсвует условию:

А = — 〃.

Уравнения Эйнштейна имеют следующий вид

J' + J(20 + 2力=—呂e-2"W,

• —20' — / — J(20 + 2J) — 2(0)2 =呂((%')2 — е-，3"X(ф)(ф')2 + e-2"W) ,

1 + е2"+2。(一/'' — 0 (20 + 2力)=呂e2°W.

Полевые уравнения

%'' + (2〃' + 20) %' — 2ylе-，3"X(ф)(ф')2 = е2"^,

• X (ф)ф''— ^|X (ф)ф'%' +—.J。)(ф')2 + X (ф)(2〃' +20)ф' = —е-2" + ^| %~дф.

• 2.    Решение модели для случая W = 0

В этом случае систему уравнений модели принимает следующий вид

〃“ + J (2/Г + 2〃‘) = 0,

• -20' - 〃‘‘ - z/(20 + 2〃’) - 2(0)2 =呂((О2 - е—^3*Х(0)(“)2) ,

1 + е2"+2。(-/3〃 - /3' (2/3' + 2〃'))= 0.

Полевые уравнения х" + (2〃' + 23') х' - 1Л еҮ ХХ (0)(“)2 = 0,(2.4)

2 Y 3

• Х(О)。" - ^3Х(О)。* +--.：)(。')2 + Х(0)(2〃' + 2/3')。' = ―с-2".

Комбинация уравнений (2.1) и (2.3) приводит к уравнению

〃“ + 3'' + 2(3' + 〃‘ )2 = е-2("+“).

Как видно, в этом уравнении возможна замена переменных следующего вида

〃 =〃 + 3.(2.7)

После такой замены получаем нелинейное дифференциальное уравнение 2 порядка для одной неизвестной функции 〃 (и)

〃 " + 2(т/ )2 = е-2??(2.8)

Найдено решение указанного уравнения, имеющее вид:

〃 =ln д/З — u*)2 — С(2.9)

Это позволяет определить вид зависимости всех метрических функций

〃 =-А = 〃 о +--= ln

⁰  2 К

u — u* — \/С u — u* + %/С

3 = In д/(u — u*)² — С — 〃 0 —

方 *    1

■Сln

u — u* — Сс u — u* + VC

(2.10)

(2.11)

Ведётся поиск полевых функций. В частности, получено уравнение, позволяющее получить зависимость x(u) в явном виде:

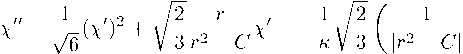
2С -(%)² 、

十( г² - с ) ²   ,

(2.12)

где г = u — u*. Это уравнение получено из (2.2) и (2.4) с учётом известных зависимостей метрических функций (2.10) и (2.11).

Заключение

Решение уравнения (2.12) позволит получить зависимость x(u) и перейти к определению полевой функции 0(u) и функции Х( 。 ). Это является предметом дальнейших изысканий.

В заключение хочу выразить благодарность научному руководителю профессору Червону С.В. за постановку задачи и проявленный интерес к данной работе.