Шестиволновой преобразователь излучения на тепловой нелинейности в схеме с попутными волнами накачки

В системах нелинейной адаптивной оптики для обработки в реальном масштабе времени изображений оптических сигналов могут применяться как четырех-, так и шестиволновые преобразователи излучения [1]. При четырехволновом взаимодействии генерируется волна с обращенным волновым фронтом (ОВФ). При шестиволновом взаимодействии может генерироваться как волна с обращенным волновым фронтом [2–10], так и волна с удвоенным обращенным волновым фронтом [11–14]. В системах адаптивной оптики волна с удвоенным обращенным волновым фронтом может использоваться для компенсации фазовых искажений, возникающих при прохождении излучения, например, через среды с регулярными неоднородностями. При этом оптический путь, который в неоднородной среде проходит сигнальная волна, должен быть в два раза меньше оптического пути, который проходит в неоднородной среде волна с удвоенным обращенным волновым фронтом.

Практическое применение четырех-, шестиволновых преобразователей в системах коррекции фазовых искажений для обработки изображений требует знания того, насколько точно амплитуда волны с обращенным волновым фронтом или с удвоенным обращенным волновым фронтом соответствует амплитуде сигнальной волны. Если вопрос о качестве обращения волнового фронта при четырехволновом взаимодействии в средах с различными механиз- мами нелинейности исследован достаточно подробно [1], то изучению соответствия амплитуды волны с удвоенным обращенным волновым фронтом с амплитудой сигнальной волны уделено недостаточно внимания. Исследована лишь пространственная селективность шестиволновых преобразователей излучения, осуществляющих удвоенное обращение волнового фронта сигнальной волны, на керровской и тепловой нелинейностях в схеме со встречными волнами накачки [13; 14].

Еще одной перспективной схемой для реализации шестиволнового взаимодействия является схема с попутными волнами накачки. В схеме взаимодействия с попутными волнами накачки волна с удвоенным обращенным волновым фронтом распространяется в направлении сигнальной волны.

Представляет несомненный интерес изучение пространственно-временных характеристик шестиволнового преобразователя излучения на тепловой нелинейности в схеме с попутными волнами накачки.

1. Вывод основных выражений, описывающих шестиволновое взаимодействие на тепловой нелинейности в схеме с попутными волнами накачки

Пусть в плоском слое с тепловой нелинейностью толщиной £ попутно распространяются две

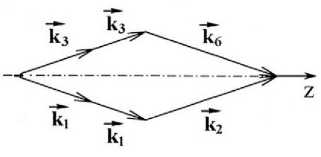
Рис. 1. Схема шестиволнового взаимодействия с попутными волнами накачки

волны накачки с комплексными амплитудами A ₁ и А 2 , частотами © 1 и © 2 , волновыми векторами k i и 1 < 2 и сигнальная волна с комплексной амплитудой A 3 , частотой © 1 , волновым вектором к з . В результате шестиволнового взаимодействия © 1 + © 1 + © 2 - © 1 - © 1 = © 2 генерируется объектная волна с удвоенным обращенным волновым фронтом с комплексной амплитудой A ₆, частотой © 2 , волновым вектором к 6 (рис. 1).

Уравнения Гельмгольца, описывающие распространение и взаимодействие волн на частотах © 1 и © 2 в среде с тепловой нелинейностью, имеют вид [14]:

V2 + к2 + 2k2 dn 5 Т +1 d2n 5 Т2 I - 2 ik1а1 х И           n10 dT    2 dT2 I х (A1,3 + A1,3) = 0, (1) 2 i 2   2 к V2 + к2 + —2 dn 5 Т +1 d-n 5 Т2 - 2ik2а2 х И           n 20 dT    2 dT2 х (A2,6 + A2,6 ) = 0.

Здесь к1,2 = М =©1,2П10,20/ с; П10,20 - средние значения показателя преломления на частотах

– термооптические коэффициенты первого dT ²

и второго порядка соответственно.

Учитывая интерференцию сигнальной волны с первой волной накачки и приближение заданного поля по волнам накачки

(            2                  2 I

И A 1,2| >> | ^А з,б| I,

выражение для интенсивности взаимодействующих волн можно записать следующим образом:

I = I 1 ⁺ I 2 ,

*        *

^где I 1 = A 1 A 1 ⁺ A 1 A 3 ⁺ A 1 A 3 , I 2 = A 2 A 2 .

Уравнения (1) дополняются нестационарным уравнением теплопроводности, описывающим пространственное изменение температуры d5 Т = ^25 T + а111 + а2 I 2 dt              Л Cp v

Здесь Л — коэффициент теплопроводности; C p — удельная теплоемкость; v — объемная плотность вещества.

Изменение температуры можно представить в виде суммы быстро (5Т31) и медленно (5Tq) меняющихся в зависимости от координат состав- ляющих:

5 Т ( r, t ) = 5 T q ( r , t ) + 5 Т з1 (r, t ) + 5 T 1 ( r , t ).

Изменение температуры 5 T q связано с распространением в среде волн накачки, а изменение температуры 5 Т 31 — с интерференцией первой волны накачки с сигнальной волной.

Считаем волны накачки плоскими

A 1,2 ( r , t ) = A 1,2 ( z , t )exp(- ik 1,2 r) .

Комплексные амплитуды сигнальной и объектной волн разложим по плоским волнам:

да

A3,6(r, t) = J A3,6(К3,6, z, t) х -да х exp(-iК3,6P - i^zz)dК3,6.

Здесь A 3б (К 3 6 , z , t ) — пространственные спектры сигнальной и объектной волн; r (p, z ) — радиус-вектор; p — поперечная составляющая радиуса-вектора; К 3 6 и ^к 3 6 _z — поперечные и продольные составляющие волновых векторов ^к 3 6 ; к = к , ।ц = рк 6|.                                                        , ^{1 1 1 1}

Быстро меняющуюся составляющую температуры разложим по гармоническим решеткам:

5 Т31( r, t) = да

= J 5С ? 31 (К т , z , t )exp(- i К т P) d К t ,

-да где 5T31 и Кт — пространственный спектр и про- странственный вектор температурной решетки.

С учетом приближения малого коэффициента преобразования (| A 61² <<  A 3 2 ) выражение для пространственного спектра объектной волны на задней грани нелинейного слоя есть [14]

^            к d n

2 1 ₆(К6, z = / , t ) = - i             2 1 2q ( t ) х

2 n 20 dT ²

t х exp [-C(t, t)] J exp [-i(k2z - k6z)z] х 0

х ^+да5^Г 31 (К₁ т , z , t ) х

-да х 5Т31 (кт = к6 - к2 - К1 т, z, t) dк^dz.

Здесь

C ( t , t) =

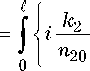
dn s t + 1 d 2 n (5 t ) 2

dT ⁰2 dT ^{2   0}

+ a 2 dz1_,

A2o(t) = A2o(z = 0, t), К2 и kiz — поперечная и продольная составляющая волнового вектора k2 . Выражение (3) получено при условии к6 = 2К 1 + к2 - кз - к3.

При неизменности температуры на гранях не- линейного слоя и выполнении начального условия 5'Тз1(Кt, z, t = 0) = 0 выражение для пространственного спектра температурной решетки имеет вид [15]

да

5 ^T31(K T,z, t) = —7 2 sin(— z)x c Vtt pn

х

х

I t              ^*2

1 J ^A 10⁽ t 1 ) "A 30^{( к} 3 , t 1^)exp { -У n ⁽ t ^- t 1 ) } ^x [ 0

J exp { - i ( k i z - к з z ) z i - 2a i z 1 } x

^L 0

x sin( ⁿ nz 1 ) dz 1

dt 1 -.

Здесь у П = л[(л n /t)² + к T ], A ю( t ) = A ю( z = 0, t ), ^A 30^{( к} 3 , t ) = ^A 30 ^{( к} 3 , ^z = 0, t ).

В стационарном режиме ( t ^ да) при условии неизменности во времени амплитуды первой волны накачки выражение для пространственного спектра температурной решетки есть

5^T31(КT, z) = f [      1       (              А

= -s----;г 1          {exp(-кTz) х в2 - кТ [2sh(кTt1

x [ exp(к т t ) - exp(-0 l ) ] } +                        (5)

⁺ о к ¹    { ^ех Р ^{( к} T z ) [ ^ex P ^{( -e t ) -}

• 2 sh (к т t )

• - ехр(-к т t ) ] } - ехр(-в z ) ^.

Здесь f = |^a 1 ^A_wA 30 (к 3 )] / (Л C p v), в = 2a 1 + i ( k z - ^{- k} 3 z ), ^к T = |^к т | = |^к 1 ^{- к} 3| .

В параксиальном приближении при распространении волн накачки в направлении оси Z имеем

22     22

L.      L.    _ ^к3 - ^к1    7.     Ь    - ^к 6 - ^к2

• k ^{1 z}   k ^{3 z} =   2 k 1    , k ^{2 z   k} 6 ^z =    2 k ₂    .

  

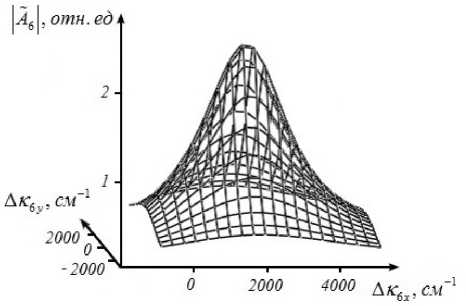
  Рис. 2. Пространственный спектр объектной волны при t = 0.04 с, k 1 = 0.5 k 2 , t = 0.01 см, a 1 = 10 см ^{- 1} , к 1,₂ = + 0.01 k₁₂ , Л = 10 ^{- 4} см ²/ с

  
  
  

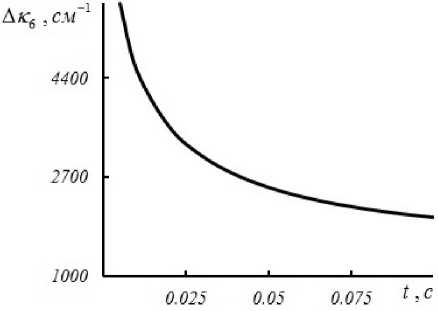
  Рис. 3. Временная зависимость ширины полосы пространственных частот при к = 0.5 к , £ = 0.01, а 1 = 10 см ^{- 1} , к 1,₂ = + 0.01 k 1,₂ , Л = 10 ^{- 4} см ²/ с

  
  

Качество удвоенного обращения волнового фронта обратно пропорционально ширине полосы пространственных частот объектной волны.

С течением времени ширина полосы пространственных частот уменьшается, выходя на стационарное значение (рис. 3). Как и для четырехволнового преобразователя на тепловой нелинейности [15] с ростом коэффициента теплопроводности скорость изменения во времени ширины полосы пространственных частот увеличивается.

Для стационарного режима ( t ^ да) при шестиволновом взаимодействии в схеме с попутными волнами накачки, как и в схеме со встречными волнами накачки [14], ширина полосы пространственных частот объектной волны обратно пропорциональна толщине нелинейного слоя (рис. 4, прямая 1). Изменение соотношения между волновыми числами волн накачки слабо влияет на вид зависимости ширины полосы пространственных частот от обратной толщины нелинейного слоя.

Для сравнения на этом же рисунке приведена зависимость ширины полосы пространственных частот объектной волны (Ак₄) для квазивырож-денного четырехволнового преобразователя излучения к> 1 + ® 2 - to 1 = ® 2 на тепловой нелинейности в схеме с попутными волнами накачки (рис. 4, прямая 2). При расчете использовалось выражение для пространственного спектра волны с обращенным волновым фронтом, взятое из монографии [1]:

/-V

A 4 (к ₄, z = £ )

ik2f dn в2 -кТ^Т

X

I 1

X 5

[ 2 sh (к т £ )

[exp ( -в £ ) - exp ( к т £ ) ] [ к Т + ip ]

x [exp ( -к т £ - ip £ ) - 1] +

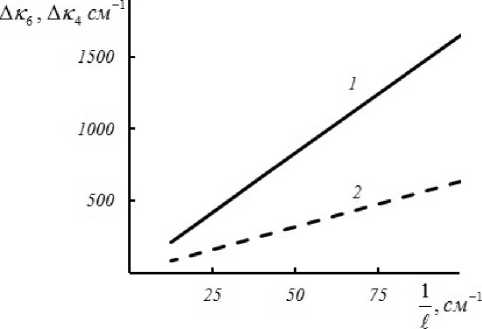
Рис. 4. Зависимость ширины полосы пространственных частот от обратной толщины нелинейного слоя при k = 0.5 k , a 1 = 10 см ^{- 1} , к 1,₂ = + 0.01 k 1,₂

1    [exp ( -в £ ) - exp ( -к т £ ) ]

2 sh (к т £ )          [ к т - ip ]

x [exp ( к т £ - ip £ ) - 1] +

+ [exp ( ^{-в £ -} ip ^£ ) ^- 1]

⁺ в + ip '

Здесь p = k _z - k 4 _z = (к² - к 2 )/2 к 2 . Выражение (6) записано при условии к 4 = к 1 + к 2 - к 3 .

Хотя характер изменения ширин полос пространственных частот от обратной толщины нелинейного слоя как для шестиволнового преобразователя излучения, так и для четырехволно-го преобразователя совпадает, однако ширина полосы пространственных частот для четырехволнового преобразователя излучения примерно в 2.6 раза меньше, чем для шестиволнового преобразователя.

Из (3) с учетом рассчитанных значений ширины полосы пространственных частот объектной волны следует, что входящий в выражение множитель exp [ - i ( k 2 _z - k _{6 z} ) z ] слабо влияет на пространственную селективность шестиволнового преобразователя излучения с попутными волнами накачки. В результате наблюдается слабая зависимость ширины полосы пространственных частот объектной волны от частоты второй волны накачки. Необходимым условием, при котором частота второй волны накачки будет влиять на ширину полосы пространственных частот, является условие ( Ак₆ ) 2 £/ к 2 > 1.

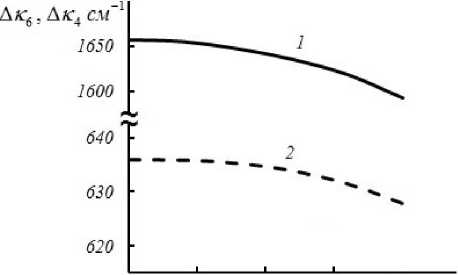
На рис. 5 при условии падения волн накачки на нелинейную среду под одинаковыми углами представлены зависимости ширины полосы пространственных частот от угла падения волн накачки (9 = к / k 1 ) для шестиволнового (рис. 5, кривая 1) и квазивырожденного четырехволно-

О 0.025   0.05   0.075   20 . рад

Рис. 5. Зависимость ширины полосы пространственных частот объектной волны от угла падения волн накачки при k i = 0.5 k 2 , £ = 0.01 см, a = 10 см ¹

вого (рис. 5, кривая 2) преобразователей излучения.

Увеличение угла падения волн накачки на нелинейную среду приводит к уменьшению ширины полосы пространственных частот. Причем при изменении угла падения волн накачки в диапазоне от 0 до 0.04 рад относительные изменения ширин полос четырехволнового и шестиволнового преобразователей излучения равны соответственно 0.7 % и 2.3 %.

Значение ширины полосы пространственных частот в плоскости, перпендикулярной плоскости волн накачки (К 2 К 6 = 0), с точностью ±0.4 % совпадает со значением ширины полосы пространственных частот в плоскости волн накачки.

Заключение

Для шестиволнового преобразователя излучения на тепловой нелинейности в схеме с попутными волнами накачки получена временная зависимость ширины полосы пространственных частот объектной волны с удвоенным обращенным волновым фронтом при использовании сигнальной волны от точечного источника, расположенного на передней грани нелинейного слоя.

Показано, что в стационарном случае ширина полосы пространственных частот волны с удвоенным обращенным волновым фронтом обратно пропорциональна толщине нелинейного слоя , уменьшается с увеличением угла падения волн накачки на нелинейную среду. При сравнении шестиволнового и квазивырожденного четырехволнового преобразователей излучения в схемах с попутными волнами накачки установлено, что характер изменения ширин полос их пространственных частот от обратной толщины нелинейного слоя, угла падения волн накачки совпадает.

Сделаем два замечания.

• 1.    Нелинейный характер связи между комплексными амплитудами объектной и сигнальной волн позволяет по введенной в работе ширине полосы пространственных частот лишь качественно оценивать влияние рассмотренных выше параметров на пространственную селективность шестиволнового преобразователя излучения.

• 2.    Если в выражении (3) для упрощения расчетов перейти от двумерного интеграла по переменным κ_{1 Тх} и κ_{1 Ту} к одномерному, например, по переменной κ_{1 Тх} , то характер зависимости ширины полосы пространственных частот шестиволнового преобразователя излучения от времени, толщины нелинейного слоя, угла падения волн накачки не изменится. Однако абсолютное значение ширины полосы пространственных частот уменьшится. Так, например, при к 1 = 0.5 ^ 2 , « 1 = 10 см 1 , К 12 = + 0.01 k 12 , £ = 0.01 см если от двумерного интеграла перейти к одномерному, то вместо значения ширины полосы пространственных частот 1646 см^-1 получим значение 1260 см^-1.