Щелевые электрозвуковые волны, направляемые поперечно движущейся трещиной пьезоэлектрического кристалла

В серии работ [1–3] нами рассматривалось влияние относительного продольного перемещения (ОПП) пьезоэлектрических кристаллов на распространение электрозвуковых граничных волн в структуре с вакуумным зазором. Именуемые для краткости щелевыми электрозвуковы-ми волнами, они показали изменения дисперсионных характеристик мод под влиянием ОПП, доступные экспериментальному обнаружению даже при низких скоростях относительного перемещения пьезоэлектриков порядка 10-3 м/с [3].

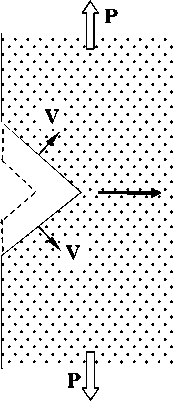
Рис. 1. Схематическая картина трещины, прорастающей с поверхности образца под нагрузкой P

Применительно к структурам со щелью интересно сопоставить результаты, полученные в работах [1–3], результатам, когда зазор (вакуумная щель) между кристаллами, поддерживая распространение электрозвуковых волн, подобно доменным границам сегнетоэлектрика [4; 5] испытывает поперечное перемещение. С чисто формальных позиций объектами такого рода в пьезоэлектрических кристаллах могут выступать плоскостные дефекты типа трещин.

Известно [6; 7], что в динамике движение трещины в твердых телах развивается обычно от ее вершины по касательной к берегам, т. е. трещины удлиняются (прорастают) без ощутимого поперечного перемещения границ. Впрочем, в отдельных ситуациях (прорастание с поверхности под растягивающей нагрузкой P – рис. 1; режим надкритической концентрации напряжений в вершине ветвящейся трещины [6; 7]) поперечная составляющая перемещения границ трещин становится заметной и задача об электрозвуковых волнах на поперечно движущейся трещине пьезоэлектрика обретает физический смысл. Ниже в геометрии, показанной на рис. 2, рассматривается распространение щелевых электрозвуко-вых волн вдоль поперечно перемещающегося по неподвижному кристаллу класса 6mm(4mm, ∞m) вакуумного зазора, который имитирует движущуюся трещину.

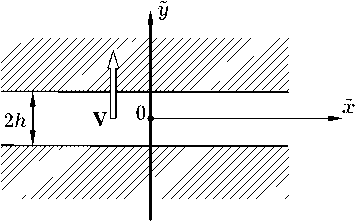
Рис. 2. Геометрия задачи: движущаяся трещина как вакуумный зазор, бегущий по кристаллу

1. Исходные уравнения и граничные условия

Примем, что в попутной системе отсчета Х 0 УZ , привязанной к трещине шириной 2 h , границы трещины У = ± h лежат в кристаллографических плоскостях (010) пьезоэлектрика класса 6mm(4mm, ^m), а оси лабораторной системы отсчета x 0 yz привязаны к кристаллу и соответствуют кристаллографической установке. Примем также, что трещина перемещается в поперечном направлении [ 010 ] II У с дозвуковой скоростью V . Для сдвиговых волн со смещениями u Н z , распространяющимися в плоскости x 0 y , имеем в лабораторной системе отсчета в качестве исходных уравнения [4; 5]

-у- = c_t ²V² и , V²Ф = 0.                         (1)

д t ²

Здесь t — время, V² — оператор Лапласа, c_t = ( c *4 / Р)^1/2 — скорость сдвиговых волн с учетом пьезоэлектрического ужесточения модуля сдвига кристалла с ₄₄ до значения *2

с 4* = с 44 + 4пe / б , e — пьезоэлектрический модуль, Б —диэлектрическая проницаемость, р — плотность. Величина Ф в (1) представляет собой

ницах [4; 5] является правильный отбор ветвей решения при определении зависимости полей смещений и и электрических потенциалов ф, Ф, Ф 0 от поперечной координаты. Из-за непрерывной смены положения границ сделать это возможно только в попутной системе отсчета Х 0 УZ . Данное обстоятельство предопределяет безусловную необходимость построения решения граничной задачи именно в этой системе координат даже в тех случаях, когда единственный интерес представляет поведение решения только в лабораторной системе отсчета.

Для перехода в попутную систему отсчета воспользуемся преобразованием Галилея x = Х , у = У + Vt , z = z , t = f,          (4)

которое адекватно согласуется с принятием ква-зистатического приближения при определении электрических полей. С учетом (4) уравнения (1), (3) примут вид

с

2 t

V2

Ф

^Ф 0

ту часть полного электрического потенциала

*п e    _ ф =---и + Ф ,

Б

которая описывает приграничные электрические колебания, индуцированные под действием акустической волны с границ трещины в кристалл поверхностными пьезоэлектрическими зарядами.

Наряду с электрическими полями приграничных колебаний в пьезоэлектрике необходимо также учитывать электрическое поле потенциала Ф 0 в зазоре | у| <  h . Поэтому уравнения (1), (2) необходимо решать совместно с уравнением Лапласа

V2Ф0 = 0 . (3)

Важным моментом решения граничных задач для электрозвуковых волн на движущихся гра-

д

^ д t

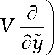
V2

и = 0,

= 0,

V² = ^ + ^. д Х ²    ду

С учетом требования ограниченности потенциалов и смещений из уравнений (5) получим следующее представление решения в попутной си-

стеме отсчета

U 1 = и ( У >  h ) = U 1 exp[ i (ф + к 1 У ) exp(- з/ )],

Ф 1 = Ф( / >  h ) = F 1 exp( i ф) exp(- к/ ),

U 2 = и ( У < - h ) = U 2 exp[ i (Ф + к 1 У ) exp( з/ )],     (6)

^Ф 2 = ^Ф( У / < ^{- h} ) = F 2 exp⁽ i ^ф) ехр^{( к}У / ),

Ф 0 = exp( i ф)[ C exp( k/ ) + D exp(- к/ / )], | У |< h .

В выражениях (6) ф = kx - Q t — фаза колебаний

в волне, отсчитываемая вдоль границ трещины, k – продольная, а

к ₁ =

Q в ct 1 - в2

– поперечная компонента полного волнового вектора k = k + k 1 волны, Q — частота колебаний в попутной системе отсчета, в = V / C t . Величина s , имеющая смысл постоянной амплитудного спадания сдвиговых смещений в пьезоэлектрик от границ трещины, как и в [4; 5] будет определяться равенством

₂ 1 1/2

к ²(1 -в²) -^Q_r    .                   (8)

c t _

³ =-----9

1 -в2

Граничные условия, выражающие при У / = ± h отсутствие сдвиговых напряжений и непрерыв-

ность электрических потенциалов вместе с непрерывностью нормальных компонент электрической индукции, не содержат временных производных и, поэтому, как неоднократно указывалось [4; 5], остаются инвариантными при переходе в попутную систему отсчета. В данном случае, ввиду уравнений пьезоэффекта и с учетом (2), их можно представить в виде

4п e

----u 1,2 + ^ф 1,2

Б

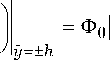
y =± h

дФу дФ0 а г/ г/=± h ay/ г/=± h f * 8ui2    8ф12 )

I c ₄₄---— + e ----— I = 0 .

(     8 y d y J ,

V »             y = ± h

В формулах (9) величинам u и Ф предписывается индекс «1», если соответствующее граничное условие формулируется на верхней границе y = h , и индекс «2» — для условий на нижней границе y = - h .

• 2.    Дисперсионное соотношение и анализ спектра мод

Подстановка выражений (6) в граничные условия (9) приводит к системе однородных алгебраических уравнений, из требования разрешимости которой имеем, в форме равенства нулю детерминанта системы, дисперсионное соотно- шение для электрозвуковых волн на поперечно смещающейся трещине пьезоэлектрического кристалла exp(-2kh)[kK2 - s(1 - б)]2 +

+ exp(-2 kh ) k ² (1 - б )² =

= exp(2 kh )[ k K ² - s (1 + б )]² +

+ exp(2 kh ) k ² (1 + б )² .

Здесь величина K2 = 4ne2 / (бc44) — квадрат коэффициента электромеханической связи пьезо- электрика.

Конфигурацией и принятым характером пере- мещения границ рассматриваемая задача о движущейся трещине пьезоэлектрика напоминает рассмотренную в [8; 9] задачу для электрозву-ковых волн на движущемся полосовом домене сегнетоэлектрического кристалла. Именно этим объясняется идентичность выражения (10) дисперсионному соотношению работ [8; 9], если не обращать внимания на поле упругих смещений внутри полосового домена. Соответственно сразу можно заключить о принадлежности волн на трещине к разряду неколлинеарных электрозву-ковых волн со всеми их особенностями, отмечавшимися в [4–9].

Сравниваемые задачи, тем не менее, не сводятся друг к другу из-за очевидных отличий в граничных условиях. Проистекающие отсюда различия в дисперсионных свойствах электро-звуковых волн, удерживаемых движущимся полосовым доменом и движущейся трещиной, составляют необходимый элемент новизны для последующего анализа.

Движение трещины сказывается в (10) присутствием вторых слагаемых, пропорциональных k ² . При k ^ = 0 в частности имеем вместо (10)

exp(-2 kh )[ k K ² - s (1 - б )]² = = exp(2 kh )[ k K ² - s (1 + б )]² .

Обе стороны этого равенства образуют полные квадраты, что позволяет сразу понизить порядок уравнения вдвое, прибегнув к процедуре извлечения корней:

exp(- kh )[ k K ² - s (1 - б )] = = ± exp( kh )[ k K ² - s (1 + б )] .

Наличие двух корней отражает существование двух независимых ветвей спектра мод электро-звуковых волн. Группируя в (11) члены при K ² и s получим соответственно

K ² =o[1 + Б cth(^)], K ² =o[1 + Б th(^)], (12)

где £ = kh, ст = sh. В выражениях (12) нетрудно разглядеть дисперсионные соотношения симметричной и антисимметричной моды щелевой электрозвуковой волны для случая неподвижных кристаллов без поперечного пьезоэффекта и фиксированного зазора [3].

Если в (10) сгруппировать члены, пропорциональные k2 в правой стороне равенства, то в условиях движения трещины получим

{ K ² - СТ[1 + Б th©]}{ K ² - СТ[1 + Б cth(^)]} = ₍₁₃₎ = - p ²[1 + Б ctg(^)][1 + Б th<^)].

Сравнение выражений (12) с выражением (13), где p = k ^ h , показывает, что движение трещины обеспечивает параметрическую связь мод щелевых волн, меняющую вид спектров. Для предельно тонкой трещины с ^ 0 на основании (13) имеем квадратное по s уравнение: s ² - sk K ² + k ² = 0. Оно предсказывает в результате движения трещины снижение коэффициента граничной локализации колебаний антисимметричной моды s ® k K ² - k ² / ( k K ²) и,

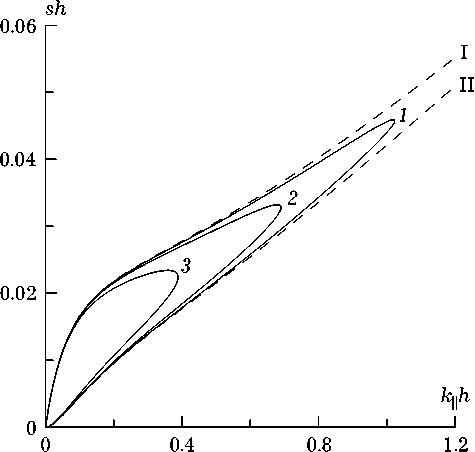
Рис. 3. Спектральные зависимости локализации щелевой электрозвуковой волны поперечно движущейся трещиной пьезоэлектрического кристалла: 1 — в = 0.01; 2 — в = 0.02;

3 — в = 0.04

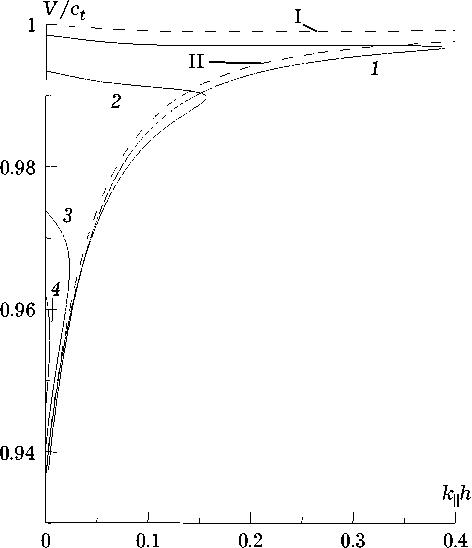
Рис. 4. Дисперсионные спектры щелевой электрозвуковой волны на поперечно смещающейся трещине: 1 — в = 0.04; 2 - p = 0.08; 3 - p = 0.15; 4 - p = 0.17

напротив, возникновение и пропорциональное повышение граничной локализации колебаний симметричной моды s ® k ² / ( к К 2 ).

В другом предельном случае с ^ м уравнение (13) не имеет решения, если p ^ 0. Этот результат объясняется тем, что в условиях движения трещины для стационарного (вещественного, например, положительного к > 0) распространения неколлинеарной электрозвуковой волны необходимо, чтобы поток энергии в волне, подтекающий с одной стороны трещины ( y < - h ), уравновешивался потоком энергии, отводимой волной с другой ее стороны ( y >  h ). Указанный баланс потоков регулируется сцеплением электрических полей через трещину и, естественно, возможен только при достаточной малости тол-

щины трещины, что находит отражение в существовании верхней границы решения уравнения (13): ^<^ max .

Уравнение (13) должно рассматриваться совместно с равенствами (7), (8) из которых следует, что к ² = Р 2 [ к 2 (1 -в²)^-1 - s 2 ]. С учетом этого соотношения уравнение (13) можно предста-

вить как квадратное по ст уравнение

ст

-

K ²

1 -р2

f ©ст +

' K ^{2 v} . 1 — в²,

g © = 0

с функциями

f © = [1 + £ th(^)]^-1 + [1 + £ cth(^)]^-1,

g © = - + K ⁴

1 -p2

[1 + £ th(^)][1 + £ cth(^)]

.

При выполнении условия f 2© > 4 g © оно парой своих корней Ст 12 >0 задает аналитически зависимости ст = ст© спектра коэффициентов граничной локализации мод щелевых электро-звуковых волн на берегах поперечно движущейся трещины. Процедура расчета сводится, таким образом, к подстановке найденных значений s для заданного k в формулы (7), (8) и поочередном вычислении величин Q и к ^ . Типичные результаты расчетов представлены на рис. 3 и 4 для случая, когда пьезоэлектрик характери- 2

зуется параметрами K = 0.35, £ = 7, а трещина имеет низкую скорость поперечного перемещения в << 1.

Штриховые кривые, обозначенные на рис. 3, 4 римскими цифрами I и II, п редставляют соответственно зависимости в случае неподвижной трещины (в = 0) для антисимметричной и симметричной мод электрозвуковой волны, спектры которых даются выражениями (12). Видно, что движение трещины становится причиной параметрической связи симметричной и антисимметричной мод, которые при в ^ 0 не существуют изолированно друг от друга.

Вследствие указанной гибридизации спектров электрозвуковая волна на движущейся трещине приобретает смешенные признаки симметрии/ анти-симметрии распределения потенциала электрического поля поперек зазора. Анало-

гичную асимметрию в распределение упругих смещений граничной электрозвуковой волны поперек полосового домена в сегнетоэлектрике вносит, как было показано в [8; 9], движение полосового домена. Однако в этом случае изолированность мод движением полосового домена не нарушалась – спектры электрозвуковой волны трансформировались движением домена без гибридизации.

Геометрически гибридизация мод электро-звуковой волны выражается смыканием ветвей спектров ее локализации (рис. 3) в замкнутую петлю и образованием дисперсионных спектров (рис. 4) в форме полупетель. Подобные особенности преобразования поверхностных и граничных волн движением границ отмечались ранее для сред с подсистемами резонансного типа [10–12]. Применительно к движущейся трещине пьезоэлектрика резонансные качества в форме оптимизируемой связи кристаллов полями через зазор (трещину) демонстрирует уже не среды сами по себе, а слагаемые ими слоистая структура.

С ростом скорости поперечного движения трещины происходит заметное укорачивание петель спектра локализации электрозвуковой волны. Дисперсионные полупетли зависимостей фазовой скорости электрозвуковой волны в попутной системе отсчета v (Ω) = Ω/( k ² + k ² _⊥ )^1/2 от волновой толщины трещины kh (рис. 4) при этом выпрямляются и укорачиваются.

Связь фазовых скоростей v(Ω) и v(ω) электро-звуковой волны, а также других ее характеристик в попутной и лабораторной системе отсчета, вытекает из общих уравнений пьезоакустики (1). По этой причине относительность спектрального представления электрозвуковой волны для движущейся трещины будет такой же, как и в случае движущихся доменных границ [4; 5; 8; 9]. В частности, имеем v(ω) = v(Ω)(1 -β2), откуда следует, что полная делокализации колебаний в пределе β→1, когда петли спектра локализации электрозвуковой волны на рис. 3 стягиваются в начало (sh → 0, kh → 0), сопровождается «остановкой» электрозвуковой волны: v(ω) →0. Детальное объяснение этого феномена было дано в [9] для случая полосового домена и может быть целиком перенесено на рассматриваемый случай движущейся трещины. Именно, замечая, что в пределе β→1 трещина приобретает нулевую толщину, а волновая нормаль полностью ориентируется по направлению движения трещины, этот результат объясняется расцеплением волны с трещиной.

Работа выполнена по гранту РФФИ в рам^ ках проекта № 14-07-00621.