Сходимость процессов Лагранжа - Штурма - Лиувилля для непрерывных функций ограниченной вариации

В отличие от подхода Крамера [1], положившего начало изучению аппроксимативных свойств лагранжевых операторов с узлами интерполирования в собственных значениях задачи Штурма — Лиувилля, Г. И. Натансон в [2] получил признак Дини — Липшица равномерной сходимости внутри интервала (0, п), т. е. равномерной на любом компакте, содержащемся в (0, п), процессов Лагранжа — Штурма — Лиувилля вида

Д           и_(x)Д

LSLU» = 52 f (xk,»)"^---W-------7 = 52 f (хк,п)1кП(х)"Д!)

k=1        Un(xk,n)(x — xk,n)   ^=1

Где Un есть n-ая собственная функция регулярной задачи Штурма — Лиувилля 'U" + [А - q]U = 0,

< U ‘(0) - hU (0)=0,                                (1.2)

_U ‘(п) + HU (п) = 0

Свойства операторов интерполирования функций вида (1.1) тесно переплетаются с поведением так называемых синк-приближений кп \   у\ (—1)k sin nXf n /        nx — кп k=0

n

Ln(f,x) = £

sin (nx

k=0

nx

^кп) _f kπ

^^^^^^^^r

^^^^^^^^r

т)-    »”

используемых в теореме отсчетов Уиттекера — Котельникова — Шеннона (см. [3-6]). Оператор (1.3) представляет собой оператор (1.1), построенный по собственным функциям задачи Штурма — Лиувилля (1.3), в случае нулевого потенциала и краевых условий первого рода. Достаточно подробный обзор результатов, полученных в области исследования свойств синк-аппроксимаций (1.3) аналитических на действительной оси функции, экспоненциально убывающих на бесконечности, а также наиболее важные приложения синк-аппроксимаций можно найти, например, в [5].

Синк-приближения активно используются при построении различных численных методов математической физики и приближения функций как одной так и нескольких переменных [6-25] в теории квадратурных и кубатурных формул [5] и всплесков или теории вейвлет-преобразований [3, 4, 6].

До появления работ [11, 12, 14, 16-19, 22] приближение такими операторами на отрезке или ограниченном интервале осуществлялось только для некоторых классов аналитических функций (см., например, [5]) сведением к случаю оси с помощью конформного отображения. В [19] получена оценка сверху наилучшего приближения непрерывных функций комбинациями синков.

В [20] установлено, что при попытке приближения негладких непрерывных функций значениями операторов (1.3) возможно появление резонанса, приводящего к неограниченному росту погрешности аппроксимации на всем интервале (0, п). В [21-25] предложены различные модификации синк-приближений (1.3), позволяющие аппроксимировать непрерывные функции на отрезке [0, п]. Исследование полноты системы синков (1.3) в [24] в пространствах C [0,п] 11 Co[0,п] = {f : f G C [0,п], f(0) = f(п) = 0} позволяет сделать вывод о бесполезности попыток построить сумматорный оператор из синков, допускающий возможность равномерной аппроксимации произвольной непрерывной функции на отрезке.

Изучение операторов Лагранжа — Штурма — Лиувилля (1.1) также тесно связано с исследованием аппроксимативных свойств операторов интерполирования, построенных по решениям задач Коши с линейными дифференциальными выражениями второго порядка [26]. Операторы, предложенные в [26], являются обобщением операторов Лагранжа — Штурма — Лиувилля (1.1) и классических синк-приближений (1.3) одновременно. В [27] приводятся некоторые приложения результатов работы [26] к исследованию аппроксимативных свойств классических алгебраических интерполяционных многочленов Лагранжа с матрицей узлов интерполирования, каждая строка которой состоит из нулей многочленов Якоби Р“^п,вп с параметрами. зависящими от n.

Изучению различных свойств операторов Лагранжа — Штурма — Лиувилля (1.1) посвящены также работы [28-34]. В работе [31] устанавливается существование непрерывной на [0, п] функции, интерполяционный процесс Лагранжа — Штурма — Лиувилля (1.1) которой неограниченно расходится почти всюду на [0, п]. Исследования, проведенные в [28-30], показывают, что задача представления непрерывной функции как предела значений операторов (1.1) некорректна по Адамару.

В монографии [34] приведены более подробные доказательства и исправлены опечатки, обнаруженные в некоторых формулах более ранних публикаций.

В настоящей работе, используя концепции исследований в [35-42], установлена равномерная внутри интервала (a, b) сходимость интерполяционных процессов (1.1), построенных по решениям задачи Штурма — Лиувилля (1.2) для непрерывных на [0, п] и имеющих ограниченное изменение на [a, b] функций f.

В этой работе будем считать потенциал q задачи Штурма — Лиувилля (1.2) непрерывной функцией с ограниченным изменением на [0, п]. Пусть также каждая собственная функция будет удовлетворять условию нормировки Un(0) = 1. Рассматриваем краевые условия (1.2) третьего рода, из которых исключены условия первого рода, т. е. h = ±от, H = ±то. Для .ттобых 0 С a < b С п. 0 < e < (b — a)/2 нищлесы p1, p2, mi 11 m2 определим с помощью соотношений xP1,n С a + E < xpi + 1,n,

xP2,n ^{С b E}< xp2 + 1,ni

xkl- 1,n < a ^С xki,n,   xk2 + 1,n ^С b <  xk2+2,n,

(1.4)

m1 = [y] ⁺ 1,

m² = [kr]

после добавления к множеству нулей X1,n < x2,n < • • • < xn,n n-ой собственной функции Un то чек xo,n = 0 и xn+1,n = п. Здесь [z] обозначает целуто часть числа z. Если не оговорено иное, штрих у суммы в этой работе будет означать отсутствие слагаемого со знаменателем, равным нулю.

Модуль непрерывности функции f G C[0, п] обозначим, как обычно,

w(f,5) =    sup    |f (x + h) — f (x)|.

|h|<5;

x,x+hG[G,n]

Будем называть модулем изменения функции f на от резке [a, b] функцию натурального аргумента n-1

v(n,f) = suP ^|f (tk+1) — f (tk)|>

Tn k=G где Tn = {a С to < t1 < t2 < • • • < tn-1 < tn С b}. n G N. Заметим, что функция f является функцией ограниченной вариации на отрезке [a, b], т. е. f G V[a, b], если существует константа Mf такая, что для любого натурального n справедливо неравенство v(n,f) С Mf.

Теорема 1.1. Пусть 0 С a < b С п, 0 < E < (b — a)/2. Для любой функции f G C[0, п] П V[a, b] выполняется соотношение lim ||f - LSLf OHc^+yb-e] = 0, n→∞

(1.5)

где оператор Лагранжа — Штурма — Лиувилля LSL(f, •) определен в (1.1).

Замечание 1.1. При этом на множестве [0, п] \ [a, b] соотношение lim |f (x) - LSL(f,x)| = 0

n→∞ может вовсе не выполняться (см., например, [28, 31, 34]).

• 2.    Вспомогательные утверждения

Прежде чем доказывать эту теорему убедимся в справедливости ряда вспомогательных утверждений.

Лемма 2.1. Пусть U_n — собственная функция, соответствующая собственному значению X_n, регулярной задачи Штурма — Лиувилля (1.2). Через 0 < xi,n < x2,n < • • • < x_n,_n<  п обозначим нули функции U_n. Тогда имеют место следующие асимптотические формулы:

U_n (x) = cos nx + sin nx + O(n

Un^(x) =

^Un^(x) =

n

—n sin nx + e(x) cos nx + O(n

2),

1),

—n² cos nx — ne(x) sin nx + O(1),

Un (xk,n) = (-1)k n + O(n

1),

xk,n =

2k —

2n

1            2k - 1

-п + n 2в (   2 n п ) + O(n

3),

1),

(2.1)

(2-2)

(2-3)

(2-4)

(2.5)

(2.6)

где

x

e(x) = -cx + h + 2 j q(T) dr, c = П ^h + H + 2 jn q(T) dr^ , а оценка остаточного члена во всех формулах (2.1)—(2.5) равномерна по x Е [0, п] пли 1 ^ k ^ n.

• <1 По поводу доказательства (2.1), (2.2) и (2.6) смотрите, например, [44]. Убедимся в справедливости (2.5). Пусть xp_n — k-ый нуль собственной функции U_n. Из асимптотической формулы (2.1) получаем соотношение

  cos nxkn +

  
  

e(xk,n)

= O(n 2).

------sin nxkn

n

Положив cos ak,n :=

n

Vn2+e2(Xfc,n)

получим асимптотическую формулу

sin (1 + nxk,n — ak,n^

= O(n 2).

Следовательно, имеем соотношение |П + nxpn — ak,n — пk| = O(n 2). Но функция в, по крайней мере, один раз непрерывно дифференцируема, поэтому имеет место асимптоти ческая формула

xk,n =

2k —

2n

—п + n ² в

2k — 1

(.'■+ O(n ).

Формула (2.3) следует из (2.1) и (1.2), а (2.4) — из (2.2) и (2.5). >

ЗАМЕЧАНИЕ 2.1. Из асимптотической формулы (2.1) видно, что выбранная нормировка собственных функций Un обеспечивает их ограниченность в совокупности. Обозначим

M = sup{|Un(x)| : x G [0,n],n 6 N} < то, (2.7)

Пусть p\ = o(|П^) щaii A ^ +то. Считаем, что 3iтачепия функции h(X) G R для произвольного неотрицательного X. Обозначим через qA произвольную функцию из шара VPA [0, п] радиуса ра в пространстве функций ограниченной вариации, исчезающих в нуле, т. е.

Vo" Ы < РА,  РА = o (|nX) ’

X ^ то, qA(0) = 0.

(2.8)

Для произвольного потенциала qA G VPA [0, п] при X ^ +то нули решения задачи Коши

Г у’’+ (X - qA(x)) у = 0,

(2.9)

(2.Ю)

(2.П)

( y(0,X) = 1, y‘(0,X) = h(X), или, при дополнительном условии h(X) = 0

Vonы < РА, ра = o(|nX), X ^ то, qA(0) = 0, h(X) = 0, задачи Коши

( у’’ + (X - qA(x))y = 0,

( y(0,X)=0, y‘(0,X) = h(X), попадающих в отрезок [0, п], пронумеруем следующим образом:

0 < xo,А < x1,A < ... < xn(A),A < п  (x-1,A < 0,   xn(A)+1,A > п)-

(Здесь x—i,A < 0, х_п(а)+1,а > п обозначают нули какого-либо продолжения решения задачи Коши (2.9) или (2.11) при сохранении ограниченности вариации потенциала qA вис [0, п]). В [2G. 34] описано множество непрерывных па отрезке [0, п] фуикипи f. допускающих равномерную внутри интервала (0, п) аппроксимацию значениями операторов следующего вида. Определим оператор, построенный по решениям задачи Коши (2.9) или (2.11), ставящий в соответствие каждой конечнозначной на множестве {xk,A}n=o _n=1 непрерывную функцию по правилу

SA^(f, ^x) = V ,₍                 з ^{f (x}k,A) = V sk,A^{(x)f (}xk,A).          (2.12)

k=0 y (xk,A,X)(x xk,A)            k=o

Очевидно, что значение оператора (2.12) интерполирует функцию f в узлах {xk,A}n=o-

Обозначим Co[0, п] = {f : f G C[0, п], f (0) = f (п) = 0}. При приближении с помощью операторов (1.1) функций f G C[0, п] \ Co [0, п] вблизи концов отрезка [0, п] возникает явление Гиббса (см., например, [21, теорема 2], [34]). Заметим, что эта проблема решается с помощью обобщения оператора (2.12), предложенного в [26, формула (1.9)], [34], вида т A      y(x,X)      J,, x   f (п) - f (0)            1 , f (п) - f (0)

^{Ta(/ )} £ У‘(хк,А)(х — Xk,A) V ^{( Л)}       *     ^ ^f(0)/⁺     ,     x ^{+ f(0)}'

где y(x, X) — решение задачи Ко ши (2.9) или (2.11) и Xk,A — нули этого решения.

В следующей лемме выделяется главная часть погрешности аппроксимации функций f G Co[0,п] с помощью операторов вида (2.12).

Лемма 2.2 [26, предложение 9], [34]. Пусть y(x, X) — решение задачи Коши (2.9) или (2.11), и предположим, что в случае задачи Коши (2.9) выполняются условия (2.8), а в случае задачи Коши (2.11) — условия (2.10). Если f G Cg[0, п], то равномерно на [0, п] справедливо соотношение lim λ→∞

f ^(x) - SA^(f,x)

-

n—1

J2( f ^(xk+i,A) - f^(xk,X⁾ sk,A^(x) k=0

)

= 0.

(2.13)

Далее, нам потребуются следующие утверждения.

Лемма 2.3. Пусть Un — собственная функция, соответствующая собственному значению Xn, регулярной задачи Штурма — Лиувилля (1.2). Тогда существует константа Ci. зависящая только от q, h, H, такая, что для всех x G [0, п] и всех n = 1, 2, 3,... справед ливо неравенство

|lSL;(x)| =

Un(x) n^(xk,n^{)(x    x}k,n

С Ci.

(2.14)

• < 1 Если для каких либо 1 С k С пип G N окажется x = xpn, то |l^Sn(x)| = 1-Рассмотрим теперь случай x = xpn. Пусть сначала 0 < |x — Xk,_n| С п^—i, x G [0,п]. Тогда по формуле Тейлора с остаточным членом в форме Лагранжа из (2.3) и (2.4) следует неравенство

  ^|lSn^{(x)| С}

  
  

  Un^(xk,n^{)(x   x}k,n) + Un ⁽€k,n^{)(x   x}k,n) /²

  
  

  U_n (x_k,n )(x

  
  

  ^^^^^^^^

  
  

  xk,n)

  
  

  O(n²)    1

  = 1+-- \, -И- n + O(n ⁱ) n

  
  

  С Ci,i

  
  

для некоторой константы Ci,i, выбор которой зависит только от параметров задачи Штурма — Лиувилля q, h и H. Осталось расемотреть случай |x — xk,_n| >  n^—i, x G [0, п]. В силу асимптотических формул (2.1) и (2.4) существует константа Ci,2, для которой справедливо неравенство

|lS,n(x)|

С п

Un(x) Un (xk,n)

С

cos nx + e(xx) sin nx + O(n 2) n + O(n—i)

n С Ci,2.

Положив Ci = max(Ci,i, Ci,2), убедимся в справедливости леммы 2.3. >

Лемма 2.4. Существуют константа C2 и но мер ng G N, не зависящие от функции f G C[0, п]. 0 С a < b С п Iт0 <  е < (b — a)/2 такие, что для произвольных x G [a + E,b — е] и n > ng справедливо неравенство

• 2      ^      |(^f(xk+i,n) ^{— f (x}k,n⁾)lS,n^(x)| ^С C2^ (^f,n) ^ln ^E-        (2.15)

ke[i,n— i]\[ki,k2]

< Введем обозначение

^k,n = f (xk+i,n) — f (xk,n), 1 С k С n — 1; n G N.               (2.16)

Учитывая, что f G C[0, п] и (2.5), убедимся, что существует константа C3 такая, что справедлива оценка

|^k,n| С C3^(f,n), 1 С k С n — 1; n G N.                   (2.17)

Возьмем произвольное x G [a+е, b — е]. Сумму в (2.15) представим в виде двух слагаемых, каждое из которых оценим следующим образом:

( ki-1              n—1

E |С ^(х)| + E |С ^(х)1

k=1            k=k2+1

Воспользовавшись (2.2), (2.4) и формулой конечных приращений Лагранжа, продолжим оценку суммы в (2.15) следующим образом:

е   щ,,.&)|« cf ) jUnx)¹ (е ¹

kE[1,n—1]\[ki,k2]                                                 V k=1

^|x xk,n

n

+ E k=k2+1

^|x   xk,n

)

₊ CJfL ^{)    E}            ___IUn(x)L

• ³    ,n kE[1,n— 1\[ki,k2] ^n(xkn^x - xkn   n^|X - xkn

=.,.⁾jUnixn fE ¹    ■    . E         ) +^-1).

\ ^— J ^—   \^k= |x ^— xknj   k=2₊₁ ^{|x —} xk,n|           nJ

Из асимптотической формулы (2.5) для нулей собственных функций Un находим номер —о, выбор которого зависит только от параметров задачи Штурма — Лиувилля, начиная с которого будет выполняться неравенство

15™—1 |xk+1’n xk’n| ^ 2—"                            I2"18'

В силу того, что max_xG(o,_n) { ln |x(n — x)|} = 2ln 2, infln ⁿ ^ ln2, (2.7) и (2.18) сумму в (2.15) равномерно на всем отрезке [а + е,Ь — е] можно оценить таким образом:

ke[1,n—1]\[ki,k2]

X

k1—1 E k=1

xk+1,n — xk,n

xk+1,n

/ x xk,n

dt

— t

n—1

+ E k=k2+1

xk,n

— xk—1,n

xk,n         x

Г dt

J t — x xk- 1,n

⁺ " ( f-n ) ^O(-—*>⁵ (4CM ⁺ Щ[^O(-—1)) ^ln7" ( ^f-n ) '

(2.19)

Откуда следует существование константы C2, выбор которой зависит только от параметров задачи Штурма — Лиувилля (1.2). >

Для любых 0 5 а < b 5 п. 0 < е < (b — а)/2 обозначим

Qn(f, [a,b],e):= max E ‘ f (x^m+^n) — f (x2"'1 pi5p5p2 ‘-^          p — 2m m=m1

Лемма 2.5. Если функция f G C[0,п], то из соотношения llim Qn(f,[а,ь],е) = 0 λ→∞

(2.20)

(2.21)

следует утверждение (1.5).

<1 Заметим. что из (2.16). (2.2) и (2.4) вытекает равномерная на. веем отрезке [0,п] оценка.

k2                                               k2

52 ( ^f (xk+1,n) - fЫ) l^x) - 52 ^kn k=ki                                      k=ki

(-1)^k Un(x) n(x - Xk,n)

k2

< 52 |^k,n| k=ki

Un(x) ^(x xk,n⁾

^Н) ‘ , n - U n ( x k, ) = f'

nUn (xk,n)         V п

(2.22)

Положив в случае задачи Коши (2.9) h(A) = h, A = An, г де An — собственное значение задачи Штурма — Лиувилля (1.2), получим тождество Un(x) = y(x,An). Следовательно, значения операторов (1.1) и (2.12) при A = An тождественно совпадают. Из (2.15), леммы 2.2 в случае задачи Коши (2.9) A = An и (2.22) получаем соотношение lim n→∞

( f (x)

- LSL(f,x)

-

n -1

2 E( f (Xk+in)

k=0

-

f(xkn^lkUx^

= lim n→∞

-

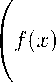
₁ k 2

Ln^L(f,x) - 2 52 ^n k=ki

(-1)^k Un (x) n(x - Xk,n)

= 0.

(2.23)

Выберем и зафиксируем некоторое x G [a + е,Ь - е]. Найдем индекс p = p(x,A), для которого выполняется соотношение x G [xp,n, xp+pn). Toгда x = xp,n + a(xp+1,n - xp,n), где a = a(x, A) G [0,1). ii x x = p - k + a + вк,п П k,n n .

Из (2.17) и (2.5) одновременно для всех x G [a + е, b - е] и настолько больших n, что для всех 1 ^ k ^ n - 1 имеет место неравенство |вк,_п | < 1, справедлива оценка

Е

k: k 1 ^k^k<2 ; |p-k|^3

^(-1)k ^k,n p ^- k ^{+ a + e}k,n

- k:k1 ^k^k2;

|p-k|^3

^(-1)k ^k,n p-k

< Cs^(f,ⁿ)   ^   ।---- .... ^a ..   _ < 3Ca^(f,ⁿ).    (2.24)

^{V   П)} k:k^k₂; |P - ^k|(|P - ^k|- ^{2)          V} n⁷

|p-k|^3

Учитывая обозначение (2.16) разобьем сумму в (2.23) на. два. слагаемых

12                                              1                                 1

2 52 f (xk+1,n) - f (xkny) lkLn(x) = 2   52   ^k,nlkLn(x) + 2   52   ^k,nlkLn(x)- <2-2y> k=k1                                                  k:ki

|p-k|^3                               |p-k|<3

Следовательно, из неравенства, треугольника, (2.14), (2.16), (2.17), (2.23) и (2.24) имеем равномерную по x G [a + е, b - е] опенку

₁k2

2 52 (^{f (}xk+1,n) - ^{f (x}k,n⁾)l^SL)^{(x) -}k=k1

Un(x) 2п

k2

Е k=k1

^(-1)k^k,n p-k

= o(1).

(2.26)

Из (2.26) и (2.23) также равномерно по x G [a + e,b — е] вытекает соотношение lim n→∞

f (x) — LSL(f,x) —

Un(x) 2п

k2

E k=ki

^(—l^)k ^k,n p — k

= 0.

(2.27)

Оценим последнее слагаемое в соотношении (2.27), используя (2.1), (2.7), (2.17) и неравенство треугольника,

Un^{(x) у2}' ‘ ^{( —1)k}^k,n  < 2 M V² ‘I ^2m,n I + M у²' ‘I ^k,n I + о

(4f,n)y (22S)

2п "^ p — k 2п "^ I p — 2m I 2п '^ I p — k I k=k1                    m=mi                k=k1

Можно подобрать последовательность натуральных чисел {ln}n=i, удовлетворяющую свойствам:

ln = o(n),   lim ln = то,   lim ш n→∞       λ→∞

ln

(f-n)E 1 = 0.

k=1

(2.29)

Оценим вторую сумму в (2.28) следующим образом:

¹У"' ‘I ^к,^п I

2п I p — k I k=k1

¹    ^^ ‘I ^k,n I + ¹    ^^ ‘I ^k,n I

2п           ^Ip — k^I 2п           ^Ip — k^I

k:|p-k|ln

(2.30)

Из неравенства (2.17) для достаточно больших n следует оценка

¹            ‘I ^k'ⁿ I <  ¹            ‘I ^k'ⁿ I < C3  ⁽f ^{П) у}^ ¹

2п          ^Ip — k 1^ 2п ^Ip — k 1^ п   \ , nJ k

k:|p-k|

(2.31)

Вторая сумма в (2.30) после преобразования Абеля в случае k G [ki, k2] : |p — k| > ln может быть оценена следующим образом

1 2П

Е

k:|p-k|>l

‘I ^kn

^Ip — k n

4hf IIC[a,b]                у 1

<  l„ + 1  +4|f IC[a,b] E k(k+I) .

k=ln

Отсюда, из (2.29), (2.30) и (2.31) равномерно по x G [a + e,b — е] получаем асимптотическую формулу

M ^E ‘Iyk^nI = _о(1).

(2.32)

2п ^—* I p — k I k=k1

Теперь из (2.27), (2.28), (2.32) и неравенства треугольника получаем оценку

If (x) — LSL(f,x)I < ^MMQn(f, [a, b], е) + o(1).

Следовательно, из выполнения условия (2.21) следует равномерная сходимость (1.5). >

• 3. Равномерная сходимость интерполяционных процессов Лагранжа — Штурма — Лиувилля внутри интервала (a, b)

Убедимся в справедливости утверждения сформулированной ранее теоремы 1.1.

• <1 ДОКАЗАТЕЛЬСТВО ТЕОРЕМЫ 1.1. В силу непрерывности функции f на отрезке [0, п]. для любого п<оложителыюго e существуют патуральные числа v ii n такие, что для всех n > n (n Е N) одновременно справедливы два соотношения

fA E1

k=1

24 |f Ilc[a,b] < ev.                                            (3.2)

Пусть n > ni. Найдем индекс po, зависящий от n, a, b, e и f на котором достигается максимум в определении (2.20), т. е.

Q*„(f, МЫ = ^ ‘ f(x2”*"1 — f '    • z—'        pn — 2m m=mi

Обозначим

k2 ‘ f (xk+1,n)   f (xk,n)

Po — k

Q"*(f, [a,b],e) := £ k=k1

Так как Q"*(f, [a, b], e) получается из Q"(f, [a, b], e) добавлением неотрицательных слагаемых, то для любого натурального n справедливо неравенство

Q"(f, [a,b],e) ^ Q"*(f, [a,b],e).                                (3.3)

Разобьем Q"*(f, [a, b],e) на два слагаемых

Q"-(f, M.e) = E 'fx^p^fx^ k=k1          ^{|Po    k|}

^^^^^^^^.

„ V^ ‘‘ f (xk+1,n) — f (xk,")

(3.4)

2 >    -------,------r.-------= Si(po) + S2(po), k=k1         |po - k| где два штриха означают, что в сумме неотрицательных слагаемых и слагаемого с индексом k = pg iic'T.

Сначала займемся оценкой первой суммы. Для чего представим ее в виде

Si(po) =

k:kG [^1,^2] ’ 0< |p0-k|

f (Xk+1,n) — f (Xk,n) |po ^{— k|}

+

E

k:kG[ki,k2"], |P0^-k|^^v

f (Xk+1,n) — f (Xk,n) |Po ^{— k|}

= S1,1(po) + S1,2(po).

(3.5)

В случае {k : k Е [k1, k2], 0 < |po — k| ^ v} = 0 считаем второе слагаемое равным нулю.

Из неравенства (3.1) для всех n > ni имеем соотношение

|W|< 2.f n) f k < |. k=i

(3.6)

Теперь оценим Si,2(po)- Echii для po имеют место перавеиетва po — ki ^ v ii k2 — Po ^ v. то используем (3.2) и с помощью преобразования Абеля получим оценку

|Si,2(Po)|

С

С

P0-V f k=ki

f (xk+i,n)   f (xk,n)

Po — k

+

k2 f k=Po+v

^f(xk+lvn)   ^{f (x}k,n)

k — Po

f 1       4lfIIC[a,b]

^4f »C[a,4Xi(i+T)⁺ ---V--- i=v

8|f llc[a,b]      6

С v < 3 ‘

(3.7)

Таким образом, из (3.5), (3.6) и (3.7) для всех n ^ ni имеем оценку

ISi(po)| С |.                                        (ЗС)

Перейдем к изучению свойств суммы S2(po) Возьмем произвольное натуральное m : 1 С m С k2 — ki — 2 и пред ставим S2 (po) в виде двух слагаемых

S2^(po) = ^—2Г

k:ke[ki,k2]> |P0-k|^m

‘‘ f (Xk+i,n) — f (Xk,n)

|po — k|

^^^^^^^^.

E

k:ke[ki,k2]> |p0-k| >m

‘‘ f (Xk+i,n) — f (Xk,n)

|po — k|

= S2,i(po) + S2,2(po)-

(3.9)

Выберем достаточно большой номер n ^ ni, зависящий только от параметров задачи Штурма — Лиувилля, начиная с которого, в силу (2.5), будут выполняться неравенства mаX1ckcn |xk+i,n—Xk,n| С |n- Функция f G C[0,п], начиная с n2 будем иметь соотношение

|f(xk+i,n) — f(xk,n)| С 10Kfш

f,πn.

(3.10)

Поэтому, с I I о            ‘‘ |f (xk+i,n) — f (xk,n)|                  ПА 1

• S²,^{i (p}»⁾ = ²  E -----..   .-----^{С 10K}f“V-n)Ek.     '„ш

k:k£[ki,k2],                 ^o                                                k=i

|P0-k|

Далее оценим сумму S2,2(po):

P0—m—i 0 С S2,2(po) С 2 f k=ki

— (f(xk+i,n) — f (xk,n)) — po — k

k2

+ 2 f k=p0+m+i

(f (xk+Цп)   f (xk,n)) —

(3.12)

k — po где z- = z Jz1. Ес ли po — m С ki и ли po + m > k2, то в (3.12) исчезает соответственно первое или второе слагаемое. В случае po — m < k1 < k2 < po + m сумма S2,2(po) в (3.9) вообще отсутствует. Учитывая то, что f G V[a, b], с помощью преобразования Абеля и (3.10) оценим (3.12)

k2-k1-1

v (k,f) k²

+ 1°K; of).

0 С S2,2(po) С 4Mf £ k=m+1

Отсюда (3.9), (3.11) и (3.12) имеем о с W с 10K,f\ Е     у 1 v(f +i0Kf f).

k=1         k=m+1

Положив при каждом п ^ п₂m := ln, выбранное как в (2.29), получим, что в силу ограниченности последовательности {v(k, f )}//=₁ и сходимости ряда ^2^=1 v(k, f )/k² существует номер пз G N, пз ^ п₂, такой, что для произвольного п ^ пз справедливо неравенство

ǫ 0 < S2(po) < з.

Отсюда и из (3.3), (3.4), (3.5), (3.8) получаем, что для произвольного е > 0 можно найти номер пз G N такой. чт<> для веек п > пз будут справедл! 1вы неравенства. Qn(f, [a, b],e) С Q"(f, [a,bU) < е. Теорема 1.1 доказана. >