Сильная согласованность в задачах восстановления зависимостей по интервальным данным

Задача восстановления зависимостей - это популярная и практически важная задача, в которой по эмпирическим данным требуется построить зависимость заданного вида между «входными» и «выходными» величинами. Далее в работе мы рассматриваем простейшую зависимость вида b = а1 x1 + a2x2 + ...+ anxn,                                     (1)

в которой значения b являются линейной функцией от независимых переменных а 1 , а ₂, .. , a n . Необходимо определить неизвестные коэффициенты x i , чтобы получившаяся зависимость «наилучшим образом» соответствовала заданному набору значений a i и b , полученному в результате m измерений (наблюдений)

0 (1 , а 2 ¹ ) ,..., а^¹, b ⁽¹⁾,

а ( ²⁾, а 2 ²⁾, ..., а     b ⁽²⁾,                                                (2)

...

а ( ^m ) , а 2 ^m ) ,..., а П^m ) , b ^{( m} )

(верхние индексы в скобках означают номер измерения). Нередко эту постановку называют также задачей оценивания параметров объекта или задачей идентификации.

Подставляя данные (2) в равенство (1), после переобозначения а_у : = а j ) и b i : = b ^{( 1} ) получаем систему уравнений относительно x 1 , x ₂, . , x n :

• ^а11 x 1 ^{+ а} 12 x 2 ⁺ ... ^{+ а} 1 n x n = ^b1 ,

• ^а 21 ^x 1 + ^а 22 X 2 ⁺ ... ^{+ а} 2 n x n = ^b 2 ,

...             . ..             ...

• ^am1 ^x 1 ^{+ a}m 2 x 2 ⁺ "^{. + a}mn^Xn = ^bm , или, кратко,

Ax = b с m х n -матрицей A = ( а^) и m -вектором b = (bi). Её решение, обычное или в обобщённом смысле, принимается за оценку параметров x1, x2 , . , xn . Наглядная графическая иллюстрация задачи восстановления зависимости показана на рис. 1: требуется найти прямую, проходящую через начало координат, которая «наилучшим образом» приближает множество точек с координатами (2).

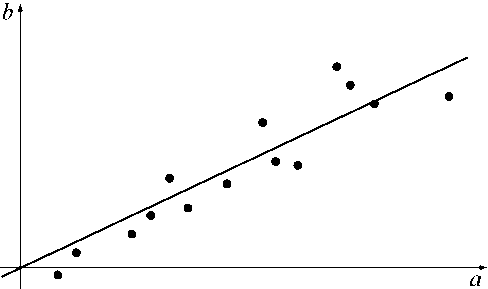
Рис. 1. Иллюстрация задачи восстановления линейной зависимости: точки – это данные измерений, по которым необходимо построить функцию заданного вида, «наиболее точно» приближающую их

Но в практических задачах восстановления зависимостей данные почти всегда неточны, поскольку на результаты измерений влияют внешние неконтролируемые факторы, сами измерительные приборы не являются абсолютно точными т. д. и т. п. Таким образом, реально мы должны иметь дело с той или иной неопределённостью – состоянием частичного знания об измеряемой величине, когда нам известно какое-то её значение, но оно приближённое, и имеется также некоторая информация (качественная и количественная) о погрешности этого значения.

Как описывать эти погрешности? Иными словами, какую «модель неопределённости» данных мы принимаем? Традиционный выбор – это теоретико-вероятностная модель ошибок, основы которой заложили на рубеже XVIII и XIX веков К.Ф. Гаусс и П.С. Лаплас. Согласно этому подходу ошибки измерений и наблюдений являются случайными величинами, адекватно описываемыми математическим аппаратом теории вероятностей, и нам (более-менее) известны характеристики этих случайных величин. Теоретико-вероятностная модель ошибок за прошедшие два века получила очень большое развитие и популярность, сделавшись основным инструментом обработки данных. Тем не менее, её приложение вызывает необходимость ответа на многие нетривиальные вопросы, и эти ответы подчас не вполне удовлетворительны.

Ниже мы конспективно перечислим некоторые из проблем, возникающих при применении теоретико-вероятностных методов в статистике. Наш короткий обзор естественно дополняет работы [1, 2], где есть подробное обсуждение проблем и трудностей теоретико-вероятностной статистики.

Статистическая устойчивость. Прежде всего, мы должны принимать во внимание тот факт, что в основе самого понятия вероятности лежит так называемая частотная интерпретация, при которой вероятность того или иного события понимается как отношение числа благоприятных исходов к общему числу исходов рассматриваемого явления (эксперимента и т.п.), либо близкая к ней конструкция. Несмотря на то, что в современной теории вероятностей, построенной на аксиоматике А.Н. Колмогорова, математическая вероятность определяется как некоторая специальная мера на множестве событий, она формализует именно частотное понимание вероятности. Наконец, именно частотная интерпретация вероятности является основой всех приложений теории вероятностей к практике (см., к примеру, [3]). Существование подобной частоты, как объективной характеристики реальных явлений и процессов, является фундаментом самого существования теории вероятностей и залогом её успешного применения к моделированию окружающего нас мира.

Но важно осознавать, что эта модель не универсальна, она является определённой идеализацией, имеющей свою сферу применимости, весьма широкую, но всё-таки ограниченную. Многие явления окружающего нас мира, в отношении которых вполне применим общепринятый термин «случайные», не обладают свойством существования устойчивой частоты, так как при росте числа наблюдений эта относительная частота не устанавливается, а имеет тенденцию к постоянным колебаниям [4]. Для описания и анализа подобных явлений традиционная теория вероятностей непригодна.

Свойство существования относительной частоты событий называется статистической устойчивостью (статистической однородностью), и часто теорию вероятностей определяют как «математическую теорию статистически устойчивых явлений» (так делается, к примеру, в классической книге [5]).

Так или иначе, если нет статистической устойчивости, теоретико-вероятностные конструкции напрямую применять к решению задачи нельзя. В этом случае и традиционная математическая статистика, основанная на теории вероятностей, также не может служить подходящим инструментом для обработки данных.

Проблема малых выборок. Теоретико-вероятностные закономерности проявляются как тенденции, которые наиболее ярко видны для массовых явлений. При малом или небольшим количестве испытаний выводы теории вероятностей могут оказаться весьма далёкими от истинной картины явления. «Проблема малых выборок» — это вопрос о том, достаточен ли объём выборки (количество измерений и т. п.) для того, чтобы выводы, получаемые на основе теоретиковероятностной модели ошибок, имели приемлемую практическую достоверность. Связанный с этим вопрос: какие методы следует применять для обработки выборок, являющихся «малыми», где теория вероятностей не способна адекватно описать поведение погрешностей?

Неизвестные вероятностные характеристики распределения. Каков конкретный вид распределения погрешностей? Каковы его числовые характеристики? Имеют ли данные корреляцию между собой? Или же они независимы? Многие классические результаты теоретиковероятностной статистики требуют, как известно, независимости рассматриваемых случайных величин либо заданного уровня корреляции. Проверка этих условий на практике представляется почти невозможной.

«Робастность» модели обработки данных. Под этим требованием понимается адекватная устойчивость оценок, получаемых на основе тех или иных моделей, к малым возмущениям в данных, т. е. к вероятностным характеристикам распределений и их форме. Некоторые вероятностно-статистические методы не обладают этим свойством, давая ответы, чувствительность которых к возмущениям в данных неразумно велика.

Удобство вычислительных методов. Насколько удобны и практичны вычислительные технологии для решения соответствующих задач статистики? Некоторые традиционные методы теоретико-вероятностной статистики удовлетворяют этому условию. Например, широчайшее распространение метода наименьших квадратов в задачах обработки данных обусловлено, помимо ясного теоретико-вероятностного смысла, также его удобной вычислительной схемой: в линейном случае решение задачи наименьших квадратов сводится к решению системы линейных алгебраических уравнений. Но в более сложных ситуациях методы теоретико-вероятностной статистики технологической простотой уже не обладают (например, тот же самый метод наименьших квадратов в нелинейном случае). Это повышает «конкурентоспособность» альтернативных подходов к обработке данных.

В связи с поднятыми вопросами следует вспомнить многолетнюю дискуссию Ю.И. Алимова и В.Н. Тутубалина в 70–90-е годы XX века [6–9] по вопросам применимости и адекватности теоретико-вероятностных методов в статистике.

В целом, при неудовлетворённости теоретико-вероятностным описанием погрешностей часто удобнее работать с неопределённостями и неточностями в данных с помощью методов интервального анализа. При этом вместо вероятностных распределений заданными считаются интервальные оценки результатов измерений величин, т. е. их принадлежности некоторым интервалам. В частности, в рассматриваемой нами задаче оценивания параметров линейной зависимости мы считаем, что aij e aij = [inf aij, sup aij ] и bi e bi = [inf bi, sup bi ]

(через «inf» и «sup» здесь и далее обозначены нижний и верхний концы интервала).

Пионером нового подхода к обработке данных выступил Л.В. Канторович [10]. В дальнейшем в развитие теории восстановления зависимостей с интервальными неопределённостями в данных у нас в стране значительный вклад внесли М.Л. Лидов [11], С.И. Спивак [12, 13], А.П. Вощинин [1, 14], Н.М. Оскорбин [15], С.И. Жилин [16–18], Б.Т. Поляк [19] и другие исследователи. За рубежом первой публикацией по теме стала работа Ф. Швеппе [20]. Далее значительные результаты в новом направлении были получены в работах Дж.П. Нортона,

М. Миланезе, Дж. Бельфорте, Л. Пронцато, Э. Вальтера и других (см. монографию [21] и коллективный обзор [22]). Этому же вопросу посвящены работы автора настоящей статьи [23–26], развивающие так называемый метод максимума согласования для восстановления линейных зависимостей по интервальным данным.

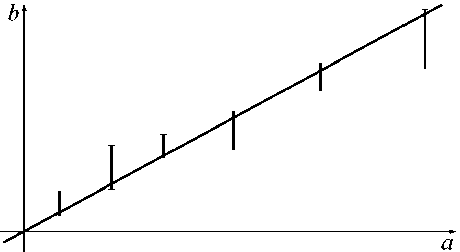
Рис. 2. Иллюстрация согласования параметров линейной модели и интервальных данных измерений, когда входные значения являются известными точно

Итак, нам необходимо найти или как-то оценить коэффициенты x i , j = 1,2,..., m , для которых линейная функция (1) «наилучшим образом» приближала бы интервальные данные. При этом идеальным является, конечно, случай, когда график восстанавливаемой зависимости проходит через все точки наблюдений, т. е. когда приближение данных в самом деле полное и имеет почти тот же смысл, что и в задаче интерполирования.

Отметим, что в постановке Л.В. Канторовича [10] и его последователей задача восстановления зависимостей по неточным данным имела не самый общий случай: неопределённости во входных данных предполагались отсутствующими, т. е. a ij = a ij . Тогда (см. рис. 2)

inf bi - ^Layxj - suP bi, j'=1

i = 1,2,..., m . Согласование параметров и данных следует понимать как прохождение регрессионной прямой через все коридоры неопределённости выходных данных. Этот случай, тем не менее, практически очень важен и именно его тщательное решение способствовало широкому распространению новых подходов на практике. При этом с математической точки зрения получаем систему линейных неравенств, которую можно решать, к примеру, методами линейного программирования.

В общем случае, когда интервальную неопределённость имеют как входные, так и выходные данные, естественным представляется следующее

Определение 1. Будем говорить, что набор параметров x1, x2,...,xn линейной зависимости (1) согласуется с интервальными экспериментальными данными ai1 , ai2 , … , ain , bi , i = 1, 2, …, m, если для каждого наблюдения i в пределах измеренных интервалов найдутся такие представители ai 1 е ai 1 , ai2 е ai2 , ... , ain е ain и bi е bi , что имеет место равенство bi = ai 1 x1 + ai2x2 + ...+ ainxn .

В соответствии с этим определением данные каждого замера входов и выхода представляют собой в пространстве R ^{n + 1} как бы большие точки, «раздувшиеся» до брусов (прямоугольных параллелепипедов с гранями, параллельными координатным осям), а прохождение графика конструируемой зависимости через такую точку понимается как её пересечение с этим брусом (см. рис. 3).

Если из интервальных данных задачи организовать m х n -матрицу A = ( a ij ) и m -вектор b = ( b _i ), то множество параметров, согласующихся с данными в смысле первого определения – это множество, определяемое как

{ x е R ⁿ | существуют такие A е A и b е b , что Ax = b } .

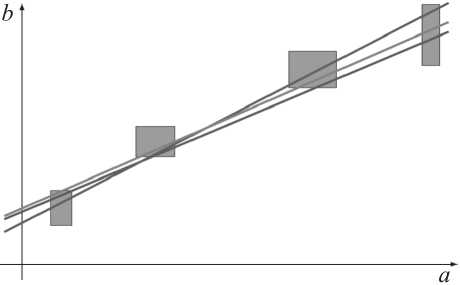
Рис. 3. Иллюстрация согласования параметров линейной модели и интервальных данных измерений

С помощью формального языка логики предикатов его можно переписать также в виде Suni(A,b) = { xe Rn | (3Ae A)(3be b)(Ax = b) }, и в интервальном анализе это множество называется объединённым множеством решений интервальной линейной системы уравнений Ax = b (нижний индекс «uni» в обозначении множества – от английского термина united solution set).

Но раздувшаяся точка-брус приобретает уже дополнительную структуру, которой не было у исходных бесконечно малых точек. Как следствие, в условиях неточности данных, когда каждое измерение-наблюдение вместо точки представляет собой целое множество возможных значений рассматриваемой величины, само понятие «прохождения через точки наблюдений» должно быть переосмыслено. Дело в том, что теперь наличие у множеств неопределённости наблюдений «тонкой структуры» вызывает необходимость различать те или иные случаи прохождения графика конструируемой функции через эти множества.

Прежде всего, нужно различать входные переменные и выходные. Входы и выходы системы (соответствующие независимым переменным функции и её значениям) отличаются друг от друга по целевому назначению, а их измерения могут выполняться отличным друг от друга способом или даже в разное время. Как следствие, различные грани бруса неопределённости замера имеют разный смысл (на рис. 3 это вертикальные и горизонтальные стороны прямоугольников), а задача восстановления зависимостей по неточным данным приобретает иной контекст. Становится важным, как именно график восстанавливаемой зависимости проходит через брус неопределённости. Если процесс измерения значений входа и выхода разорван во времени и разделён на этапы, когда выходы измеряются после фиксации значений входов, то более адекватно другое понимание «согласования» параметров и данных, при котором ограничение на выходе должно выполняться равномерно при любых значениях входов. Иными словами, действительное значение bi на выходе принадлежит bi вне зависимости от того, каковы входные значения ai1 , ai2 , … , ain в преде- лах соответствующих интервалов ai1 , ai2 , … , ain .

Формально эта ситуация описывается другим определением:

Определение 2. Будем говорить, что набор параметровx1, x2,..., xn линейной зависимости (1) сильно согласуется с интервальными экспериментальными данными ai1 , ai2 , … , ain , bi , i = 1, 2, _ , m, если для каждого наблюдения i для любых значений ai 1 e ai 1 , ai2 e ai2 , . „ , ain e ain в пределах измеренных интервалов bi на выходе найдётся такое bi e bi , что выполняется равенство b = ai 1 x1 + ai2x2 + ...+ anxn .

Множество параметров, сильно согласующихся с данными в смысле второго определения, можно описать как

^ tol ( A , b ) = { x e R n | для любой A e A найдётся такое b e b , что Ax = b } .

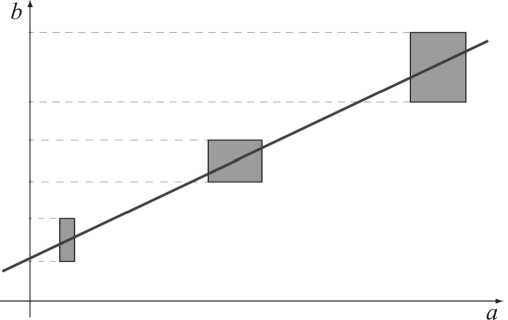
Рис. 4. Иллюстрация сильного согласования параметров линейной модели и интервальных данных измерений

На формальном языке оно определяется как

Etol(A,b) = { xg Rn | (VAg A)(3bg b)(Ax = b)} , и в интервальном анализе это множество называется допусковым множеством решений интервальной линейной системы уравнений Ax= b [27–29]. Соответствующий английский термин tolerable solution set (отсюда и индекс «tol» в обозначении множества), а точки из этого множества часто называют «tolerance solutions» [28]. Нетрудно понять, что

Etol (A, b) £ Sum (A, b), т.е. допусковое множество решений интервальной системы уравнений всегда является подмножеством объединённого.

Как и в традиционном неинтервальном случае, иногда не существует набора параметров, согласующихся с данными, т. е. линии, проходящей через все брусы неопределённости замеров в нужном нам смысле, сильном или обычном. В этом случае оценкой параметров конструируемой зависимости следует взять точку, которая обеспечивает «наименьшее несогласование» параметров и данных, аналогично тому, как это сделано в [23–26].

Итак, множество параметров модели, удовлетворяющих условию сильного согласования, является допусковым множеством решений для интервальной системы уравнений, построенной по данным наблюдений. Допусковое множество решений для интервальных систем линейных алгебраических уравнений сравнительно хорошо изучено [27–31]. Известно, что оно всегда является выпуклым полиэдральным множеством. Существуют практичные методы для распознавания пустоты или непустоты допускового множества решений, а также для его внутреннего и внешнего оценивания. В частности, можно порекомендовать читателю свободно распространяемую программу [32].

Отметим, что ранее возможность использования допускового множества решений в задаче восстановления зависимостей отмечалась в [33]. Но никаких соображений в пользу такого выбора в этой работе не представлено. Между тем в дополнение к уже сказанному о содержательных причинах применения сильного согласования и допускового множества решений можно добавить следующее. Уникальными особенностями допускового множества решений для интервальных линейных систем уравнений, коренным образом отличающими его от других множеств решений и оправдывающими введение на его основе отдельного понятия «сильной согласованности», является то, что это

• •    наиболее «устойчивое» из множеств решений,

• •    множество решений, имеющее полиномиальную сложность распознавания.

Таким образом, основанные на использовании допускового множества решений подходы к оцениванию параметров и восстановлению зависимостей будут обладать вычислительной эффективностью и, как следствие, смогут завоевать популярность у специалистов, решающих прикладные задачи. Для сравнения напомним, что распознавание и оценивание объединённого множества решений интервальных линейных систем уравнений является NP-трудной задачей. По этой причине сильная согласованность данных и параметров приводит (по крайней мере, в линейном случае) к более практичной вычислительной технологии решения задачи восстановления зависимостей, чем обычная согласованность.