Сильно гарантированное равновесие в одной иерархической двухуровневой игре при неопределенности

Постановка задачи

Рассматривается модель конфликта в виде двухуровневой иерархической игры трех лиц при неопределенности

Г = ({С ,1,2},{U,Xt }i=1,2,YUXX,{f(u,x,У)}=c,1,2), где С – игрок верхнего уровня иерархии (Центр), числа 1, 2 – порядковые номера игроков нижнего уровня. Управляющее воздействие Центра есть u е U, стратегия i-го игрока нижнего уровня есть xi е Xi, i е {1,2}. Игроки нижнего уровня независимо друг от друга выбирают свои стратегии, в результате реализуется ситуация игры (на нижнем уровне) x = (x1, x2) е X = X1 X X2. В игре Г каждый из трех игроков стремится достичь больших значений своей функции выигрыша fj (и, x, у), j е {С,1,2}. При этом он должен учитывать возможность реализации любой неопределенности y е Y .

Далее наряду с «чистыми» неопределенностями у е Y будем использовать «информирован- ные неопределенности» вида у (•): U X X ^ Y

или (в частном случае)

У(•): X ^ Y , введенные академиком Н.Н. Красовским при исследовании антагонистической минимаксной по-

зиционной дифференциальной игры [1, с. 353–354].

Перейдем к иерархической «процедуре» принятия решений в игре Г, которая заключается в определенном порядке ходов.

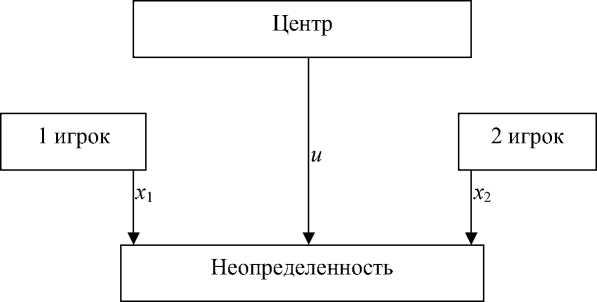
Рис. 1

Первый ход за обоими игроками нижнего уровня и Центром: они передают лицу, принимающему решения (ЛПР) и формирующему неопределенности, свои стратегии x_i е X_i ( i = 1,2), и е U (рис. 1).

Второй ход за ЛПР, анали- тически конструирующем «ин-

Математика

формированную» неопределенность, именно он определяет функцию у(•): U X X ^ Y согласно min f„ (u, x, у) = f (u, x, у (u, x)) = f [u, x] Vu e U, х e Х                      (1)

у eY c              c и передает эту функцию у(u,x) Центру (рис. 2). Здесь используем подход из работ [2-4]. Далее будем предполагать, что указанная выше функция у(u, x): U X X ^ Y существует и единственна.

Центр

1 игрок

у ( u,x )

2 игрок

Неопределенность

Рис. 2

Отметим, что согласно (1) для любой неопределенности у e Y имеет место неравенство f_c ( u , x , у ) >  f_c [ u , x ]                                             (2)

при всех ( u , x ): U X X .

Третий ход за Центром: он формирует стратегию u (•): X ^ U, u (•) e UХ , такую, что max fc (u, x, у(u,x)) = max fc[u,x] = fc[u(x),x] = fc [x] Vх e Х                  (3)

ueU                    ueU и передает эту стратегию u(•) обоим игрокам нижнего уровня иерархии (рис. 3). Здесь также предполагаем существование и единственность функции у(х): X ^ Y.

Рис. 3

Четвертый ход за игроками нижнего уровня иерархии:

во-первых, i-ый игрок (i = 1,2) строит свою вспомогательную функцию j\[x] = minf(u(x),x,у) (i = 1,2);                                (4)

уeY во-вторых, по определенной в (4) функции fi [x] каждый игрок нижнего уровня находит так называемую функцию «сожаления» по Сэвиджу [5]

Ф] [ x ] = max f [ z , x ₂ ] - f [ x , x ₂ ], z e X 1

Ф₂ [ x ] = max f [ x , z ] - f [ x , x ₂ ], z e X ₂

значения которых каждому из игроков i = 1,2 желательно получить возможно меньшими;

в-третьих , для вспомогательной бескоалиционной «игры гарантий» (без неопределенности)

Бардин А.Е.,                       Сильно гарантированное равновесие в одной иерархической

Солдатова Н.Г.                                   двухуровневой игре при неопределенности

Г G = <{1,2},{ Xi }_{fe { 1} ,2 ) ,{ ф ( X ) = Дx ] -Ф i [ x ]> _{/ е{ 1} ,2 _})

игроки нижнего уровня находят ситуацию равновесия по Нэшу [6], которая определяется равенствами max ф (х1, x 2) = ф1 (хе, x2), X1G X1

max ф 2 ( х е , x 2 ) = Ф 2 ( х е , x е ). х 2 е X 2

При этом снова будем предполагать, что ситуация равновесия по Нэшу в игре Г _G единственна.

Отметим, что равновесная стратегия х ^ е Х 1 из (6) является максимальной по Парето в двухкритериальной задаче

XX „{ f [ x , , x 2 ], -Ф 1 [ x 1 , x | ] }> , (7) тогда увеличение исхода f_x[_x 1 , x 2 ] влечет увеличение «сожаления» Ф 1 [ x 1 , x 2 ], а уменьшение «сожаления» Ф 1 [ x 1 , x2 ] приводит к уменьшению исхода f_x[_x 1 , x 2 ]. При этом значение функции

Ф 1 [ x 1 , x 2 ] в ситуации равновесия ( х 2 , x 2 ) равно нулю, что является оптимальным (наименьшим) значением этой функции на множестве X = X 1 х X ₂.

Аналогичное свойство выполняется для стратегии х 22 е Х ₂ из равновесной ситуации ( x f , x 2 ) в двухкритериальной задаче

XX 2 , { fx2 , x 2 ], -ф 2 [ xee , x 2 ] }) .                                   (8)

Раскроем «гарантированный смысл» указанного в (6) равновесия х е = ( x f , x 2 ) в исходной игре Г, именно:

с одной стороны, при известной игрокам i е {1,2} функции u (x1, x2) и любой неопределенности у е Y выполняется неравенство ft (u (x2), x2, у) > ft [ x2 ];(9)

с другой, для «замороженной» Центром u (x) и определенной равенством (1) функции у(u,x) будет f,(u (x1, x2), x1, x 2, у (u (x1, x2), x1, x 2)) < f1[ x2 ],(10)

f2( u (xe, x2), xe, x 2, у (u (xe, x2), xe, x 2)) < f2[ x2 ],(11)

для всех х ₁ е Х ₁ и х ₂ е Х ₂ .

Еще раз отметим, что minФг[x] = Фг[x2] = 0, iе{1,2},(12)

хе Х а нулевые и достигаемые в ситуации равновесия х2 значения функций сожаления являются наилучшими для каждого игрока i = 1,2.

в-ч2тв2ртых, игроки нижнего уровня «отправляют» Центру найденную равновесную (единственную) ситуацию х² е Х (рис. 4).

Рис. 4

Последний пятый ход состоит в нахождении Центром своей гарантии f c [ x² ] = f c ( u ( x² ), x² , у ( u ( x² ), x² )),

Математика

для нее выполнено неравенство j (и (xe), xe, у) > j [ Xе ] при любой неопределенности у е Y.

Определение 1. Сильно гарантированным равновесием в иерархической игре при неопределенности Г (с одним игроком верхнего уровня и двумя игроками нижнего уровня) называется набор

( X^е , и ( ■ ), jg , jg , fg ),                                       (14)

где xe = (xf, x2) - ситуация равновесия по Нэшу в игре гарантий ГG , и (■): X ^ U есть функция, передаваемая Центром игрокам нижнего уровня, величины jgg = JC [ и (xe ), xe ], j,g = f1[ xе ], fg = f2[ xе ].

При этом предполагается, во-первых, игроки верхнего и нижнего уровней, а также ЛПР, «отвечающий» за построение «информированной» неопределенности у(■), придерживаются процедуры принятия решений, описанной выше (см. ходы 1-5);

во-вторых , обе функции у ( ■ ) из равенства (1) и у ( ■ ), определенная условием (3), а также равновесие по Нэшу в игре Г _G единственны.

Очевидно следующее утверждение.

Лемма 1. Ситуация xe = ( x^ , x 2 ) будет равновесной в игре Г G тогда и только тогда, когда xe есть равновесие по Нэшу в игре

Г = ({1,2},{X („{1,},{f[x]}„(1.2|),(15)

где функции выигрыша игроков заданы равенствами (4).

Линейно-квадратичная игра без ограничений (скалярный случай)

Пусть в игре Г множества U = X1 = X2 = Y = R. Скалярные функции выигрыша игроков оп- ределены ниже: 2                         22

f Y — Л 112 4-    /7(,) У2 4- Л у2 4-3 Л^^11Х 4- 3/7 14- 3    /7(,) У jg ( и, x, у) — ^11U + у a 22 x, + азз У + 2 Т. a12 ux, + 2 a13 иу + 2 у a 23 x, у, г=1                             ,=1

j■( и, x, у) = b^1 и 2 + b22) x12 + bgg x 2 + b^g у 2 + 2 b1(2) ux1 + 2 b1(3) ux 2 + 2 b1(4) иу +

+ 2 b 23) x 1 x ₂ + 2 b 24) x 1 у + 2 b 34) x ₂ у + 2 b^ x 1 + 2 b 20 x ₂,    i e ( 1,2 } .

Из условий dfc

+ 2] Т a 2? x, = 0, i = 1

—- = 2 a ₃₃ у + 2 a ₁₃ и d у

_ a 33 >  ⁰

получаем, что min j (и, x, у) = j (и, x, у (и, x)) уeY c достигается при

у ( и , x ) = - a - 3

f)

^a 13 ^{и +} Т a 23 ^x ,

V         ,=1

Окончательно имеем fg [ и, x ] = jg (и, x, у (и, x)) = a 33

2\ц2₊ Vl/7 r,^r,^2 I y2-k ( ^a 33 ^a 11    ^a 13 ) ^{и +} y l a 33 a 22    ( a 23 ) I ^x , ⁺

,=1 V)

(^{)-Л    ( , )^У            rt^nj-j )у

+ 2T ( a33 a12   a13 a23 ) x,U 4T a23 a23 xi xj i=1

Из условий

Бардин А.Е., Солдатова Н.Г.

ɶ

^c = ² a 33 ( a 11 ^a 33 d и          ^v

2 ^a 13 ) u ⁺ 2 ( an a 33 i = 1

^a 13 a 2 *3 ) xi

= 0,

. a11a33 a13 < 0 получаем функцию и (•): X ^ U, именно и (х) = ( a23

a11 a33

)"   2 ( «& ¹ a 33

V i = 1

^ ^a 13 a 2 3 ) xi

,

которую далее пишем в виде u (х) = с1 x1 + с 2 x 2 .

С учетом последнего равенства получаем функции fV x, y ] = ft (и (x), x, y) = ( cl bn) + b22 + 2 b(2) c) x2 +(c 2 bn) + b33) + 2 bn) c 2) x 2 + 2 (с c 2 bn) + c2 bi(2) + +c1 b1(3) + b2 3) х1 х2 + b44 y 2 + 2 (b^) c1 + b24 ) x1 у + 2 (b(4) c2 + b34)) x2 у + 2 b^) x1 + 2 b20) x2, которые ниже пишем в виде f (x, y) = d11)x2 + d22x2 + 2d(2)х1 х2 + d3(3)y2 + 2d^)x1 у + 2d23)x2у + 2d 10)x1 + 2d20)x2 .(20)

Из условий dfi [x,y ] = 2 d) y + 2 d1i) x + 2 d 3 i’ x2 = 0,

]   dу d33 > 0,    i e{1,2} имеем явный вид функций гарантированных исходов для игроков нижнего уровня f [ х] = min f [ x, y] = f [ x, y^ (x)], yeY где yi(x) = h i)x1 + h2i)x2, hi) =-(d3(3)) d 1(3), h2i) =-(d33) d23), ie {1,2} .

Таким образом f [ x ] = f d((ii) + d3 i) [h; i) )2 + 2 d1i) h; i)) x2 + f d (i1 + d3(i) (h^ i) 12 + 2 d 33’ h^ i)) x 2 + 2 (d3(i) h 1 i) h 3 i) + d 1i) + d1i) h (i) + i L J 11       33 \ 1 /         13 1 11         22      33 \ 2 1          23 2 12 у 33 1 2        12      13 2

+ d 23) h ₁ ( i ) ) х ₁ х ₂ + 2 d 10 ) x ₁ + 2 d 20 x ₂,     i e { 1,2 } .

Введя новые обозначения, получаем f-[ x ] = Л71(1) x2 + k2 2 x 2 + 2 k1"2) х1 х 2 + 2 k1"0) x1 + 2 k 30) x 2.                        (23)

Используя достаточные условия существования равновесия по Нэшу в игре г=({1,2j,{ X, }i.{1.2),{Л[ x ]}i«{1.2}), решаем систему

ɶ dfL = 2 кЦ) x1 + 2 k§ x 2 + 2 k^ = 0, d^1

< -^d f ² = 2 к 22) x ₂ + 2 k^x ₁ + 2 к 20) = 0,                             (24)

^d x 2

k ff <  0,     к 22) <  0.

Равновесная ситуация xe в игре Г представима в виде xe xf =А^{- 1} А ₁,    x 2 =А^{- 1} А ₂

= ( xe , xe ), где и

A       (1)z.(2)_,(1),(2)

^ 2 = ^k 11 ^k 20 ^k 10 ^k 12 .

(1) (2)      (1) (2)                      (1) (2)      (1) (2)

^А = ^k 11 ^k 22 ^k 12 ^k 12 ^ ⁰, ^А 1 = ^k 10 ^k 22 ^k 12 ^k 20 ,

Математика

Как было отмечено выше, равновесная ситуация xe в игре Г совпадает с равновесной ситуацией в игре Г g . Суммируя полученные результаты, получаем следующее утверждение.

Теорема. Пусть в игре Г заданы множества

U = X 1 = X 2 = Y = R .

Скалярные функции выигрыша игроков определены равенствами (16) и выполнены неравенства a 33 >  0, a 11 a ₃₃ - a 2 ₃ <  0 , d ₃ (3) >  0, k i <  0, i e { 1,2 } , а также

A = kW k22) - kWk^ * 0, где величины d33), k^, ie {1,2} определены условиями (19)-(24).

Тогда в игре Г существует равновесно-сильно-гарантированное решение, явный вид которого представлен в (25).

Указанная в теореме система условий будет совместной, если, например, a 11 = a ₃₃ = a ⁽ 2) = 1, ^a i3 = V2, a 23) = 0, & i(i) = b 444) = ¹, b 22) = b 3 3) = ^{- 1}, ь^ ) = ^b i ⁽ ₃ ) =— 2, ъ^ ) = b 24) = ^b 34) = 2, ^b 2 ₃ ) = 2.

Заключение

В работе рассмотрен один из подходов к проблеме формализации риска в игровых моделях иерархических структур, который основан на принципе минимаксного сожаления по Сэвиджу. Для иерархической игры в условиях действия неконтролируемых факторов (неопределенностей) можно предложить другие способы моделирования риска игроков верхнего и нижнего уровней, используя модификации различных принципов принятия оптимальных решений из теории задач при неопределенности [2–4].